具有多传感器的CPS系统的攻击检测*
杨 康, 王 瑞,, 关 永, 李晓娟,, 施智平, Xiaoyu SONG
1(轻型工业机器人与安全验证北京市重点实验室(首都师范大学 信息工程学院),北京 100048)
2(电子系统可靠性与数理交叉学科国家国际科技合作示范型基地(首都师范大学),北京 100048)
3(Portland State University, Portland 97230, OR 97230, USA)
信息物理系统(cyber-physical system,简称CPS)在环境感知的基础上实现了计算、网络通信和物理元素的紧密结合[1].CPS改变了人们与周围物理世界的相互作用和控制方式.与传统的嵌入式系统相比,CPS具有智能化、控制精确、网络开放性等诸多优点.近年来,随着信息技术与控制技术的发展,CPS广泛应用于国家关键基础设施和工业控制等领域,包括医疗系统、供水系统、国防和武器系统等[2,3].
随着信息物理系统在安全攸关领域的应用越来越广泛,确保该系统的安全是很有必要的[4-6].因此,CPS的安全问题也越来越受到人们的重视.攻击者可能有不同的动机去恶意破坏系统,对系统造成不同程度的损坏,从性能上的轻微干扰到完全地控制系统[7].最近的工作表明,攻击者可能通过车辆的车载通信协议或传感器欺骗中的漏洞来劫持现代车辆[8,9].类似地,如Maroochy Water漏洞[10]和蠕虫Stuxnet能够通过利用监督控制和数据采集(SCADA)系统[11]中的弱点来禁用关键基础设施.
随着传感器技术的迅速发展,现代CPS通常配备有测量相同物理变量的多个传感器.例如,可以用GPS、轮编码器、超声波和IMU等传感器来测量汽车的速度.融合这些传感器的数据可以为控制器提供更准确的估计,这可能会对系统的性能和可靠性产生很大影响[12,13].即使这些传感器的精度可能不同,但是融合它们的测量不仅能够产生比任何单个传感器更精确的估计,而且还能够增加系统对外部干扰的鲁棒性[14,15].此外,具有不同精度和可靠性的不同传感器降低了系统对特定传感器的依赖性.Marzullo开发了一种融合算法,利用多个传感器的测量,产生包含真实值的融合间隔[15].在Marzullo提出的融合算法的基础上,Ivanov等人通过引入传感器传输时间表[16]和使用历史测量[17]提出了一个精确和鲁棒性的传感器融合算法.
目前已经存在许多关于传感器攻击检测问题的研究,大多数检测恶意传感器攻击的方法都主要考虑概率传感器的情况.例如,Kalman提出的卡尔曼滤波器,把假设的传感器精度和已知的系统动力学模型相结合,产生最佳线性估计[18].Kwon等人提出把卡尔曼滤波算法用于在检测测量数据是否被篡改的同时执行状态估计[19].另外,Jayasimha等人提出通过测量数据协方差矩阵中的元素的变化来检测和识别不良数据[20].然而,当系统中存在瞬态故障时,这些方法容易出现残留污染和残留淹没,将导致误报或无法检测到攻击.这些方法的特点是以相同的方式处理瞬态故障和攻击,因此忽略了传感器有时可能由于临时干扰而提供故障测量的事实.瞬态故障是指传感器在短时间内提供错误的测量并在不久之后消失.例如,在隧道中,GPS经常暂时与卫星失去连接.因此,不应该把瞬态故障看作对系统的安全威胁.为了消除这些局限性,Park等人通过为每个传感器提供一个瞬态故障模型来区分瞬态故障和攻击,并利用成对传感器关系开发了一种当存在瞬态故障时传感器攻击检测和识别的方法[21].该方法的局限性在于它们仅考虑了两个传感器不相交的情况,忽略了它们相交时也可能提供有故障测量的事实,致使有些攻击不能被检测出来.例如,隐身攻击.即,攻击者有足够的能力,为了保持不被检测到,以最大化融合间隔,并使得任意两个传感器的间隔尽可能地相交.
本文主要解决 CPS的安全问题,这通常涉及系统的最坏情况,因此,本文采用抽象传感器模型.为了解决现有的攻击检测方法存在的一些局限性,本文提出了一种基于融合间隔和历史测量的传感器攻击检测和识别方法,并考虑了两个传感器间隔相交时的故障检测问题.该方法的核心思想是从不同角度考虑传感器的测量,并为不同的传感器建立不同的故障模型,结合融合间隔和历史测量,利用两个传感器之间的不一致关系来检测攻击.此外,本文还提出了一种基于构建ROC(receiver operating characteristic)曲线来选择瞬态故障模型参数的方法.最后,本文从EV3机器人平台上获得真实的实验数据来评估算法的性能.通过获取不同窗口和攻击场景下超声波和两个大型电机的传感器数据,训练合适的瞬态故障模型,验证了本文提出的传感器攻击检测和识别方法的检测和识别性能,并分析了误报情况.实验结果表明,本文提出的方法对各种攻击类型都非常有效.特别是对于隐形攻击,本文提出的算法的优势是显而易见的,与现有的检测算法相比,检测的准确率大约提高了90%以上.
本文第 1节介绍本工作的一些基础知识,包括系统模型、传感器模型、瞬态故障模型以及攻击模型.第 2节介绍两种多传感器融合算法.第 3节详细阐述本文提出的基于融合间隔和历史测量的传感器攻击检测和识别方法,并提出一种基于构建ROC曲线选择瞬态故障模型参数的方法.为了增加算法的可读性,第3节给出一种算法的实例.第4节通过EV3平台验证算法的性能,并介绍在实际场景中瞬态故障模型的构建.第5节总结本文工作并提出未来的研究方向.
1 预备知识
为了更好地理解本文提出的基于融合间隔和历史测量的传感器攻击检测和识别方法,本节主要介绍本工作中的一些基础知识.首先介绍系统模型,并简单分析了在具有非线性系统模型的CPS中,本文提出的检测算法的可扩展性.之后介绍了本文使用的抽象传感器的模型,详细描述了传感器间隔的构建.然后介绍用来区分瞬态故障和攻击的瞬态故障模型.最后介绍本文用到的3种攻击类型:偏差攻击、随机攻击和隐身攻击.
1.1 系统模型
本文考虑具有测量相同物理变量(例如,速度)的N个传感器组成的CPS,利用多个传感器产生的冗余信息为控制器提供更准确的估计值.本文假设 CPS在T(系统运行的总时间)周期内以周期性的方式查询所有传感器,不断地获取所有传感器的测量,然后执行传感器融合算法和攻击检测算法.由于大多数CPS具有已知的动力学,本文假设CPS由一个离散线性时不变系统组成,其形式如下:
其中,xt=(xt1,xt2,xt3,...,xtn)∈Rn,表示在t时刻的状态;ut=(xt1,xt2,xt3,...,xtp)∈Rp,表示控制器在t时刻的输入信号;yt∈Rm为系统输出,即传感器的测量值;ωt∈Rq和vt∈Rl,分别表示系统干扰和测量噪声;A、B、C属于系统信息,A∈Rn×m和B∈Rn×p,分别为状态矩阵和控制输入矩阵,C∈Rm×n为输出矩阵.
本文主要研究具有上述线性系统模型的 CPS中传感器的攻击检测和识别问题.然而,本文提出的传感器攻击检测方法可以很容易地扩展到具有非线性系统模型的情况,如变速和转弯的情况.扩展思路主要有两个:(1) 根据实际的输入调整瞬态故障模型.例如,可以使用查找表,该查找表包含系统在不同操作模式下训练的多个瞬态故障模型的参数值.即,每一个速度段给出一组瞬态故障模型参数,针对不同的系统操作模式动态地选择合适的参数.(2) 针对转弯的情况.对于转弯的瞬间,那个时刻点t不使用历史测量,对于其他的时刻点,本文提出的算法都是适用的.
如图1所示,本文专注于一个广泛使用的CPS架构,它的基本工作流程是:CPS通过传感器实时地感知物理对象的变化,然后通过网络把传感器的测量信息发送给控制器.控制器中的计算单元根据多个传感器的测量信息正确地认识环境,并根据一定的算法做出相应决策,再通过网络将决策反馈给执行器,最后由执行器执行该决策,进而改变物理对象.在整个过程中,可能有些地方会受到恶意攻击.例如,在通过网络把传感器的测量发送给控制器这个过程中,攻击者可能会通过物理攻击或网络攻击篡改传感器的值,导致控制器收到的测量值是错误的,这可能导致整个CPS不能正常运行.要实现对CPS的精确控制,必须保证各种传感器输出真实可靠.因此,实现传感器故障的快速准确检测,对于提高CPS的安全可靠性具有十分重要的意义.本文结合CPS安全可靠性这一迫切需求,利用多传感器冗余信息,开展传感器攻击检测和识别方法及应用的研究.本文在控制器这里添加一种传感器攻击检测方法,当控制器收到传感器的测量值时,首先经过攻击检测算法,判断收到的值是否是正确的,然后再进行下一步工作.
1.2 传感器模型
目前文献中使用的传感器模型大致分为概率传感器模型和抽象传感器模型两类.在前者中,每个传感器向控制器提供具有已知概率分布的被噪声破坏的单个测量,如高斯分布.噪声分布对更可能成为真正有价值的点赋予更多的权重.因此,概率传感器模型非常适合分析预期的系统性能,但需要了解噪声分布的知识.其中,在错误的噪声假设条件下设计的检测器会降低攻击检测的准确性[22].在后者中,每个传感器向控制器提供一个包含所有可能为真实值的点的间隔,这种类型的传感器模型假定不知道区间上的噪声分布,但即使在最坏的情况下,也可以构造这些区间来包含未知的真实值.由于抽象测量是真实值的最坏情况界限,因此,它们非常适用于拜占庭故障和传感器攻击下系统运行的最坏情况分析.
本文采用抽象传感器模型.抽象间隔可以基于制造商关于传感器的精度和规范以及诸如采样抖动和同步误差的物理限制来构造.在本文中,每个传感器围绕其自身测量构造一个区间[Si(t)–δi,Si(t)+δi],用SiF(t) 表示.其中,Si(t)是传感器Si在t时刻的测量值,δi是传感器的误差界限(即,误差精度).传感器Si的间隔大小为2δi.间隔大小反映了传感器的精度,小的间隔意味着获得的测量具有较高的可信度.另外,传感器Si在时间t的真实值由τi(t)表示(通常是未知的).有时传感器可能会提供错误的测量,如果t时刻Si的测量值偏离真实值,并且其偏离值大于δi,则Si(t)被称为故障测量.用谓词F(Si,t)表示传感器Si在t时刻提供了错误的测量.故障测量的定义形式化为如下定义.
定义1(故障测量).
1.3 瞬态故障模型
传感器Si的瞬态故障模型是一个三元组(δi,fi,wi),其中,δi是误差界限;(fi,wi)是瞬态阈值,其指定在任何大小为wi的窗口中,Si可以提供至多fi个错误测量.瞬态阈值用于定义瞬态故障和非瞬态故障之间的边界.如果Si不违反其瞬态阈值,则称为瞬态故障,由谓词TF(Si,t)表示,否则称为非瞬态故障.
定义2(瞬态故障).
其中,如果Si在t时刻提供了故障的测量,则F′(Si,t)=1.否则,F′(Si,t)=0;如果(t≥wi),则从第 1 轮检测开始累加,即t′=1.
本文把永久性故障和恶意攻击都形式化为非瞬态故障,以相同的方式对待它们.当然,也可能存在符合瞬态故障模型的攻击,这将留作以后的工作,本文仅考虑表现为非瞬态故障的攻击.因此,如果传感器Si在整个系统操作期间至少出现1次非瞬态故障,则称Si受到了攻击,用谓词A(Si,t)表示.
定义3(攻击).
其中,T是系统运行的总时间.
1.4 攻击模型
目前,攻击者一般有物理攻击和网络攻击两种攻击手段.物理攻击是指通过损坏或替换传感器来完成,或通过其他物理手段引入偏差来实现[23].网络攻击是指通过利用其软件中的漏洞或用一个全新的版本替换其代码来危害传感器.因此,攻击者可以通过网络访问传感器,甚至不需要物理接近.在现代传感器中也可以利用在其他嵌入式系统中可能发生的任何软件缺陷.
如第 1.1节中所述,本文假设系统中的传感器通过共享总线进行通信.因此,通过获得对传感器的控制,攻击者能够获得当前轮次的所有传感器测量以及之前所有传感器发送到总线上的历史测量数据.本文假设攻击者可以代表损坏的传感器发送任何测量,并且最坏情况下攻击者具有无限的计算能力和全系统知识,包括传感器的规范、采用的传感器融合算法和攻击检测算法等.由于每个传感器的输出是一个间隔,那么,攻击者的目标是通过篡改某些传感器的值,使其间隔最大化,从而降低了所提供的测量的置信度,使系统处于不安全状态.由于CPS的性质和体系结构,攻击者可以利用物理层和网络层的弱点.根据攻击者不同的攻击目的,本文考虑3种攻击类型.
(1) 偏差攻击(bias attack).攻击者为被攻击的传感器添加一个偏差值Δ,其中,Δ=2δmax,δmax是指所有传感器中最大的误差精度.W=(w1,w2,w3,…,wT),即窗口的大小即为系统的总运行时间T.对t=1,2,…,T,有
(2) 随机攻击(random attack).该攻击类型与偏差攻击非常相似,其主要区别在于,该攻击是为t时刻被攻击的传感器添加一个随机的偏差,偏差的范围是(0,2δmax).当添加的偏差值很小时,系统很难发现此攻击.显然,随机攻击比偏差攻击更难被检测到.
(3) 隐身攻击(stealth attack).攻击者用一个新的测量代替当前时刻的测量值,最大化融合间隔的大小并尽可能地使任意两个传感器的间隔相交.这类攻击是在假设攻击者已知系统所使用的融合算法、所有测量数据以及传感器的规范等知识的前提下所设计的攻击.其攻击的目的是尽可能地保持不被检测到.该攻击类型是 3种攻击类型中危害性和隐蔽性最强的.
2 多传感器融合算法
2.1 经典的融合算法
本节介绍一种基于抽象传感器模型的融合算法,该算法由 Marzullo在 1990年提出[15].该算法的输入是N个传感器的间隔和一个数字f,其中,f表示系统中被破坏的传感器数目的上限.算法的输出是一个间隔,在本文中称为融合间隔,其跨越包含至少N-f个间隔中的最小到最大点.由于存在至多f个损坏的传感器,至少存在N-f个正确的传感器,因此真实值可以在任何N-f个间隔组中.最后,算法输出包含所有这样的组的最小间隔.
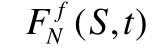
融合间隔的计算步骤如下:首先,我们对所有传感器的下界和上界分别以升序和降序进行排序,结果分别存放在str_start和str_end数组中.然后,我们按照数组下标(从0开始)从小到大的顺序开始扫描str_start,直到扫描到融合间隔的下界l与所有传感器的交点共N-f个为止,这个数值就是融合间隔的下界l.按同样的方法扫描str_end,得到融合间隔的上界h.
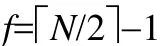
2.2 基于历史测量的改进的融合算法
在上述经典的传感器融合算法的基础上,本文提出了一种改进的传感器融合算法,其核心思想是利用历史测量来减小融合间隔的大小,从而提高融合间隔的精确度.
如第 1.1节所述,CPS具有已知的系统动力学模型,因此,可以通过系统动力学方程来使用历史测量以改进融合算法.本文将历史测量加入到融合算法中的基本思路是:把t-1时刻的所有传感器(共N个)的测量,通过动力学方程映射到t时刻,这时,t时刻就有 2N个测量值,此时发生故障的传感器的数量最大是 2f,然后使用经典的融合算法计算融合间隔.在添加过去的测量之后,改进的融合算法仍然需要满足两个标准:(1) 在包含真实值的前提下,融合间隔尽可能地小.(2) 融合间隔不大于未使用历史测量时获得的融合间隔.
为了比较上述两种融合算法,本文考虑了超声波传感器受到随机攻击的情况,分别使用两种融合算法来计算融合间隔.实验结果如图 3所示.从图中可以看出,使用历史测量的融合算法得到的融合间隔永远不会大于不使用历史测量的融合算法得到的融合间隔.该现象说明,历史测量的使用确实可以缩小融合间隔的大小,提高融合算法的精确度.
由于真实值通常是不知道的,因此很难确定哪个传感器提供了错误的测量值.Marzullo在1990年提出基于抽象传感器的融合算法的同时,也提出了一种基于融合间隔的传感器攻击检测方法.该方法的主要思想是让每个传感器与融合间隔进行比较,任何不与融合间隔相交的传感器都是故障的.
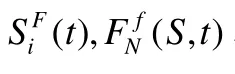
证明:在故障传感器数量有限的情况下,融合算法会产生一个包含真值的融合区间.由于真实值不可能存在于两个不相交的区间中,因此,如果传感器Si的间隔不与融合区间相交,则意味着Si一定是故障的.
3 基于融合间隔和历史测量的传感器攻击检测方法
本节描述了本文提出的用于传感器攻击检测和识别问题的改进的成对不一致(boosted pairwise inconsistency,简称 BPI)算法.该方法在基于 PI方法[21]的基础上考虑了融合间隔和历史测量,并解决了当两个传感器的间隔相交时传感器的攻击检测和识别问题.
3.1 攻击检测
本文提出的传感器攻击检测和识别方法基于传感器之间的成对不一致关系.本节首先介绍两个关键概念,即传感器之间的成对不一致类型:弱不一致性和强不一致性.该部分建立在假设真实值通常不知道的前提下,因此不知道哪些传感器提供了正确的测量.然而,已知的是传感器测量之间的相互关系,本文正是利用这种相互关联的信息来检测和识别攻击.两个传感器Si和Sj之间的第1种关系是弱不一致性,由谓词WI(Si,Sj,t)表示.如果当且仅当其中一个传感器提供了故障的测量,那么两个传感器在给定的回合中是弱不一致性的.
定义5(弱不一致性).
由于真实值是未知的,这个条件通常很难验证.因此,该定义不能用于判断两个传感器是否是弱不一致性.然而,因为真实值不能位于两者中,因此,如果两个传感器的间隔彼此不相交,则它们中的一个必须已经提供了错误的测量.
由上述弱不一致性的定义可知,瞬态故障和攻击可能在单个回合中都表现出弱不一致性.因此,本文引入强不一致性来消除两者之间的歧义.如果两个传感器中至少有一个是非瞬态故障(传感器不符合其瞬态故障模型),那么这两个传感器之间存在强不一致性.形式化地,有如下定义.
定义6(强不一致性).
与弱不一致性的定义类似,因为不知道真实值,很难判断Si是否是非瞬态故障.特别地,如果两个传感器在给定的窗口中频繁地发生弱不一致,那么它们变得强不一致.
引理1.给定传感器Si、Sj和时间t,
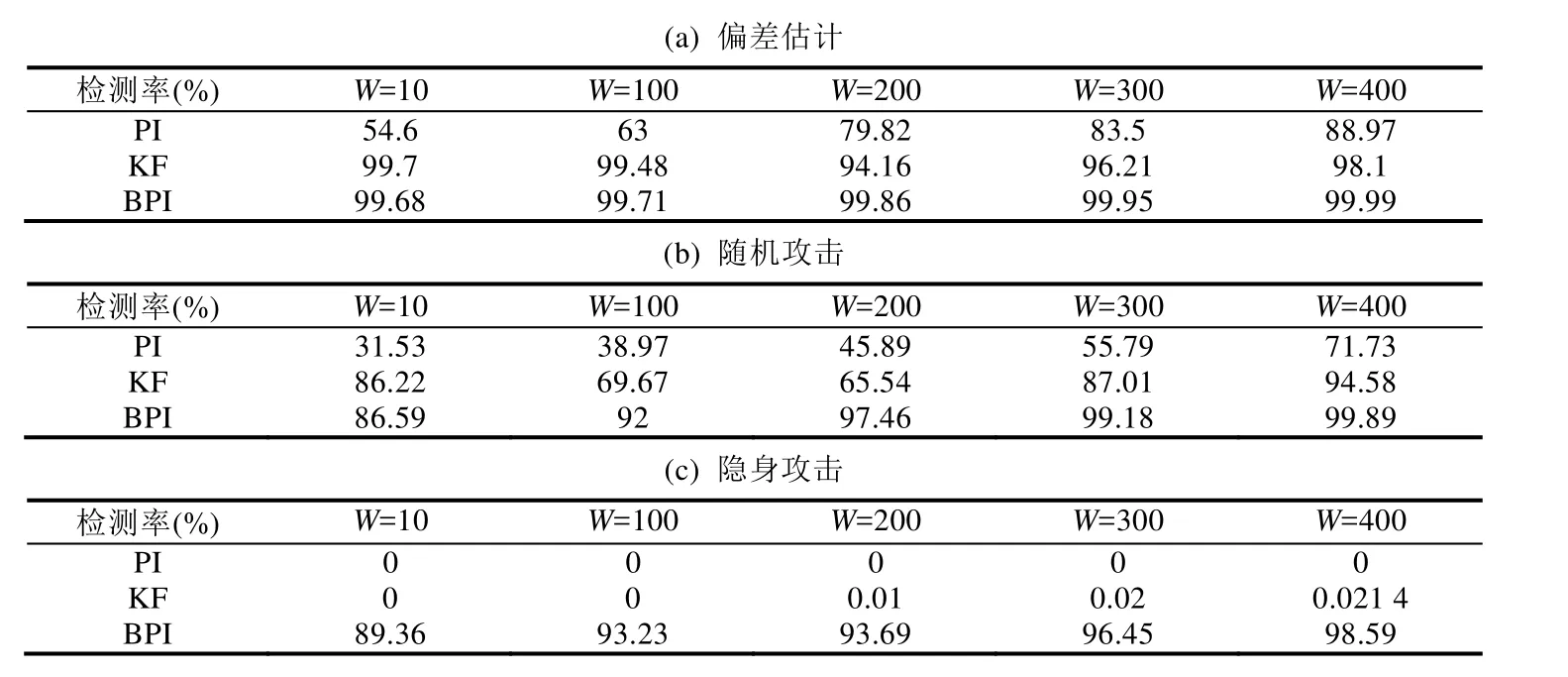
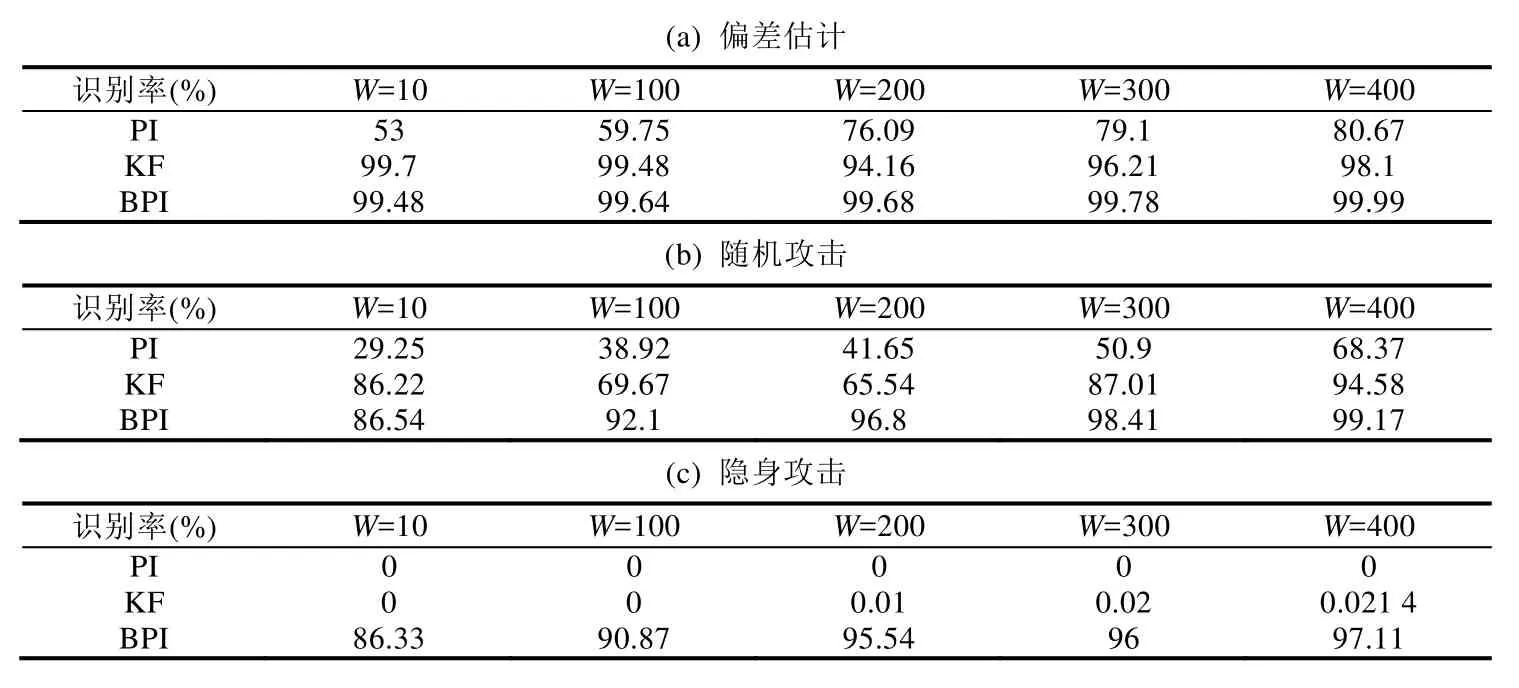
注意,如果t 3.1.1 弱不一致检测 弱不一致检测方法是本文提出的传感器攻击检测和识别方法的核心部分,是提高攻击检测和识别性能的关键步骤.由于2015年Park等人提出的基于PI的攻击检测方法仅考虑了两个传感器不相交的情况,忽略了两个传感器相交时也可能存在故障的情况,并且该方法无法检测和识别到隐身攻击.针对这些情况,本文提出了一种新的弱不一致检测方法来解决这些问题.本文提出的弱不一致检测方法分为两步. (1) 两个测量不相交. 首先比较当前时刻(t)任意两个传感器的测量,如果两个传感器的测量不相交,则至少有一个传感器提供了故障测量,即它们在t时刻是弱不一致关系. 然后融合过去和当前的测量,将所有传感器的测量从t–1时刻映射到t时刻,在t时刻共2N个测量.最后在t时刻比较任意两个测量值,注意,不包括同一个传感器不同时刻的两个测量.如果这两个测量不相交,那么这两个传感器之间存在弱不一致关系. (2) 两个测量相交. 当两个测量相交时,主要是从不同的角度利用融合间隔和历史测量来判断故障. 第1步:首先计算t时刻的融合间隔,让每个传感器和融合间隔进行比较,如果两个传感器Si和Sj均不与融合间隔相交,并且这两个传感器的测量相交,则Si和Sj是弱不一致关系. 第2步:结合历史测量进行判断.首先计算t–1时刻的融合间隔,将每个传感器在t–1时刻的测量与该融合间隔进行比较;然后把t–1时刻的测量映射到t时刻,再进行两两比较.当满足下列条件时,说明传感器Si和Sj是弱不一致关系. 算法1给出了具体实现.第1行~第8行实现了在t时刻任何两个测量之间的比较,并将不一致性信息存储在弱不一致数组中.第9行将所有传感器的测量值从时间t–1时刻映射到t时刻.第10行调用融合算法计算融合间隔.第 11行实现了当前时刻和历史的传感器测量之间的比较.第 12行完成了单个传感器和融合间隔的比较,并将这些传感器的信息存储在不一致数组中.使用弱不一致检测方法最终会得到一个弱不一致数组,里面存放了在每一个时刻存在弱不一致关系的传感器的信息.这些信息将会在传感器的攻击检测和识别中用到. 3.1.2 强不一致检测 本小节通过采用上述的不一致概念来展示本文提出的传感器攻击检测方法.由定义 6可知,如果两个传感器之间存在强不一致关系,则说明两个传感器中至少有一个是非瞬态故障.因此,由定义3攻击的定义可知,如果存在时间t≤T,使得传感器Si和Sj是强不一致的,则说明系统中存在被攻击的传感器.其中,T是系统运行的总时间. 引理2(攻击检测). 其中,如果SI(Si,Sj,t)存在,则SI′(Si,Sj,t)=1;否则,SI′(Si,Sj,t)=0. 上述的攻击检测方法仅考虑检测系统中是否存在传感器被攻击,并没有考虑哪个传感器被攻击的问题.在本小节中,为了确定哪个传感器受到攻击,本文假设系统中至多有s(s<N–1)个传感器受到攻击.本文提出的攻击识别方法是:累积强不一致信息,在强不一致对中,如果传感器Si出现的次数超过s,则称Si被攻击了. 引理3.给定传感器Si和时间t,用degree(Si,t)表示在t时刻与Si存在强不一致关系的传感器的数量. 证明:假设有n(n>s)个传感器和Si相连,与Si相连的传感器用Sj表示.由于Si和Sj是强不一致关系,如果Si没有被攻击,那么Sj必须被攻击.此时,共有n个传感器受到攻击,这与最多有s个传感器被攻击的假设相矛盾.证毕. 本文提出的 BPI方法需要精确的瞬态故障模型.现在的制造商一般会提供传感器的瞬态故障规范.尽管制造商有时候会提供算法所需要的全部参数,但对应不同的应用场景和需求,这些参数可能并不是最佳的(例如,在被高建筑物包围的环境中使用 GPS).此外,针对不同的传感器攻击算法,有些参数制造商可能无法提供,比如本文提出的BPI算法的参数fi.那么,就有必要基于经验数据来开发瞬态故障模型.因此,本节提出一种通过构建ROC曲线来选择瞬态故障模型参数的新方法,用于抽象传感器的攻击检测. 受试者工作特征曲线为ROC曲线(receiver operating characteristic curve).通常,该曲线的横轴是假阳性概率(false positive rate),纵轴是真阳性概率(true positive rate),其目的主要是用来选择最佳的界限值.将多个实验得到的ROC曲线绘制到同一个坐标中,就能很直观地看出,ROC曲线的最左上角的点表示错误率最少且准确率最高,意味着该点对应的阈值是最好的. 本文提出的选择瞬态故障模型参数方法的思想是:从实际的实验平台上获取大量的实验数据(传感器的值),把这些数据应用到攻击检测算法中(BPI方法),从而得到不同场景下传感器的攻击识别率和误报率.然后把各个场景得到的 ROC曲线绘制到同一个坐标系中.找到识别率最高、误报率最小的点,即图中最左上角的点,该点对应的参数就是最佳的参数.然而,由于每个参数对应的值可能有无数多个,不可能把每一个参数的每个值都进行实验来得到其对应的识别率和误报率.因此,在进行实验之前,需要筛选出这些参数可能的取值范围,然后再取这些范围内的点进行实验,最终确定参数的取值.在第1.3节中提出的瞬态故障模型有3个参数.参数δi使用制造商提供的值,另外两个参数fi和wi使用本文提出的基于构建 ROC曲线选择参数的方法进行确定.其基本步骤如下. (1) 初步筛选参数,选择若干个值作为fi的候选值.根据受到攻击的传感器数量,本文考虑 3种攻击情况:只有一个传感器受到攻击,另外两个传感器没有故障;一个传感器受到攻击,另外两个传感器仅有一个传感器存在瞬时故障;一个传感器受到攻击,另外两个传感器均存在瞬时故障.通过对无攻击无故障的传感器数据添加上面 3种攻击和故障,会得到一些训练数据.此外,分别用fi–1和fi+1代替3种类型的攻击中的fi来形成一系列新的训练集.通过实验得到不同fi对应的识别率和误报率.最后,本文选择几个误报率较小但识别率还能接受的fi作为候选值.这样做虽然不能保证攻击检测率最大,但可以保证误报率最小. (2) 根据第 1.4节中设计的攻击模型,为原始数据(无攻击、无故障的传感器数据)添加 3种类型的攻击.针对(1)中选取的每个候选值进行实验,获得对应窗口的误报率和识别率后,构建 ROC曲线,然后确定最终的参数值.本文选取参数的具体细节将在第4.1节中加以详细介绍. 本小节主要是想通过一个简单的例子来进一步解释上述传感器攻击检测和识别算法.为了便于解释,本文使用一个不一致图G(V,E)来描述该算法.在不一致图中,每个传感器对应一个顶点,两个顶点之间的关系代表它们之间的不一致关系.如果该关系是弱不一致关系,则该图表示弱不一致图,用WI_Graph表示;如果该关系是强不一致关系,则该图表示强不一致图,用SI_Graph表示.该不一致图的定义如下. 定义7(不一致图). 本文设计了如图4所示的实例,图中有4个传感器,窗口W=5,垂直虚线表示真实值(未知).假设系统中传感器S1和S4受到攻击(最多有2个传感器被攻击).注意,不要求被攻击的传感器在每一轮次中均受损,但需要满足在给定窗口中是非瞬态故障,每个传感器的瞬态故障模型见表1. Table 1 The parameters of the transient fault model in the example of Fig.4表1 图4实例中对应的瞬态故障模型的参数 根据第3.1.1节介绍的弱不一致检测算法,得到如WI_Graph所示的弱不一致关系图.从图中可以看出,系统在每一轮次中都检测到了弱不一致对.在t=1时,传感器S1和S2之间存在弱不一致关系,这意味着这两个传感器至少有一个提供了错误的测量.到t=3为止,S1和S2之间共出现了3次弱不一致关系.根据第3.1.2节介绍的强不一致检测方法可知,S1和S2之间存在强不一致关系,这意味着系统中存在攻击,其他类似.该实例中所有传感器的强不一致关系如图 4中的SI_Graph所示.SI_Graph中的虚线代表在之前的检测中已经出现过该强不一致对.虽然,在t=3时,检测到系统中存在攻击,但此时无法判断哪个传感器受到了攻击.直到t=5时,发现传感器S1和S4的度均为3,大于2,根据第3.2节中给出的攻击识别算法可以识别出在t=5时S1和S4均受到了攻击. 本节从EV3机器人平台上获取实际的实验数据来评估BPI算法的性能.首先介绍实验的基本设置,之后介绍瞬态故障模型的参数选择问题,然后评估几种算法的攻击检测和识别性能,最后分析误报的原因. 本文的实验平台选择 LEGO EV3地面车辆,如图 5所示.EV3是 2013年 LEGO公司开发的第三代MINDSTORMS机器人.它可以安装多个传感器,包括超声波、电机(内嵌角度传感器)、陀螺仪、颜色传感器等.根据需求,本文使用2个大型电机和1个超声波传感器来测量EV3的速度.这3个传感器均可提供10Hz的测量. 为了获得鲁棒的瞬态故障模型参数,本文根据第 3.3节提出的参数选择方法选择最终的实验参数.具体是,根据制造商提供的测量误差设置传感器的瞬态故障模型的参数δi.对某个确定的窗口wi,通过真实的训练数据来确定fi的值.本文首先以0.7m/s的恒定速度驱动EV3机器人直线运动,每个传感器收集400个测量数据.利用第 3.3节提出的参数选择方法进行实验,为了模拟真实的攻击情形,窗口wi中每个传感器提供的故障数是随机的.根据实验结果,本文建立了如图6所示的ROC曲线来确定fi的值.ROC曲线的x轴表示误报率(误报的数量/识别的总数量),y轴表示识别率((识别的总数-误报的总数)/测试总数).为了避免混淆,图6中不包括w400的情况.从图中可以看出,左上角的数据点具有更高的识别率、更低的误报率,该点对应的fi是最佳阈值.表 2总结了可变窗口大小的故障模型参数,其中,wi表示窗口大小为i的检测器. Table 2 Fault models for the sensors on EV3表2 EV3上瞬态故障模型的参数 为了评估本文在第3节中介绍的BPI算法,本节首先在平坦的地面上以恒定的速度驱动EV3来收集每个传感器的数据.本文收集了20次来自EV3设备上的未被攻击的传感器数据,其中,所有传感器以10Hz平均采样40s,因此,每个传感器有400个测量值. 本文假设在固定窗口中,攻击者对3个抽象传感器中的1个进行攻击,具体哪一个传感器被攻击是未知的.同时,对于被攻击的传感器,本文添加第1.4节中设计的3种攻击类型.注意,被攻击的传感器不要求在每一轮中都提供故障的测量,每个窗口中传感器提供故障测量的数量是随机的,但需要保证在给定窗口中是非瞬态故障.此外,在所有的检测数据中,其他传感器可能存在瞬态故障,也可能不存在瞬态故障.表3给出了不同窗口和攻击场景下3种攻击检测和识别方法的检测率.其中,KF方法是一种基于卡尔曼滤波器的传感器攻击检测方法.从表中可以看出,本文提出的BPI算法能够比已有的算法检测到更多的攻击.对于3种攻击,BPI方法在任何窗口中都比PI和KF方法更加鲁棒,并且随着窗口大小的增加,BPI方法逐渐达到稳态检测率.对于偏差攻击,KF方法与BPI的检测性能相近,BPI检测器的平均检测率比PI检测器大约高25%,比KF方法高约2%.然而,对于随机攻击,KF方法的检测性能明显低于BPI方法,小窗口中BPI检测器比PI检测器平均约高53%,在大窗口中约高35%,平均比KF方法高14%.特别地,对于隐身攻击来说,BPI方法的优势是显而易见的.现有方法的检测率几乎是0,而BPI方法能够检测到攻击,其检测率平均能达到90%以上.PI方法不能检测到隐形攻击,是因为隐身攻击的特点就是尽可能地最大化融合间隔并使当前时刻任意两个传感器之间的间隔尽可能地相交.而 PI方法恰好是基于两个传感器之间的间隔不相交来判断故障的,所以,基于PI的方法无法检测到这种攻击.基于KF的方法在大的窗口中偶尔可以检测到攻击,但检测率仅有 0.01%左右.并且,其误报率很高,这将在下一小节中详细加以介绍. Table 3 Detection rate表3 检测率 本文提出的 BPI算法的识别性能与检测性能几乎相同,但是识别比检测需要花费更长的时间.表 4显示了不同窗口和攻击情形下 3种传感器攻击检测方法的识别率.这些结果表明,对于偏差攻击和随机攻击,除了 KF方法外,其他两种方法的识别率通常随窗口大小而有所改善.从表 4(a)可以看出,对于偏差攻击,BPI方法的识别率大约平均比PI方法高30%左右,仅比基于卡尔曼的方法高3.3%左右.对于随机攻击来说,BPI方法大约平均比PI方法高49%左右,比基于KF的方法约高14%左右.从表4(b)可以看出,基于KF的方法对于随机攻击的识别性能明显降低.这是由于,随机攻击为被攻击的传感器在被攻击的时刻随机添加一个 0~0.7的一个偏差值,当这个偏差值较小时,由于测量值和估计值的偏差比较小,就会导致 KF方法无法检测到故障.特别地,从表 4(c)中可以看出,对于隐身攻击,基于PI的方法的识别率为0,基于KF的方法的识别率在大的窗口中偶尔能够检测到1次攻击,仅0.01%左右,并且其误报非常高.然而,本文提出的BPI方法平均可达到93%. Table 4 Identification rate表4 识别率 表5总结了不同窗口大小中 3种方法的误报率.实验结果表明,3种方法都存在误报,这可能是由于这些窗口中存在瞬态故障的原因.此外,我们注意到,BPI方法的误报率略高于PI方法.主要原因是瞬态故障的存在不能保证每轮被损坏的传感器数量不超过f,即无法保证融合间隔一定包含真实值.此外,由于使用传感器历史测量,在某些攻击情形中可能由于从根据历史测量预测的当前测量不够准确,导致误报增加.然而,从表中可以看出,KF方法的误报率非常高.其出现误报的原因主要是由于瞬态故障的存在,导致KF方法产生残留污染和残余淹没,从而造成误报.此外,需要注意的是,对于偏差攻击和随机攻击,KF方法的误报率与BPI相近,但对于隐身攻击,其误报率能达到50%以上. Table 5 False rate表5 误报率 本文研究了在存在瞬态故障时CPS的安全问题.首先在Marzullo提出的经典融合算法的基础上,通过融入历史测量提出了一种改进的融合算法,该算法可以得到更精确的融合间隔,具有更强的鲁棒性.此外,本文结合历史测量和融合间隔提出了一种新颖的传感器攻击检测和识别方法,用于具有测量相同物理变量的多个传感器的CPS.并且,提出了一种基于构建ROC曲线的方法来选择瞬态故障模型.最后在EV3平台上获得实际的实验数据,验证了算法的性能,并与现有的基于卡尔曼滤波器的方法和基于 PI的方法进行了比较.实验结果表明,该算法在各种攻击场景下均优于现有的算法.基于本文的评估,未来的工作包括尝试使用形式化验证方法来验证所提出算法的正确性,并将该算法部署在实际系统上进行工业实践.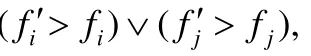
3.2 攻击识别
3.3 瞬态故障模型参数选择
3.4 传感器攻击检测实例

4 实验评估
4.1 实验设置

4.2 检测性能分析
4.3 识别性能分析
4.4 误报分析

5 总 结

