经编间隔织物的缓压性能
陈美玉, 孙润军, 张长琦, 刘先锋
(1. 西安工程大学 纺织科学与工程学院, 陕西 西安 710048; 2. 中国军事科学院 军需工程技术研究所, 北京 100190)
经编间隔织物由于具有间隔丝构成的独特结构特征使其具有良好的压缩形变能力和回弹性能[1],能够有效缓解人体压力和吸收冲击能量。同时该材料与纤维絮料及海绵等相比,具有良好的透气性能[2],可作为手术台布[3]和医用护理垫[4],或用作老年人防止摔伤的膝部防护材料[5-6]。特别是经编间隔织物的良好支撑性能和卓越的缓压功能,使得该材料在汽车坐垫[7-9]、枕头[10]、床垫[11]、文胸罩杯[12]等垫用材料方面备受青睐。
作为垫用材料,间隔织物设计的目的是确保材料具有一定支撑性能的同时,尽可能改善其缓压性能。垫用材料受到人体头部或身体的载荷作用而被压缩时,人体同时受到材料的支撑,材料能够将人体感受的压力进行有效分散,确保人体感到舒适而没有受压迫的感觉,即具有缓压效应,因此,经编间隔织物的缓压性能是消费者以及生产厂家极为关注的热点。目前,国内外部分学者对经编间隔织物的缓压性能已做了初步的研究。包括经编间隔织物的压力分散原理分析,利用医用接触传感系统或足部传感器测试证明经编间隔织物确实具有优越的缓压性能,并分析研究了间隔织物缓解压力的影响因素[13-14]。通过对间隔织物球面压缩与人体坐姿臀部压强分布进行实验研究发现:压缩深度和压头半径与体感压力舒适性呈正相关,与平均压强呈负相关;人体舒适性与压强峰值、压强均值等密切相关[15]。并可通过对经编间隔织物的缓压性能进行主、客观评价分析,将主观分类和客观聚类进行对比发现二者具有很好的一致性,研究表明压力峰值、单位质量的平均减压量及平均梯度积分可有效地评估间隔织物的减压效果[16-18]。此外,借用聚氨酯软泡材料行业中常用的压陷硬度指标测试分析经编间隔织物的压陷性能,也可间接地表征间隔织物的缓压性能[19]。
设计经编间隔织物必须系统地研究间隔织物的缓压性能与其结构参数之间具体的量化关系。本文基于人体受力部位与经编间隔织物作用时所受压强,从理论上分析经编间隔织物压缩过程中的缓压性能与其结构参数之间的关系,并采用球形压缩模拟人体凸起部位受力,研究分析间隔织物的缓压性能与主要结构参数之间的关系,旨在为经编间隔织物的缓压性能设计提供一定的理论参考。
1 经编间隔织物的缓压机制
经编间隔织物的缓压性能是针对人体感受而言的,是人体与间隔织物相互作用的结果。由于人体呈曲线状,无论是坐或躺的时候,人体重力作用分布在垫用材料表面都是非均匀的,在凸出部位如臀部,往往会产生应力集中,人体感觉受压严重。经编间隔织物之所以产生舒适感是因为当人体作用于间隔织物时,间隔织物会产生较大的形变,经编间隔织物的压缩位移量越大,该间隔织物与人体曲线吻合越好,受力面积增大,人体坐或躺在经编间隔织物时压力便能进行最大程度地分散,致使人体没有被压迫而产生舒适感。因此,经编间隔织物的缓压性能实质就是人体所感受压强的大小。人体感受的压强越小,间隔织物的缓压性能就越好。
1.1 人体与经编间隔织物作用的压缩载荷
人体的臀部等凸起部位的实际形状是不规则的球体,为使理论分析简单可行,假设它是半径为R的圆球体。当压缩载荷为F0的圆球体对经编间隔织物进行压缩时,间隔织物会发生形变,如图1所示。

图1 经编间隔织物受圆球体压缩示意图
Fig.1 Schematic diagram of warp-knitted spacer fabric compressed by spherical ball
由图1看出,间隔织物形变部分包括接触区和非接触2部分。当球体向下移动时,球体首先需要克服接触区的间隔丝形变而产生的力。其次,还需要克服由于间隔织物面层的整体效应产生的一个斜向上的拉力F′。假设F′与水平成夹角β,则有:
F0=F′cosβ+F
(1)
式中:F0为圆球体的压缩载荷,N;F′为间隔织物面层的整体效应产生的一个斜向上的拉力,N;β为F′与水平方向的夹角,(°);F为接触区间隔丝发生形变产生的力,是压缩过程中接触区各间隔丝形变而产生的力之和,N。假设接触区有n根间隔丝,每根间隔丝最初均呈圆弧状,且忽略接触区间隔丝之间的摩擦力,由文献[20]可得:
(2)
式中:E为间隔丝的拉伸模量,N/mm2;d0为间隔丝圆形截面的直径,mm;R为间隔丝的原始状态的曲率半径,mm;α为间隔丝的垫纱角度,(°);l为间隔丝的喂入长度,mm;r1、r2、ri分别为压缩过程中接触区第1、2、i根间隔丝的曲率半径,mm。接触区每根间隔丝的曲率半径取决于单丝的形变,是由其在球体的位置决定的。间隔丝越靠近球体的底部,形变越大,其因压缩形变而产生的反作用力越大。
将式(2)代入式(1)得:
(3)
1.2 人体感受的压强
当经编间隔织物受到人体压缩时,人体受到的压强P为
(4)
式中:F0为压缩载荷,N;S为人体与经编间隔织物接触区的面积,m2。
由图1可以看出,圆球体(人体)与经编间隔织物接触区的面积S实际上就是底部半径为r,球冠高度为h2的圆球球冠ACB的表面积,如图2所示。球冠ACB可以看成是球冠面积微分单元dS积分所得,假设∠AOD=θ,则
dS=2πrR·dθ
(5)
又r=Rcosθ
(6)
将式(6)代入式(5)得
dS=2πR2cosθ·dθ
(7)
则球冠表面积S计算如下:
(8)
由图2可以得到:
h2=R-Rsinθ=R(1-sinθ)
(9)
将式(9)代入式(8)得球冠的表面积
S=2πRh2
(10)

图2 球冠示意图
Fig.2 Schematic diagram of a spherical crown
将式(3)、(10)代入式(4)中,可得圆球体作用于经编间隔织物时受压压强
(11)
事实上,经编间隔织物在受到球形压缩时,间隔织物与球体的接触区及非接触区的临界接触点A、B的位置受球体的半径、间隔织物的软硬度以及间隔织物面层的延伸性能等诸多因素影响[20-21];但考虑到人体臀部的曲率较小,即当圆球体的半径足够大时,非接触区的面积所占的比例会非常小,因此,为使理论计算切实可行,此处忽略非接触区的影响,则圆球体在压缩过程中的压缩位移h1就等于圆球体与间隔织物接触的球冠高度h2,且间隔织物的斜向上的拉力F′也可忽略,即有:
(12)
由此可见,当间隔丝的材质确定时,人体与经编间隔织物作用时所感受的压强主要取决于间隔织物的三大因素:1)间隔丝直径d0;2)接触区间隔丝的根数n,其取决于间隔丝单位面积内的排列根数,本文定义为间隔丝的排列密度;3)间隔丝的喂入长度l和原始曲率半径R,其最终取决于间隔织物的厚度H0。此外,垫纱角度α也有一定的影响。
2 实验部分
2.1 实验样品及测试仪器
本文选用33.33 tex(96 f)的涤纶弹力丝作为面层和底层,不同直径的圆形截面涤纶单丝作为间隔丝原料,通过拉舍尔双针床经编机制备经编间隔织物样品,样品的实测主要结构参数如表1所示。其中间隔丝的排列密度为将间隔织物试样剪成20 mm×20 mm后,计算其所包含的间隔丝的根数,然后换算成每平方厘米的根数。实验样品尺寸为20 cm×20 cm。测试前,试样在温度为(27±2) ℃,相对湿度为(65±5) %的测试环境中放置24 h。
测试仪器采用深圳三思纵横的UTM4304型电子万能试验机。为模拟人体凸起部位受力情况,对电子万能试验机的上压头进行自行设计,改造成球形压头,其示意图如图3所示。为使实验结果更接近于理论分析,球形压头半径R设计综合考虑到人体臀部的曲率以及测试样品的尺寸和特性等因素,最终设计值为81.25 mm。
表1 经编间隔织物样品的主要结构参数
Tab.1 Main structural parameters of warp-knittedspacer fabric samples
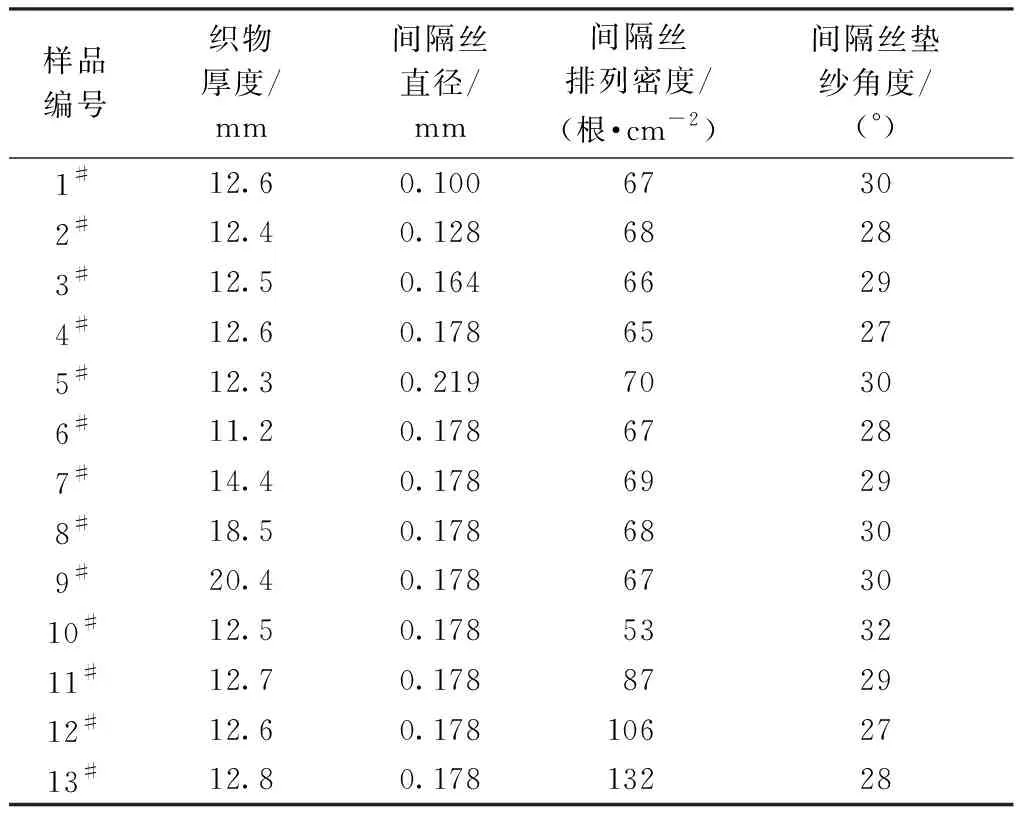
样品编号织物厚度/mm间隔丝直径/mm间隔丝排列密度/(根·cm-2)间隔丝垫纱角度/(°)1#12.60.10067302#12.40.12868283#12.50.16466294#12.60.17865275#12.30.21970306#11.20.17867287#14.40.17869298#18.50.17868309#20.40.178673010#12.50.178533211#12.70.178872912#12.60.1781062713#12.80.17813228
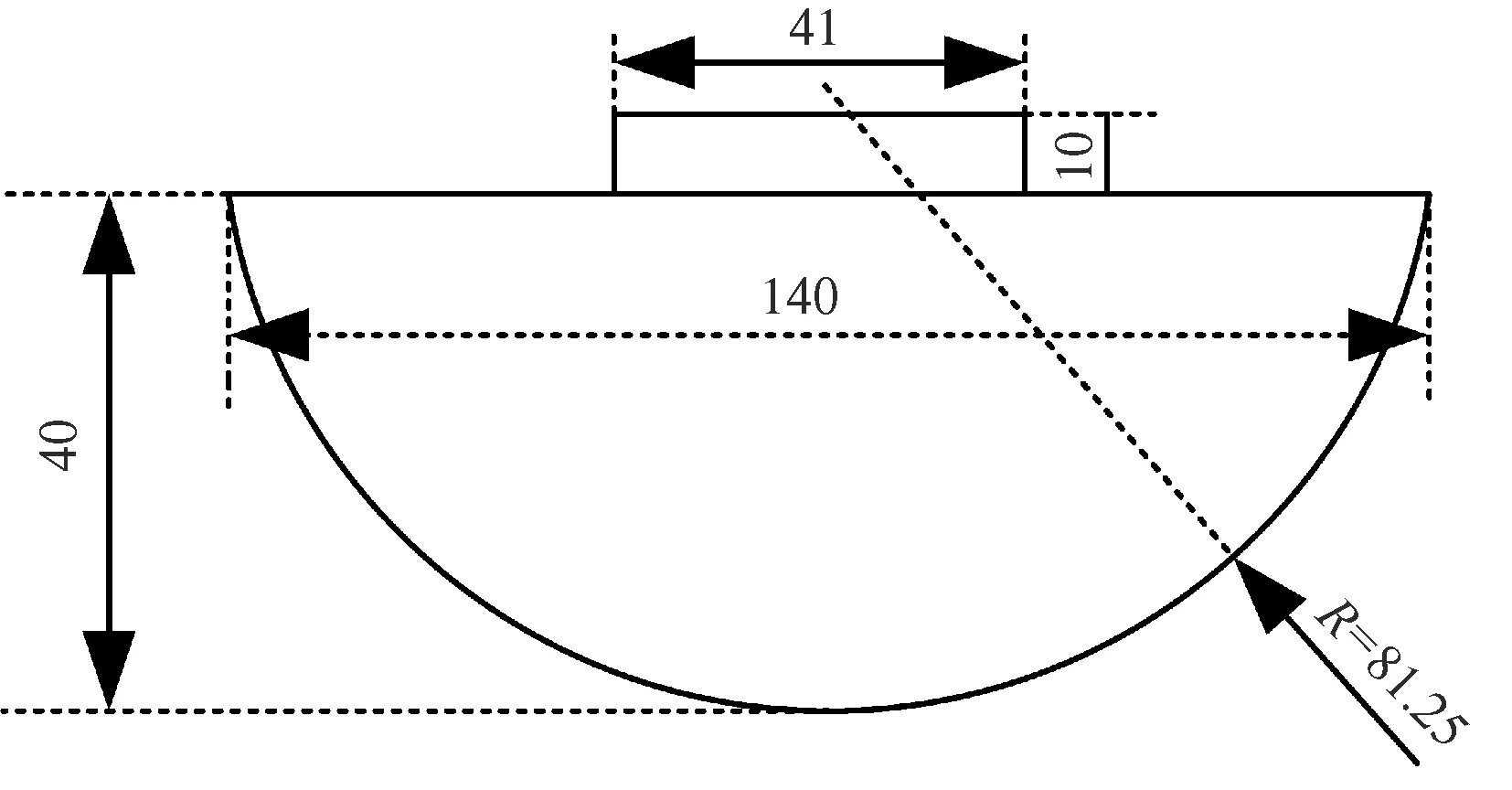
注:图中数值单位为mm。 图3 设计的球形压头示意图
Fig.3 Schematic diagram of designed spherical indenter
为防止间隔织物受压时在压板上滑移,用双面胶把经编间隔织物试样固定在万能材料试验机下压板上。测试时,将三思万能电子试验机的上压板换成半径R为81.25 mm的球形压头,对所有样品进行球形压缩实验。根据压缩实验结果,综合考虑各种间隔织物的承载能力,选定压缩载荷为30 N时对应各样品的球体压强,分析样品的缓压性能与其主要结构参数之间的关系。
2.2 实验结果与分析
2.2.1 间隔丝直径对缓压性能的影响
图4示出压缩载荷为30 N时间隔丝直径对间隔织物的缓压性能的影响。可以看出:当样品的厚度、间隔丝的排列密度和垫纱角度基本相同时,随着间隔丝直径的增加,球体所受的压强迅速增加。在载荷为30 N下,对不同间隔丝直径的经编间隔织物样品进行压缩时,5#样品球体所受的压强达52.08 kPa,然而1#样品球体所受的压强下降近90%,只有5.30 kPa。很显然,此时人体与1#样品作用时缓压效果是最好的。究其原因在于间隔丝可看成一个弹性体,直径越粗,其弯曲力矩越大,在相同载荷作用时间隔丝的形变就越小[22]。即球体的压缩位移就越小,从而受力面积也就越小,所以球体所受的压强就越大。

图4 间隔丝直径对经编间隔织物缓压性能的影响
Fig.4 Influence of spacer filament diameter on pressure reduction property of warp-knitted spacer fabrics
从理论分析得知,可对实验数据采用幂函数进行回归,得到球体所受的压强与间隔丝直径之间的回归方程:
(13)
式中:P为球体所受压强,kPa;d0为间隔丝的半径,mm;γ为相关系数。通过与理论方程对比看出,间隔丝的半径与球体所受压强确实呈幂函数关系,且理论分析与实验结果具有较好的一致性。
2.2.2 间隔织物厚度对缓压性能的影响
图5示出压缩载荷为30 N时间隔织物的厚度对其缓压性能的影响。结果表明:当样品的间隔丝直径相同,间隔丝排列密度和垫纱角度基本相同时,随着经编间隔织物厚度的增加,球体所受的压强随之下降。6#样品球体所受的压强达22.15 kPa,然而9#样品球体所受的压强只有10.48 kPa。可见,相同压缩载荷时,9#样品的缓压性能更优。且随着经编间隔织物厚度的增加,球体所受压强下降的速度刚开始较快,但随着间隔织物厚度的进一步增加,其下降的速度会逐渐放缓,并最终会趋于一个定值。产生这一现象的原因可能是:间隔织物中间隔丝相当于一个弹性杆件,间隔织物的厚度增加,意味着喂入的间隔丝的长度增加,当间隔丝的垫纱角度相同时,外加的压缩载荷使得间隔丝杆件更容易失稳而形变,因此压缩位移有所增加,所以球体所受的压强会减小。需要说明的是,当间隔丝的材质和直径确定时,间隔织物厚度的变化只能在一定的范围内,才能使所设计的间隔织物同时具有一定的支撑性能和缓压效果。
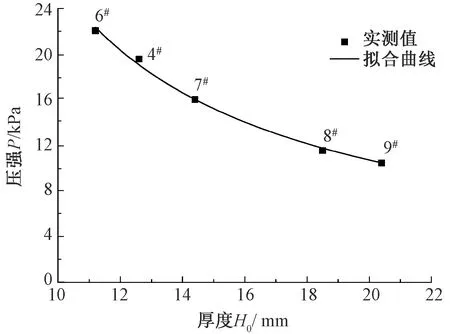
图5 间隔织物厚度对经编间隔 织物缓压性能的影响
Fig.5 Influence of spacer fabric thickness on pressure reduction property of warp-knitted spacer fabrics
上述分析表明可采用反比函数对实验结果进行回归,得到球体所受的压强与间隔织物厚度之间的回归方程:
(14)
式中,H0为间隔织物的厚度,mm。由回归系数γ看出,实验结果与理论回归具有很好的一致性。
2.2.3 间隔丝排列密度对缓压性能的影响
图6示出压缩载荷为30 N时间隔丝排列密度对其缓压性能的影响。可以看出:当样品的间隔丝直径相同、织物厚度和间隔丝垫纱角度基本相同时,随着间隔丝排列密度的增加,球体所受的压强也随之增加,即织物的缓压性能下降。10#样品的间隔丝排列密度为53根/cm2,球体所受的压强达17.80 kPa,然而13#样品的间隔丝排列密度增加为132根/cm2,球体所受的压强增加到27.3 kPa,所以该样品的缓压性能略差。产生这一现象的原因很简单,根据前面的理论分析可知:间隔丝排列密度增大意味着间隔织物的支撑杆件数增加,这样间隔织物的形变能力会减弱,所以当相同的压缩载荷作用时,球体与间隔织物接触区的面积就会下降,进而球体所受的压强会增加。需要特别说明的是:当间隔丝排列密度增加至一定程度时,30 N的压缩载荷作用可能会使间隔织物几乎不发生形变,此时球体所受的压强理论上应该是无穷大,但实际过程并非如此,因人体自身会发生一定的形变,即此时人体所受的压强会趋于一个定值。
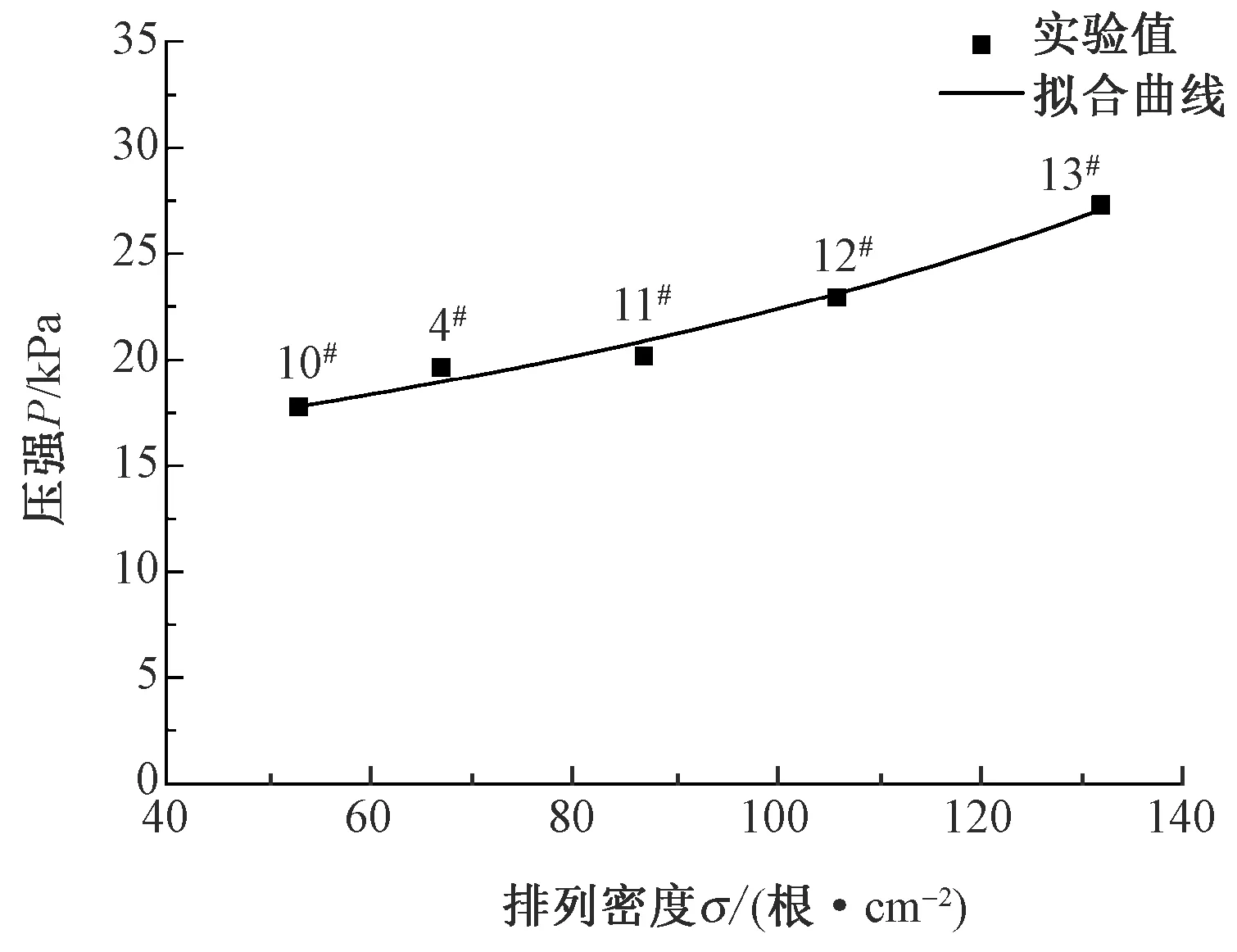
图6 间隔丝排列密度对经编间隔织物 缓压性能的影响
Fig.6 Influence of arrangement density of spacer filaments on pressure reduction property of warp-knitted spacer fabrics
根据球体所受压强的上述变化趋势,对实验数据进行理论回归,可得球体所受的压强与间隔织物中间隔丝的排列密度之间的回归方程:
(15)
式中:σ为间隔织物中间隔丝的排列密度,根/cm2。由回归系数γ看出,在本文实验范围内实验结果与理论回归具有很好的一致性。
3 结束语
经编间隔织物的缓压性能实质就是人体感受的压强大小。人体感受的压强越小,间隔织物的缓压性能就越好。本文基于人体受力部位与经编间隔织物作用时所受压强,从理论上分析经编间隔织物压缩过程中的缓压性能与其结构参数之间的关系,并采用球形压缩实验验证分析间隔织物的缓压性能与主要结构参数之间的关系,得出了各自的理论回归方程。研究结果表明:间隔织物压缩过程中人体所受压强与间隔丝直径呈幂函数变化,与织物的厚度和间隔丝排列密度分别呈反比和正比函数关系。
此外,本文以压缩载荷30 N为例,研究经编间隔织物缓压性能与其主要结构参数之间的关系。研究发现,不同的压缩载荷作用下,间隔织物缓压性能的变化趋势基本相同,但回归方程中的参数可能会有所不同。

