“三重门”模式探究机车启动问题
广西
在新课标人教版高一物理必修2第七章第二节《功率》中,关于机车启动问题,无论在新课还是高三复习课,都是每一位物理教师不可回避的内容。功率中有关机车启动模型,作为变加速模型的经典案例之一,在高考中也会时不时出现,两类启动问题既是中学物理中的重点和难点,也是中学物理分析宏观运动问题的重要案例。从力和运动上看,既是匀变速直线运动、变加速直线运动的延伸和拓展,也是牛顿运动定律的进一步运用和分析。同时,还需要综合考查掌握平衡问题、功率问题、能量守恒问题、动能定理、各种运动物理量图象分析等等。清晰地分析和掌握机车启动问题,是培养学生物理核心素养的重要途径,是培养核心素养中“相互作用力观、能量观”的方面之一。
显然,高一新生欲在短时间内完全理解是不现实的,往往需要通过分析例子,逐步提高能力才能得以实现。近日,笔者通过一节公开课后进行教学反思,要理解和掌握机车启动问题需要突破“三重门”来实现,“三重门”就是逐步实现从简单到复杂的三个过程。在此,笔者是想通过分析探讨引起同行们对机车启动问题的思考和讨论,达到抛砖引玉的作用。
一、“一重门”—情景模型的构建与规律分析
模型的构建是中学物理核心素养的重要方面,两类机车启动问题是中学物理的基本规律,构建物理情景是高一新生必须要培养的核心素养。模型的构建是不能一步到位的,总是从简单到复杂逐步建立起来的,教材的安排是在直线运动和曲线运动之后探讨机车启动问题,非常符合学生的认知规律。
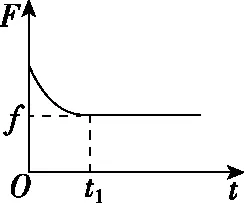
1.以恒定(额定)功率启动
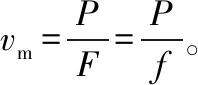
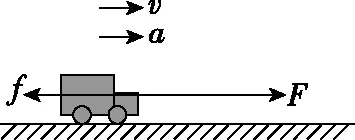
图1

图2
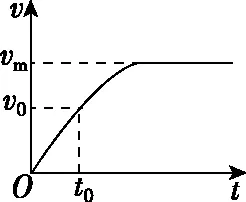
2.以恒定加速度(或牵引力)启动
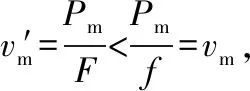

图3
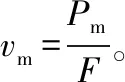
3.实例分析
【例1】一列火车总质量M=500 t,机车发动机的额定功率P=6×105W,在轨道上行驶时,轨道对列车的阻力f是车重的0.01,求:
(1)火车在水平轨道上行驶的最大速度;
(2)在水平轨道上,发动机以额定功率P工作,当行驶速度为v1=1 m/s和v2=10 m/s时,列车的瞬时加速度a1、a2各是多少;
(3)在水平轨道上以36 km/h速度匀速行驶时,发动机的实际功率P′;
(4)若火车从静止开始,保持0.5 m/s2的加速度做匀加速运动,这一过程维持的最长时间。
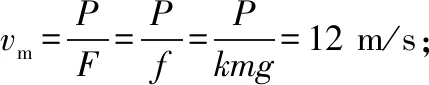
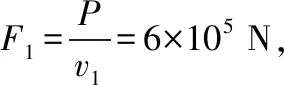
(3)当列车匀速运动,则发动机的实际功率P′=fv=5×105W;
【小结】以上分析的是常规的教学内容和“一重门”的基本要求,这是目前大多数教师和资料复习过程中的基本形式,通过掌握常规的基本问题,达到基本应用和解题能力。我们在“一重门”阶段,还是属于构建阶段,例题和难度还不能太大,例题和题型也应言简意赅,当然,也可以从水平方向受力转变为竖直方向受力进行讨论机车启动问题。
二、“二重门”—多维度思考分析与拓展应用
1.应用几种物理量图象分析
关于“二重门”,是指对知识的维度进行发散的理解分析,也是物理核心素养中从学生“已有水平”到学生“学会水平”的过程,让学生通过已有的物理模型和规律,通过科学论证和再论证的进一步分析,实现培养和发展学生物理核心素养的课程目标。
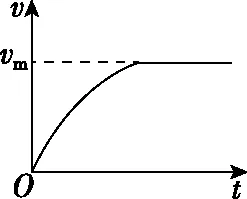
例如,在分析两类问题过程中,让学生试图通过几种图象方法分析过程。笔者在教学过程中发现,图象问题是十分锻炼学生素养的,如图5、6所示分别为两类机车启动问题中机车的输出功率P、牵引力F、加速度a、速度v与时间t的图象关系。显然,机车启动的方式不同,运动的规律就不同,即其功率、速度、加速度、牵引力等物理量的变化规律不相同,分析图象时应注意坐标轴的意义及图象变化所描述的规律。在教学过程中,这样做的目的是能让学生在掌握“一重门”的基础上,跨入“二重门”,实现自我消化和拓展应用。
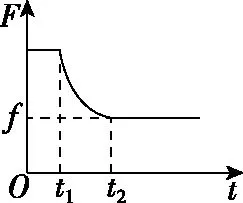
2.应用能量转化关系分析过程
多维度思考是我们理解物理过程全面而有效的方式,分析机车启动问题时应在掌握基本规律的基础上从图象、能量、斜面、电磁感应等更复杂的受力运动情景分析、审视机车启动问题,这样才能使思维跨越“二重门”。
【例2】在一次抗洪抢险活动中,解放军某部利用直升机抢救一重要落水物体,静止在空中直升机上的电动机通过悬绳将物体从离飞机90 m处的洪水中吊到机舱里。已知物体的质量为80 kg,吊绳的拉力不能超过1 200 N,电动机的最大输出功率为12 kW,为尽快把物体安全救起,操作人员采取的办法是:先让吊绳以最大的拉力工作一段时间,达到最大功率后电动机就会以最大功率工作,当物体到达机舱时恰好达到最大速度。(g取10 m/s2)求:
(1)落水物体刚到达机舱时的速度;
(2)这一过程所用的时间。
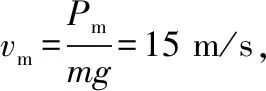
【小结】关于变力做功,不能用做功的定义式来求解,因为机车以恒定功率运行时,牵引力是变力,做功可以用W=Pt,由动能定理Pt-Fx=ΔEk求解,此式经常用于求解机车以恒定功率启动过程的位移或速度。
在解决机车启动问题时,首先要弄清是哪种启动方式,然后采用分段处理法,运用牛顿第二定律、运动学公式或能量守恒定律等知识来求解,也可以利用各个物理量图象和情景分析运动过程,分析各物理量的变化及相互制约关系,准确找出临界点,从而进一步解答出结果。
三、“三重门”—自洽性原理分析与学科观
1.关于自洽性
自洽,简单地说就是若按照自身的逻辑推演,可以证明自身至少不是矛盾或者错误的,这就是自洽性。根据物理的学科特点,在研究物理学科过程中本身就需遵循自洽性,如果在学科内出现不自洽的情况,说明在论证过程中理论本身出现矛盾或者理论依据出现问题。
汽车以恒定功率启动时做加速度逐渐减小的加速运动,当加速度减为零时,速度达到最大,高中阶段的常见解法是根据功率公式和动能定理求解,但是通过仔细分析,我们发现有不少教辅资料的习题在编写数据或者在利用模型分析时,出现一些结果、结论不自洽性。例如,在教学中,笔者遇到一个例子。
【例3】一列火车质量是1 000 t,由静止开始以额定功率沿平直轨道向某一方向运动,经1 min前进900 m时达到最大速度,设火车所受阻力恒定为车重的0.05,(g取10 m/s2)求:
(1)火车行驶的最大速度;
(2)火车的额定功率。
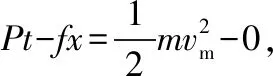
(2)火车的额定功率为Pm=kmgvm=1.5×107W。
【错误解析】(部分学生)我们还看到一部分学生的下面这种解法:
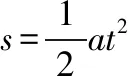
这两种解法的结果完全一样,但是第二种解法是匀变速直线运动的规律。难道匀变速直线运动的规律也适用于恒定功率启动吗?问题出现在哪里?
2.理论推导
机车保持恒定功率P从静止加速运动,根据受力有
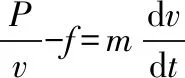
方程为微分方程,可用分离变量求解
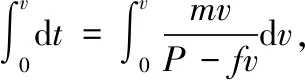
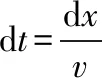
把P和m、f带入上式,得出时间和瞬时速度关系为
当速度等于30 m/s时,时间趋向于无穷大,也就说明恒定功率启动下的火车最大速度永远无法达到30 m/s,只能无限接近它,如图7所示,通过分析,恒定功率的瞬时速度与功率、运动时间都是相互制约的,如果草率设置命题条件,就会产生命题给的条件自相矛盾,出现不自洽性,让学生对知识出现困惑、怀疑。当然,要完全解释清楚上面的矛盾,显然已经超出中学阶段要求,笔者通过阅读相关文献,也可以从多方面论证和讨论。实际上,中学阶段讨论机车启动问题是理想的,是忽略次要因素而展开讨论的,阻力恒定的条件设置本属于理想运动状态。
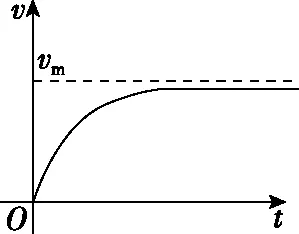
图7
我们虽然往往认为趋于匀速就是最终处于匀速状态,严格来说这个是不严谨的,甚至是错误的,按理论模型分析,车永远在做加速度越来越小的加速运动,匀速状态永远达不到,图象中的最大速度只能是条渐近线。在机车启动的理论模型中,如果以恒定功率做加速运动,则永远不能达到最大值。在一些高考试题中,也曾出现过一些题目不自洽情况,如下例题。
【例4】(2014年重庆卷)某车以相同功率在不同的水平路面上行驶,受到的阻力分别为车重的k1和k2倍,最大速率分别为v1和v2,则
( )
A.v2=k1v1B.v2=k2v1

【解析】该题的求解思路是牵引力小于阻力时,机车不断加速,而机车功率保持不变,即功率恒定,牵引力不断减小,直到减小到等于阻力,此时速度达到最大。这里的分析看似很合理,可是由精确理论可知,此加速过程在有限时间内是达不到最大速度的,只是无限接近最大速度。题设中同时出现恒定功率运动、最大速度及求解速度间的关系,其严谨性和自洽性需要进一步考虑。
3.正确的物理学科观
根据新课程理念,物理教学应尽可能回归生活、回归社会。教师在物理教学过程中能结合实际生活探讨机车启动问题,是对功率一节的升华,是动力学与能量学的一个结合点,是实现核心素养培养的重要载体。机车启动问题是重要的知识部分,同时能很好地锻炼学生各种能力,特别是核心素养中的科学思维。当然,中学阶段是以理想状态和模型为主,很多问题和解释需要到大学才能深入探讨,我们每一位物理教师都可以鼓励和引导一些学有余力的同学向物理学科观这方面去探讨,甚至去查阅相关资料,激发学生兴趣,为他们以后进入大学深造起到促进作用。
四、结束语


