连续参数型动力吸振器吸振效果分析*
贾富淳,孟宪皆
(山东理工大学 交通与车辆工程学院,淄博 255000)
机械振动是机械设备运转过程中一种常见的现象,有害的机械振动会降低机械设备运转的性能和精度,甚至会造成设备的疲劳破环,因此,关于振动控制的问题一直是国内外学者研究的热点。
动力吸振器又称调谐质量阻尼器,其基本原理为:在主系统上附加一个子系统,适当调节该子系统的结构参数和安装位置使得主系统振动的能量发生转移,从而达到振动控制的目的。由于具有结构简单、安装方便等优点,动力吸振器已广泛的应用于土木工程、航空航天和车辆公程等学科领域,成为振动控制的重要手段[1-2]。
动力吸振器按照其结构形式可以分为离散参数型动力吸振器和连续参数型动力吸振器[3]。离散参数型动力吸振器结构简单且易于实施,但较窄的抑振带宽导致其使用有很大局限,为了提高离散型动力吸振器的性能,国内外学者提出了各种结构形式与工作方式的动力吸振器,其中,三要素型动力吸振器[4]采用弹簧与阻尼串联,再与另一弹簧并联的形式,具有比常规动力吸振器更好的吸振效果;多个动力吸振器并联或者串联可以形成组合式动力吸振器,在质量比不变的条件下,组合式动力吸振器具有更好的减振效果,文献[5-7]对此做了深入的研究,并应用于土木工程结构振动控制中。1968年J.C.Snowdon的《阻尼机械系统中的振动》[8]出版,标志着动力吸振器的研究由离散参数型向连续参数型转变,连续参数型动力吸振器的模态丰富,可以同时对多自由度离散系统和连续系统的多个模态振动进行控制。文献[9]采用中间固定的双向悬臂梁作为吸振器控制单自由度系统的振动,分别采用能量法和模态近似法对耦合系统进行分析,得到了最优的质量比和阻尼比。文献[10]利用功率流的方法研究了悬臂梁吸振器对薄板振动的控制效果,并分析梁的结构参数、梁在板上的连接位置对吸振效果的影响,分析结果表明悬臂梁动力吸振器具有良好的吸振效果和吸振带宽,且梁的安装位置对吸振效果的影响较大。文献[11]以功率流为基础,结合有限元的方法,分析了连续参数型动力吸振器的吸振效果,且通过ANSYS软件的优化模块,对连续参数型的动力吸振器进行了优化设计,提升了其吸振效果。
针对连续参数型动力吸振器相比离散参数型动力吸振器所具有的优点,本文提出一种用于控制杆纵振的连续参数型动力吸振器,通过模态综合的方法,将动力吸振器两个模态同时调整到主系统对应的固有频率上,从而实现同时对杆的两阶模态振动进行控制。
1 动力学建模
杆-动力吸振器混合振动模型如图1所示,其中,纵向振动的杆左端为惯性载荷F,质量为M,右端为弹性载荷,刚度为k,杆轴向位置为x,在时间为t时的纵向变形为U(x,t),E1,ρ1,A1,l1分别为杆的弹性模量、密度、横截面积和长度;在杆轴向位置x=a处附加连续参数型悬臂梁动力吸振器,其中,在杆横向位置y处相对于杆的横向变形为W(y,t),E2,ρ2,A2,l2,I分别为动力吸振器的弹性模量、密度、横截面积、长度和截面惯性矩。

图1 杆-动力吸振器混合振动模型Fig.1 Hybrid vibration model of a rod - dynamic vibration absorber
1.1 杆纵振的模态分析
取杆的微元做受力分析,可以得到杆做纵向振动的运动方程[12]为
(1)
c2=E1/ρ1
(2)
由式(1)可以得出杆纵向变形U(x,t)的形式解:
U(x,t)=φ(x)q(t)
(3)
(4)
q(t)=Csinω1t+Dcosω1t
(5)
式中:A,B,C和D为由边界条件确定的常数;φ(x),q(t)为杆的振型函数;ω1为频率。
由弹性载荷和惯性载荷的边界条件可得
(6)
(7)
将式(3)、式(4)和式(5)代入式(6)和式(7)可得
(8)
由式(8)可得出杆纵向振动的各阶固有频率ω1(i),由于A1,A2的取值并不影响杆的振动形态,所以将ω1(i)代入式(4)即可得到第i阶模态振型函数φi(x)的精确解。
由杆模态振型关于质量的正交性可得

(i≠j)
(9)
关于刚度的正交性可得

(i≠j)
(10)
各阶模态质量为
(11)
各阶模态刚度为
(12)
1.2 动力吸阵器横向振动的模态分析
对于连续参数型动力吸振器,假设其做纯弯曲且不考虑弯曲时消耗的能量,取悬臂梁的一个微元做受力分析,可以得到动力吸振器做横向振动的运动方程为
(13)
由式(13)可以得到动力吸振器横向振动的形式解:
W(y,t)=Y(y)F(t)
(14)
Y(y)=C1sinβy+C2cosβy+C3sinhβy+
C4coshβy
(15)
F(t)=C5sinω2t+C6cosω2t
(16)
式中:Y(y),F(t)为W(y,t)的振型函数;C1~C6均为系数,由边界条件确定;ω2为动力吸振器的固有频率;β为位置系数,且
(17)
对于悬臂梁连续参数型动力吸振器,其上端为自由端,下端为固定端,因此,动力吸振器的边界条件为
由第一组边界条件可得
C2=-C4,C1=-C3
由另外三组边界联立可以得到关于C3和C4的代数方程组:
(18)
C3,C4有非零解的条件为
(19)
式(19)与式(17)联立,可以求出连续参数型动力吸振器的各阶固有频率ω2(j),确定C3和C4的比值ξj为
其中βj为悬臂梁j阶振型函数的位置系数。
由于常数C4的大小不影响振动形态,所以令C4=1,则可以求出悬臂梁j阶振型函数为
Yj(y)=coshβjy-cosβjy+ξj(sinhβjy-
sinβjy)
(20)
由悬臂梁模态振型关于质量的正交性可得
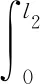
(21)
关于刚度的正交性为
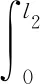
(22)
可以得到各阶模态下的模态质量为
(23)
模态刚度为
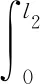
(24)
1.3 混合振动系统运动微分方程的建立
杆左端所受的纵向集中力为F(t),是频率为ω的简谐力。假设该简谐力激起杆第i阶振动模态和连续参数型动力吸振器的第j阶振动模态。
耦合动力吸振器后全系统的动能为
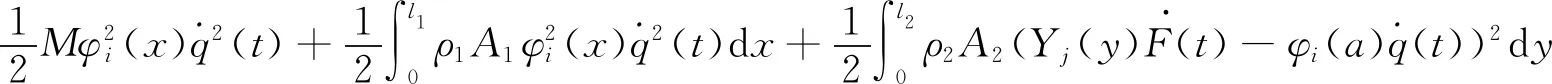
(25)
全系统的势能为
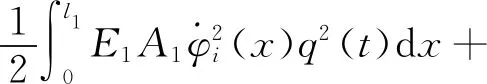
(26)
将式(11)、式(12)、式(23)、式(24)代入式(25)、式(26)可得
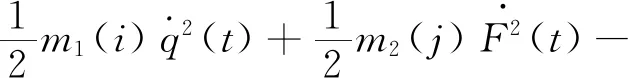
利用拉格朗日方法得到系统的运动微分方程,写为矩阵的形式:
(27)
式中:m1(i)为模态质量;k1(i)为模态刚度。
将式(27)进行拉普拉斯变换后,可以得到广义传递函数H(ω),ω为频域频率,对其进行无量纲化,可得
(28)
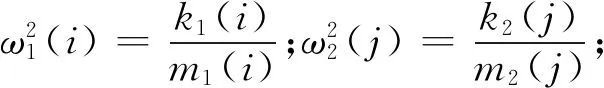
则杆的纵向变形为
U(x,t)=F(t)φ(0)H(ω)φ(x)
(29)
进一步推导可以得到杆传到基础上的力与激励力的力传递率为
A(g)=kH(ω)φi(l1)φi(0)
(30)
可知力传递率为频率比g、固有频率比f、质量比μ和动力吸振器的线密度ml2的函数,当ω=ω2(j)时,1-f2/g2=0,力传递率为零值,即若连续参数型动力吸振器的各阶固有频率均等于激励频率,则杆的稳态振动消失。通过对悬臂梁型动力吸振器的参数进行调整使得吸振器的各阶固有频率与杆纵振的固有频率相等,可以使杆的各阶模态振动消失,即悬臂梁连续参数型动力吸振器的设计需要满足的条件为
ω1(i)=ω2(j)
(31)
2 动力吸振器的设计
取杆的材料为铸钢,其计算参数如下:密度ρ1=7 800 kg·m-3,弹性模量E1=1.75×1011Pa,长度l1=10 m,惯性质量M=1 000 kg,刚度k=1×109N·m-1,横截面积A1=0.19 m2。根据式(8),得到一个一元超越方程,采用最小二乘法得到其数值解,解即为杆纵振的各阶固有圆频率。采用连续型动力吸振器控制杆前两阶模态振动,只给出两阶固有圆频率:
ω1(1)=241.43 rad·s-1,
ω1(2)=1 445 rad·s-1
采用等截面圆柱合金钢作为连续参数型悬臂梁动力吸振器,其计算参数如下:密度ρ2=7 900 kg·m-3,弹性模量E2=2.06×1011Pa,直径D=0.1 m,动力吸振器在杆上的安装位置为a=1 m。根据式(31),使ω1(1)=ω2(1),计算可以得到动力吸振器的长度l2=1.36 m;使ω1(2)=ω2(2),计算可得l2=1.39 m,由于对一二阶模态振动控制的权重相同,因此,确定悬臂梁动力吸振器的长度为l2=1.375 m。
3 吸振效果的分析
由式(28)可知,对于杆-动力吸振器的耦合系统,若只考虑某一阶模态下悬臂梁动力吸振器的吸振效果,则该问题相当于单自由度离散动力吸振器的吸振效果分析问题。
分别截取杆-动力吸振器耦合振动系统的一阶和二阶模态进行分析,计算各阶的模态质量和模态刚度,对于第一阶模态,f=0.98,μ=7.08×10-5,ml2=62.31 kg·m-1;对于第二阶模态,f=1.02,μ=4.3×10-4,ml2=63.52 kg·m-1。相应的力传递率A(g)如图2和图3所示,由图2和图3可知,附加连续参数型动力吸振器后,原来的一阶二阶模态振动消失;a和b为耦合动力吸振器前后力传递率A(g)曲线的交点,当频率比g位于a,b两点之间时,对连续参数型动力吸振器的影响是有利的,则当外界激励频率的范围位于220~265 rad·s-1和1 416~1 517 rad·s-1时,连续参数型动力吸振器可有效控制杆的纵向振动。
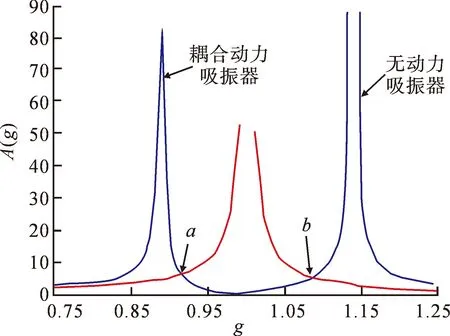
图2 一阶模态吸振效果分析Fig.2 Effect of the first order mode shock absorption
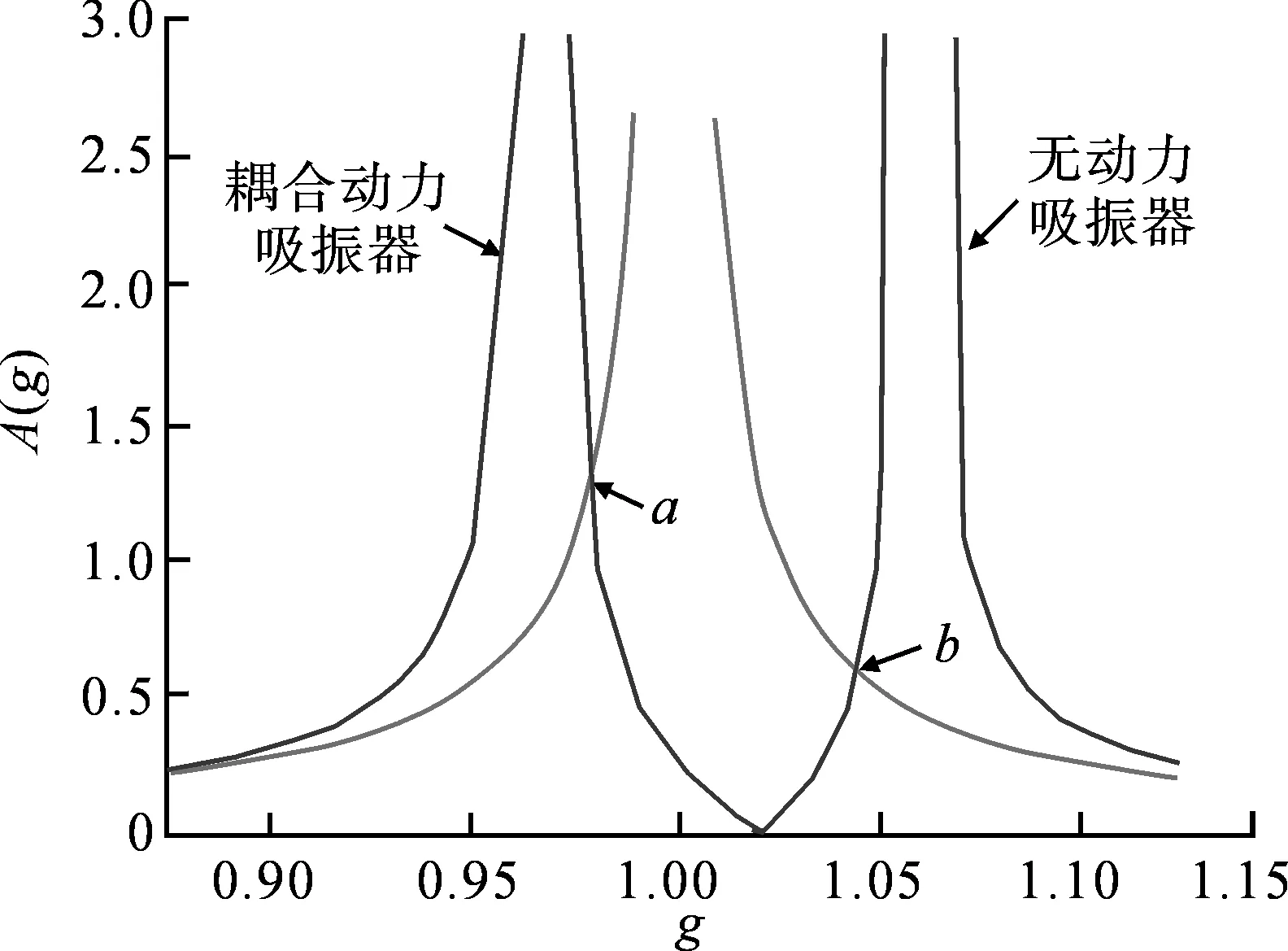
图3 二阶模态吸振效果分析Fig.3 Effect of the second order modal shock absorption
4 安装位置对吸振效果的影响
讨论一阶模态下,连续参数型动力吸振器不同的安装位置a对吸振效果的影响,分别取a=1 m、5 m和10 m,即动力吸振器分别位于杆的前端、中段和尾部时,分析其吸振效果,得到力传递率A(g)如图4所示。
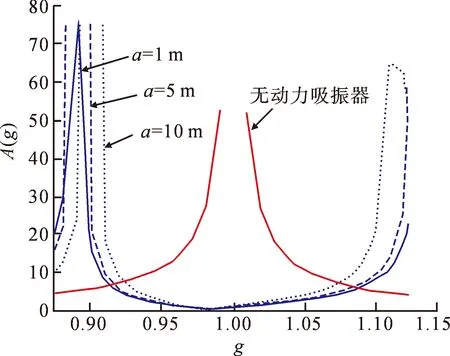
图4 一阶模态不同安装位置对吸振效果的影响Fig.4 The effect of different mounting positions on the vibration absorption of the first-order mode
由图4可知,吸振器的安装位置对吸振器的有效吸振带宽有较大影响,随着a的增大,共振频率附近的两个峰值向中间移动,导致有效的吸振带宽减小。因此,应使连续参数型悬臂梁动力吸振器安装到杆的前端,从而获得更大的有效吸振带宽。
5 结 论
1)采用模态综合的方法,调整吸振器的振动模态,使其与杆的固有频率相等,实现了同时控制多阶模态振动,得到了在特定边界条件下,杆纵向振动与梁弯曲振动固有频率的解析表达式和振型函数的解析表达式。
2)在广义坐标下,基于杆-动力吸振器混合系统的运动微分方程,得出了杆传到基础上的力与激励力的力传递率的无量纲表达式。
3)提出了一种用于控制杆纵向振动的连续参数型悬臂梁动力吸振器,连续参数型悬臂梁动力吸振器可以同时控制杆的两阶模态振动,给出了可以有效吸振的频率范围。
4)吸振器的安装位置对有效吸振带宽有较大的影响,将吸振器布置于杆的前端可使连续参数型动力吸振器获得更大的吸振带宽。

