空间曲线桥弹塑性传递关系研究*
杨 帆,凤 涛,谢 衍,刘永辉
(1.西安工业大学 建筑工程学院,西安 710021;2.中国铁路西安局集团有限公司,西安 710054)
传递矩阵法起源于20世纪,旨在解决弹性力学问题,基本思想是将一个整体结构视作多输入多输出的线性系统,系统若干单元或子结构的输出载荷与输入载荷之间力学特性的分析转化为若干单元或子结构对接矩阵与传递矩阵的力学分析,基于矩阵乘法对结构进行静力学特性、动力学特性以及稳定性的分析[1-2]。结构的固有频率和主振型可通过力学矩阵进行解算,反映了系统的硬度、质量、形状和材质,矩阵形式有助于建模和分析元件组成的系统所处的各种条件和相应作用。
传递矩阵法能够解决曲线梁的各种内力分析问题,辅助体系传递矩阵法是一种借助辅助体系来求解矩阵的精确解法[3],文献[4]在考虑剪切变形条件下基于辅助体系法对空间直线梁桥传递关系进行了建模分析。与有限元分析法相比,传递矩阵方法模型精度高,计算误差较小,利于编程计算,本文采用辅助体系法对空间曲线梁的弹塑性进行建模和分析,进而推导了塑性铰的不同模型传递关系。
1 曲线梁的分析模型
曲线梁桥的应用非常广泛,其力学分析极为重要。曲线梁在外荷载作用下会产生弯-扭耦合效应,产生弯矩的同时也会产生扭矩,产生竖向挠曲变形的同时也会产生扭转角,由于这种耦合效应,其变形值要比一般直线桥大[4-8]。
曲线梁的空间分析模型为
S=[NxQyQzMxMyMzuvwθxθyθz]T
式中:Nx为轴力;Qy,Qz为剪力;Mx,My,Mz为弯矩;x为切向坐标;y为径向坐标;z为竖向坐标;u为x向位移;v为y向位移;w为z向位移;θx为x向转角;θy为y向转角;θz为z向转角。
此模型包含12个状态量。
2 曲线梁弹塑铰模型分析原理
根据曲线梁的受力及变形特点,塑性铰模型可分为塑性铰弯曲模型、塑性铰剪切模型、塑性铰扭转模型以及塑性铰拉压模型[9-12]。
2.1 塑性铰弯曲模型
分析模型采用转角模型(如图1所示),Ml为杆左端弯矩,Mr为杆右端弯矩,l为杆左端,r为杆右端。在杆件单元的两端设置等效弹簧来表示杆件单元的弹塑性变形,任意恢复力模型来表达杆件的刚度[10]。
杆件的转角关系可以表示为
(1)
式中:θl为杆左端转角;θr为杆右端转角;θ′l为左端弹性转角;θ′r为右端弹性转角;αl为左端塑性转角;αr为右端塑性转角。当αl和αr为0时,杆件处于弹性变形的状态。
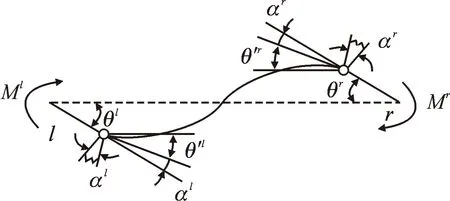
图1 模型转角图Fig.1 The corner of the model
结构塑形变形建模采用杆端弯矩M与杆端转角θ的恢复力模型。图2(a)为弯矩和总转角的关系,图2(b)为弯矩与塑性转角的关系[10]。p1为弯矩与转角的关系中超过弹性阶段刚度的比例系数;f1为弯矩与塑性转角的关系中超过弹性阶段刚度的比例系数;k1为弹性阶段的刚度;θ′为弹性扭转角;α为塑性扭转角;Δα为塑性扭转角增量;My为扭矩的极限值。
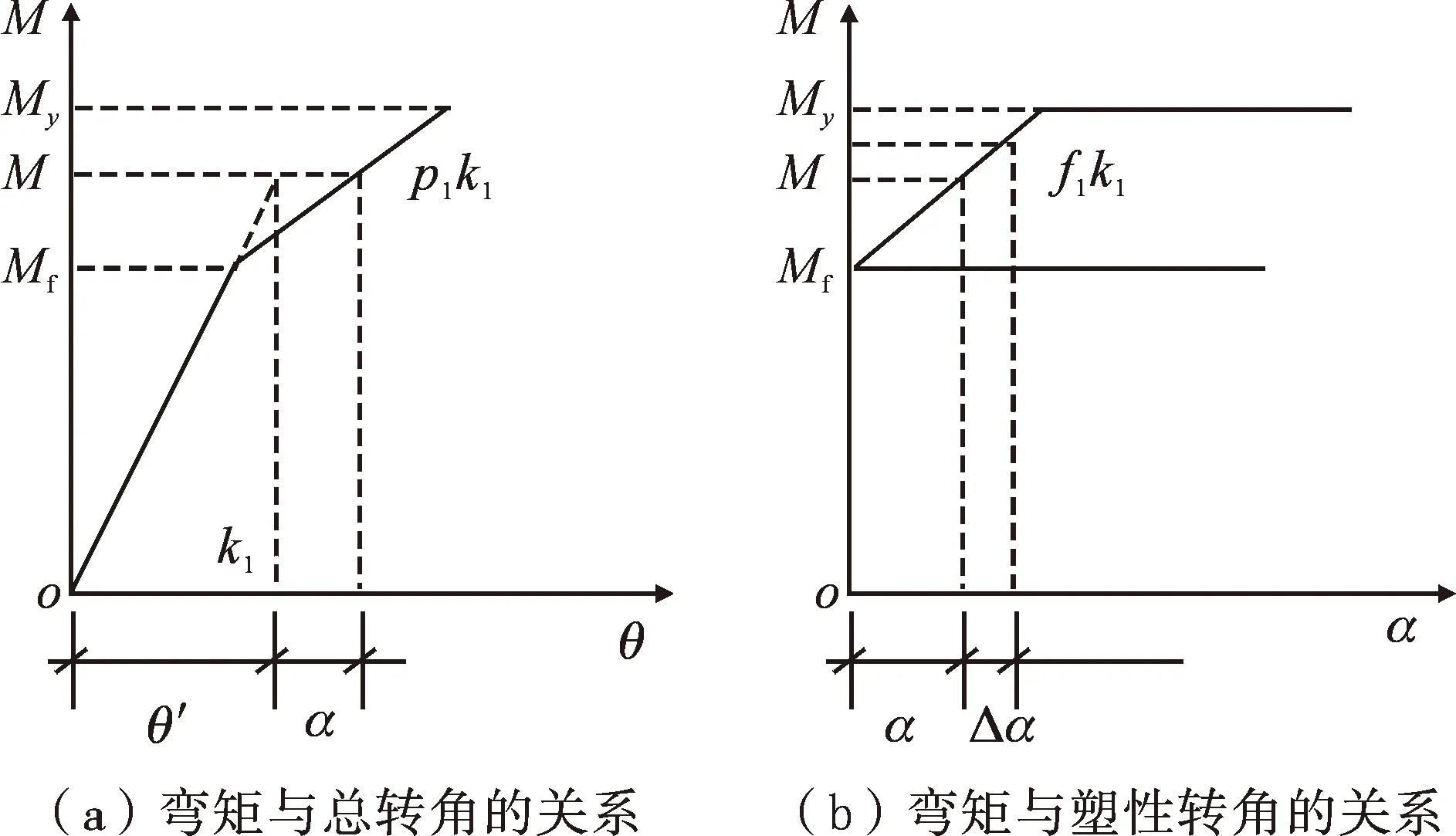
图2 弯矩与转角关系Fig.2 The relation between bending moment and corner
根据式(1),从图2(a)中可以得到
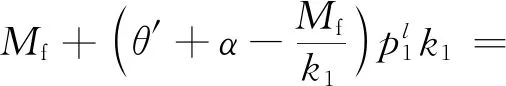
(2)
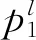
从图2(b)中可以得到
(3)
且k1=2EI/Rβ

令式(2)和式(3)相等,得到
(4)

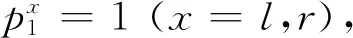
将式(4)写成矩阵形式,则
Sr=D1Sl
(5)
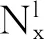
(6)
式中:p1z为扭矩与扭转角的关系中超过弹性阶段刚度的比例系数的z向分量;p1y为扭矩与扭转角的关系中超过弹性阶段刚度的比例系数的y向分量;Iy为截面惯性矩的y向分量;Iz为截面惯性矩的z向分量;f1y为扭矩与塑性扭转角的关系中超过弹性阶段刚度的比例系数的y向分量;f1z为扭矩与塑性扭转角的关系中超过弹性阶段刚度的比例系数的z向分量;E6为6阶单位矩阵。
2.2 塑性铰剪切模型
当结构的主要破坏形式为剪切破坏时,就需要用剪力V与位移v的关系的塑性铰模型来表达结构的受力特性。
v=v′+v″
(7)
式中:v为剪力位移;v′为弹性位移;v″为塑性位移。当v″为0时,杆件处于弹性变形状态。
文中表示结构的塑性变形采用剪力V与位移v的恢复力模型。图3(a)为剪力和位移的关系,图3(b)为剪力与塑性位移的关系[10]。Vf为剪力的弹性极限值;Vy为剪力的极限值;k2为弹性阶段的刚度;p2为剪力与位移v的关系中超过弹性阶段刚度的比例系数;f2为剪力与塑性位移关系中超过弹性阶段刚度的比例系数;Δv″为塑性位移增量。

图3 剪力与位移关系Fig.3 The relation between shear and displacement
根据弯曲塑性铰求解法,剪切塑性铰的点阵为
Sr=D2Sl
(8)

(9)
式中:μ为泊松比;G为剪切弹性模量;D2为剪切塑性铰的点阵;A为截面积;p2y为剪力与位移v的关系中超过弹性阶段刚度的比例系数的y向分量;p2z为剪力与位移v的关系中超过弹性阶段刚度的比例系数的z向分量。
2.3 塑性铰扭转模型
当结构的主要破坏形式为扭转破坏时,就需要用扭矩T与扭转角φ的关系的塑性铰模型来表达结构的受力特性。即
φ=φ′+φ″
(10)
式中:φ为扭转角;φ′为弹性扭转角;φ″为塑性扭转角。当φ″为0时,杆件处于弹性变形的状态。
文中表示结构的塑性变形采用扭矩T和扭转角φ的恢复力模型。图4(a)为扭矩和扭转角的关系,图4(b)为扭矩与塑性扭转角的关系[10]。Tf为扭矩的弹性极限值;Ty为扭矩的极限值;k3为弹性阶段的刚度;p3为扭矩与扭转角φ的关系中超过弹性阶段刚度的比例系数;f3为扭矩与塑性扭转角φ″的关系中超过弹性阶段刚度的比例系数;Δφ″为塑性扭转角增量。
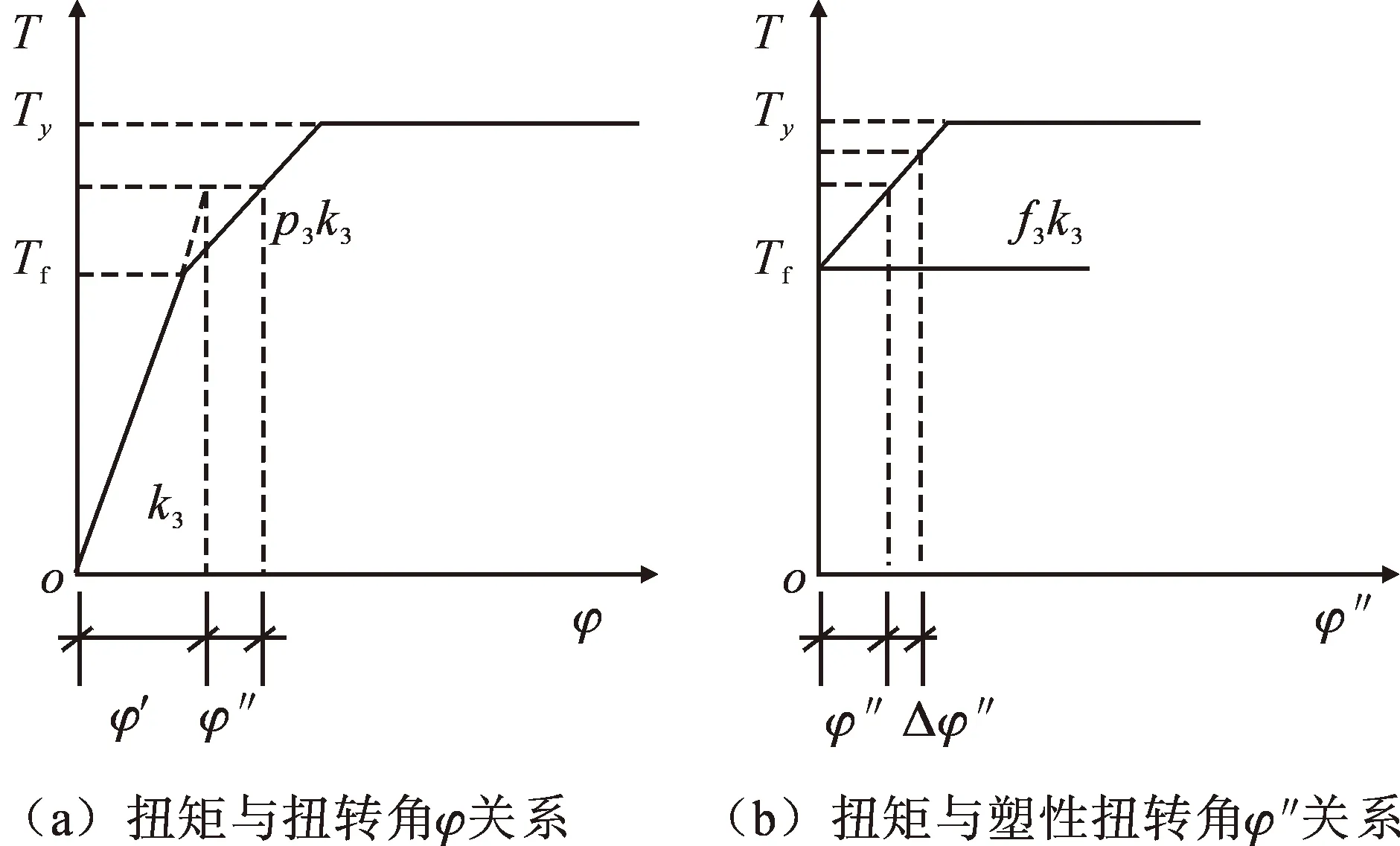
图4 扭矩与扭转角的关系Fig.4 The relation between torque and torsion angle
根据弯曲塑性铰求解法,扭转塑性铰的点阵为
Sr=D3Sl
(11)
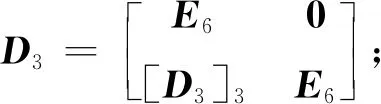
(12)
式中:It为抗扭惯性矩;D3为扭转塑性铰的点阵。
2.4 塑性铰拉压模型
当结构的主要破坏形式为拉压破坏时,就需要用轴力N与位移u的关系的塑性铰模型来表达结构的受力特性。即
u=u′+u″
(13)
式中:u为轴向位移;u′为轴向弹性位移;u″为轴向塑性位移。当u″为0时,杆件处于弹性变形状态。
文中表示结构的塑性变形采用轴向力N和轴向位移u的恢复力模型。轴力和轴向位移的关系如图5(a)所示,轴力与轴向塑性位移的关系如图5(b)所示[10]。Nf为轴力的弹性极限值;Ny为轴力的极限值;k4为弹性阶段的刚度;p4为轴力N与位移u的关系中超过弹性阶段刚度的比例系数;f4为轴力N与塑性位移u″的关系中超过弹性阶段刚度的比例系数;Δu″为轴向塑性位移增量。
根据弯曲塑性铰求解法,拉压塑性铰的点阵为
Sr=D4Sl
(14)
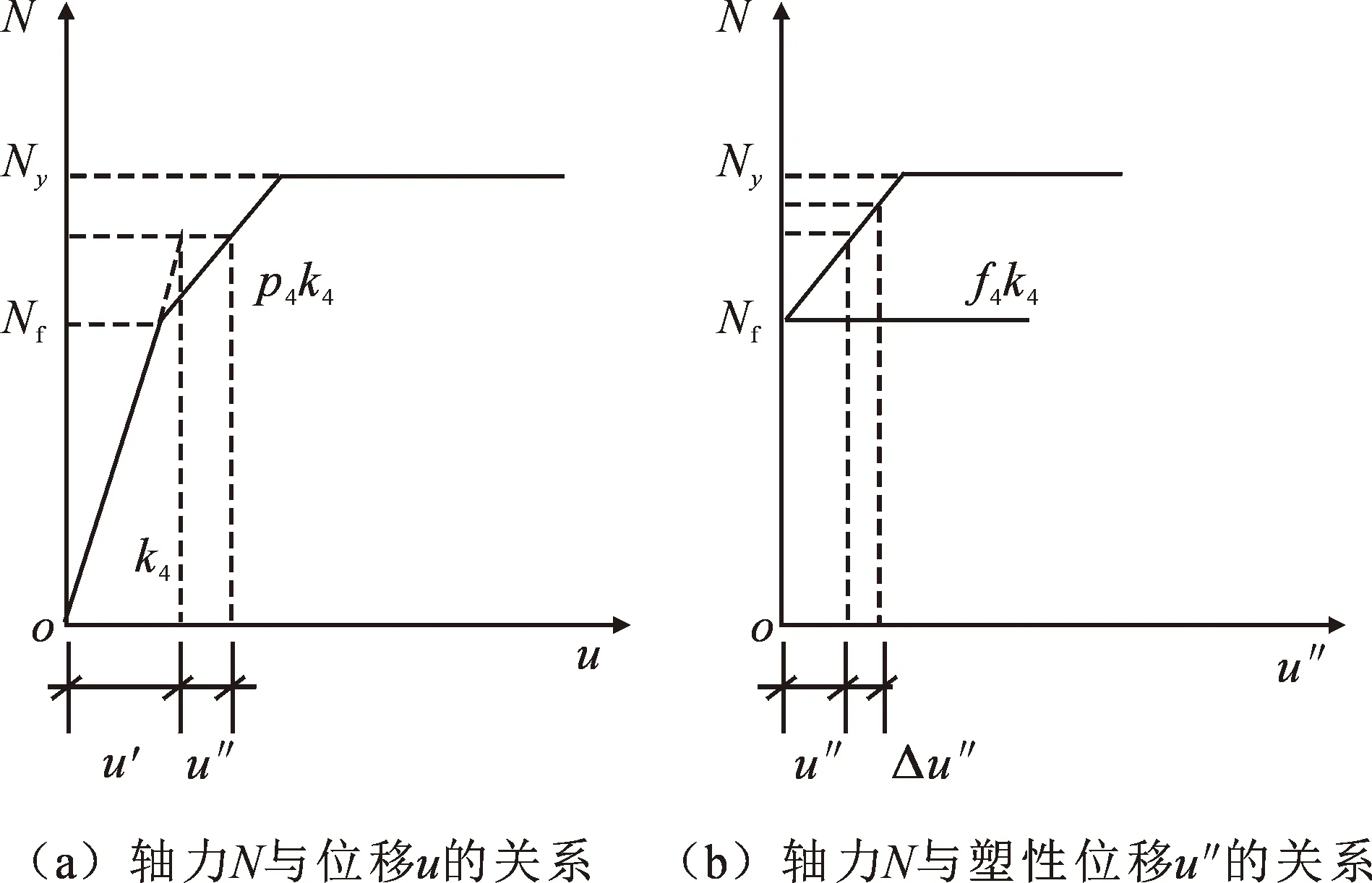
图5 轴力与位移关系Fig.5 The relation between axial force and displacement
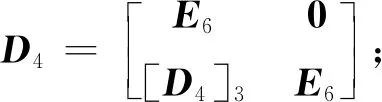
(15)
其中D4为拉压塑性铰的点阵。
曲线梁的内力和变形计算都较为复杂,存在“弯-扭”耦合效应,可以将多种塑性铰模型合并应用。此时塑性铰的点阵为
[D]3=
(16)
3 实例计算
桥梁结构在地震作用下会发生不同程度的损伤破坏,结构进入弹塑性变形阶段和混凝土碎裂破坏阶段的时候,假定混凝土的压碎失效和钢筋的屈服失效同时发生,取混凝土进入破坏失效阶段的许用应力[σ]=35 N·mm-2,进入弹塑性阶段的许用应力为0.4[σ][12]。
某5跨钢筋混凝土曲线连续箱梁桥,支座弹簧的刚度为kz=7.2×103MPa·m-1,ky=3.65 MPa·m-1,kx=4.95×103kN·m-1,具体模型尺寸如图6~7所示,参数见表1。q为分布力;P为集中力;Iω为截面扇形惯性矩。
该算例将进入破坏失效阶段的许用应力值转化为许用弯矩值[M2]=43 360 kN·m,进入弹塑性阶段的许用应力值转化为许用弯矩值为[M1]=17 344 kN·m,弹性编程结果显示,最大弯矩为1.8×104kN·m,此弯矩值超过了弹性阶段的最大弯矩值,采用弹塑性塑性铰编程来计算(取p1y=p1z=0.5),结果如图8所示。
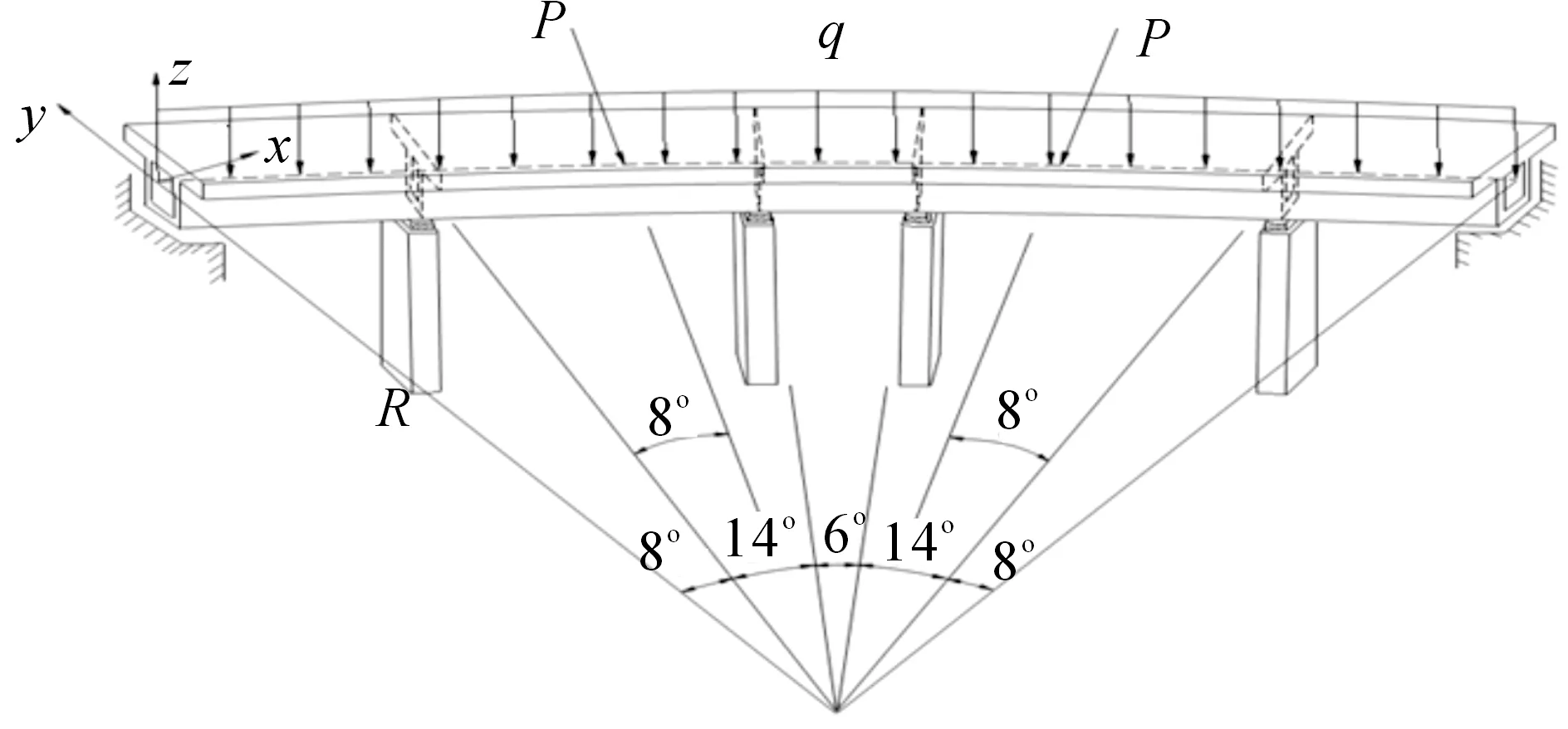
图6 计算模型Fig.6 The calculation model

图7 计算简图Fig.7 The calculation diagram
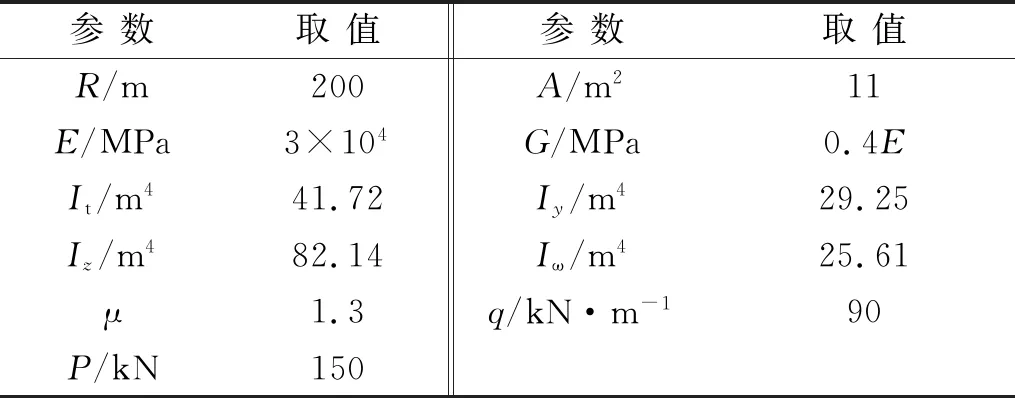
表1 曲线梁的基本参数Tab.1 The basic parameters of a curved beam
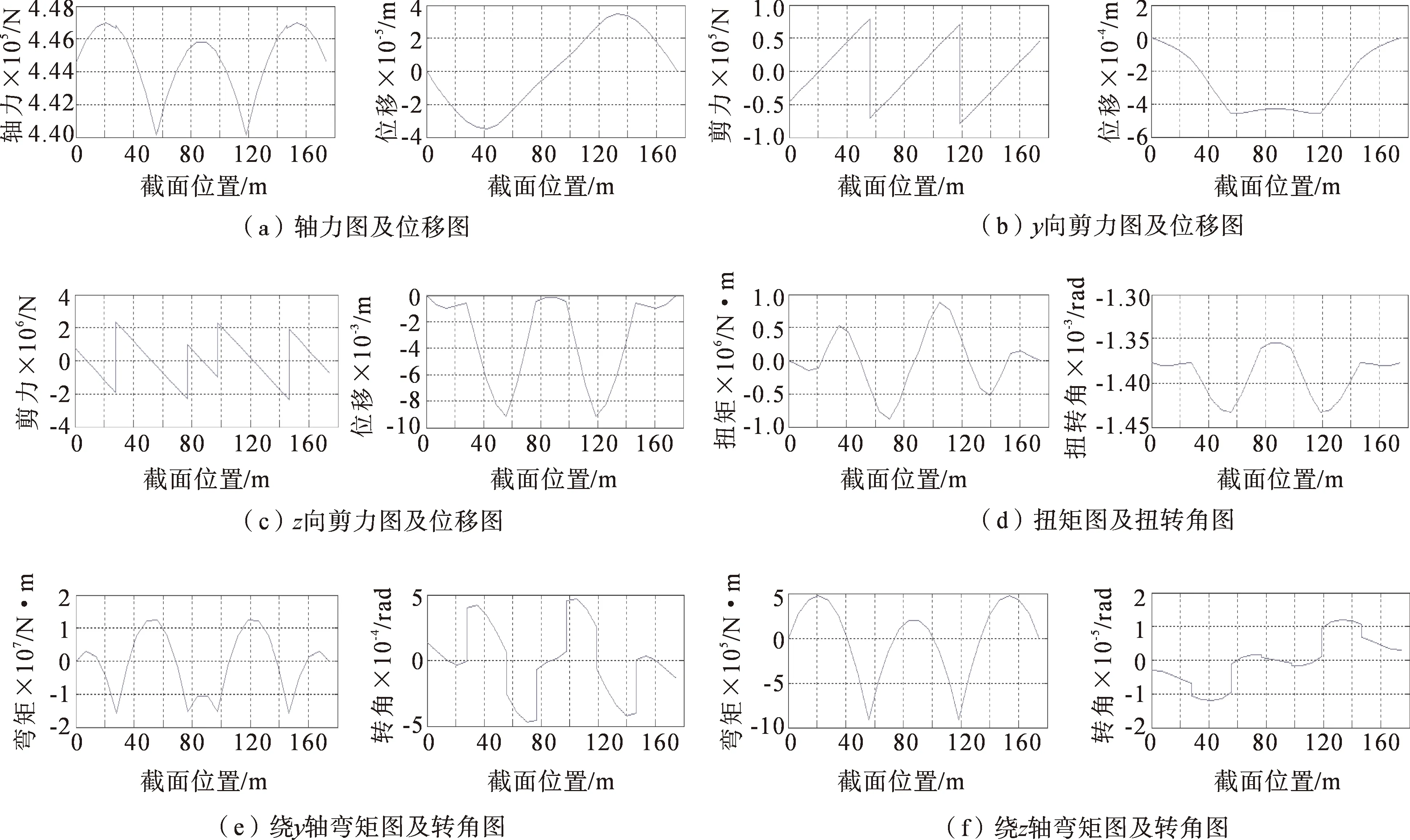
图8 曲线梁的内力及变形图Fig.8 Theinternal force and deformation of a curved beam
4 结 论
1)文中通过对曲线梁的弹塑性模型的分析,采用辅助体系法导出了曲线梁桥不同塑性铰(塑性弯曲铰模型、塑性剪切铰模型、塑性扭转铰模型以及塑性拉压铰模型)的传递矩阵。
2)通过实例计算,表明可采用辅助体系传递矩阵法对结构进行弹塑性分析,此方法相比有限元的方法更加简便实用,为空间曲梁的结构分析提供了理论和方法。

