初中数学“顺敞悟”的教学理解

江苏省苏州工业园区星洋学校 杨雪华

教学实践中，我们经常会遇到教师的讲解与学生的理解之间的“不和谐”“唤不醒”“点不燃”，有时甚至出现“讲了几遍学生还是不会”的尴尬，到底是哪个环节出了问题？是教得不清？学得不实？还是内容太难？无法理解或是无法掌握？这些现象在教师的工作中时常出现。笔者调查后发现，这些问题其实是教师的“教”与学生的“学”的脱节，数学课堂中学生“理解”“掌握”“应用”的前提首先应该是“接受”，一种自然而然的对知识的“认可”。如果学生的想法“不敞”，教师的教法“不顺”，其结果就是师生间的沟通貌似相通，实则神离，进而大大影响了教学效果。下面，笔者通过例子来谈谈这个问题。

一、“顺”模型，“敞”根源——“悟”线段最值转化

《数学课程标准》指出：数学课程内容要符合学生的认知规律，要贴近学生的实际，有利于学生体验与理解、思考与探索，教师教学应该以学生的认知发展水平和已有的经验为基础，注重启发式和因材施教。

1.原题呈现

问题：如图（1），已知A、B是两个定点，在定直线l上找一动点M，在平面内找一动点N，直线MN的方向确定（即直线MN与直线l右侧部分相交所得的锐角为α），且MN等于定长d，使AN+NM+MB最小。

图（1）

分析：要求AN+NM+MB的最小值，这是动线段的最值问题，因为MN等于定长d，所以只需求AN+MB的最小值即可。于是将三条动线段的最值问题转化为两条动线段的最值问题。

那么怎样解决呢？分析到此处，学生可能还是难以突破，教师要顺着学生的思路，提出关键一问：“线段怎么会运动的？”得出本题的实质，即为“点动线动”，转化为动点最值问题，还原出数学问题的本质。此时如果学生还有不解，我们可以顺着学生已经认可的“点动”最值，引出如下两个模型。

2.顺导敞思

联想生成1——“将军饮马”模型：如图（2），图（3），在定直线l上找一个动点P，使动点P到两个定点A与B的距离之和最小，即PA+PB最小。

图（2）

图（3）

分析：如图（2），连接AB交l于点P，即为所求的直线l上的点。如图（3），作点A关于直线l的对称点A′，连接A′B交l于点P，即为满足条件的直线l上的点。这个“两点一线”模型，学生应该没有太大问题。

联想生成2——“行船运货”模型：如图（4），已知A、B是两个定点，在定直线l上找两个动点M与N，且MN等于定长d（动点M位于动点N左侧），使AM+MN+NB最小。

如图（4），要求三条线段AM+MN+NB的最小值，而这三条线段恰好构成一条折线，学生的第一想法是运用“折线大于直线”思想，连接AB即为最小值；但画图发现AB与l只有一个交点，这个交点是M还是N呢？学生出现思维的矛盾。再进一步，直线l上需要找两个动点M与N，但这两个动点是相互牵制、彼此影响的，不过保持MN等于定长d（且动点M位于动点N左侧），也就是当动点M确定下来，动点N也会随之向右平移d个单位确定下来。“顺藤摸瓜”，教师将学生的思路很自然地引导到了“平移”。学生认可“平移”后，思维基本敞开，原问题便可转化为线段AM+NB的最小值。如图（5），将定点A沿着定直线l的方向向右平移d得到点C，构造出平行四边形ACNM，就有AM+NB=CN+NB，于是要求AM+NB最小，只需求CN+NB最小。连接CB，与定直线l的交点N即为所要寻找的点N，而点M只需将点N向左平移d个单位即可找到，此时AM+MN+NB的最小值问题便迎刃而解了。

图（4）

图（5）

3.感悟深究

如图（6），已知A、B是两个定点，在定直线l上找两个动点M与N，且MN等于定长d（动点M位于动点N左侧），使AM+MN+NB最小。用类比的思想，让学生自行解决。

图（6）

图（7）

4.问题反刍，领悟生成

现在我们重新回到本文开始的问题探究。如图（1），点A、B是定点，在定直线l上找一动点M，在平面内找一动点N，直线MN的方向确定（即直线MN与直线l右侧部分相交所得锐角为α），且MN等于定长d，使AN+NM+MB最小。

学生有了前面的铺垫和积累，分析解决就会游刃有余了。如图（7），将定点A沿着NM的方向，向左下方平移d个距离得到点C，构造出平行四边形ACMN，就有AN+MB=CM+MB，要求AN+MB的最小值，只需求CM+MB的最小值，顺利将本问题转化为了如图（2）的问题。连接CB，与定直线l的交点M即为所要寻找的点M，再将点M作相应平移即可找到点N，此时AN+NM+MB最小，且等于d+CB。

二、“顺”学识，“敞”心智——“悟”教学真与实

1.原题呈现

问题：已知点P是抛物线y=ax2+c上一个动点，且点P到直线y=－2的距离始终等于PO（O为坐标原点），则该抛物线的解析式为__________ 。

2.顺导敞思，真实面对

教学实践发现，学生读题后对抛物线解析式y=ax2+c感到困惑，参数a、c不确定导致无从下手。教师读题顺势而为，“既然a、c不确定，那该怎样处理呢？”顺引出“分类讨论”，画出可能情形。

举例如下：如图（8），当点P运动到抛物线的顶点时，点P到原点O的距离与点P到直线y=-2的距离一定不相等。此种情况可排除。

如图（9），教学时引导学生找出反例。当点P运动到抛物线与直线y=-2的两个交点时，此时点P到原点O的距离与点P到直线y=-2的距离一定不相等。此种情况也可排除。

图（8）

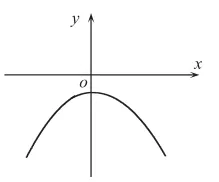
图（9）

图（10）

综合考虑后，得出只有图（10）符合题意。

解析：设点P坐标为(x，y)，则PO2=x2+y2。可得点P(x，y)到直线y=-2的距离d=|y+2|，由题意得d2=PO2，即：x2+y2=|y+2|2，即x²+y²=y²+4y+4，得所以该抛物线解析式为

笔者倡导的数学课堂教学的“顺敞悟”的实质是顺学情、顺学力、顺学生的心智，敞基础、敞思维、敞学生已有的认知和经验，探索一种纯自然的、质朴的教学体验，接受、认可、理解、内化、铭刻乃至以不变应万变的运用。师生双方的教学活动犹如“心有灵犀一点通”。这一“点”正是四两拨千斤，使学生能走出疑惑、跳出迷局、学的轻松、学出成效。笔者愿和各位读者共同探索，努力实现“内容清楚、过程简单、思维顺敞、感悟真切、效果显著”的初中数学高效课堂。