几类有限交换群的整群环的K1群*

王祚恩，唐国平

(中国科学院大学数学科学学院， 北京 100049)

本文报道我们在利用核群D(ZG)研究K1(ZG)时得到的一些结果。

1 预备知识

定义1.1设R是一个有单位元 1 的环，有限生成投射R-模M的同构类记为[M]，则在集合Proj(R)={[M]|M是有限生成投射R-模}上定义加法运算[M]+[N]=[M⊕N]，使得Proj(R)成为一个有零元0的交换半群，K0(R)定义为Proj(R)的群完备化。

设f:R→S是一个环同态，则S可以看成S-R双模，故对左R-模M，有S⊗RM是左S-模，当M是有限生成投射R-模时，S⊗RM是有限生成投射S-模。

由此可建立群同态K0(f):K0(R)→K0(S), [M]→[S⊗RM]。

定义1.2设R是一个诺特整环，商域为K，A是一个有限维K-代数。A的一个R-序(R-order)Λ是A的一个子环，同时是A的有限生成R-子模，并满足K·Λ={∑αimi:αi∈K,mi∈Λ,其中∑表示有限和}=A。

设G为有限群，易见ZG为QG中的一个Z-序(Z-order)。

现考虑QG中的任意一个Z-序Λ，设p为任意的素数，则整数环Z有素理想(p)，令Λ(p)表示Λ在素理想(p)处的局部化，则有：K0(Λ)→K0(Λ(p)),[M]→[Λ(p)⊗ΛM]。

定义1.3设Λ是半单代数QG的一个Z-序，Γ是QG中包含Λ的一个极大Z-序，则有同态η：CL(Λ)→CL(Γ)，将[M]映射为[Γ⊗ΛM]，其中M是一个有限生成投射Λ-模，核群D(Λ)定义为映射η的核。

注：QG中包含Λ的极大Z-序一般不唯一，但核群D(Λ)与极大Z-序Γ的选取无关(见文献[1])。

由Whitehead引理可知，E(R)=[GL(R),GL(R)]=[E(R),E(R)]，因此E(R)◁GL(R)且E(R)为完全群。记K1(R)=GL(R)/E(R)，称交换群K1(R)为环R的K1群。

对于任意群G,{±g:g∈G}⊆(ZG)×⊆GL(ZG),将{±g:g∈G}对应于K1(ZG)的元素生成的子群记为±G,则称Wh(G)=K1(ZG)/±G为G的Whitehead群。关于Whitehead群的更多信息见文献[2]。

设R是一个有单位元1的交换环,用R×表示环R的单位群,则行列式映射诱导出K1(R)到R×的满同态,并且有分裂同态R×→K1(R),因此有K1(R)=R×⊕SK1(R)。其中SK1(R)=SL(R)/E(R),SL(R)是GL(R)中行列式为1的矩阵构成的群。

注1：若F是代数数域，R是F的代数整数环，则由文献[3]可知SK1(R)=0。

注2：对于整群环ZG，文献[2]给出了SK1(ZG)=0的充分必要条件。

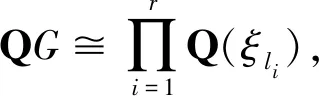
证明见文献[4]。

引理1.2在引理1.1的假设下,(ZG)×的挠部分即为{±g∶g∈G},且(ZG)×自由部分的秩等于Γ×自由部分的秩。特别地,[Γ×∶(ZG)×]<+∞。

证明见文献[5]。

定义1.5在引理1.1的假设下，令ZGp=ZG⊗ZZp，Γp=Γ⊗ZZp，其中Zp为p-adic整数环。Z中的素理想(p)称为ZG-奇异，如果Γp≠ZGp。 记S(ZG)为ZG-奇异素理想的集合。

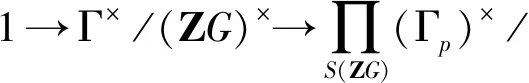
且有：

(ii)[(Γp)×∶(ZGp)×]=lpmp,

其中Jp为Γp的Jacobson根。

证明见文献[6]。

证明见文献[4]。

由文献[2]可知,对于一些有限交换群G,SK1(ZG)=0,此时K1(ZG)=(ZG)×。又由引理1.2,此时G的Whitehead群Wh(G)即为有限生成交换群K1(ZG)的自由部分,且其秩与有限生成交换群K1(Γ)=Γ×自由部分的秩相等。由于此时K1(Γ)与K1(ZG)的挠部分均显然,根据有限生成交换群的结构定理，计算出[K1(Γ)∶K1(ZG)]就可以估计K1(Γ)自由部分的生成元与K1(ZG)自由部分的生成元之间的倍数关系,本文的第2节和第3节主要对此进行计算。

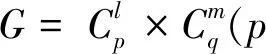
lp=(p-1)pl-1+pl-2+…+p+1×

(pf-1)g(pl-1+pl-2+…+p+1)(qm-1+qm-2+…+q+1),

lq=(q-1)qm-1+qm-2+…+q+1×

(qf ′-1)g′(pl-1+pl-2+…+p+1)(qm-1+qm-2+…+q+1),

证明

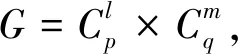
归纳可得

QG=Q×Q(ω)pl-1+pl-2+…+p+1×

Q(η)qm-1+qm-2+…+q+1×

Q(λ)(pl-1+pl-2+…+p+1)(qm-1+qm-2+…+q+1).

2)由引理1.1，

Γ=Z×Z[ω]pl-1+pl-2+…+p+1×

Z[η]qm-1+qm-2+…+q+1×

Z[λ](pl-1+pl-2+…+p+1)(qm-1+qm-2+…+q+1).

由pZ[ω]=(1-ω)p-1，N(1-ω)=p。

可得Q(ω)⊗QQp=Q(ω)(1-ω)，即Q(ω)对Z[ω]中素理想(1-ω)的局部域。

记O(1-ω)为其赋值环，M(1-ω)为O(1-ω)唯一的极大理想。易见O(1-ω)为Zp在Q(ω)(1-ω)中的整闭包。

再记O′为Q(ω)的赋值环，M′为O′唯一的极大理想。

由局部域的性质可得O(1-ω)/M(1-ω)=O′/M′=Z[ω]/(1-ω)=Fp，即p阶有限域。

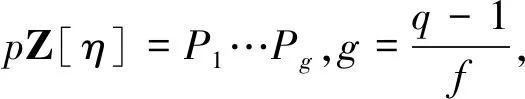
可得Q(η)⊗QQp=Q(η)P1×…×Q(η)Pg，记号同上，有OPj/MPj=Z[η]/Pj=Fpf。

因此QG⊗QQp=Qp×(Q(ω)(1-ω))pl-1+…+p+1×(Q(η)P1×…×Q(η)Pg)qm-1+qm-2+…+q+1×(Q(λ)P′1×…×Q(λ)P′g)(pl-1+…+p+1)(qm-1+…+q+1)。

由引理1.4可知，Γp/Jp=Fp×

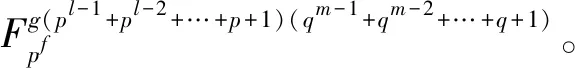
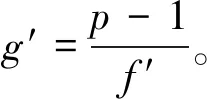
3)ZGp/Jp∩ZGp=Fp[Cq×…×Cq]=Fp[Cq]⊗Fp…⊗FpFp[Cq]。

由于有限域的有限扩张为Galois扩张，设Fpf=Fp(θ)，φ为θ在Fp上的极小多项式，则φ在Fpf上分裂。

所以Fpf⊗FpFpf=Fpf[x]/(φ)=Ffpf。

4)记d(Γ)为Γ的判别式，因此d(Γ)=p(p-2)(pl-1+pl-2+…+p+1)·q(q-2)(qm-1+qm-2+…+q+1)·(p(p-2)(q-1)·q(q-2)(p-1))(pl-1+…+p+1)(qm-1+…+q+1)=pqm(pl-1-pl-1-pl-2-…-p-1)·qpl(qm-1-qm-1-qm-2-…-q-1)，记d(ZG)为ZG的判别式，d(ZG)=(plqm)plqm。

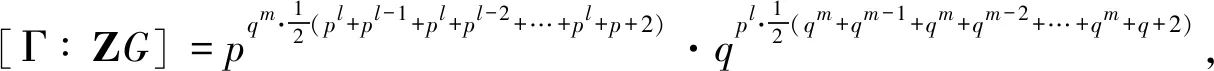
5)由引理1.3，

lp=(p-1)pl-1+pl-2+…+p+1×

(pf-1)g(pl-1+pl-2+…+p+1)(qm-1+qm-2+…+q+1),

lq=(q-1)qm-1+qm-2+…+q+1×

(qf′-1)g′(pl-1+pl-2+…+p+1)(qm-1+qm-2+…+q+1),

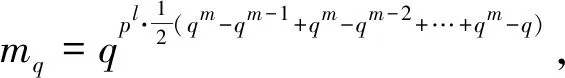
定理2.2

(i)当G=Cp时,[K1(Γ)∶K1(ZG)]=p-1.

证明由定理2.1可得

|D(ZG)|·[Γ×∶(ZG)×]=p-1.

又|D(ZG)|=1(见文献[8]),

因此[Γ×∶(ZG)×]=p-1。

由文献[2]可知此时SK1(ZG)=0,所以[Γ×∶K1(ZG)]=p-1。

又Γ为有限个代数整数环的乘积,K1与取单位群均与有限乘积交换,由文献[3]可知K1(Γ)=Γ×。

因此得到[K1(Γ)∶K1(ZG)]=p-1。

(ii)当G=C2×Cp时,其中p为奇素数。

则有(p-1)2|[K1(Γ)∶K1(ZG)],[K1(Γ)∶K1(ZG)]|(2f ″-1)g ″·(p-1)2/N(2,p),

特别地

当G=C2×C5时,[K1(Γ)∶K1(ZG)]=240。

当G=C2×C7时,[K1(Γ)∶K1(ZG)]=1 764。

证明由定理2.1可得

|D(ZG)|·[Γ×∶(ZG)×]=(2f ″-1)g ″·(p-1)2.

由文献[9]可知D(ZG)为(Z[ω]/2Z[ω])×的商群,Z[ω]/2Z[ω]=F2f ″×…×F2f ″,因此|D(ZG)||(2f ″-1)g ″,可得 (p-1)2|[Γ×∶(ZG)×],类似于(i), 此即(p-1)2|[K1(Γ)∶K1(ZG)]。

又由文献[10]可知N(2,p)||D(ZG)|, 因此[K1(Γ)∶K1(ZG)]|(2f ″-1)g ″·(p-1)2/N(2,p)。

特别地,当G=C2×C5时, 由文献[11]可知|D(ZG)|=1,所以[K1(Γ)∶K1(ZG)]=16×15=240。

当G=C2×C7时，同样有|D(ZG)|=1,所以[K1(Γ)∶K1(ZG)]=36×49=1 764。

(iii)当G=Cp×Cq时,其中p与q为不同的奇素数。

则有

[K1(Γ)∶K1(ZG)]|

其中f,g,f′,g′的定义与定理2.1一致,

N(q,p)的定义类似。

证明由定理2.1可得|D(ZG)|·[Γ×∶(ZG)×]=(p-1)·(pf-1)g·(q-1)·(qf ′-1)g ′。

由文献[10]可知N(p,q)·N(q,p)|4·|D(ZG)|。

类似于(i),[Γ×∶(ZG)×]即[K1(Γ)∶K1(ZG)]。所以有[K1(Γ)∶K1(ZG)]|

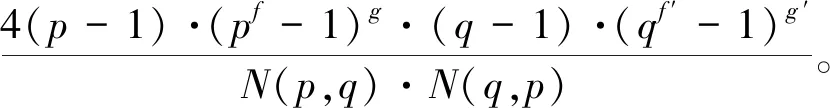
3 G=Cpn+1时的情形

定理3.1G=Cpn+1(n≥0，p为正则奇素数,Cpn+1表示pn+1阶循环群)时,[K1(Γ)∶K1(ZG)]=(p-1)n+1·p1+p+p2+…+pn-(n+1)-h,

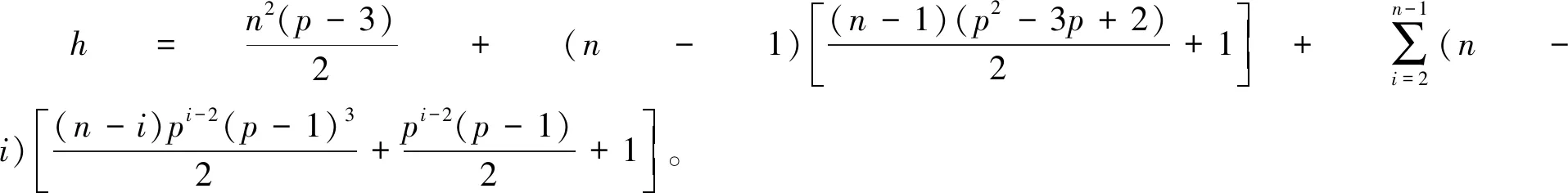
可得Γ=Z×Z[ω1]×Z[ω2]×…×Z[ωn+1]。

类似定理2.1,QG⊗QQp=Qp×Q(ω1)(1-ω1)×…×Q(ωn+1)(1-ωn+1),

类似定理2.1,lp=(p-1)n+1,mp=p1+p+…+pn-(n+1),|D(ZG)|·[Γ×∶(ZG)×]=|D(ZG)|·[K1(Γ)∶K1(ZG)]=(p-1)n+1·p1+p+p2+…+pn-(n+1)。又由文献[12]可知

因此|D(ZG)|=ph,

所以[K1(Γ):K1(ZG)]=(p-1)n+1·p1+p+p2+…+pn-(n+1)-h。