Effect of broad bounce on primordial gravitational waves*

ZHAO Jinyun, PIAO Yunsong

(School of Physics Sciences, University of Chinese Academy of Sciences, Beijing 101408, China)

Abstract The bounce inflation is successful in solving the initial singularity problem of inflation and is also competitive in explaining the power deficit in CMB at large scale. Generally, the duration that the bounce lasts is short (the so-called narrow bounce). However, the case of broad bounce is not ruled out. In this study, we focus on the tensor perturbation during the inflation with a broad bounce. We find that the power spectrum may be very different from that in narrow bounce model.

Keywords bounce inflation; gravitational waves; power spectrum

Inflation[1-3], as the paradigm of the early universe, is a fundamental model of the cosmology. It has not only solved the problems of the big bang theory but also provided the primordial scalar and tensor perturbations that generate the large-scale structure[4]. However, because of the so-called “singularity problem”, inflation theory needs to be improved. An acceptable way to solve the problem is considering the so-called bounce inflation scenario[5-7](see also Refs.[8-17]). In bounce inflation, there is a contracting phase after a bounce phase the inflation starts. Recently, the development of effective field theory of nonsingular cosmologies[18-20]has made us construct full stable bounce models.

The evidence, that is, the power deficit of the CMB TT-mode spectrum at large scale observed by the Plank collaboration makes physicists to consider the physics before inflation[21]. The bounce model is accepted by many workers in order to solve the problem above, which has been reviewed in Refs.[22-23].

Primordial gravitational waves (GWs) open an important window for exploring the early universe. Recently, a large number of experiments aiming at observing GWs have been implemented or will be implemented[24]. Thus understanding about the early universe and inflation scenario will be deeper and deeper. Since the primordial GWs are independent of the dynamics of the scalar field, it can be used to identify the physics of the pre-inflation background. In a previous work[25], GWs of bounce model has been studied, in which the duration that the bounce lasts is short (the so-called narrow bounce). However, the case of broad bounce is not ruled out. In this study, we focus on the GWs from the bounce inflation with a broad bounce.

1 Tensor perturbation in bounce inflation scenario

In bounce inflation scenario, the universe experiences a phase, showed in Fig.1, before inflation, in whichavarying withηis the scale factor of the universe,ηB-is the beginning time of bounce phase,ηBis the so-called bounce point at which Hubble ConstantH=0, andηB+is the ending time of bounce phase. By contrast to the previous work, contracting phase does not keep symmetric to inflation, which also means HB-≠-HB+.

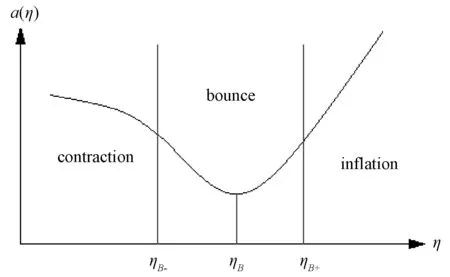
ηB is the so-called bounce point.Fig.1 The bounce phase occurring between ηB- and ηB+

We start with the second order perturbation action in which tensor perturbationγijpresents the physical message in this time,

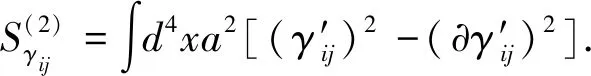
(1)

The equation of motion turns as

(2)

In contracting phase, the scale factor can be parameterized as

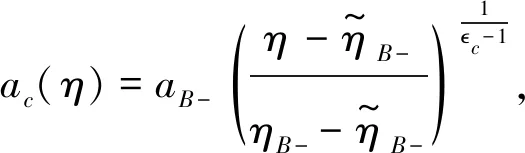
(3)

(4)

for the initial state. The solution of equation is

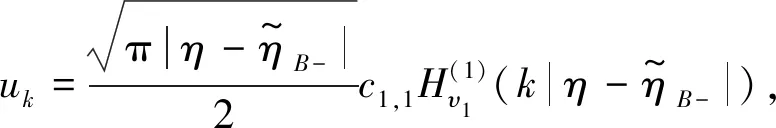
(5)

In bounce phase, the scale factor can be parameterized as

(6)

Then the equation of motion, to the first order ofη, is

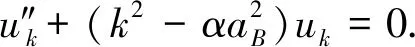
(7)

The corresponding solution is

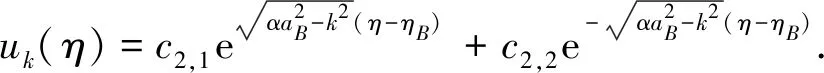
(8)

However, for the broad bounce, where the bounce time Δη～1/aB, the second order ofηshould be considered, and the equation of motion is

(9)

The corresponding solution is

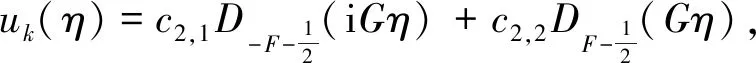
(10)

In inflationary phase, the scale factor is

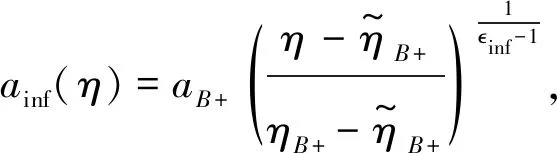
(11)

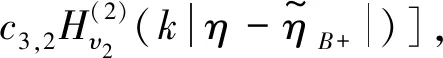
(12)

1.1 Narrow bounce

We first consider the narrow bounce (8). Using the continuous condition that the solution and its derivative of different phases should be continuous atηB-point andηB+point, one can get the transport matric

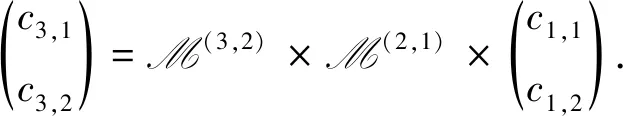
(13)

The matric elements of M(2,1)are

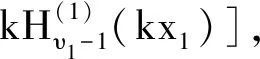
(14)

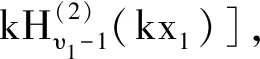
(15)

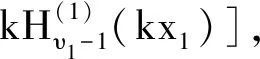
(16)

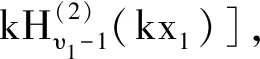
(17)

and the matric elements of M(3,2)are

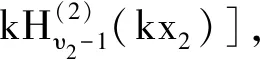
(18)

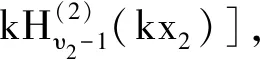
(19)

(20)

(21)

For largekand smallk-mode approximations, we have

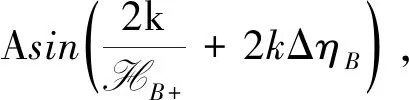
(22)

(23)

for smallk, where

1.2 Broad bounce

Now we consider the broad bounce (10). Because of the complex mathematical expression, we only give some conclusions. For example, the first matric element of M(2,1)is

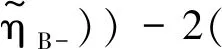
aB(1-c)(ηB--

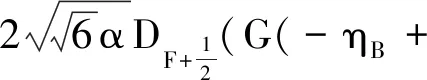
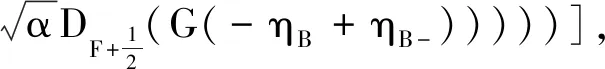
(24)

and the first matric element of M(3,2)is

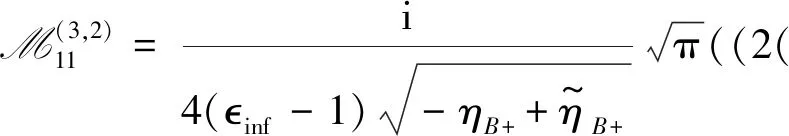
ηB+)))).

(25)

The other matric elements are omitted here.

2 The figures of power spectrum

Using the technology and above conclusion to get |c3,1-c3,2|2, namelyPT, we get the power spectrum of tensor perturbation in bounce inflation.

Figure 2 shows the spectra with different bounce durations. Considering that the bounce no longer contains symmetry in broad bounce, we plot Fig.3, in which the first wave crest of spectrum is depressed with the increasing of asymmetry of bounce shape at a determined bounce duration, and this feature turns more obvious in broad bounce.

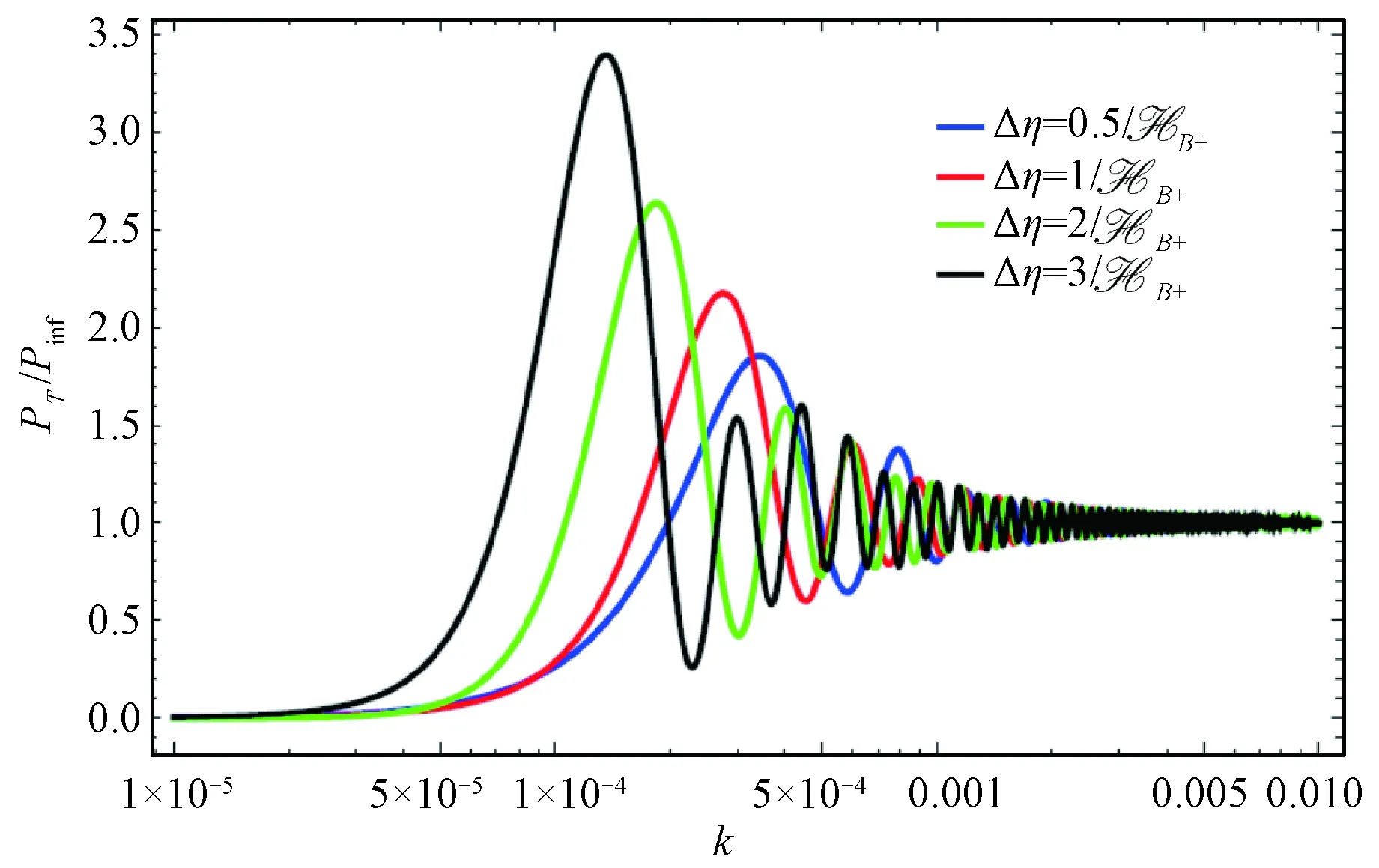
Fig.2 HB-=-HB+

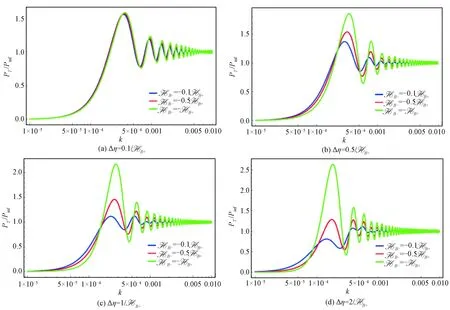
Fig.3 Power spectra with different bounce times

Figures 4(a), 4(b), and 4(c) show the differences between the narrow and broad bounces. The curve of the second order turns to be abnormal when bounce turns to be broad. Though the bounce inflation has not been verified by experiment, some fitting studies have been carried out, such as Ref.[25]. If we detect the power spectrum in such a shape in future, we can accurately check the theory and distinguish between the broad bounce and the narrow bounce.

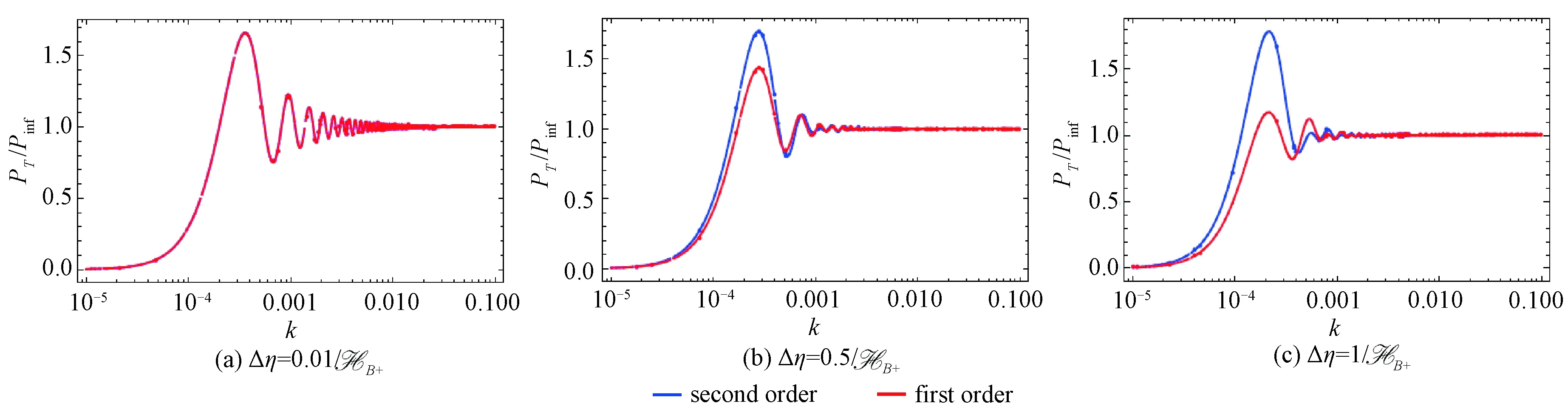
The first order for narrow bounce, and the second order for broad bounce.Fig.4 Contrast between narrow bounce and broad bounce

3 Discussion

The bounce inflation is successful in solving the initial singularity problem of inflation and is also competitive in explaining the power deficit in CMB at large scale. This might provide a chance to comprehend the origin of inflation thoroughly. Theoretically, previous work successfully deals with the case with the narrow bounce. It is not only for a much extensive prediction, but also for the completion of the theory. We naturally generalize the narrow bounce to the broad bounce. In this study, we calculate the tensor perturbation in the bounce inflation scenario with the broad bounce. We get the result in a more precise approximation, and compare our result with that in narrow bounce model.