钢弹簧浮置板轨道对箱梁振动声辐射的影响研究
李小珍, 聂 骏, 郭 镇, 王党雄, 朱 艳
(西南交通大学 桥梁工程系,成都 610031)
列车激励引起高架桥振动并产生低频噪声,这一问题正逐渐引起人们的重视。针对高架桥结构进行声学优化设计可改变梁体的声辐射特性,控制桥梁下部结构辐射的噪声[1-2];针对轨道结构采取减振措施能够从源头上控制噪声,其中,浮置板轨道因具有优秀的减振降噪性能,在目前已建成的城市轨道交通线中得到了广泛应用。
国内外研究者对浮置板的减振性能进行了大量的研究。在理论分析方面,文献[3-5]分别建立了浮置板轨道结构的解析模型,研究了浮置板轨道结构的隔振性能,分析了相对位移激励下轮轨间动载荷和传递给基础的力;文献[6]建立了能反映浮置板轨道动态特性的力学模型,探讨了浮置板轨道减振特性的影响因素;文献[7]以单位简谐力作为激励,不考虑车辆-轨道耦合作用,分别建立了短、中、长三种浮置板轨道模型,对其减振性能进行了研究;文献[8]采用模态分析方法,通过正交试验探讨了钢弹簧浮置板参数变化对其动力特性的影响;文献[9]建立了钢弹簧浮置板轨道动力分析有限元模型,研究了不同参数下浮置板轨道的隔振效率,指出隔振弹簧的刚度和阻尼是首要影响因素;在试验研究方面,文献[10-11]通过对浮置板轨道的减振效果进行了现场测试;文献[12]通过1∶1模型试验对钢弹簧浮置板轨道和普通轨道的低频减振效果进行了比较,发现相对于普通轨道,钢弹簧浮置板轨道的最大减振量达25 dB。
近年来,研究人员开始关注浮置板轨道对轨下桥梁结构的振动影响。例如,文献[13]分别采用有限元和现场试验方法,在时域、频域内对高架钢弹簧浮置板轨道结构的减振特性进行了分析;文献[14]采用动柔度法,建立了3层Euler梁模型,对比了桥上CRTS-I型板式无砟轨道和浮置板轨道在各种参数下的振动特性;文献[15]采用数值方法就浮置板轨道对箱梁中高频振动的影响规律及原因进行了研究。不难发现,上述研究仍未涉及浮置板轨道对箱梁声辐射的影响。
本文首先采用动柔度法建立频域内列车-轨道耦合振动的解析模型,并采用有限元模型求解箱梁振动响应,然后在频域内采用边界元法计算箱梁结构噪声,最后采用现场试验结果验证理论模型。在此基础上,采用数值方法对比普通板式轨道和钢弹簧浮置板对箱梁声辐射的影响,并选取扣件刚度、钢弹簧刚度、浮置板长度和浮置板厚度等参数进行参数分析。本文的研究成果可为箱梁上浮置板轨道结构的选型和设计提供理论依据。
1 仿真分析模型
本文在频域内进行箱梁振动声辐射分析。具体思路如下:首先,建立列车-轨道耦合振动模型,通过解析方法得到传递至箱梁的激励力;然后,采用板单元建立箱梁有限元模型,以前述激励力进行谐响应分析,获得箱梁振动响应;最后,将箱梁有限元网格转换为边界元网格,以箱梁振动响应为声学边界,利用声学边界元法分析箱梁声辐射。
1.1 列车-轨道耦合振动模型
相关研究表明[16]:混凝土箱梁的声辐射频率主要集中在20~200 Hz以内,其来源于箱梁局部振动响应。在该频率范围内,桥梁对轨道系统的支承刚度远大于轨道系统自身的刚度,故可将轨道系统的支承刚度视为无穷大。
本文重点对钢弹簧浮置板轨道的减振降噪行为进行分析,并与普通板式轨道进行对比。两种轨道结构的示意图,如图1所示。

(a) 钢弹簧浮置板

(b) 普通板式轨道
本文建立的列车-轨道耦合振动模型如图2所示。从图2可知,L1表示为车辆轴距,L2表示相邻车辆下相邻轮对间的距离。本文模型中考虑的4个车轮分别用1、2、3、4表示。在本文的研究频率范围内,可不必考虑车辆二系悬挂系统的影响,故仅建立转向架、一系悬挂、轮对和轮轨接触弹簧的简化车辆模型。

图2 列车-轨道耦合振动模型
由于普通板式轨道和钢弹簧浮置板轨道具有相似的结构特征,两者可采用相同的轨道模型。具体而言,钢轨简化为无限长铁木辛柯梁;扣件用弹簧-阻尼模拟;轨道板简化为有限长欧拉梁;轨道板下的弹性支撑采用弹簧-阻尼模拟。普通板式轨道在轨道板下未设置减振元件,故在计算中将轨道板下的弹性支撑刚度视为无穷大。钢弹簧浮置板下采用钢弹簧离散支撑,需要考虑钢弹簧提供的弹性作用。
轮轨激励来自于车轮和钢轨表面的组合不平顺Δ。本文采用移动不平顺激扰模型,轮轨动态作用力可由动柔度法计算[17-18]
(1)
式中:Fc为轮轨动态作用力,αw、αr分别为车轮、钢轨的动柔度;KH=1/αc,αc为轮轨接触弹簧动柔度;KH为线性化轮轨接触刚度。
本文采用叠加法计算多车轮作用下钢轨的动柔度,以主动轮与从动轮的方法来考虑多车轮之间的相互作用[19]。首先计算主动轮作用处钢轨及轨道板的动柔度系数αri、轨道板上扣件力Fpn和轨道板下支撑弹簧力Fbs;考虑移动不平顺的时间滞后效应,将钢轨动柔度分别代入式(1)中,即可求得4个车轮单独作用下的轮轨动态作用力Fc1、Fc2、Fc3、Fc4,相关计算理论详见文献[19],此处不再赘述。
1.2 箱梁局部振动分析
混凝土箱梁由顶板、翼缘、腹板、底板构成,各板件的局部振动对箱梁的动态特性影响较大,用简单的梁单元模型无法准确反映这种局部振动,因此,本文采用板单元建模。
由“1.1”节可分别得到每一个车轮作为主动轮时各轨道板下支撑弹簧中的力,将其叠加后得到最终作用于箱梁上的激励力,利用通用有限元软件ANSYS进行谐响应分析求解箱梁的振动响应。
1.3 箱梁声辐射分析
采用边界元法求解箱梁结构噪声,将混凝土箱梁外表面记为S,外部声场域记为V。箱梁结构振动响应作为声辐射边界条件时,满足如下表达式

(2)
式中:p为声压;n为S的外法向单位矢量;j为单位虚数;ρ0为空气密度;vn为流体与结构交界面处结构的法向振动速度矢量。箱梁结构表面S上的声压满足亥姆霍兹积分方程和萨默菲尔德辐射条件。
箱梁结构表面S经过划分后,在边界上形成M个单元,N个节点,每个单元的节点数L,设单元上任意位置(x,y,z)的局部坐标为(ξ,η)则

(3)
式中:Nl(ξ,η)为插值形函数。逐次以边界上每个节点为源点,对亥姆霍兹积分方程(P∈S)进行离散,得:
Ap=Bv
(4)
式中:A、B为影响矩阵,与结构形状、尺寸、插值形函数及激励频率有关;p为流体模型表面上节点压力矢量;v为流体模型表面法线方向上节点速度矢量。
p=Zv
(5)
式中:Z=A-1B,为振动结构声阻抗矩阵。
求得p,v后,即可用亥姆霍兹积分方程(P∈V)求得声场中任意一点P的辐射声压
p(P)=aTp+bTv
(6)
式中:a,b为插值函数矢量,与结构表面形状和任意点P的位置有关。
2 算例验证
2.1 工程概况
本文以某城市轨道交通线中的一孔双线30 m简支箱梁为背景,对运营列车作用下的箱梁振动和噪声进行测试。轨道结构形式为普通板式轨道。在箱梁跨中底板中心分别布置加速度传感器和传声器。
图3给出了箱梁跨中截面尺寸和传感器布置图,其中,V1、V2、V3为加速度传感器,代表底板中心、腹板中心、翼板中心的振动测点;S1、S2、S3为传声器,代表底板中心、腹板中心、翼板中心的噪声测点。

图3 箱梁截面尺寸及传感器布置(mm)
2.2 箱梁对钢轨动柔度的影响
由式(1)可知,轮轨动态作用力与车轮、钢轨及轮轨接触弹簧动柔度密切相关。轨道结构布置在箱梁上,因此有必要研究箱梁对钢轨动柔度的影响。
分别采用3种模型计算钢轨动柔度,对比结果见图4。从图4可知,“模型1”为裸箱梁(不设浮置板轨道)的动柔度;“模型2”为浮置板轨道-箱梁模型计算得到的钢轨动柔度;“模型3”为裸浮置板轨道(将箱梁视作刚性基础)计算得到的钢轨动柔度。可以看出:① 在20 Hz以下频段,箱梁动柔度对钢轨动柔度影响较大,5 Hz附近的峰值对应于箱梁的一阶模态;② 在20~200 Hz频率范围内,箱梁动柔度远远小于钢轨动柔度,“模型2”和“模型3”计算得到的钢轨动柔度曲线完全重合。所以,在本文研究频率范围内(20~200 Hz),可将箱梁视为刚性基础,这也说明本文仅考虑列车-轨道耦合是合理的。

图4 钢轨动柔度对比
进一步地,图5给出了车轮、钢轨、轮轨接触弹簧动柔度以及三者之和的频谱曲线图。
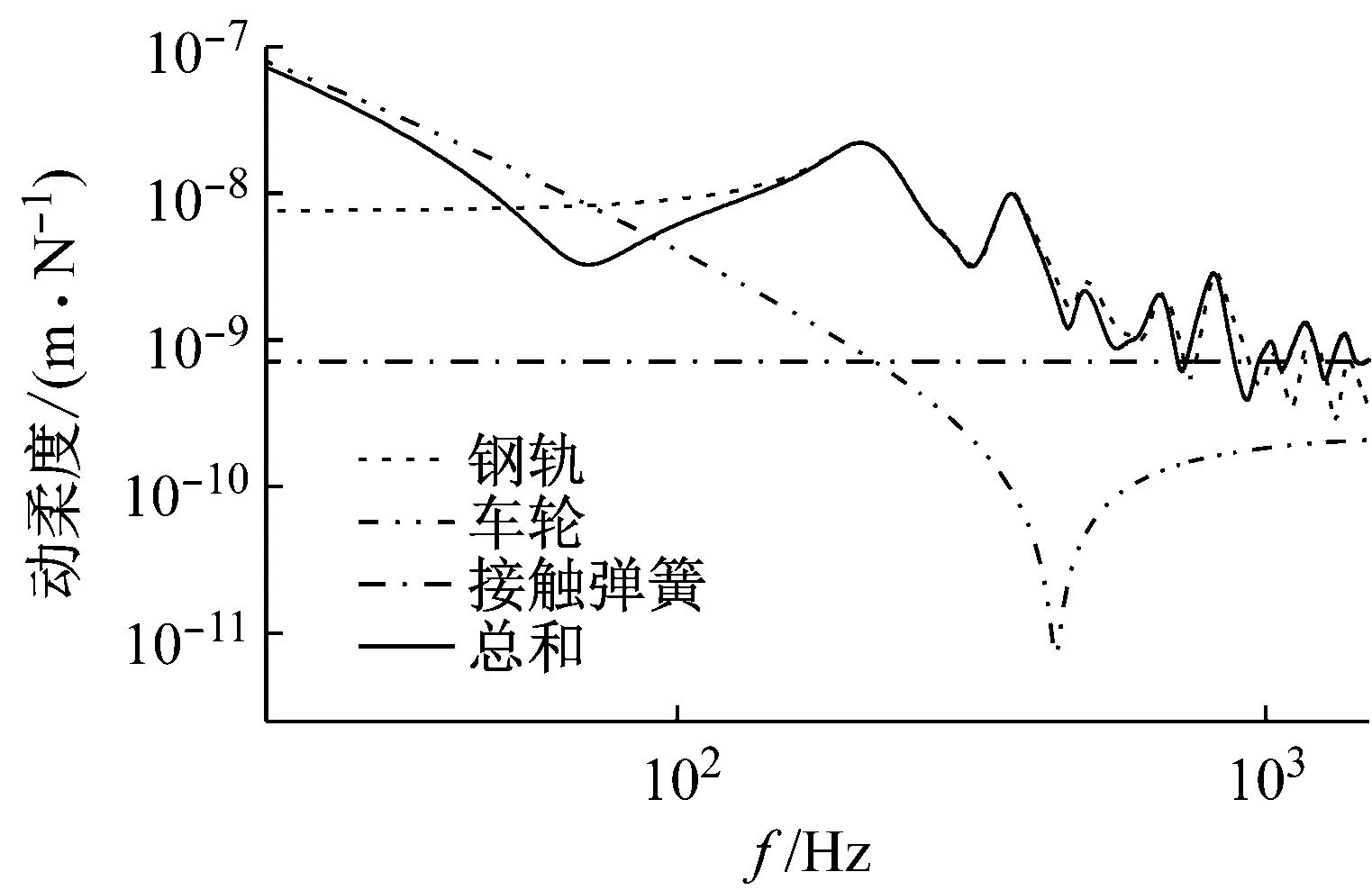
图5 钢轨、车轮、接触弹簧及三者总和动柔度
从图5可知:在40 Hz以下频段,总动柔度主要由车轮动柔度决定;40~100 Hz频段,车轮与钢轨动柔度之和影响总动柔度;100~200 Hz频段,钢轨动柔度起主要作用。
由于在70 Hz附近,车轮与钢轨动柔度幅值相等而相位相反,故总动柔度出现谷值。根据式(1)可知,轮轨动态力与总动柔度成反比关系,故可预见轮轨动态力将在此频率点处出现峰值。
2.3 仿真结果验证
运营列车通过该桥时的车速约为70 km/h,其它计算参数见表1。
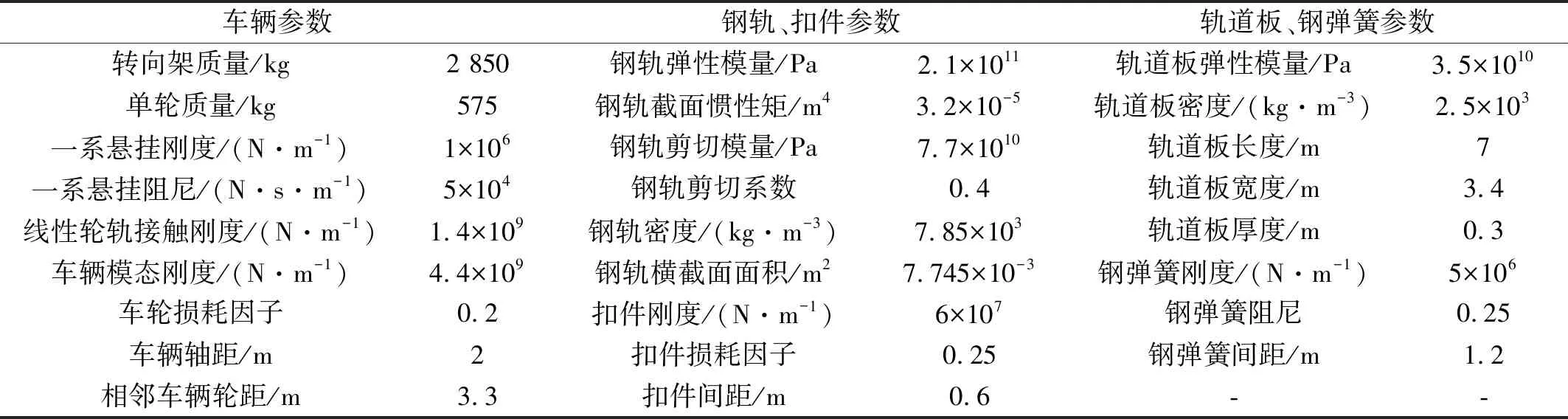
表1 计算参数
由于梁体自身对梁面以上轮轨噪声的遮蔽效应,底板、腹板和翼板附近的实测噪声几乎完全由箱梁的振动引起。图6~图7分别给出了箱梁底板、腹板和翼板的振动加速度级频谱,以及各板件附近的线性声压级频谱,共有4次实测结果。可以看出:① 不论是振动还是噪声,仿真值与实测值总体上均吻合良好,但二者在某些频率处存在偏差,这可能是由于实测结果中包含部分背景噪声的缘故;② 振动和噪声频谱曲线的变化规律比较相似,揭示了振动与噪声存在内在联系;③ 箱梁振动和噪声均在50~125 Hz频率范围内出现较大值,峰值频率均出现在中心频率80 Hz处,其主要原因是列车振动能量主要集中在这个频段内。

(a) 底板中心
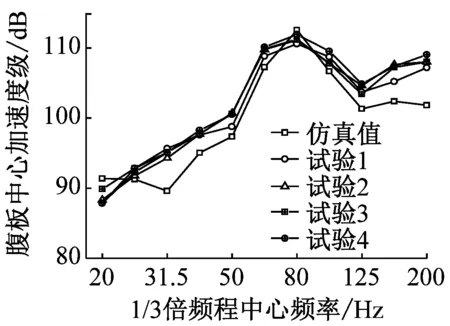
(b) 腹板中心

(c) 翼板中心

(a) 底板中心附近
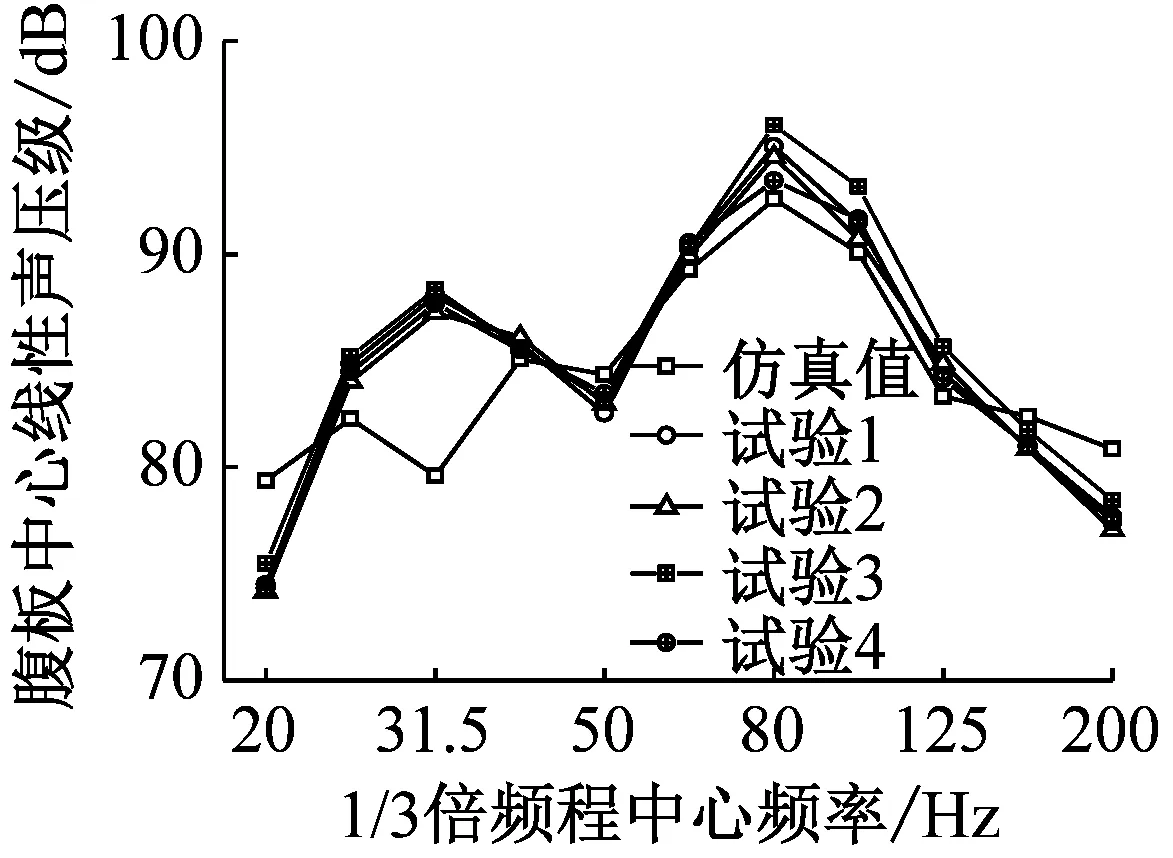
(b) 腹板中心附近
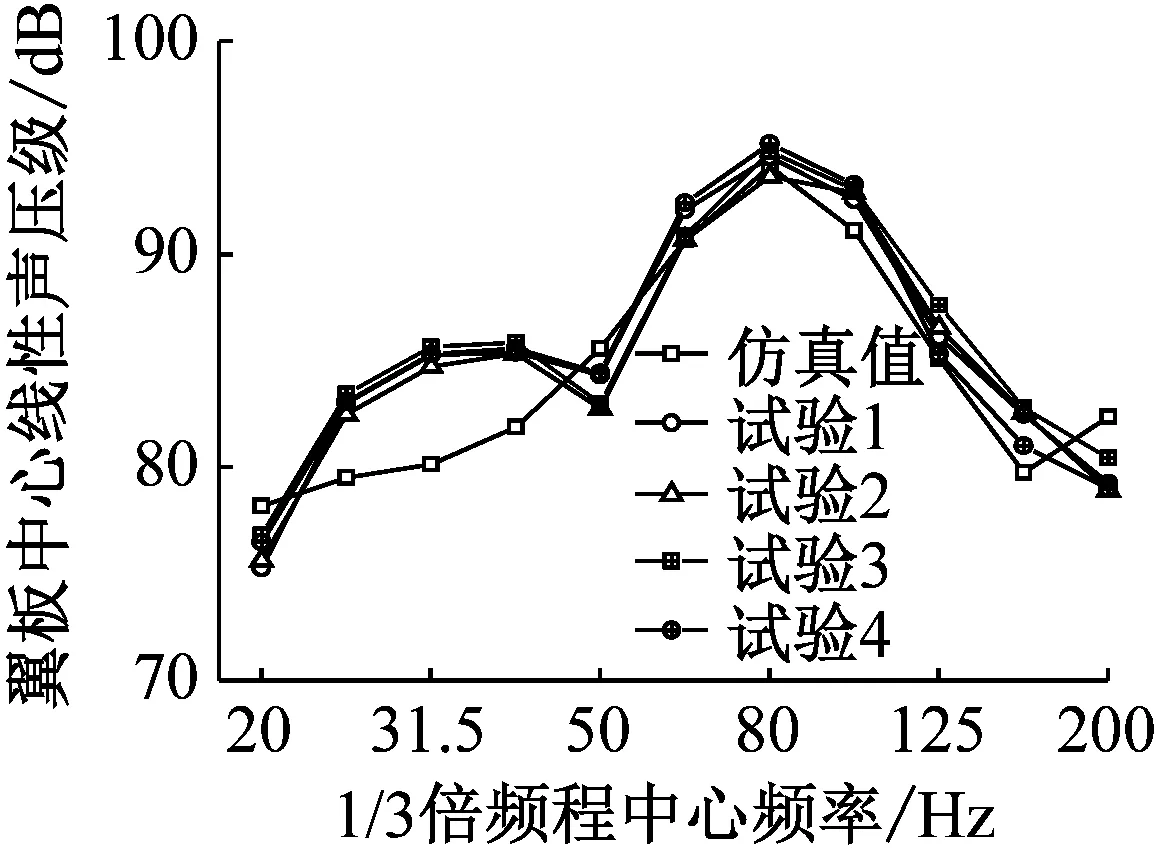
(c) 翼板中心附近
综上所述,本文建立的仿真分析模型可以较好地模拟列车激励引起的箱梁振动和噪声。
3 两种轨道结构的对比
本节采用表1中参数进行仿真分析,对比钢弹簧浮置板轨道和普通板式轨道的影响。
3.1 列车激励
图8给出了两种轨道结构形式下的轮轨力频谱曲线。由图8可知:① 总体上,20~200 Hz频段的轮轨力较大,且在70 Hz附近出现峰值,这与图5的规律一致。超过200 Hz之后,两者轮轨力基本一致,且均有较大波动;② 在20~70 Hz频段,钢弹簧浮置板轨道对应的轮轨力小于板式轨道对应的轮轨力,而70~200 Hz频段的大小关系则相反,这说明轮轨力的频谱特性受到轨道结构参数的影响;③ 在本文所研究的频段范围内,轮轨力的差异原因是两种轨道结构对应的钢轨动柔度有所不同。
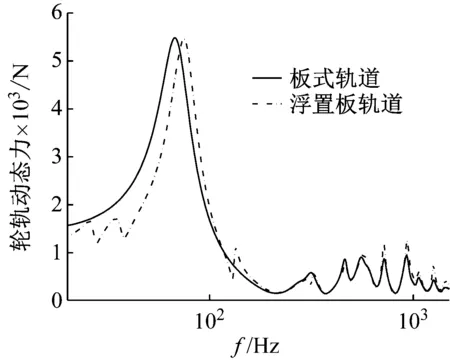
图8 两种轨道结构下的轮轨力
轮轨力经由轨道结构向下传递到箱梁,因而轨道结构形式决定着传递至箱梁的荷载大小。图9给出了两种轨道结构形式下传递到箱梁的荷载。
由图9可知:采用钢弹簧浮置板时,传递到箱梁的荷载明显要小,即浮置板的隔振效果明显。究其原因,这是由于钢弹簧浮置板的力传递率远小于板式轨道,这与相关文献的研究结论一致。

图9 两种轨道结构下传递到箱梁的荷载
3.2 箱梁的声振特性
图10给出了两种轨道结构下箱梁振动加速度级频谱和总振级柱状对比图。图11给出了两种轨道结构下箱梁底板附近的声压级频谱和总声压级柱状对比图。

图10 两种轨道结构下的箱梁振动

图11 两种轨道结构下的箱梁噪声
从图8~图11可知,采用普通板式轨道时,轮轨力、传递到箱梁的荷载、箱梁振动加速度级和声压级均在50~125 Hz频段出现峰值;采用钢弹簧浮置板时,各曲线的频谱特性非常相似,只是对应的峰值频段与普通板式轨道存在一定差异。因此,轨道结构形式决定了传递到箱梁的荷载,进而决定了箱梁振动的频谱特性,并最终决定了箱梁声辐射的频谱特性。
另一方面,两种轨道结构下,箱梁振动加速级和声压级都在80 Hz处出现峰值,而钢弹簧浮置板轨道对应的振动和噪声均要小得多;频率越高,钢弹簧浮置板轨道的减振降噪效果尤为显著;相比普通板式轨道,采用钢弹簧浮置板时,箱梁底板的总振级可减小35.1 dB,箱梁底板附近的总声级可减小24 dB。
综上所述,钢弹簧浮置板对于箱梁振动和噪声均具有极好的控制效果,且减振效果优于降噪效果。
4 钢弹簧浮置板参数的影响
4.1 扣件刚度
分别取扣件刚度KP为30 MN/m,60 MN/m,120 MN/m,240 MN/m,其它参数保持不变,计算得到箱梁底板附近的声压级频谱和总声压级,如图12所示。从图12可知:① 不同扣件刚度下,箱梁噪声频谱曲线均在63~80 Hz处出现峰值。20~80 Hz范围的频谱曲线基本一致。扣件刚度越大,导致传递到箱梁的荷载增大,箱梁噪声就越大,但效果主要集中在80 Hz以后;② 扣件刚度变化时,底板附近的总声压级变化很小,这是由于浮置板轨道有效地隔离了因扣件刚度增大而增加的轮轨力,即在浮置板轨道中采用弹性扣件并不能得到预期的降噪效果。

图12 扣件刚度的影响
相关文献表明:采用弹性扣件会降低轨道衰减率,使振动沿钢轨的传播距离增大,从而增大钢轨噪声,并可能加剧轮轨磨耗。因此,就箱梁减振降噪而言,可在钢弹簧浮置板中采用普通扣件。
4.2 钢弹簧刚度
分别取钢弹簧刚度Kb为5 MN/m、10 MN/m、20 MN/m、40 MN/m,其它参数保持不变,计算得到箱梁底板附近的声压级频谱和总声压级,如图13所示。从图13可知:① 频率较小时(小于25 Hz),由于激振频率比较接近浮置板轨道系统的自振频率,钢弹簧刚度对箱梁噪声的影响规律较复杂;② 频率大于31.5 Hz时,钢弹簧刚度越小,箱梁噪声越小。这是因为在浮置板质量不变的条件下,增加其支承弹性将降低浮置板轨道系统的固有频率,提高其隔振性能,进而实现更好的降噪效果;③ 总体上,钢弹簧刚度每减小一倍,底板附近的总声级可降低5~6 dB。

图13 钢弹簧刚度的影响
降低钢弹簧刚度有利于提高浮置板轨道的隔振性能,减小箱梁噪声。然而,刚度过小的钢弹簧将加剧浮置板和钢轨的振动,增大轨道竖向位移,影响行车平稳性。因此,就箱梁减振降噪而言,可适当放松对钢弹簧刚度的要求,即采用较大的刚度指标。
4.3 浮置板长度
分别取浮置板长度LS为7 m、14 m、28 m、56 m,其它参数保持不变,计算得到箱梁底板附近的声压级频谱和总声压级,如图14所示。

图14 浮置板长度的影响
从图14可知:不同板长下的各条曲线基本重合,即板长对箱梁噪声的影响很小。只有采用极大的板长时(例如56 m),箱梁噪声级才略有减小。
根据隔振原理,增加浮置板长度可以减小其自振频率。但仿真结果显示,20~200 Hz频段范围的箱梁噪声变化不明显,这主要是由于钢弹簧浮置板的自振频率远小于箱梁噪声峰值频率。
4.4 浮置板厚度
分别取浮置板厚度tS为0.3 m、0.4 m、0.5 m、0.6 m,其它参数保持不变,计算得到箱梁底板附近的声压级频谱和总声压级,如图15所示。从图15可知:① 总体上,不同厚度条件下,箱梁噪声频谱曲线变化规律相似。频率小于80 Hz时,浮置板厚度越大,箱梁噪声越小。超过80 Hz后,厚度变化对箱梁声压级影响较为复杂;② 浮置板厚度每增加0.1 m,箱梁底板附近总声压级降低1~3 dB。当厚度从0.3 m增加到0.4 m时,总声压级降低最多,达到3 dB。

图15 浮置板厚度的影响
增加浮置板厚度可在一定程度上提高其隔振性能,减小箱梁噪声,但由此造成桥梁二期恒载急剧增加。考虑到钢弹簧刚度对箱梁噪声的影响更明显,建议在实际工程中可适当选取较薄的板厚。
5 结 论
本文建立了列车-轨道耦合振动频域解析模型获得传递至箱梁的荷载,再借助有限元法进行振动响应分析,最后采用边界元法分析箱梁噪声。以某城市轨道交通线中的30 m简支箱梁开展现场测试,以验证模型的可靠性。基于此模型,对比了普通板式轨道和钢弹簧浮置板两种轨道结构形式对箱梁振动声辐射的影响。进一步地,讨论了钢弹簧浮置板参数对箱梁噪声的影响。主要结论如下:
(1) 在200 Hz范围内,两种轨道结构下的轮轨力相差不大,但采用钢弹簧浮置板轨道时,传递到箱梁上的荷载远小于采用普通板式轨道的结果。
(2) 相比普通板式轨道,采用钢弹簧浮置板时,箱梁底板的总振级可减小35.1 dB,箱梁底板附近的总声级可减小24 dB。
(3) 影响箱梁噪声的主要因素是钢弹簧刚度,其次是浮置板厚度。钢弹簧刚度每减小一倍,底板附近的总声级可降低5~6 dB。浮置板厚度每增加0.1 m,降噪量提高1~3 dB。
(4) 扣件刚度及浮置板长度对箱梁噪声的影响很小。在钢弹簧浮置板轨道中,可采用普通扣件而不必选择弹性扣件。对于浮置板长度,应根据其它因素确定。

