爆炸螺栓冲击响应的主要影响因素研究

王军评， 毛勇建， 吕 剑， 黄含军

(中国工程物理研究院 总体工程研究所，四川 绵阳 621900)

爆炸分离冲击(也称爆炸冲击、烟火冲击，等)是指航天器为完成级间分离、星箭分离、设备驱动等功能采用的火工装置动作后，由于高频、高量级的应力波传播而产生的强作用的瞬态冲击载荷[1-2]。这种短时、高频、高幅值的冲击载荷对航天器结构特别是电子系统、光学元器件、脆性材料具有较强的破坏损伤效应[3-4]，严重时会导致任务失败等灾难性事故。因此，为了深入认识该问题，国内外在爆炸分离冲击载荷作用机理及传递规律、响应预示与数值分析[5-12]、模拟试验技术[13]等方面开展大量的工作。

爆炸螺栓由于结构简单易于安装等优点在航天工程中广泛应用。其动作时产生的冲击载荷由含能材料爆炸、螺栓断裂使预紧力释放以及螺栓头撞击结构特定部位形成应力波及谐振效应三部分组成。这三种载荷作用机理及力学效应在相关文献中已有介绍。如，王军评等通过分别建立三种独立的解耦数值模型，对三种载荷的作用机理进行了初步的探索；黄含军等[14]通过试验研究了两种预紧力的单因素变化对响应的影响；张建华从定性的角度指出应变能的突然释放增加了爆炸冲击环境的烈度。上述工作分别从独立的、单一的、定性的角度研究了爆炸分离冲击载荷及其对结构的影响，而爆炸螺栓在实际动作的物理过程中[15]，特别是含能材料的爆炸和预紧力释放几乎发生在同一时段内，二者之间必然会相互影响、相互耦合。但遗憾的是，至今仍缺乏对爆炸解锁的全过程、多因素耦合数值分析技术的研究以及耦合效应下各主要因素(如药量、预紧力、撞击部位材料)的变化对结构响应影响的系统分析。

爆炸螺栓动作时，其物理过程在时序上可以划分为两阶段:第一阶段为含能材料的爆炸使螺栓解锁，本阶段形成的载荷包含两部分，一部分为炸药爆炸使化学能释放形成冲击载荷，另一部分为螺栓断裂，使预紧力产生的应变能释放，这两部分所形成的载荷在实际的物理过程中几乎是同步发生的，二者相互影响、相互耦合；第二阶段为螺柱以一定的速度撞击结构的特定部位。本文针对上述问题，以典型爆炸螺栓连接结构为对象，分别建立预紧状态下爆炸螺栓爆炸解锁过程及撞击过程的数值模型，分析了耦合效应下炸药量、预紧力、撞击部位材料等的变化对结构响应的影响。可为地面模拟试验设计、结果评估、预示方法的选择及爆炸冲击防护装置与缓冲设计提供参考。

1 数值计算模型与方法

1.1 预紧状态下螺栓爆炸解锁过程的数值模型及计算方法

在数值计算时，针对爆炸螺栓连接结构，在LS-DYNA中，通过动力松弛直接给螺栓加载预紧力，并采用重启动技术，建立了预紧状态下爆炸螺栓爆炸解锁过程的耦合数值模拟模型。

1.1.1 爆炸螺栓连接结构的数值模型

计算模型参考文献[5]的外形结构，由六只爆炸螺栓连接的锥壳上、下件。单位采用g-cm-μs(克-厘米-微秒)。根据对称性，建立1/12模型，并施加对称边界如图1所示。其中，炸药和周围空气采用ALE网格建模，炸药用LS-DYNA中的High Explosive Burn模型描述，其爆轰产物的压力用JWL状态方程描述，具体参数见表1。空气用多项式状态方程描述，参数见表2。爆炸螺栓与锥壳采用Largrange网格建模，锥壳及爆炸螺栓用线弹性本构描述，锥壳为铝质材料，弹性模量为70 GPa，密度为2.7 g/cm3，爆炸螺栓材料为钢，弹性模量为200 GPa，密度为7.83 g/cm3，剪切销用随动塑性Cowper-Symonds本构描述，材料为铜，具体参数见表3。

图1 有限元模型

表1 炸药材料参数

表2 空气材料参数

表3 铜的参数

1.1.2 预紧力的施加方法

要模拟预紧状态下爆炸螺栓连接结构的爆炸解锁过程，首先需要对爆炸螺栓加载预紧力。螺栓预紧状态下，螺柱受拉，被连接件的接触面受压，螺柱危险截面的所受的拉应力最大。螺柱所施加的预紧力F=M/0.2D，其中M为拧紧力矩，D为螺柱的直径。

定义螺柱危险段的中间位置为加载面(见图2)，通过预紧力和危险截面面积得到的截面预应力定义具有时间历程的加载曲线，然后通过动力松弛使应力重新分配，即可完成对螺栓预紧力的直接加载。以80 N·m拧紧力矩为例，计算得到的应力分布如图3所示。从图3可知，销钉及其周边位置的应力最大，螺柱的危险区域次之；从轴向应力分布可知，螺栓受拉，被连接件、螺母及外套与被连接件接触的位置受压；应力分布符合实际情况，危险截面段的应力值与理论值吻合较好。

1.1.3 预紧状态下爆炸螺栓爆炸解锁过程数值模拟方法

按照前文预紧力加载方法计算，至550 μs(即预紧加载后应力重新分配及平衡基本完成时，已达到收敛)停机，然后采用重启动技术，重新定义炸药的材料及起爆点的位置和时刻，并对爆炸螺栓及锥壳的上、下件进行应力初始化，继续计算至1.55 ms，完成预紧状态下爆炸解锁全物理过程的数值模拟。

为对比分析药量变化对爆炸分离冲击响应的影响，建立了与标准药量相比，比例为0.75、1.00、1.25、1.50、1.75五种药量的数值模型，图4给出了0.75及1.00倍的药量的数值模型，通过上述方法分别对80 N·m下五种药量的螺栓解锁过程进行计算。

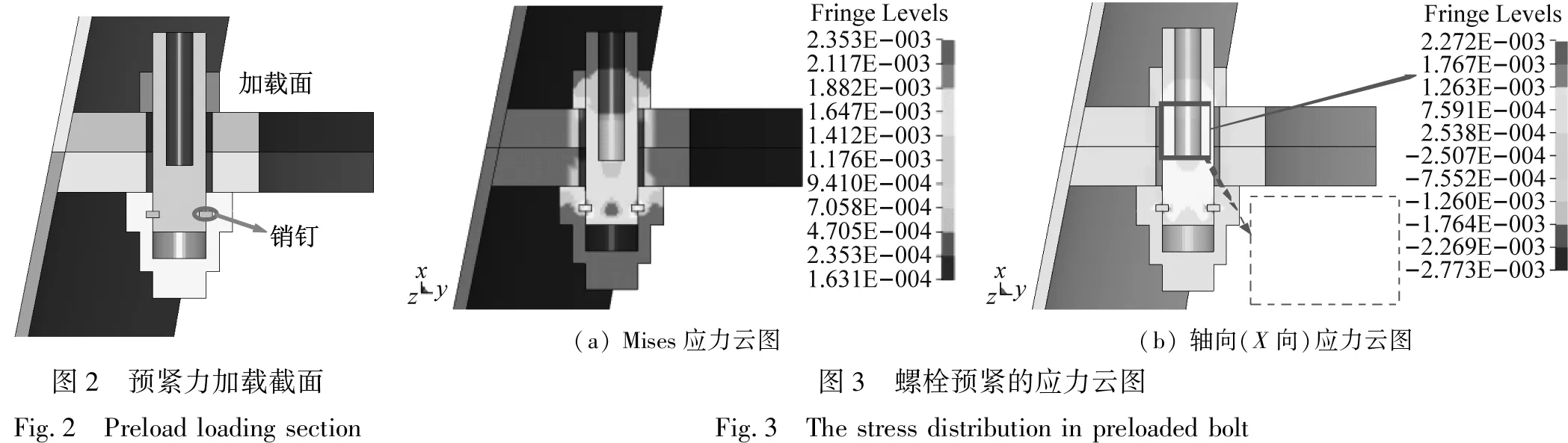
(a) Mises应力云图(b) 轴向(X向)应力云图图2 预紧力加载截面Fig.2 Preload loading section图3 螺栓预紧的应力云图Fig.3 The stress distribution in preloaded bolt

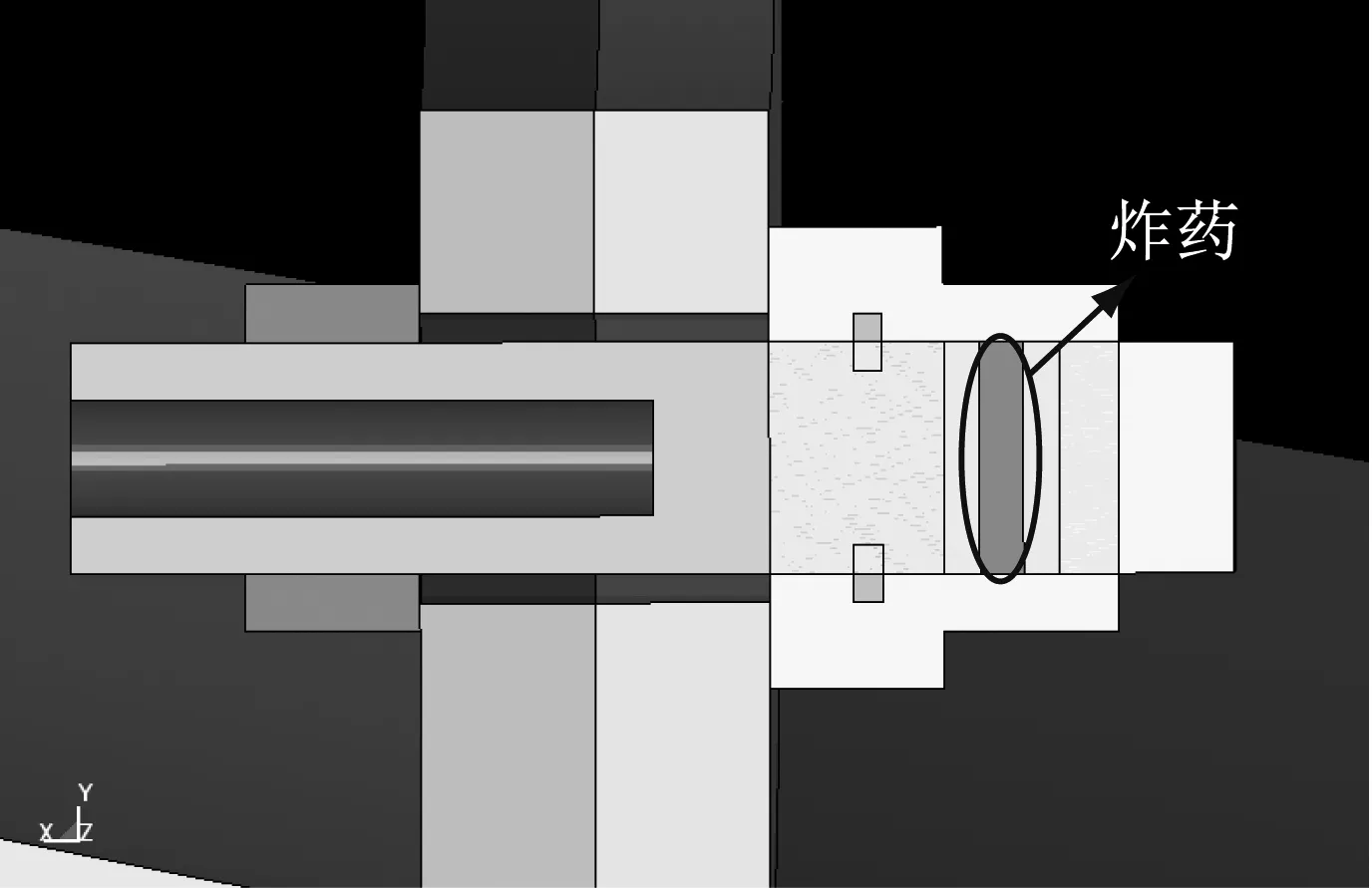
(a) 0.75倍

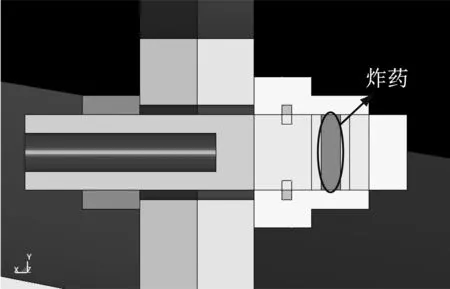
(b) 1.00倍

为分析预紧力变化对爆炸分离冲击响应的影响，以标准药量的模型为对象，分别对20 N·m、40 N·m、60 N·m、80 N·m、100 N·m、120 N·m、140 N·m的工况进行数值计算。

1.2 不同的缓冲材料撞击模型

在爆炸螺栓动作的第二阶段。即，螺柱以一定的速度撞击结构的特定部位。撞击部位的结构形式和材料的性能是影响结构响应的关键因素，本研究主要分析撞击部位不同的材料对冲击响应的影响。在上文模型的基础上，仅建立锥壳上件、螺柱和螺母，模拟螺柱与特定部位撞击(简化为挡板)的过程。挡板分别采用铝材(2Al2)、RB-55真空橡胶、FM-32海绵橡胶、泡沫铝。其中，铝采用随动本构描述；真空橡胶用不可压缩Ogden模型描述，FM-32橡胶为用可压缩Ogden模型描述，材料参数见表4[16]；泡沫铝用可压缩性泡沫材料模型[17]，主要参数见表5[18]。

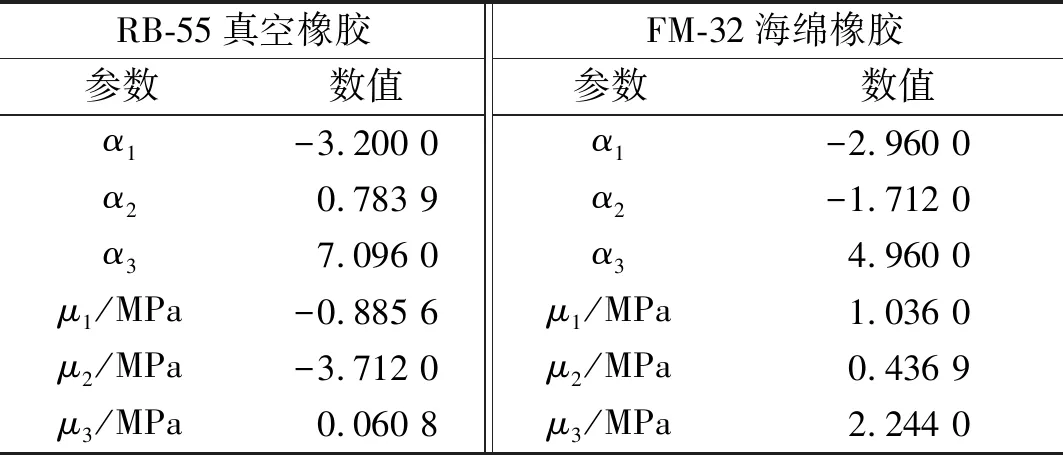
表4 两种橡胶材料的Ogden本构模型参数

表5 泡沫铝的参数

2 结果与分析

2.1 药量变化

图5给出了五种不同比例药量的结构在分离装置动作后，同一时刻(起爆后121 μs)的螺栓的位置。由图5可知：在t=121 μs时药量比例为0.75的爆炸螺栓其剪切销在高压气体的作用下刚被剪断，已基本完成解锁；而药量为1.00的结构，其销钉早已断裂，螺柱与螺母的相对行程明显比药量为0.75的大；可见随着药量的增大，螺栓的解锁时间减小，螺柱和螺母的相对行程增大，分离装置内的应力增高。1.25倍、1.50倍及1.75倍药量下螺栓的行程及应力云图表现出相同的趋势。

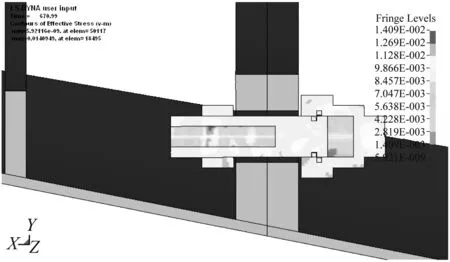
(a) 0.75倍

(b) 1.00倍

图6(a)给出了药室中心五种不同比例药量压力峰值的对比，在炸药的中心位置，对比不同药量的压力峰值，可知随着药量的增大，压力峰值增大；图6(b)给出了五种不同比例药量在药室的边缘(距炸药中心0.44 cm)压力曲线，其压力峰值也随药量的增大而增大，结合图5可知，解锁时间与压力幅值紧密相关，幅值越大解锁时间越短。

图7给出了标准药量(比例为1)连接结构距冲击源分别4.5 cm、16.0 cm、123.0 cm的三个典型位置(按NASA-STD-7003可认为三个点分别位于近场、中场、远场)的轴向加速度时域响应曲线。由图7可见，在爆炸分离冲击载荷的激励下，近场区域的幅值高达12 000 g，高频达200 kHz左右，中场区域的幅值约为1 800 g，频率达25 kHz，远场区域的幅值约为400 g，大多数频率成分小于10 kHz。对比近、中、远场，可发现幅值和频率衰减很快，这是由于爆炸和应变能释放主要表现为应力波传播效应，因此随距离的增加幅值和频率衰减剧烈。

(a) 炸药中心

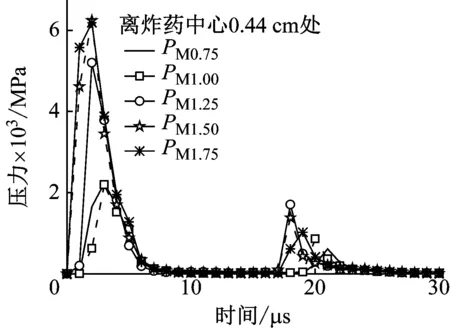
(b) 药室边缘

Fig.6 Comparison of the pressure at explosive center, chamber edge of five different weights of explosives

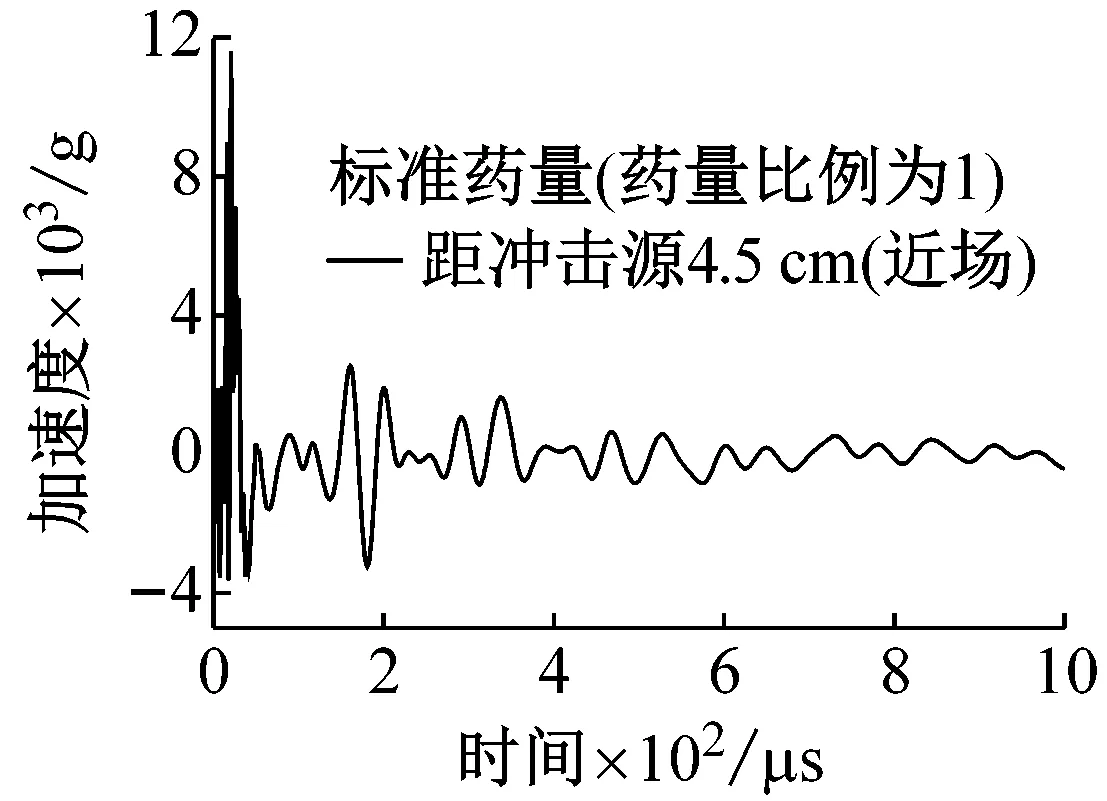
(a) 距冲击源4.5 cm

(b) 距冲击源16.0 cm

(c) 距冲击源123.0 cm

图8给出不同药量下三个典型位置的冲击响应谱。由图8可知，近场区域(见图8(a))在100 kHz以上有很高的谱分量，频域峰值加速度高达104g，响应具有明显的高频特性；中场区域(见图8(b))在20 kHz以上有较高的谱分量，幅值较大，50 kHz开始迅速衰减；远场区域(见图8(c))谱分量大多数分布在小于等于20 kHz区域，频域峰值与中场比明显减小。对比药量比例为1.00频谱峰值，其幅值从距冲击源4.5 cm(近场)的33 818g，至距冲击源16 cm(中场)衰减为4 450g，到距冲击源123 cm(远场)的1 101g，对应的频率从200 kHz衰减至约10 kHz。可见，在频域上峰值及频率表现出较强的随到冲击源增加而迅速衰减的规律，与时域相同。不同药量下，同一位置的响应在频域下，其整体趋势和波形基本一致，在较宽频段内(近场：103～106Hz，中、远场：102～104Hz)，其幅值随药量的增加而增大，但并不成比例递增。

图9给出了不同药量的结构时域加速度响应峰-峰值(见图9(a))及频域加速度峰值(见图9(b))随距离的传递趋势。由图9可知，不同药量的结构，时域和频域加速度峰值随距离的传递规律具有一致性，在靠近冲击源20 cm以内，加速度响应衰减非常剧烈；但从20 cm至锥壳小端的较长距离内，加速度峰值衰减缓慢。此外，图9还清楚地显示了加速度响应衰减的另一个特点：在距离40～60 cm，响应衰减曲线出现一个峰值，明显高于前后观测点，随距离的增加，峰值呈现非单调递减的情况。分析认为，这是由结构特性造成的。在此范围内，结构刚度较强，造成了较大的加速度响应(在类似试验中也存在此种现象)。因此可以认为，本文的结构对爆炸分离冲击响应的衰减呈现非单调的特性。

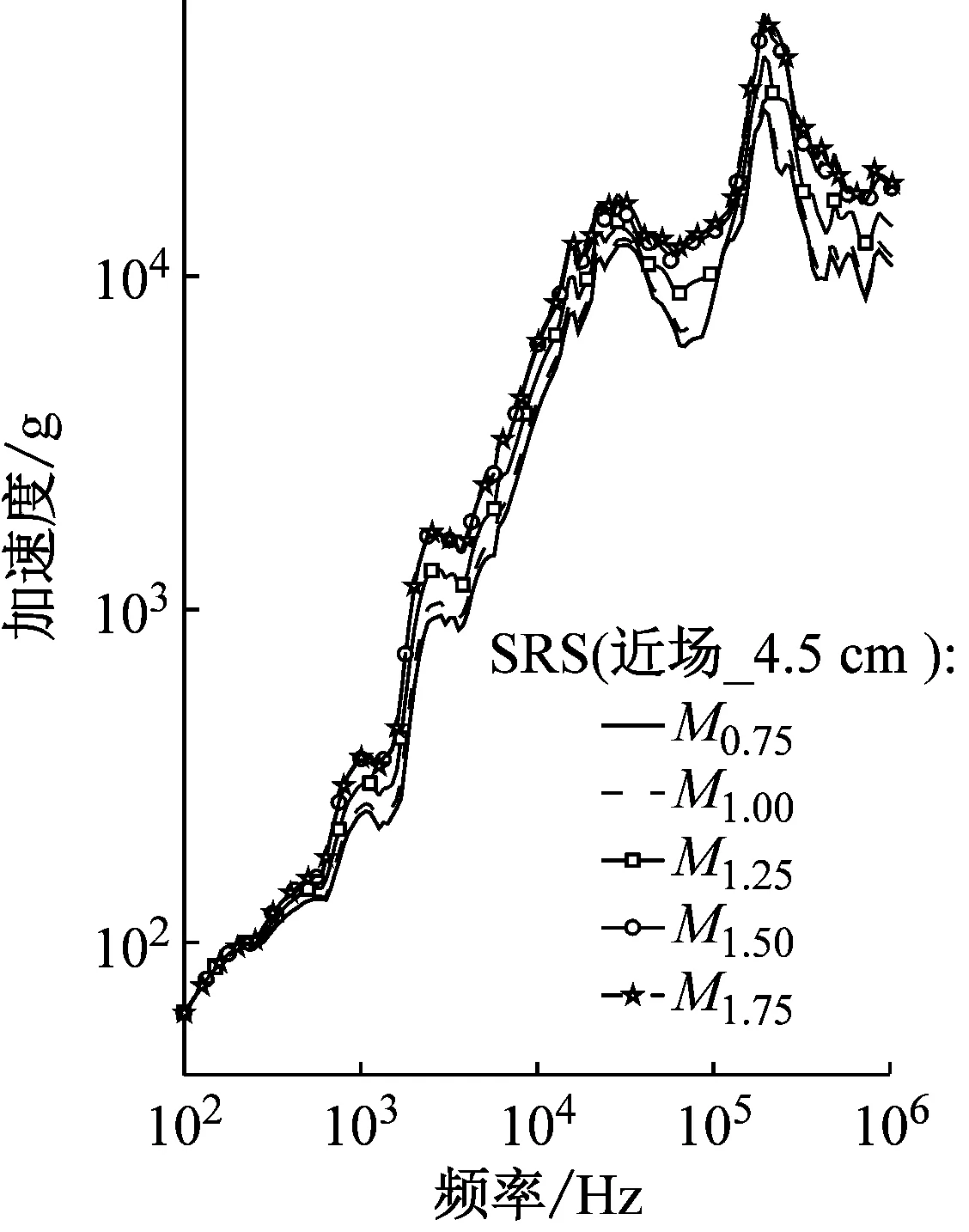
(a) 距冲击源4.5 cm

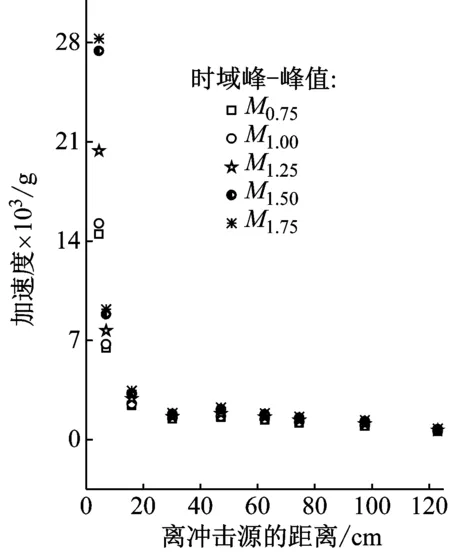
(a) 时域

(b) 频域

这是由于爆炸分离冲击是一个非常复杂的过程，产生的载荷也非常复杂。在此载荷作用下，结构响应在不同阶段和不同区域表现为不同的物理机制。在近场区域(根据NASA-STD-7003，对强冲击源，d≤15 cm的区域为近场，60 cm≥d15 cm为中场)，主要受到应力波传播控制，响应具有明显的高频特性，随时间和与冲击源距离的增加衰减非常剧烈，在宏观距离上看，即使是距离相同的测点，受具体结构细节和距离的细微差异影响，其加速度峰值的分散性也比较明显。在中场区域，受应力波传播和结构谐振双重控制，响应呈现宽频带特点。随着距离的增加，应力波效应逐渐减少，因此响应幅值和频率都呈下降趋势，最终表现为结构谐振效应。但在中场区域内，具体位置的响应频率和幅值受与冲击源距离以及局部结构特性的影响明显，因此传递规律不在是简单的单调函数，而可能因结构特性的不同在某距离范围内呈现峰值。

图10给出了结构响应峰-峰值的比值(与药量为0.75的响应峰值相比)随药量变化的趋势。由图10可知，对于同一位置，响应峰值的比值随药量的增大而增大，但增大的程度与到冲击源的距离有关，主要表现为随距离的增加其比值基本呈现递增趋势变缓和梯度变小的现象。说明结构响应对药量变化的敏感程度与距冲击源的距离相关;近场的响应对药量的变化最敏感，远场结构响应的影响最小。

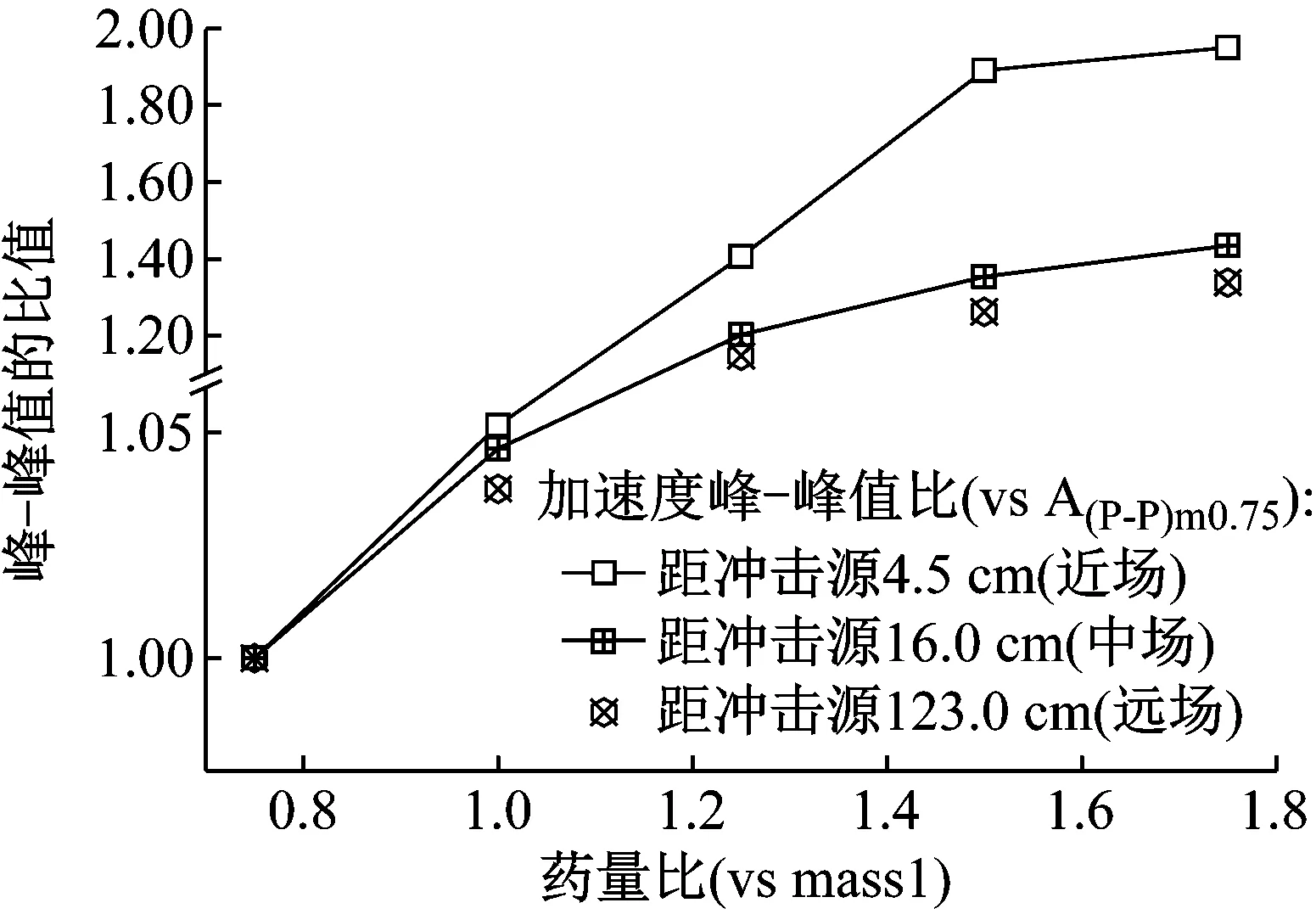
图10 结构响应峰-峰值的比值随药量的变化

2.2 预紧力变化

图11(a)给出了典型位置加速度峰-峰值随预紧力变化的趋势，图11(b)给出了典型位置结构响应峰-峰值的比值(相对于预紧力为80 N·m的峰-峰值)随预紧力比值(相对于80 N·m)的变化情况。由图11(a)可知，随着预紧力的增加，近场、中场、远场的响应峰值的递增程度各有区别，中、远场的呈现线性递增的趋势；而在近场，预紧力较小时(20 N·m和40 N·m)，越靠近冲击源由于爆炸载荷的影响占据主导性，预紧力在此范围内变化，对响应峰值的影响较小，但随着预紧力的逐渐增大，加速度响应峰-峰值也呈现出线性递增的趋势。

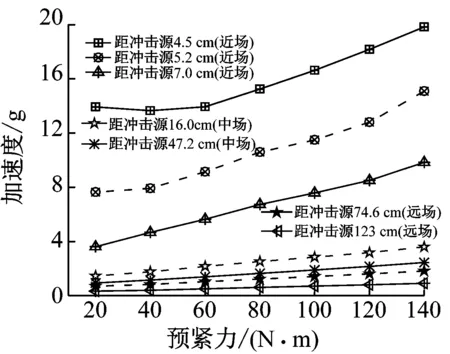
(a)

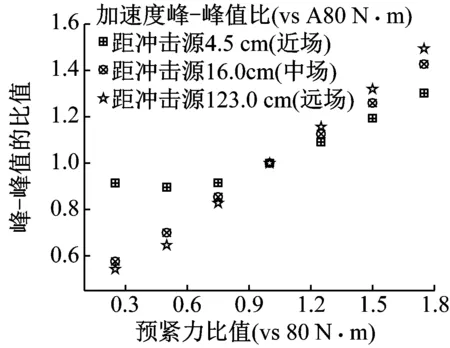
(b)

从整体趋势上看(见图11(b))，各特征位置加速度峰值比随预紧力基本呈现出单调递增的特点，随到冲击源距离的增加，其递增的梯度增大，近场的梯度最小，远场最大，从增量来说远场的响应对预紧力更敏感，但由于远场的加速度幅值基数较小，所以即使增长比例大，其增加后的峰值相对近场还是小量。

2.3 耦合效应下药量和预紧力变化对结构响应影响的对比分析

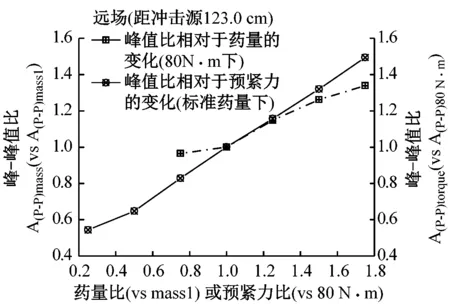
为了对比分析耦合效应下药量和预紧力变化对结构响应的影响，图12给出了三个典型位置的响应峰-峰值比(相对于标准药量、预紧力为80 N·m的加速度响应),在80 N·m下随药量和标准药量下随预紧力变化的对比。从图12可知，横坐标为力矩(相对于80 N·m)或药量(相对于标准药量)的比值，左纵坐标为结构在同一预紧力(80 N·m)下,不同药量模型的加速度峰-峰值与标准药量的加速度峰-峰值之比;右纵坐标为同一药量(标准药量)下,结构在各预紧力的加速度峰-峰值与80 N·m的响应峰-峰值之比。

(a) 距冲击源4.5 cm

(b) 距冲击源16.0 cm

(c) 距冲击源123.0 cm

图12 结构响应峰值比随药量和预紧力变化的对比

Fig.12 Acceleration peak-peak ratios varying with weights of explosives and pretension force

在近场区域(见图12(a))，加速度峰值比随药量比的变化呈现非线性递增的趋势，随预紧力比值基本呈线性递增；药量与预紧力同比值变化时，加速度峰值比的增量受药量的影响大，峰值比最大差别达到了0.55，这说明药量的变化对近场的加速度响应具有主导作用。

在中场区域(见图12(b))，加速度峰值比随药量比也呈现非线性递增的趋势，但其整体的增长梯度相比近场在减缓，峰值比随预紧力比值也呈线性变化但相对于近场其斜率在增大。药量与预紧力同比值变化时，加速度峰值比的增量在药量和预紧力的比值在0.75～1.75变化时由药量主导，在比值为1.75时，峰值比出现了交叉，这说明在中场区域的结构响应受药量和预紧力的双重控制，在药量和预紧力变化较小时，受药量主导，变化较大时，由预紧力主导。

远场区域(见图12(c))，峰值比随药量比和预紧力比的变化趋势与近、中场相似，呈现非线性和线性递增的规律，但峰值比随药量比的增长梯度是三个区域中最小的，而随预紧力比变化的斜率是三区域中最大的。由图12(c)可知，药量与预紧力同比值变化时，除了比值为0.75时，其余位置的峰值比受预紧力影响大，这说明预紧力的变化对远场区域的加速度响应具有主导作用。

2.4 撞击部位材料的变化对冲击响应的影响分析

图13给出了螺柱撞击作用下，撞击部位为不同材料时(2Al2、真空橡胶、海绵橡胶和泡沫铝)，撞击位置的变形曲线。由图13可知，挡板材料为铝(2Al2)时，其变形最小，基本在弹性范围内变化；真空橡胶挡板在撞击后，产生较大的弹性变形，随后回弹并恒定，其塑性变形为0.09 cm；海绵橡胶挡板在达到最大变形，回弹后塑性变形量为0.46 cm；泡沫铝在达到最大变形后，无回弹现象，塑性变形为1.27 cm。

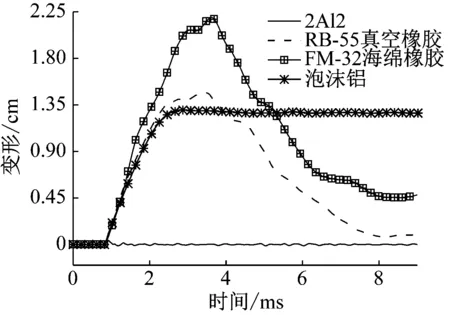
图13 撞击部位的变形

图14给出了不同材料的总能量曲线。由图14可知，在冲击载荷作用下，除泡沫铝外，其它三种材料的总能量在达到最大值后都有一定的回弹，经过震荡后基本稳定于恒值，这是由于其变形量中弹性成分较大，初期动能在总能量中占比较高，随着时间的推移，动能慢慢的衰减耗散；而泡沫铝由于屈服强度较小，在冲击载荷的作用下，泡沫材料被迅速压实，其能量基本全部转化为内能，表现出较好的吸能效果，结合图13可知，四种不同的材料的挡板，泡沫铝的吸能性能最好，海绵橡胶要略优于真空橡胶，2Al2最差。

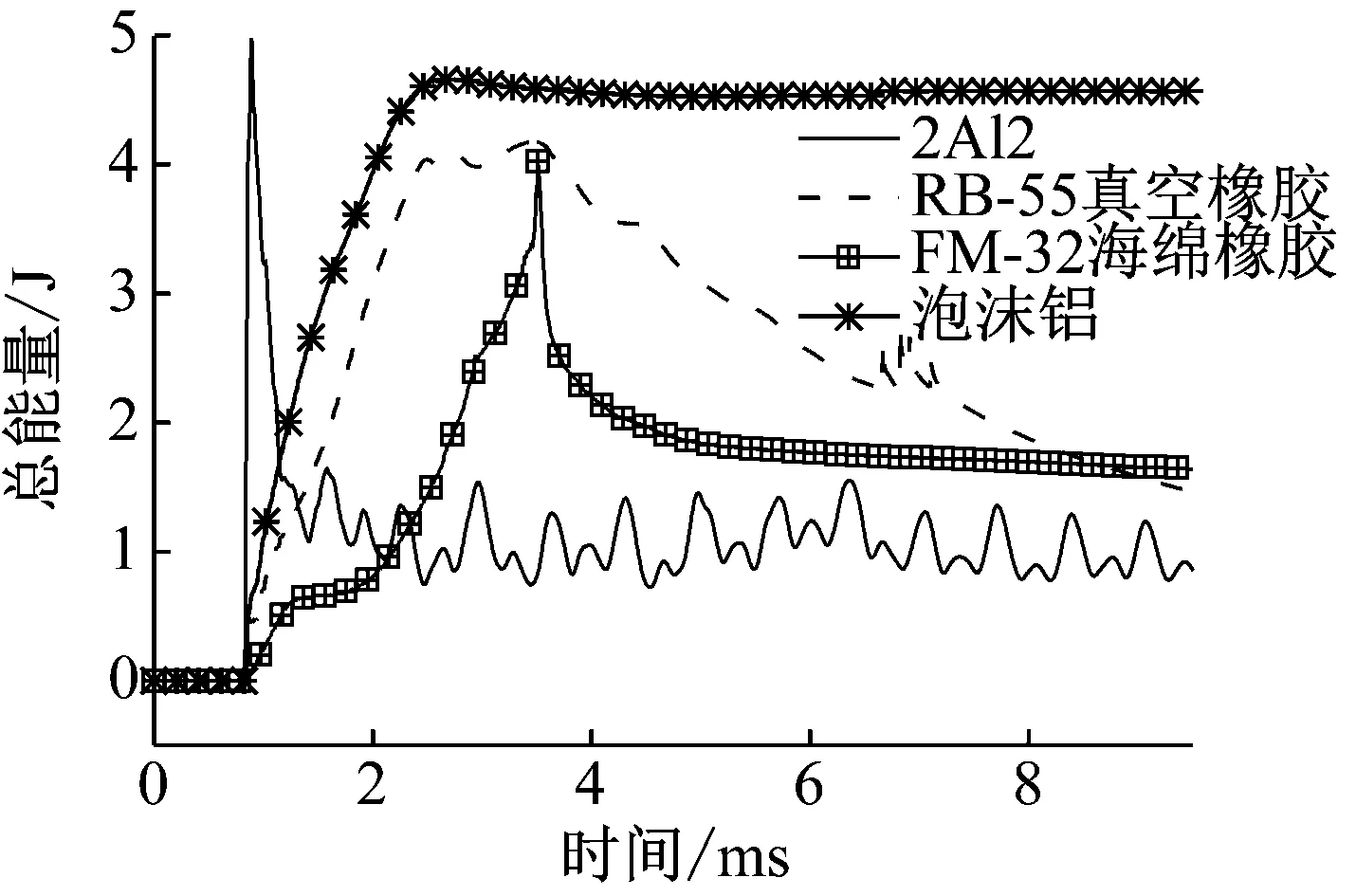
图14 不同材料挡板的总能量

图15给出了在螺柱撞击作用下，撞击部位为不同材料时，近场区域特征点的加速度峰-峰值对比图。由图15可知，挡板材料为2Al2时，观测点的响应最大，其峰峰值为6 961.7g；材料为真空橡胶时，响应其次，峰峰值为382.9g，再次为泡沫橡胶，峰峰值为324.1g；泡沫铝，加速度响应最小，峰峰值为142.8。真空橡胶、海绵橡胶和泡沫铝材料，同一位置加速度响应相对于铝减小一个量级，非常显著。这三种材料相对于铝都具有较好的吸能特性，但略有差异。具体表现为泡沫铝最优，说明泡沫铝能极大的阻碍冲击载荷在结构中的传播；海绵橡胶要略好于真空橡胶，这与挡板的塑性变形和总能量的趋势一致。从加速度响应量级上看，除铝外，其余三种材料的吸能效果基本在一个量级，差异较小，在实际的试验中，可以考虑选用真空和海绵橡胶的组合方式来替代泡沫铝,减小试验成本。

图15 加速度峰值的对比

3 结 论

本研究以爆炸螺栓连接结构为对象，从火工装置工作的实际物理过程出发，把爆炸螺栓动作过程在时序上划分为爆炸解锁和撞击两阶段，分别建立了预紧状态下爆炸螺栓爆炸解锁过程和撞击过程的数值模型，综合数值模拟结果，爆炸分离冲击载荷各主要因素对结构响应的影响表现为：

(1) 在爆炸解锁阶段。从数值分析的结果可知，近场区域，冲击响应随药量呈非线性递增的趋势，随预紧力呈线性递增，药量和预紧力同比值变化时，加速度峰值比的增量受药量的影响大；峰值比最大差别达到了0.55，说明药量的变化对近场的加速度响应具有主导作用。在中场区域，响应峰值随药量也呈现非线性递增的趋势，但其整体的递增梯度相比近场减缓；随预紧力也呈线性变化但相对于近场其斜率增大；在药量和预紧力变化小于1.75，响应受药量主导，变化大于1.75时，由预紧力主导。远场区域，响应随药量和预紧力的变化与近、中场相似，呈现非线性和线性递增的规律；但其峰值随药量的增长梯度是三个区域中最小的，而随预紧力变化的斜率是三个区域中最大的；预紧力的变化对远场区域的响应具主导地位。

(2) 在螺柱撞击阶段。对于撞击部位材料的变化，结果表明，结构响应与撞击部位的材料特性紧密相关，具有较小屈服强度和较大塑性变形能力的材料，吸能效果较好，撞击激发的结构响应较小。

本文从定量的角度综合分析了耦合效应下三种因素对结构响应的影响，从结果和预示方法两个层面，为爆炸分离冲击载荷的作用机理和结构响应的传递规律的理解,提供了有益的参考。