考虑纵坡影响的曲线梁桥地震碰撞响应试验研究

李娜娜, 许维炳, 陈彦江, 闫维明, 苏 鹏

(北京工业大学 建筑工程学院， 北京 100124)

曲线桥具有优越的空间、地形适应能力，是高等级公路、城市立交桥、城市高架桥、山区道路等交通工程中的常见桥型。然而由于曲率半径的影响，曲线桥弯扭耦合作用明显。与直桥相比，地震作用下曲线桥更容易发生损伤或破坏[1-2]。同时由于曲率半径的影响，曲线桥在地震荷载下极易发生碰撞(存在显著的内外侧变形差)，曲线桥的震损也存在明显的碰撞诱发性：① 曲线桥的上部结构更容易发生落梁或碰撞破坏，地震响应分析时，主梁和桥面系的震损不容忽视；② 碰撞会加剧墩柱、桥台、支座等桥梁下部构件地震破坏的可能性。

为明晰碰撞效应对桥梁结构抗震性能影响，国内外学者针对桥梁碰撞效应及碰撞影响开展了系列研究。数值模拟方面，Praveen等[3]研究了共轴直杆模型结构的碰撞机理及过程中的能量耗散机制；Tsai[4]利用接触单元法研究了主梁刚度及伸缩缝宽度对结构碰撞响应的影响；王军文等[5-6]将直杆共轴碰撞模型和Kelvin模型等用于非规则桥梁的碰撞分析当中，推荐了非规则梁桥纵向、横向碰撞的数值模拟方法；吴璟[7]研究了曲杆轴心碰撞理论，由于其仅考虑了曲杆沿杆端平动的情况，其结论说明可采用Kelvin模型分析曲线梁的梁端碰撞，但其碰撞刚度应修正为较短主梁的轴向刚度；彭天波等[8]利用局部集中质量接触单元法，研究了其在梁式桥梁体与桥台碰撞问题模拟中的应用；王东升等[9]研究了主梁之间碰撞刚度的取值建议和碰撞能量损耗随阻尼的变化规律；何健等[10]分析了碰撞刚度对三跨连续斜交桥的影响；李忠献等[11]结合Hertz碰撞模型推导了Kelvin模型中碰撞刚度的计算表达式，但其刚度的计算结果有赖于Hertz模型碰撞刚度的取值；高玉峰等[12]研究了接触单元刚度取值、间隙宽度、桥台刚度以及支座滑动性能等非线性边界条件对碰撞效应的影响。试验研究方面，Guo等[13]针对两跨简支梁，进行了缩尺比1/20的振动台模型试验，试验研究了MR阻尼器及SMA装置减小碰撞效应的效果；李忠献等[14]采用一两跨缩尺隔震梁桥模型对其地震碰撞反应进行了振动台试验研究，试验表明：磁流变阻尼器安装在邻跨之间可以减小邻跨相对位移，且对墩顶位移不会产生明显影响；Wieser等[15]在内华达大学进行了2/5比例模型的试验测试，研究了桥台冲击对曲桥整体抗震性能的影响；Li等[16]也通过振动台试验研究了考虑行波效应和局部场地效应时典型曲桥的地震响应特性。

总结国内外研究现状，现阶段桥梁碰撞效应和碰撞影响研究主要存在以下不足：桥梁碰撞效应参数影响分析仍不全面，特别是未结合梁-台、梁-梁实际工作状态(桥梁纵坡、伸缩缝间隙及由于堵塞或者老化引起的间隙变化等)选择碰撞影响参数；地震动特性对碰撞效应影响分析不足，地震动时空特性(场地条件、速度脉冲、行波效应等)等对桥梁碰撞效应的影响分析仍不能满足设计需求；且现阶段的研究成果主要以数值分析结果为主，试验研究成果较少，相关研究结论缺少试验验证。为此，本文以某小半径带坡曲桥为对象，设计并制作了其1/10缩尺模型，设计了可调式碰撞测试装置，开展了试验模型桥的系列振动台试验，重点探究了碰撞对有纵坡曲线梁桥主梁、桥墩的动力响应影响。

1 振动台试验模型简介

1.1 模型概况

原型桥为一座3×40 m的曲线连续梁桥，曲率半径为50 m，纵坡3%(常见设计纵坡)，桥宽12 m。上部结构为变截面单箱双室预应力钢筋混凝土箱梁，梁高2.2 m；下部结构采用双圆柱墩。结合试验室空间和振动台参数，本文确定的试验模型几何缩尺比例为1/10，模型桥的主要相似关系见表1。依据相似关系，试验模型桥的主要设计参数及桥型布置图如图1所示。为便于说明与分析，定义沿1#墩与4#墩连线方向为X向，垂直于1#墩与4#墩连线方向为Y向。

表1 模型相似关系

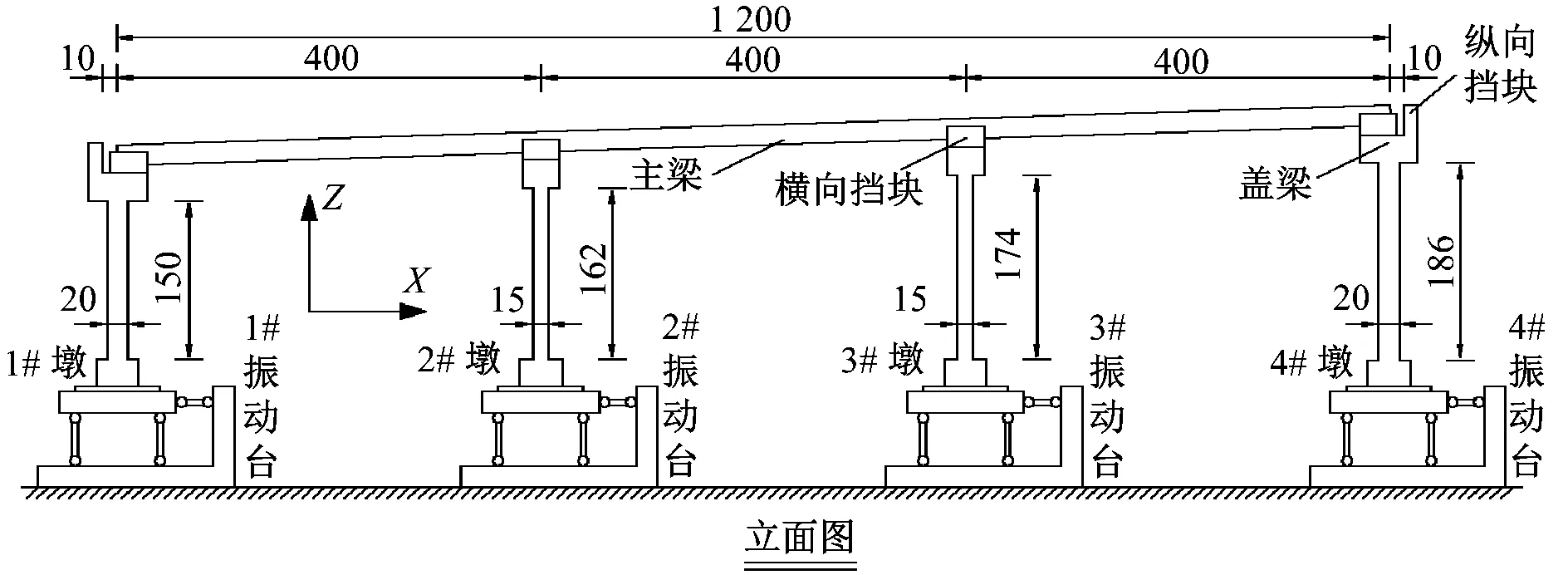
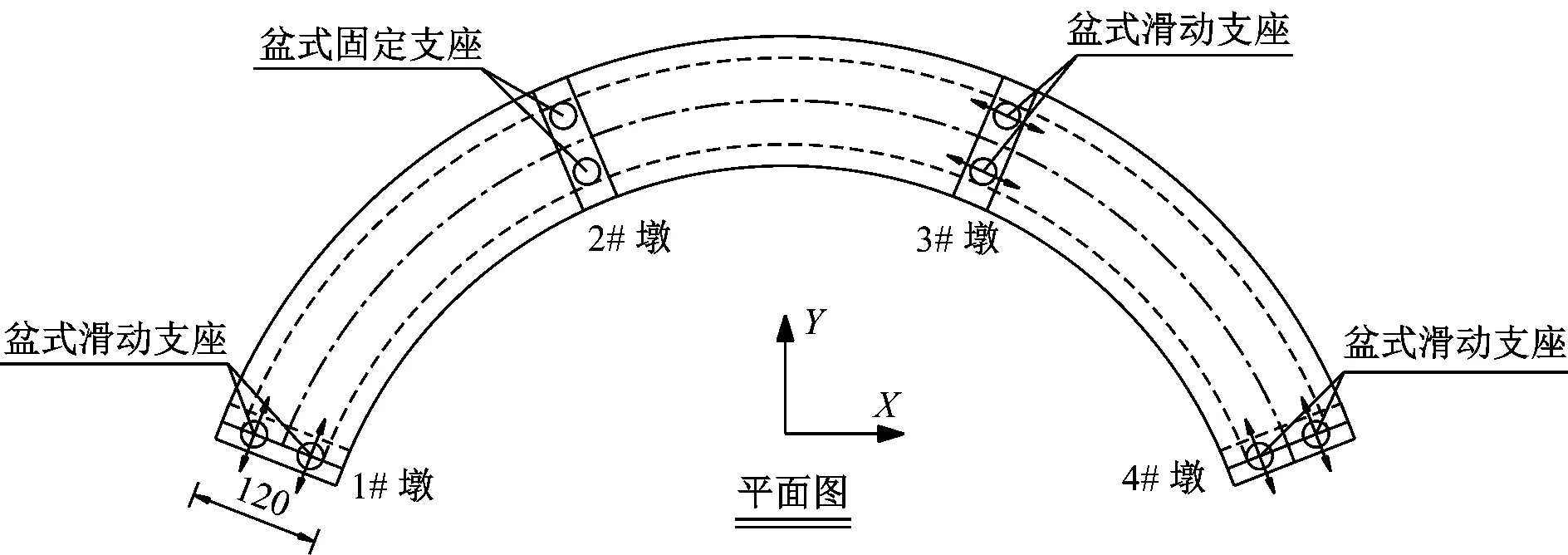
图1 试验模型布置图(cm)

1.2 振动台以及传感器布置

试验在北京工业大学工程抗震与结构诊治实验室进行，利用4个独立振动台组成的台阵系统完成，该系统按照曲线模型桥的线形进行布置，试验模型桥振动台布置如图2所示。试验中对模型桥关键点的加速度响应、位移响应和碰撞力进行量测，需要指出的是主梁纵坡为3%，其梁端垂直方向与铅直方向夹角仅为1.7°，主梁竖向加速度传感器通过AB胶粘贴于主梁表面，忽略传感器轴线(两端截面垂线)与铅直方向夹角的影响。为了考虑碰撞对模型桥地震响应的影响，作者利用NS-WL2型拉压力传感器(量程：10 t)、预留钢板、预留螺栓设计制作了可调式碰撞测试系统，通过预留螺栓的旋进与旋出实现不同的碰撞间隙参数。碰撞力测试装置如图3所示。模型桥测试装置布置如图4所示。

2 地震波激励与工况设置

依据《公路桥梁抗震设计细则》(JTG/T B02-01—2008)，原桥属于B类桥梁，桥址场地类别为Ⅱ类，场地特征周期Tg为0.45 s。不失一般性，针对原型桥所在地的地址条件分别选取三条实际地震动记录(Chi-Chi波、EL-Centro波、Taft波)，并依据规范反应谱理论设计了一条人工地震动作为振动台输入。为了避免桥梁发生损伤，试验中仅分析模型桥在设防烈度8度E1地震作用下的响应。振动台试验时，根据加速度幅值相似比将水平加速度峰值调整到0.5g，并按照频率相似比对地震波进行压缩。

图2 振动台试验模型照片

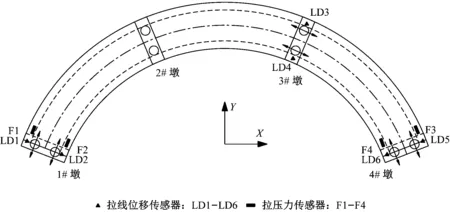
图4 传感器布置图

试验时分别沿X向、Y向和XY双向输入选取的地震动，具体试验工况见表2。为评价模型的工作状况，在每组试验工况开始前和完成后，沿XY向输入白噪声激励，以明确模型桥的基本动力特性参数变化。

表2 试验工况表

3 模型桥有效性评价

通过白噪声激励，作者利用FDD法(Frequency Domain Decomposition)对模型桥的基本动力特性进行了识别。图5给出了模型桥典型位置切向(沿模型桥轴线方向)、径向(沿模型桥曲率半径方向)加速度传感器的功率谱矩阵的奇异值。

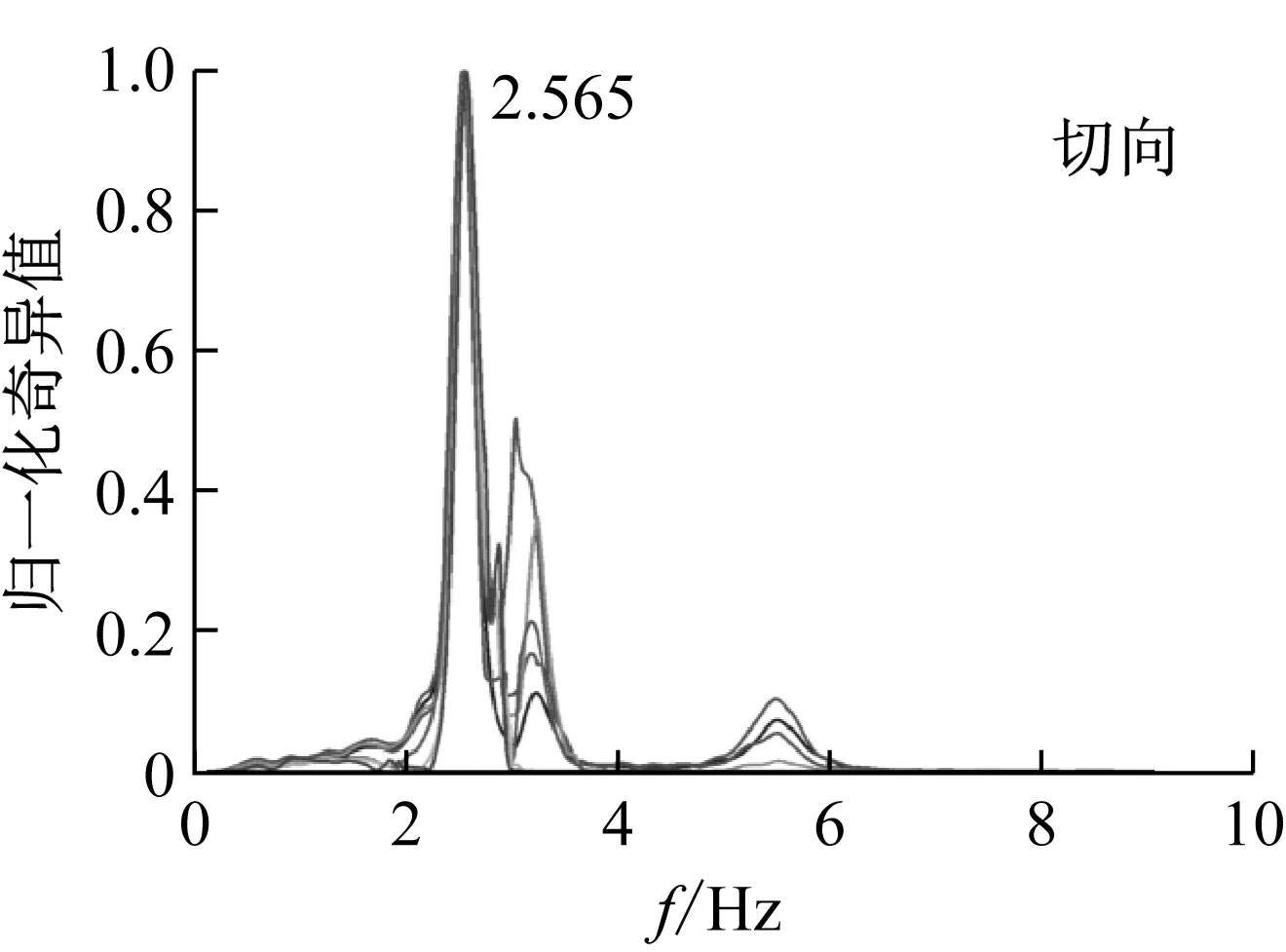
图5 模型测试功率谱密度奇异值

由图5可知，白噪声激励下，模型桥出现了三阶振动频率，模型桥前三阶自振频率分别为2.565 Hz、3.290 Hz和5.701 Hz。分析模型桥各墩墩顶加速度响应的自功率谱和互功率谱，并进行归一化以获取模型桥的基本振型，图6给出了模型桥的前三阶振型。

由图6可知，模型桥一阶振型为切向纵漂，二阶振型为径向对称弯曲，三阶振型为径向反对称弯曲。模型桥的前三阶振型频率均较低，在地震荷载下均易被激发。作为对比，表3给出了试验模型桥自振频率的有限元模型计算与实测结果。由表3可知，模型桥自振频率的理论计算值与实测值基本一致，模型桥设计有效。

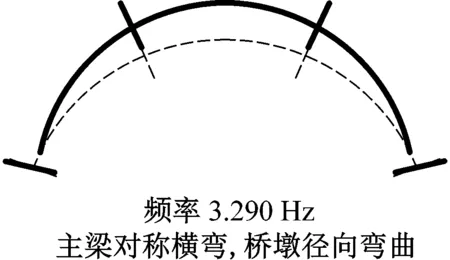
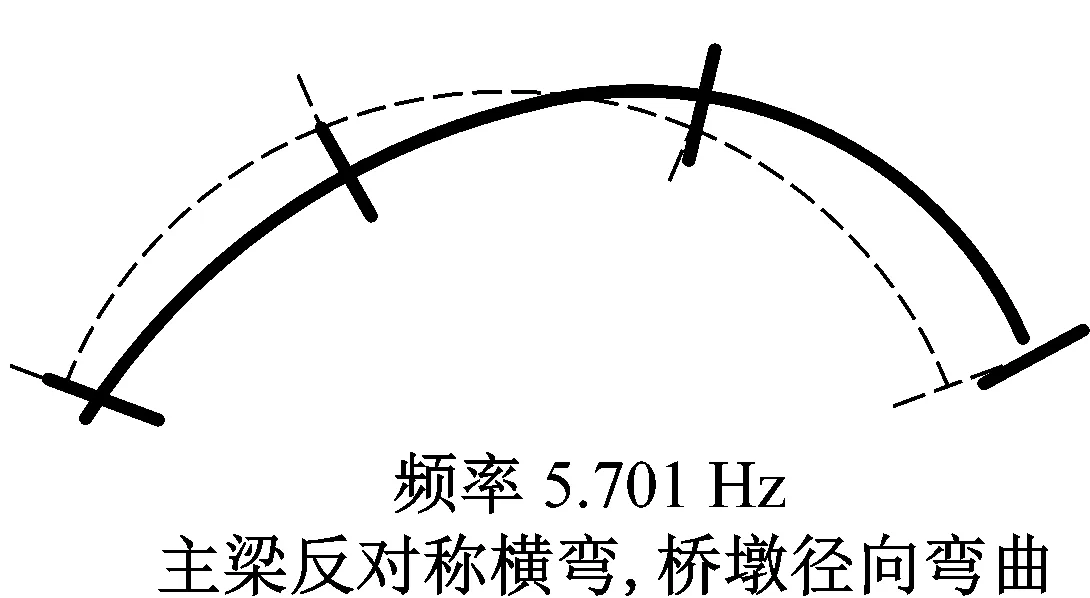
图6 模态识别信息

Fig.6 Modals of bridge model

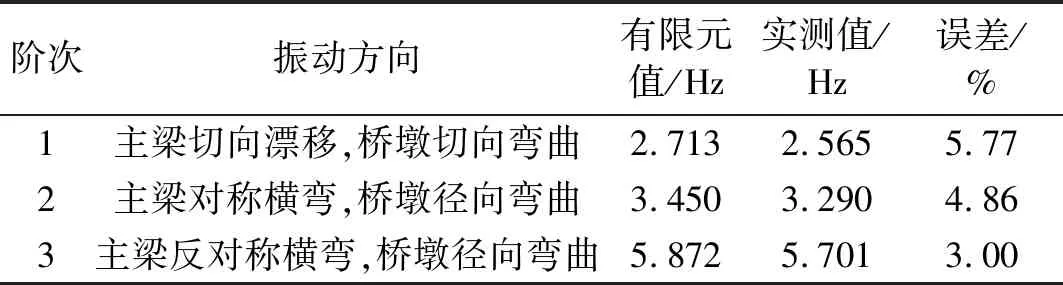
表3 有限元计算模态频率与实测值对比

4 试验结果分析

为了明确碰撞对曲线梁桥动力响应的影响，定义碰撞影响系数R来描述碰撞效应对曲线梁桥结构的动力响应的影响，如式(1)

R=100(Rp-Rnp)/Rnp

(1)

式中：Rp为考虑碰撞效应时曲线梁桥的动力响应值，可为主梁旋转角、主梁梁端加速度、墩顶相对位移等参数；Rnp为不考虑碰撞效应时曲线梁桥的动力响应值。R为正值表示碰撞效应导致桥梁结构动力响应增大，反之则表示碰撞效应导致桥梁结构动力响应减小。

4.1 主梁动力响应

4.1.1 面内旋转响应

依据模型桥的振型分析结果，地震荷载作用下，试验模型桥的动力响应主要包含沿轴线方向的水平平动、沿径向的水平平动以及绕模型桥几何中心平面内转动。由于曲率的影响，曲线桥在地震波的作用下，其主梁在平面内会表现出旋转的趋势，可以用旋转角φ来描述旋转的大小。

(2)

式中:uNi、uNj代表N号桥墩上内外侧支座的切向位移；l为内外侧支座中心点之间的距离，本试验中值为530 mm。

依据式(1)和(2)，图7给出了不同激励方向条件下，试验地震波作用下模型桥非固定墩处主梁面内旋转角碰撞响应影响系数均值。

由图7可知，不同激励方向条件下碰撞均使得主梁的旋转效应增大，且碰撞对模型桥高墩处旋转角影响程度远大于低墩。高墩处主梁旋转碰撞影响系数最大值为230%(双向激励时)；低墩处主梁旋转碰撞影响系数最小仅为2%(X向激励时)；3#墩处因距离高墩较近，受高墩碰撞反应的影响，其旋转响应也出现了增大现象，其主梁旋转碰撞反应影响系数最大值为115%(X向激励时)。为分析地震波沿Y向激励时试验模型桥的旋转效应与X向激励和双向激励时试验模型桥旋转效应的显著差异，图8给出了典型试验地震波作用下梁端的碰撞力时程曲线。

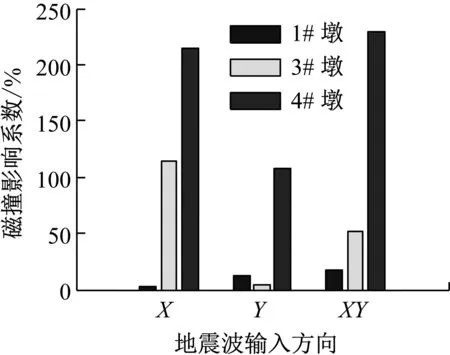
图7 主梁旋转角碰撞响应影响系数

由图8可知，X向和双向激励时试验模型桥的高、低墩处的碰撞时刻不同即碰撞交替发生，而Y向激励时高、低墩碰撞时刻一致(试验用地震波激励下均有此现象)，当主梁两端同时发生碰撞时，碰撞力引起的附加旋转力矩可部分抵消，导致试验模型桥在Y向激励时因碰撞引起的旋转效应降低。

4.1.2 加速度响应

由于纵坡的影响，碰撞力对主梁质心会提供附加弯矩，附加弯矩可能会引起主梁的竖向动力响应，本文对主梁的竖向和水平加速度响应均进行了测试。同时由于纵坡的影响，模型桥的高墩(4#墩)、低墩(1#墩)处的碰撞响应差异显著，鉴于试验用地震波激励下碰撞对主梁加速度响应的影响规律类似，X向激励与XY向激励均为高、低墩碰撞时刻不一致的工况，且与X向激励相比，XY向激励下碰撞力更大。限于篇幅，本节以EL Centro波为例，仅对高、低墩同时发生碰撞(Y向激励)及低墩单独发生碰撞(XY双向激励)时模型桥的主梁的加速度响应进行分析。

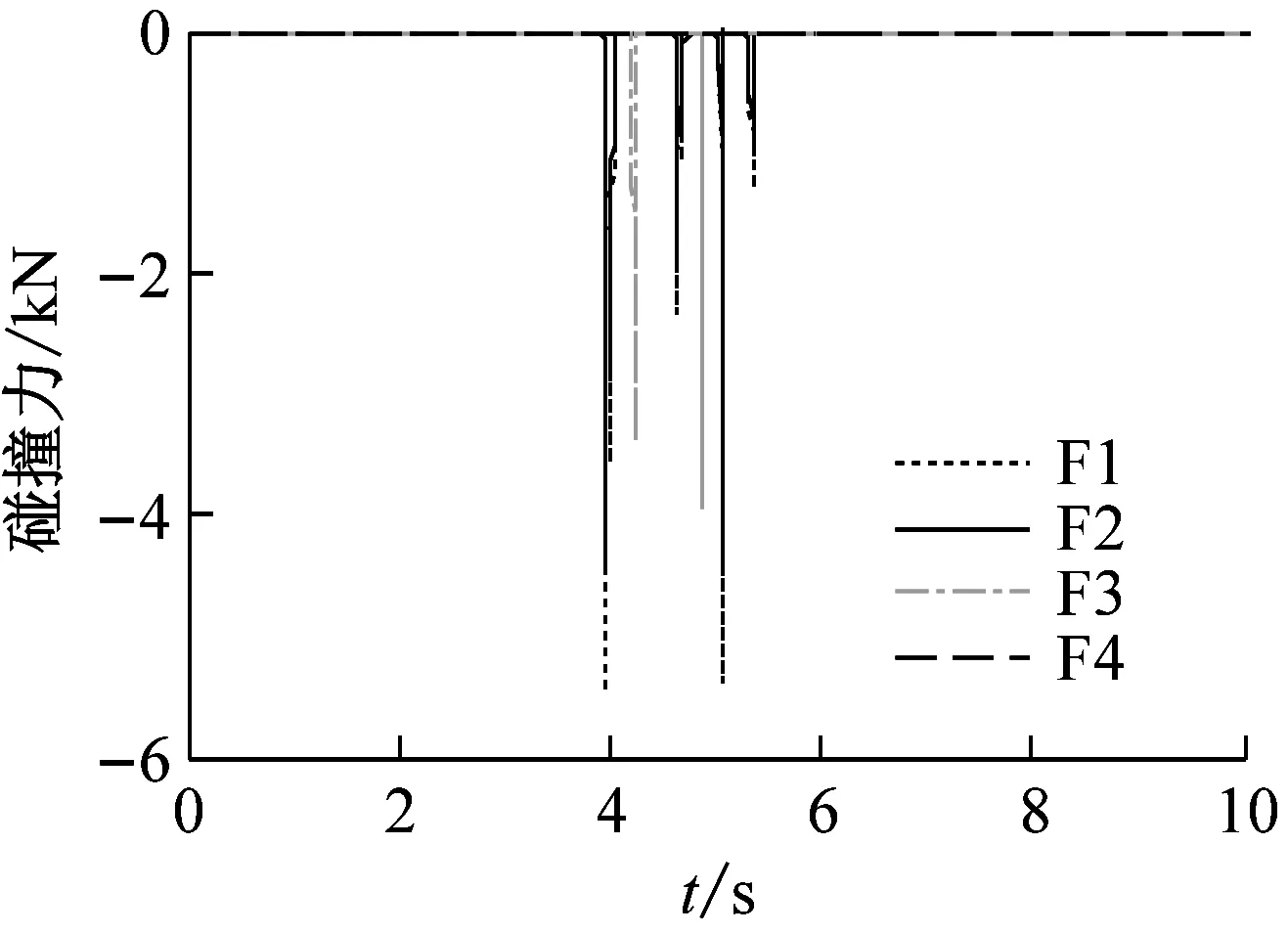
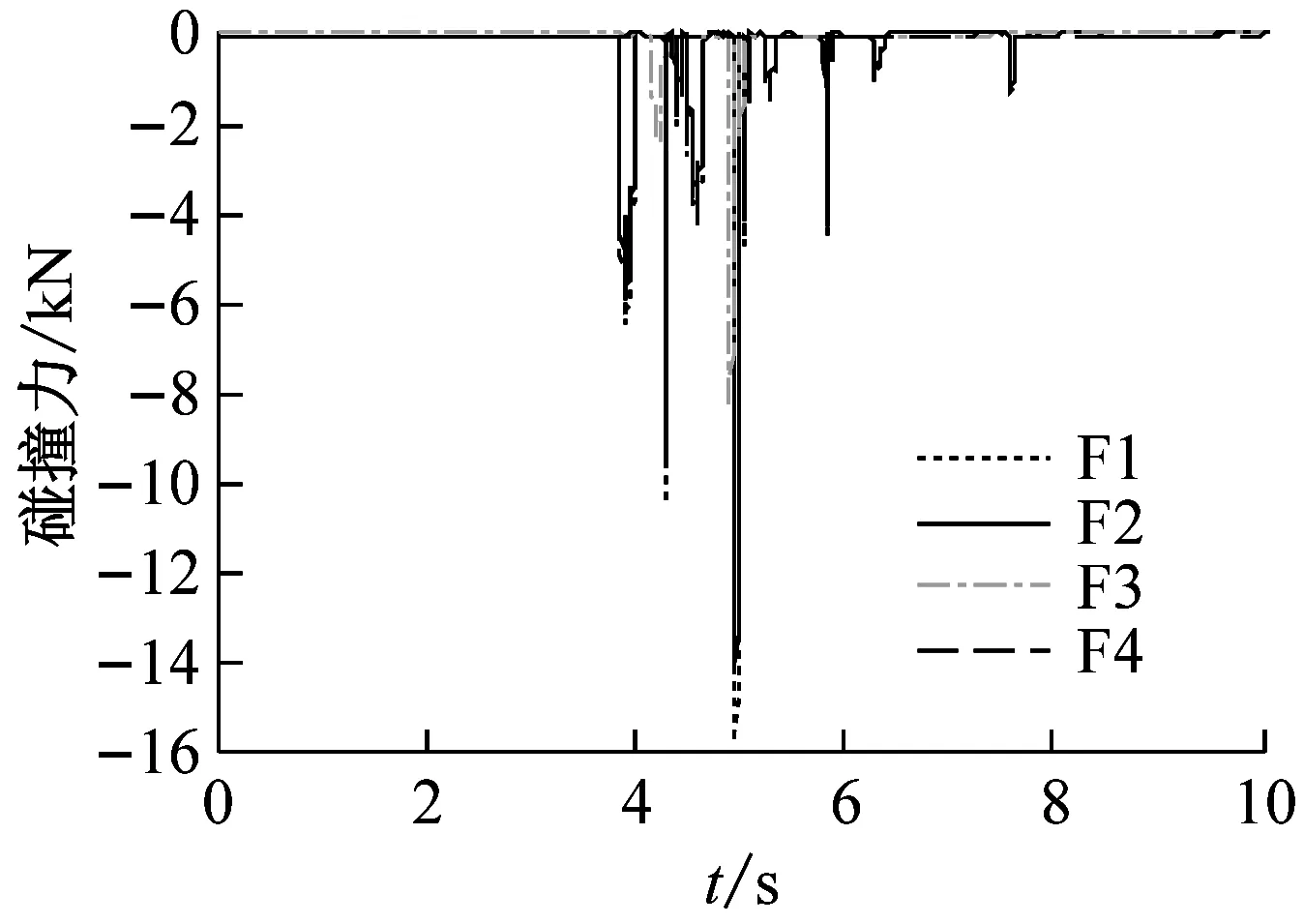
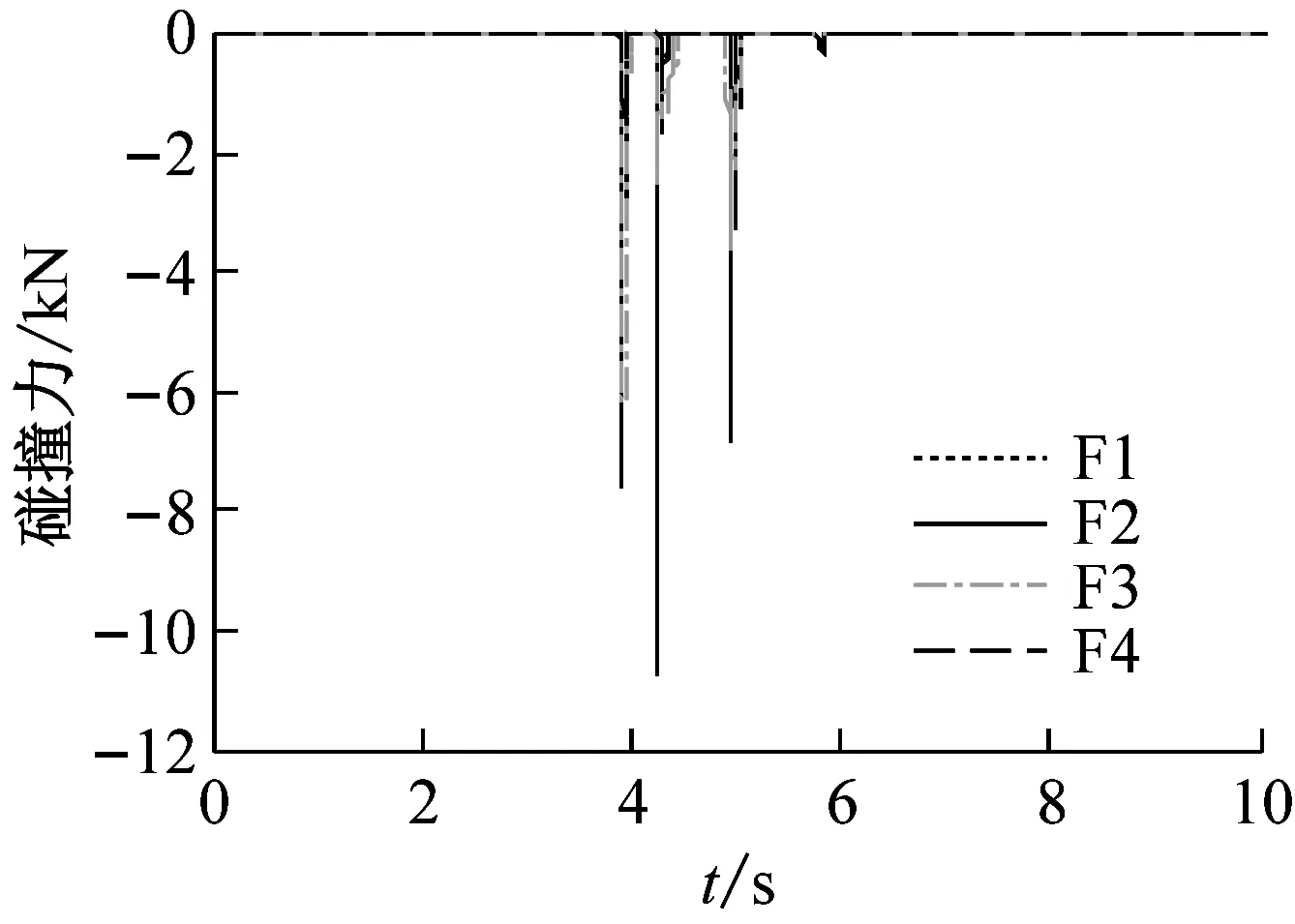
图8 Chi-chi波不同激励方向下的碰撞力响应时程

Fig.8 Time history of pounding in different excitation directions of Chi-chi waves

图9分别给出了Y向激励(高、低墩均发生碰撞)工况下碰撞效应对梁端切向和竖向加速度的影响时程曲线。

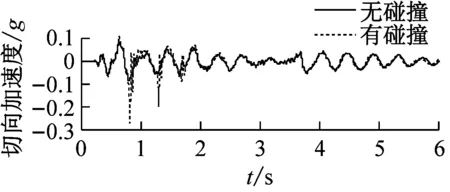
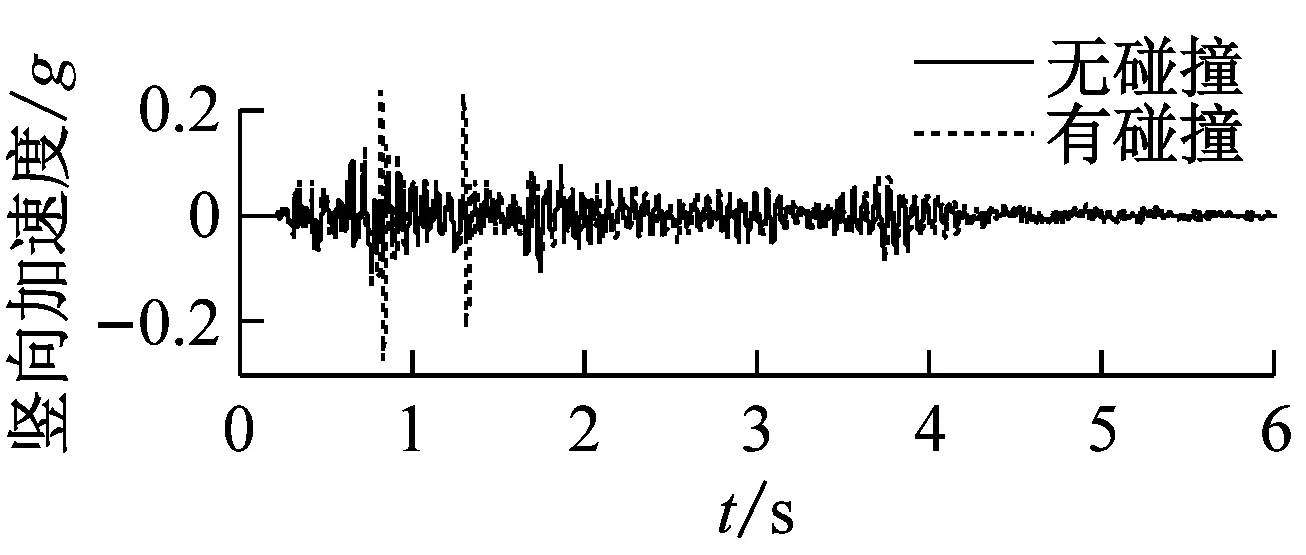
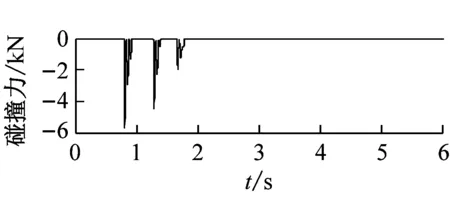
(a) 低墩处梁端地震响应

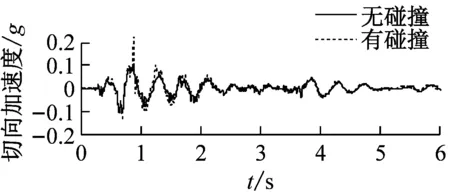
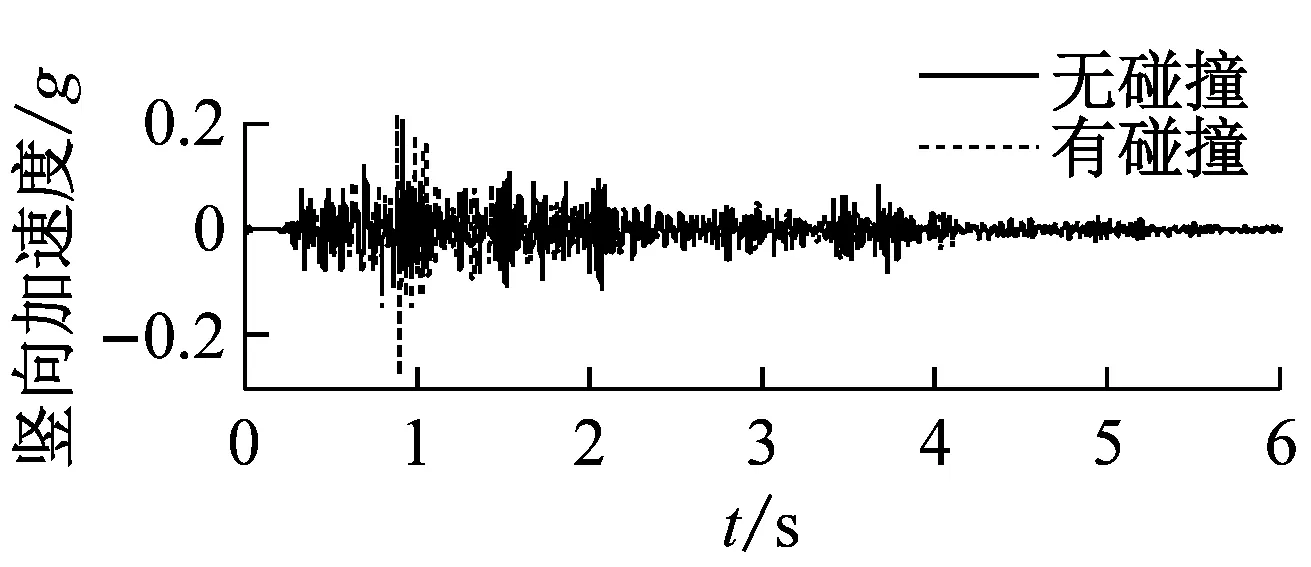
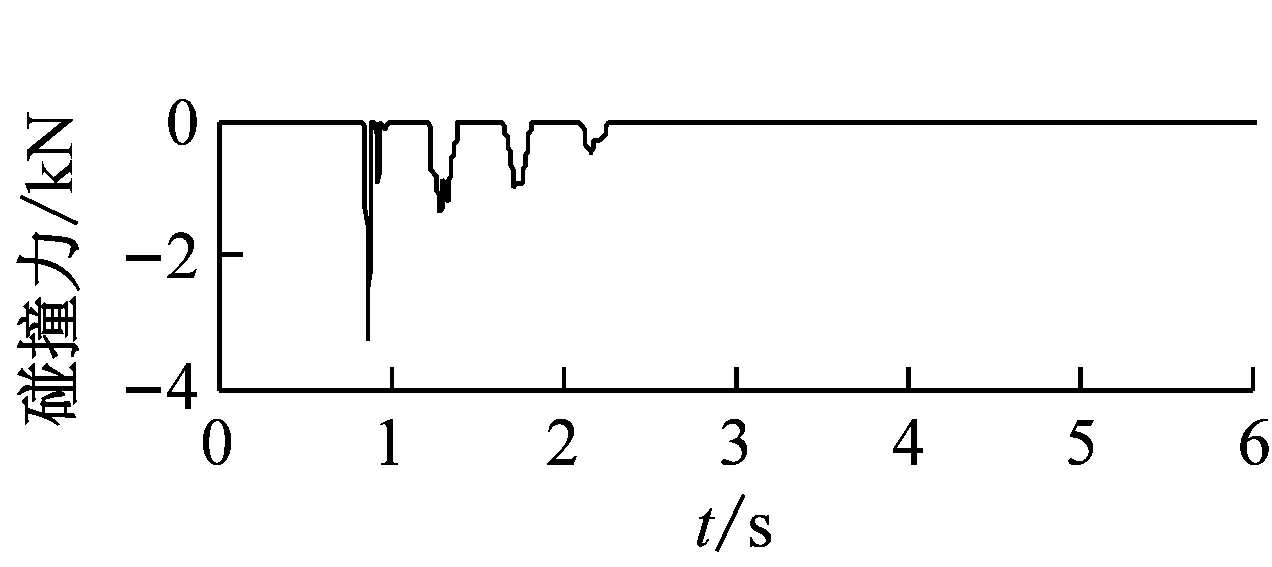
(b) 高墩处梁端地震响应

图9 EL-Centro波Y向激励梁端加速度时程曲线碰撞效应对比图

Fig.9 Time-history of the beam acceleration inYexcitation directions of EL-Centro waves

由图9可知，Y向激励，模型桥高、低墩处同时发生碰撞，存在0.82 s、1.3 s和1.7 s三个主要碰撞时刻，碰撞后高、低墩处主梁的切向加速度均有增大现象。低墩处的碰撞力相对较大，主梁的切向加速度碰撞影响系数在0.82 s最大，达到203%；高墩处主梁在同一时刻切向加速度也达到极值，切向加速度碰撞影响系数为104%。碰撞使高、低墩处主梁均产生了较大的加速度脉冲，其中低墩处主梁有两处明显的加速度脉冲，高墩处主梁有一处明显的加速度脉冲。

由于纵坡的影响，模型桥的高、低墩处主梁的竖向加速度碰撞影响系数最大值分别为121%和145%。碰撞作用下模型桥主梁的竖向加速度脉冲效应对其抗震性能有显著影响：一方面会在支座处产生一定的上拔力，可能会导致支座失效；另一方面可能会引起主梁竖向振动响应，增加主梁破坏风险；此外，竖向振动响应引起模型桥桥墩轴压比的变化，进而导致曲线梁桥桥墩在地震作用下的破坏模式的变化。因此，在进行地震响应分析时，应考虑碰撞后有纵坡梁桥主梁竖向动力响应对其地震响应规律的影响。

图10给出了EL-Centro波双向激励(低墩单侧发生碰撞)下碰撞效应对梁端切向和竖向加速度的影响时程曲线。

由图10可知，EL-Centro波双向激励下，低墩处较大的碰撞力使模型桥主梁出现了一定程度的水平、竖向加速度脉冲响应。低墩处主梁的切向和竖向加速度碰撞影响系数峰值达到了302%和123%；而在高墩侧，由于碰撞力很小(<1 kN)，模型桥主梁的在高墩侧的加速度碰撞影响系数变化不显著。

综上，碰撞后带纵坡的曲线梁桥主梁会出现较为显著的水平和竖向加速度脉冲响应，曲线桥主梁动力响应增加显著(特别是竖向动力响应)，碰撞会显著增加有纵坡曲线桥主梁在地震中发生破坏的风险。同时对比图9和图10，由于纵坡的影响，模型桥低墩处的撞击力要显著大于高墩处，试验工况下，低墩处的最大碰撞力约12.5 kN，而高墩处的最大碰撞力仅为3.5 kN。

4.2 桥墩动力响应

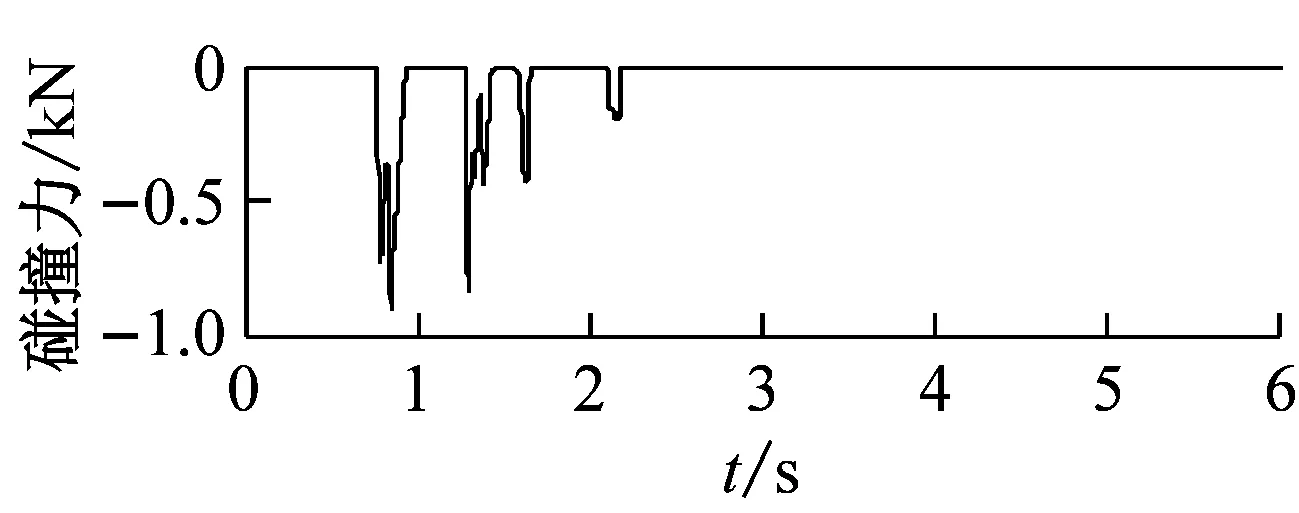
限于篇幅，以Chi-Chi波为例，图11给出了XY向激励下碰撞效应对1#墩(低墩)和4#墩(高墩)墩顶位移影响的时程曲线。

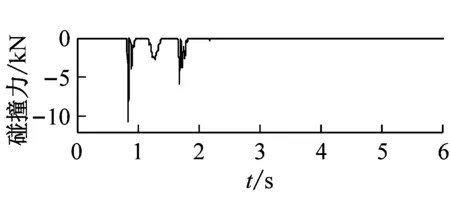
(a) 低墩处梁端地震响应

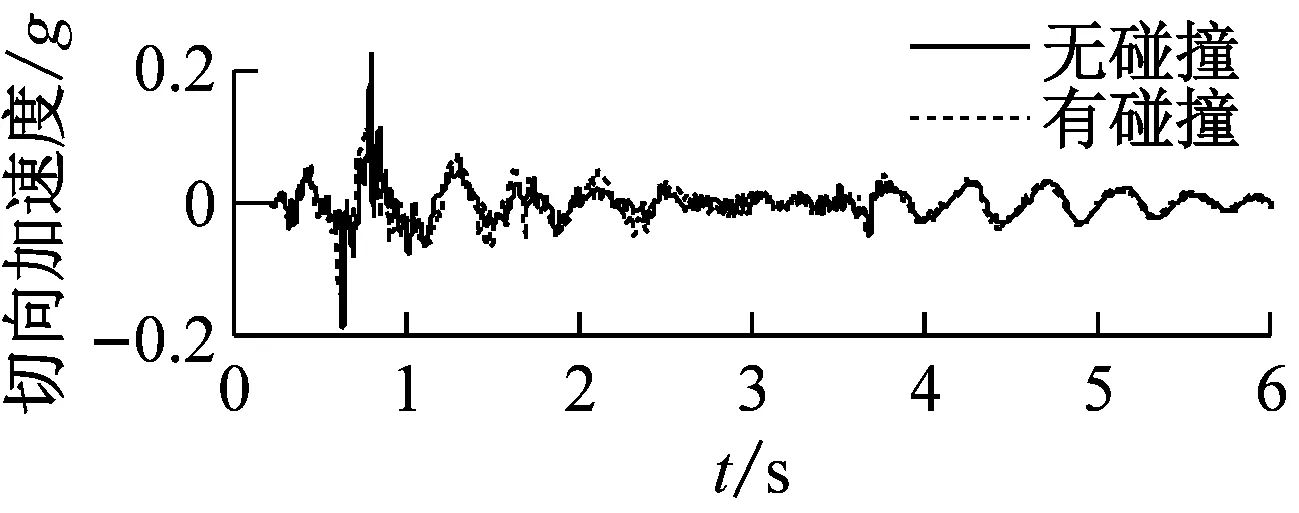
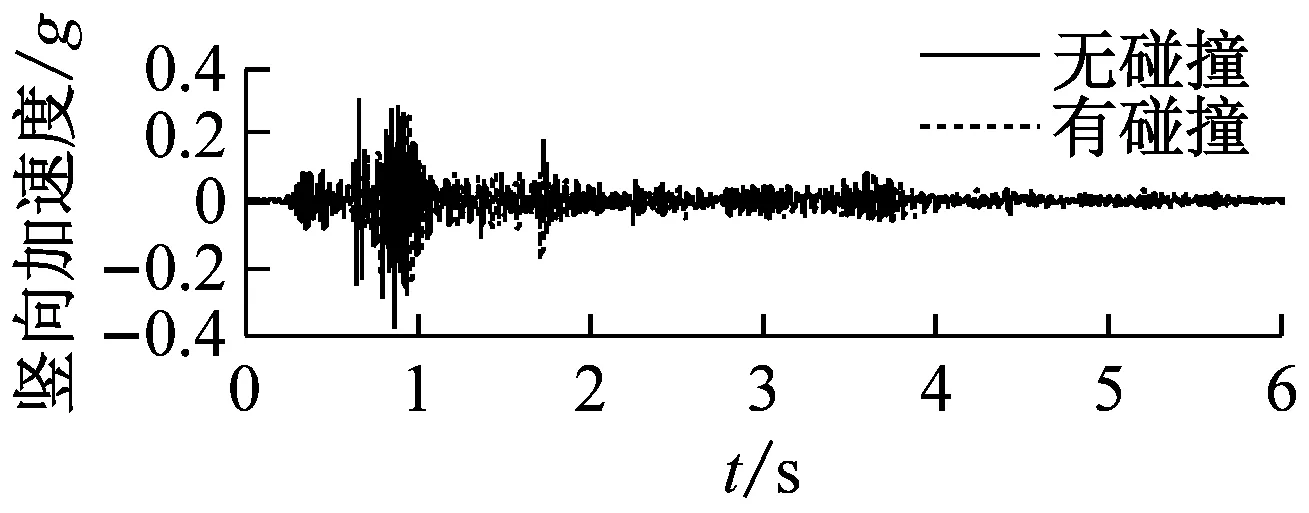
(b) 高墩处梁端地震响应

图10 EL-Centro波XY向激励高墩处梁端加速度时程曲线碰撞效应对比图

Fig.10 Time-history of the beam acceleration inXYexcitation directions of EL-Centro waves

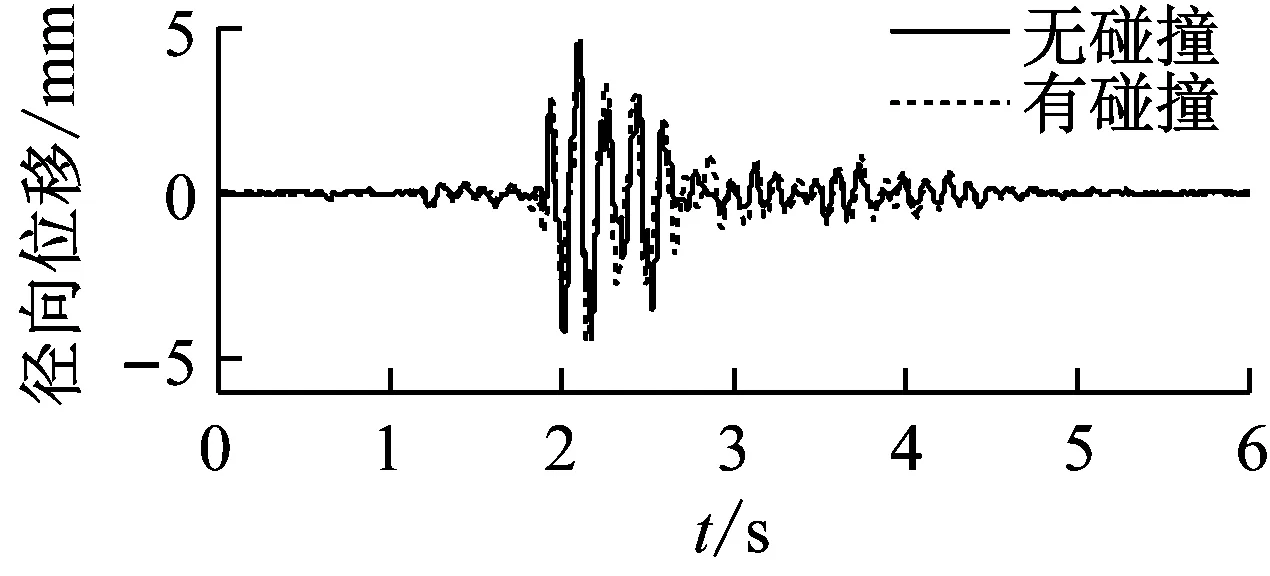
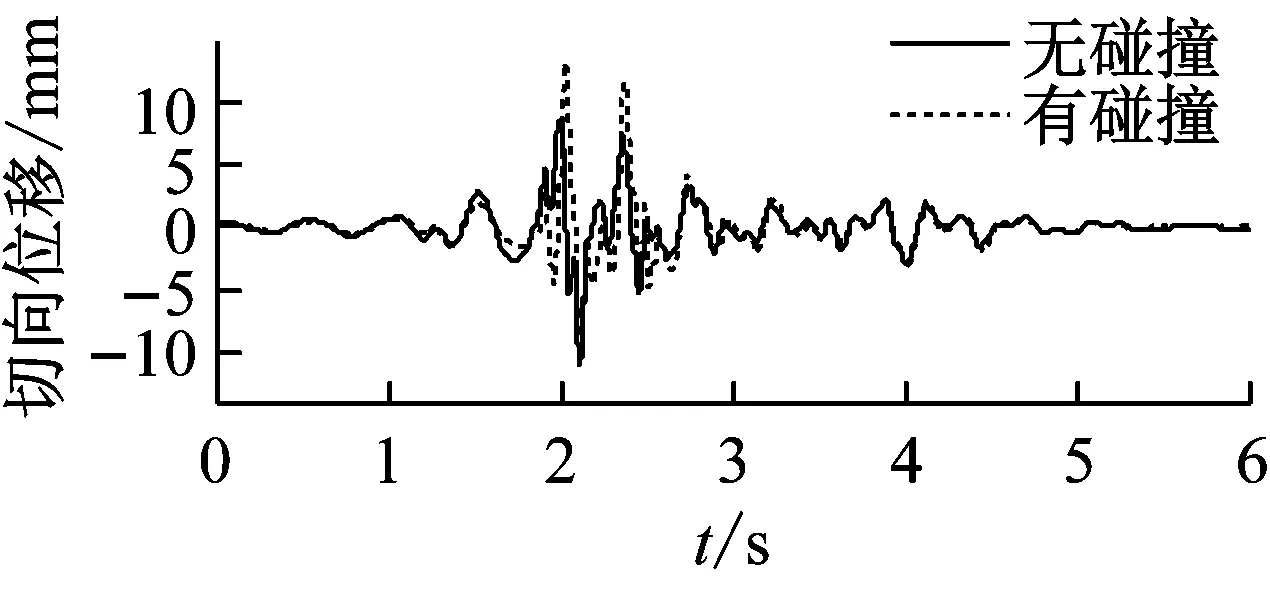
(a) 低墩位移时程曲线

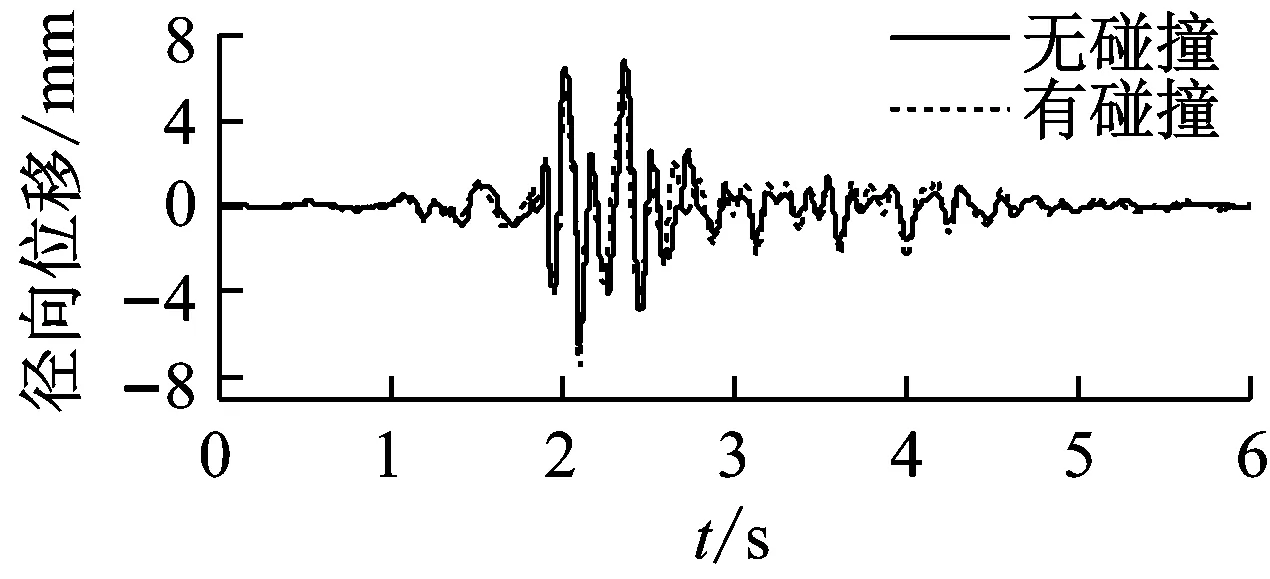
(b ) 高墩位移时程曲线

图11 Chi-Chi波XY向激励墩顶位移时程曲线碰撞效应对比图

Fig.11 Time history curve of pier displacement inXYexcitation directions of Chi-Chi waves

由图11可知，Chi-Chi波XY向激励下，碰撞后低墩墩顶切向位移响应有一定程度的增大，径向位移变化不显著。说明碰撞对径向位移不敏感，但由于碰撞效应的影响，桥墩在碰撞力相反方向上的切向位移增大，位移幅值由11.16 mm增长为13.27 mm(影响系数为18.88%)。同样，对于高墩，碰撞后径向位移略有增加，而切向位移由于产生了同向追逐碰撞使得反向位移有了明显的增大，位移幅值由8.39 mm增长为10.50 mm(影响系数为25.16%)。

表4给出了四条波不同工况作用下模型桥墩顶位移碰撞影响系数统计。

由表4可知，碰撞效应对桥墩位移响应的影响受地震波影响显著，试验地震波作用下，模型桥墩顶位移碰撞影响系数在-37.22%～+68.57%，结合模型桥的墩顶位移响应试验结果，当试验用地震波的反应谱谱值越大，试验模型桥的墩顶位移响应越大，试验模型桥的碰撞力有增大趋势。但墩顶位移影响系数不仅与碰撞力有关，还受碰撞对象的运动方向和墩顶支座约束条件等多种因素的制约。总的来说，同一次地震作用下，模型桥的桥墩墩顶位移增加幅值显著大于减小幅值，碰撞会显著增加模型桥桥墩在地震中发生损坏的几率，在进行桥梁抗震设计时应考虑碰撞效应的影响。

5 结 论

本文设计并制作了某小半径曲线梁桥的1/10缩尺模型，设计了可调式碰撞测试装置，通过振动台试验分析了碰撞对有纵坡曲线梁桥主梁、桥墩的动力响应影响。结果表明：

(1) 碰撞效应对曲线桥高、低墩处面内旋转响应影响不同，碰撞效应对高墩处主梁的旋转响应影响较低墩处显著。碰撞后，模型桥主梁高墩处的旋转响应显著增大，其主梁旋转碰撞影响系数最大值达230%。

(2) 碰撞效应对有纵坡曲线桥的主梁加速度响应影响显著。碰撞引起了有纵坡曲线桥梁端的水平和竖向加速度脉冲响应，其显著增加了模型桥的主梁加速度响应，特别是主梁的竖向加速度响应，试验模型桥的主梁竖向加速度响应碰撞影响系数最大值达302%；同时由于纵坡的影响，模型桥低墩处的撞击力要显著大于高墩处，试验工况下，低墩处的最大碰撞力约12.5 kN，而高墩处的最大碰撞力仅为3.5 kN。

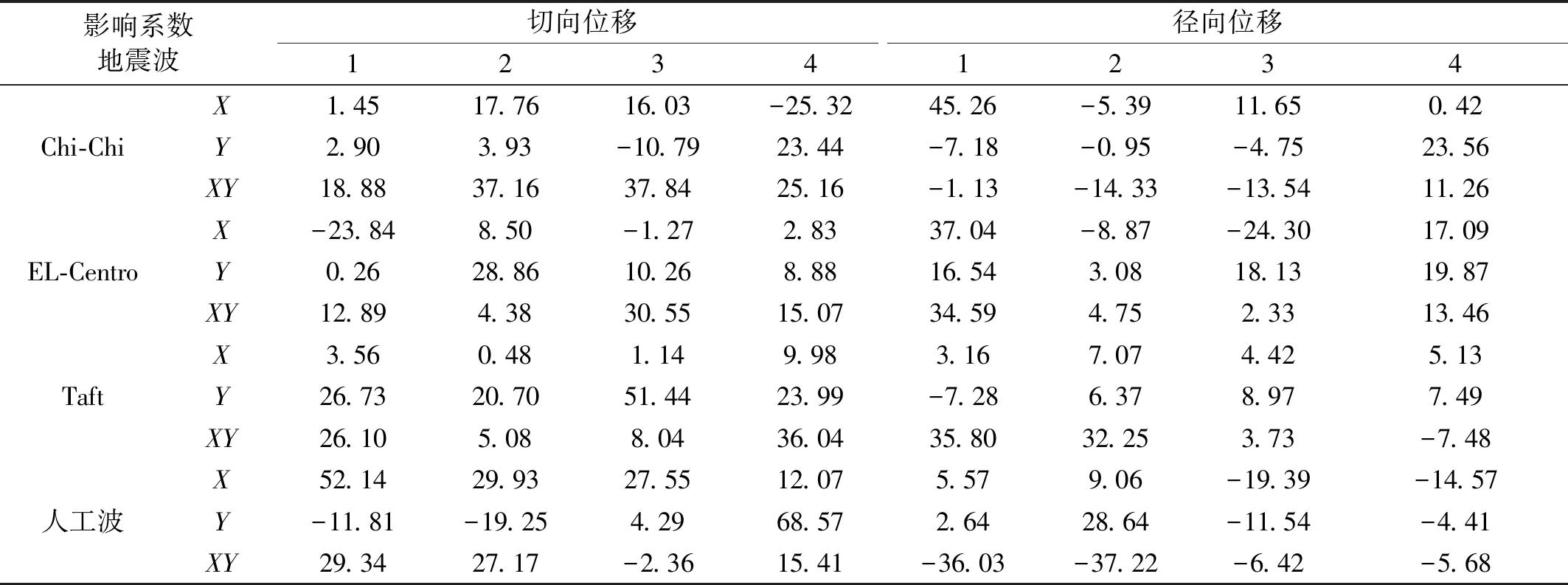
表4 墩顶位移碰撞效应影响系数表

(3) 曲线桥桥墩动力响应的碰撞效应影响系数在-37.22%～+68.57%。说明在同一次地震中，碰撞对曲线桥桥墩墩顶位移的放大作用显著大于其对桥墩墩顶位移的减小作用，碰撞会显著增加曲线桥桥墩在地震中的破坏可能，在进行桥梁抗震设计时应考虑碰撞的影响。

需要指出的是本文并未考虑非弹性碰撞及横向碰撞对带纵坡曲线梁桥地震响应的影响，同时未涉及地震动空间变化性和近断层地震动特性等对相关试验结果的影响，相关研究将是下一步工作的重点。