基于反馈变分模式分解的单通道盲源分离算法
赵知劲, 黄艳波, 强芳芳, 杨安锋
(1.杭州电子科技大学 通信工程学院,杭州 310018; 2. 杭州电子科技大学 电子信息学院,杭州 310018)
常规的多通道盲源分离( Blind Source Separation,BSS)算法不适用于单通道盲源分离(Single Channel BSS,SCBSS),目前对SCBSS的解决方法主要有三类:①基于循环谱域滤波的SCBSS算法[1-3];②基于信号参数差异的SCBSS算法[4-6];③基于虚拟多通道的SCBSS算法[7-13]。前两类算法性能与源信号特性密切相关,第三类算法常用小波分解、小波包分解、经验模态分解(Empirical Mode Decomposition, EMD)和增强经验模态分解(Essential EMD,EEMD)与ICA结合,但是小波基和分解层数选择困难、EMD分解经常出现模态混叠现象等问题,这些直接影响算法的分离性能。
Dragomiretskiy等[14-15]提出了基于变分模式分解(Variational Mode Decomposition, VMD )的单通道盲源分离(VMD-SCBSS)算法,但是该算法需要预先知道模态数K。高艳丰等[16]提出一种基于变分模式分解和 Teager 能量算子相结合的高压输电线路雷击故障行波检测方法。马增强等[17]针对滚动轴承早期故障振动信号信噪比低、故障特征提取困难的问题,提出了基于变分模式分解和能量算子的滚动轴承故障特征提取方法,并提出了一种确定模式数K的方法。针对混合的源信号数未知,本文提出基于反馈VMD的通信信号SCBSS算法。
1 VMDF-SCBSS算法
1.1 变分问题的构造
VMD是基于维纳滤波、Hilbert变换和混合频率的变分问题的求解过程,通过寻找约束变分模式最优解自适应地将信号分解成一系列的具有稀疏特性的模式分量。
VMD的目的是将待分析信号x(t)分解成K个具有特定稀疏性的模式信号uk(t),每个uk(t)的带宽之和最小,其约束条件是各个uk(t)之和等于待分析信号。
利用Hilbert变换计算每个uk(t)的解析信号为
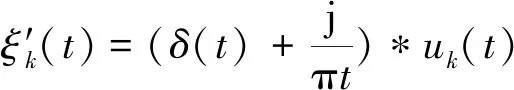
(1)
并将各个模式的频谱调制到相应的基频带,即
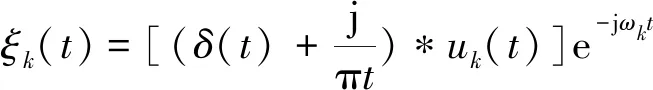
(2)
估计各个模式的带宽,约束变分问题可表示如下
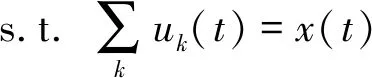
(3)
式中:uk(t)={u1(t),…,uK(t)};ωk(t)={ω1(t),…ωK(t)}。
为了求解式(3)变分问题,引入二次惩罚因子α和拉格朗日乘法算子λ(t),即将约束优化问题转换成非约束优化问题,如式(4)所示。其中α的取值保证信号重构精度,λ(t)使约束条件保持严格性。
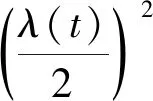
(4)

(5)
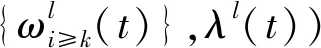
(6)
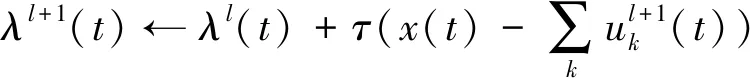
(7)
收敛条件如式(8)所示
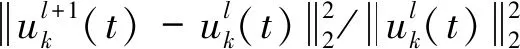
(8)
1.2 频域更新公式推导
由于uk(t)和ωk(t)的更新困难,本文从频域进行更新,然后傅里叶反变换实现uk(t)和ωk(t)的更新式。
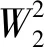
(9)
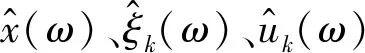
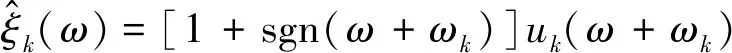
(10)

(11)
将式(11)第一项中的ω用ω-ωk替换并计算2-范数,可得:
(12)
令
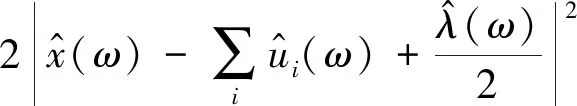
(13)
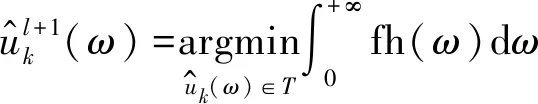
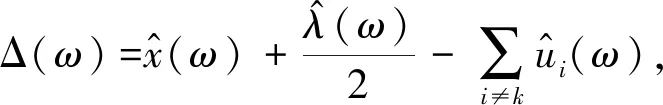
2Δ*(ω)=0
(14)
2Δ(ω)=0
(15)
由式(14)和式(15)求得最小值解为
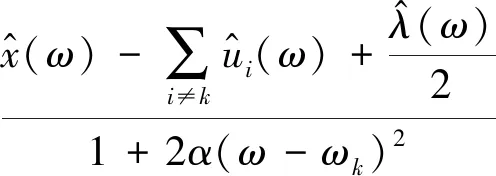
(16)
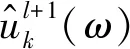
与uk(t)的最小化问题处理方式相同,将中心频率更新问题转换到频域。由式(13)可知,fh(ω)的第二项不包含ωk,因此可得
(17)
求最小值解可得
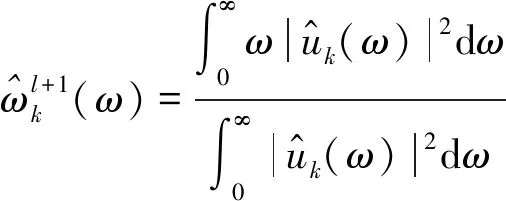
(18)
此中心频率是在模式中观察到的瞬时相位的最小二乘线性回归的频率。
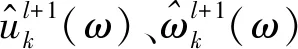
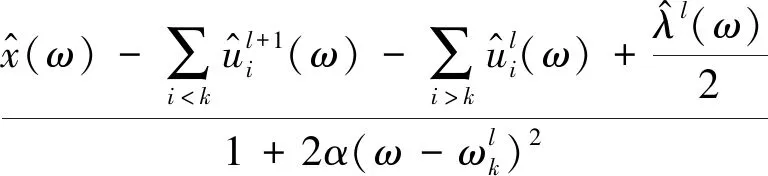
(19)

(20)
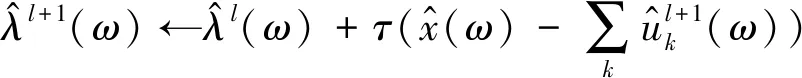
(21)
式中:τ为带宽。
1.3 VMDF-SCBSS算法
将VMD应用于单通道盲源分离(将此方法简记为VMD-SCBSS),VMD分解得到的模式分量uk(t)就是对应的源信号,但由式(19)、式(20)和式(21)可知,VMD算法需要预先确定模式数目K。VMD-SCBSS算法在源信号数目未知的情况下,K值需由VMD得到的频谱判断,其值与算法预先设定的中心频率差值Δf有关。如果设定的Δf较大,可能发生欠分解;如果设定的Δf较小,可能发生过分解。所以,Δf设置不合理,可能引起K判定失误,从而影响源信号分离。
针对此问题,本文提出了基于反馈VMD的SCBSS(简记为VMDF-SCBSS)算法,该算法无需预先设置Δf。反馈VMD就是将每次分解得到的最纯的模式分量反馈到VMD的输入端,并在VMD的输入端减去这个模式分量,将剩余的信号作为新的信号继续进行二模式的VMD,重复这个过程,直到混合信号分解完全。
令第Kn次分解得到的模式分量为uKn,1(t)和uKn,2(t)与观测信号x(t)的相似系数分别为δKn,1和δKn,2,δKn,i(i=1,2)的计算如式(22)所示
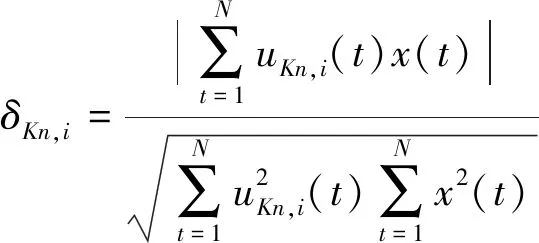
(22)
根据式(23)求I,则最纯模式分量为uKn,I(t)。
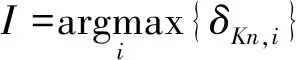
(23)
分解完全的判别条件为
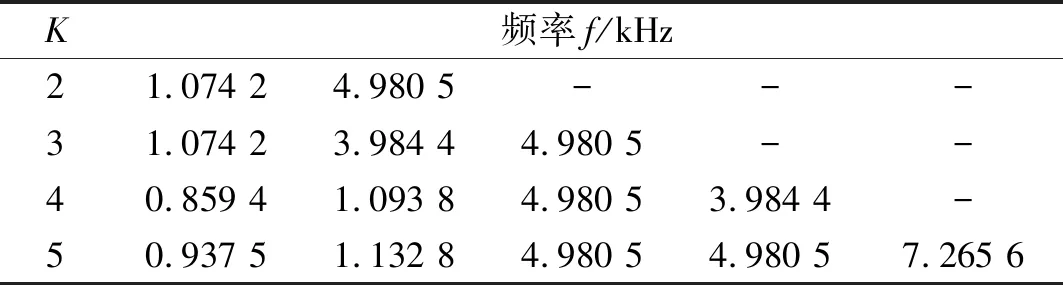
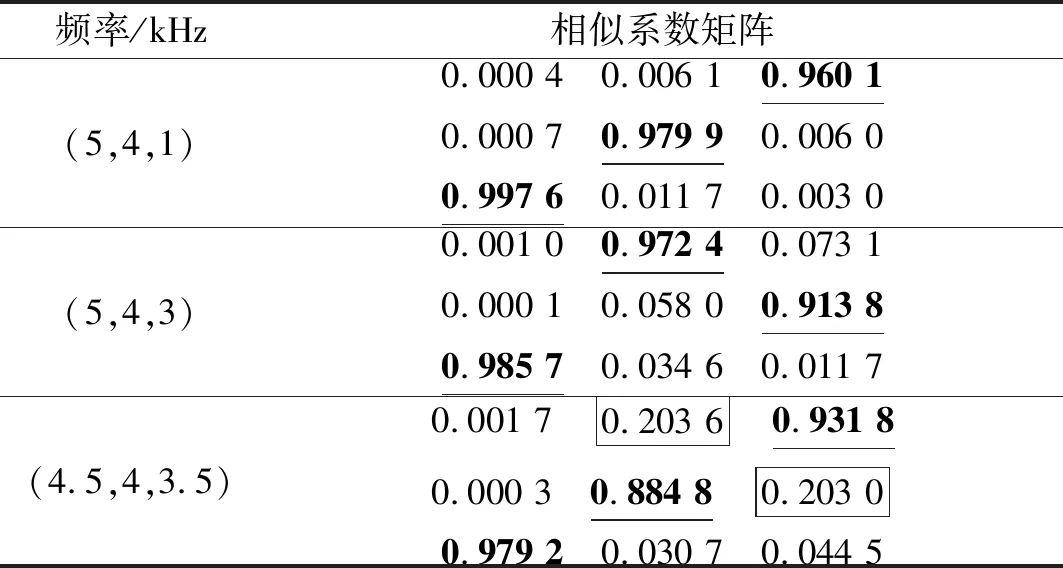
max{δKn,1,δKn,2} (24) 因此,本文提出的基于反馈VMD的SCBSS算法主要步骤如下: 步骤1 模式数目K=2,初始化迭代次数Kn=1,xKn(t)=x(t)。 步骤3 利用式(22)计算相似系数δKn,1和δKn,2,利用式(23)得到分解最纯模式分量uKn,I(t)(I取1或2)。 步骤4 当式(24)成立时,停止反馈和分解,源信号个数等于Kn+1。否则转“步骤5”。 步骤5 将步骤3选取的模式分量uKn,I(t)反馈到VMD的输入端,并从输入信号中减去该模式分量,即xKn+1(t)=xKn(t)-uKn,I(t)。xKn+1(t)作为新的VMD输入,令Kn=Kn+1,重复“步骤2”~“步骤4”过程。 根据上述算法不仅能够实现单通道的盲源分离,而且可以确定源信号数目为Kn+1。 本节仿真分析VMDF-SCBSS算法性能,并与VMD-SCBSS算法比较。仿真中余弦信号、2ASK和BPSK调制信号作为源信号s1(t)、s2(t)和s3(t),采样速率为20 kHz,幅度均为1;单通道观测信号为x(t)=A·S(t),其中A是一维随机行矢量;S=[s1(t)s2(t)s3(t)]T。算法中参数设置如下:ε=1×10-7,惩罚因子和带宽使用默认值,即α=2 000,τ=0。 s1(t)、s2(t)和s3(t)的载频分别为5 kHz、4 kHz和1 kHz,不同K值VMD-SCBSS算法得到的各模式中心频率如表1所示。 表1 不同K值时VMD-SCBSS算法得到的各模式中心频率 由表1可知,VMD-SCBSS算法的分离性能受K值影响大。当K未知时,VMD-SCBSS算法需依据频率间隔Δf确定模式数目K,不同的Δf对分离结果有较大的影响。根据文献[17]确定模式数目K方法和表1可知,Δf=1 kHz时,确定的模式数目为K=2,小于源信号数目3,设置的Δf过大;Δf=0.5 kHz时,确定的模式数目为K=3,设置的Δf正好合适;Δf=0.1 kHz时,确定的模式数目为K=4,大于源信号数目3,设置的Δf过小。由此可知,VMD-SCBSS算法性能受Δf影响大。 2.2.1 最纯模式分量确定 在无噪情况下,迭代次数Kn=1时,由VMDF-SCBSS算法分离得到的信号u1,1(t)和u1,2(t)与观测信号x(t)的相似系数δ1,1、δ1,2及u1,1(t)和u1,2(t)与源信号S(t)的相似系数矩阵δS1如表2所示。 表2 δ1,1、δ1,2和δS1 由表2可知,δ1,2δ1,1,根据本节提出的算法可知,u1,2(t)是最纯模式分量,可作为一路源信号反馈到VMD的输入端;δS1的第一列第二行的数值接近于1,即u1,2(t)与源信号s1(t)的相似系数为0.990 8,验证u1,2(t)是一路源信号。 将u1,2(t)反馈到输入端,并从信号x1(t)中减去,剩余信号记为x2(t)。此时Kn=2,VMDF-SCBSS算法得到的信号u2,1(t)和u2,2(t)与观测信号x(t)的相似系数δ2,1、δ2,2及u2,1(t)和u2,2(t)与源信号S(t)的相似系数矩阵δS2,如表3所示。 表3 δ2,1、δ2,2和δS2 由表3可知,δ2,1δ2,2;u2,1(t)是最纯模式分量,可作为源信号的一路信号。同样δS2的第三列的第一行的数值接近于1,即u2,1(t)与源信号s3(t)的相似系数为0.958 2,验证了u2,1(t)是源信号的估计。 2.2.2 迭代终止判断 由表2和表3可知,δ1,2δ1,1δ2,1δ2,2,也就是说Kn=2时,分离信号与观测信号的相似系数的最大值小于Kn=1时的分离信号与观测信号的相似系数最小值。根据本节提出的VMD停止条件可确定Kn=2时VMD已经完成,源信号个数为Kn+1=3个,且u1,2(t)、u2,1(t)、u2,2(t)分别是源信号s1(t)、s3(t)、s2(t)的估计。 为了证明Kn=2时分解已经成功,令Kn=3,由VMDF-SCBSS算法得到分离信号u3,1(t)和u3,2(t)与x(t)的相似系数δ3,1、δ3,2及u3,1(t)和u3,2(t)与源信号S(t)的相似系数矩阵δS3,如表4所示。 表4 δ3,1、δ3,2和δS3 比较表3和表4可知,这次分解得到的u3,2(t)是源信号s2(t)的估计,与u2,2(t)相同,所以这次分解没有意义,即Kn=2时已经将源信号全部分离。 2.2.3 源信号载频对分离性能的影响 当余弦信号、2ASK和BPSK信号的载频(fc1,fc2,fc3)分别为(5,4,1) kHz、(5,4,3) kHz和(4.5,4,3.5) kHz时,VMDF-SCBSS算法得到分离信号与源信号s1(t)、s2(t)和s3(t)的相似系数矩阵,如表5所示。 表5 VMDF-SCBSS算法相似系数矩阵 表5中:加粗加下划线的数字表示该元素理想情况应为1;带框的数字表示理想情况为零,现该元素值大于0.2。由此可见,源信号载频相差越大,VMDF-SCBSS算法分离性能越好。 2.2.4 实际信号分离性能 载频分别为5 kHz和1 kHz的余弦信号和2ASK信号混合后,由基于AD9361的软件无线电平台发射并采集,源信号和由VMDF-SCBSS算法分离的分离信号的部分波形如图1所示。 (a) 源信号_余弦信号 (b) 源信号_2ASK信号 (c) 分离信号_余弦信号 (d) 分离信号_2ASK信号 图1 VMDF-SCBSS算法分离效果 Fig.1 VMDF-SCBSS algorithm separation performance 2.3.1 分离性能比较 信号参数同“2.1”节,K=3。不同信噪比条件下,VMDF-SCBSS算法和VMD-SCBSS算法得到的分离信号与源信号的平均相似系数,如图2所示。 图2 不同信噪比条件下两种算法的平均相似系数 由图2可知,VMDF-SCBSS算法分离性能优于K值已知的VMD-SCBSS算法性能;低信噪比时用VMD-SCBSS算法分离性能较差,大于8 dB时平均相似系数大于0.9,分离效果较好,而VMDF-SCBSS算法在信噪比大于5 dB时,就能达到较好的分离效果。 2.3.2 复杂度分析 将反馈机制引入VMD中,提出了基于反馈VMD的单通道盲源分离(VMDF-SCBSS)算法,该算法分离性能优于VMD-SCBSS算法,不需要预先设置频率间隔Δf参数,能够自动确定源信号数,算法复杂度低于后者。如何进一步提高源信号载频靠得较近时分离性能值得进一步研究。2 算法仿真与性能分析
2.1 K对VMD-SCBSS算法的影响
2.2 VMDF-SCBSS算法



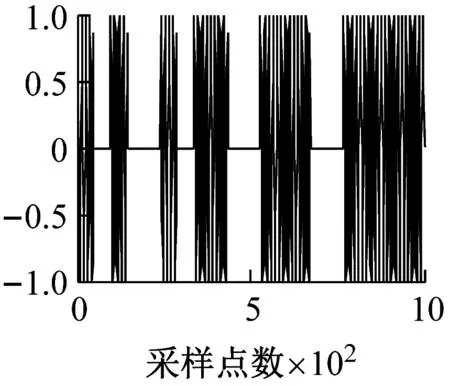
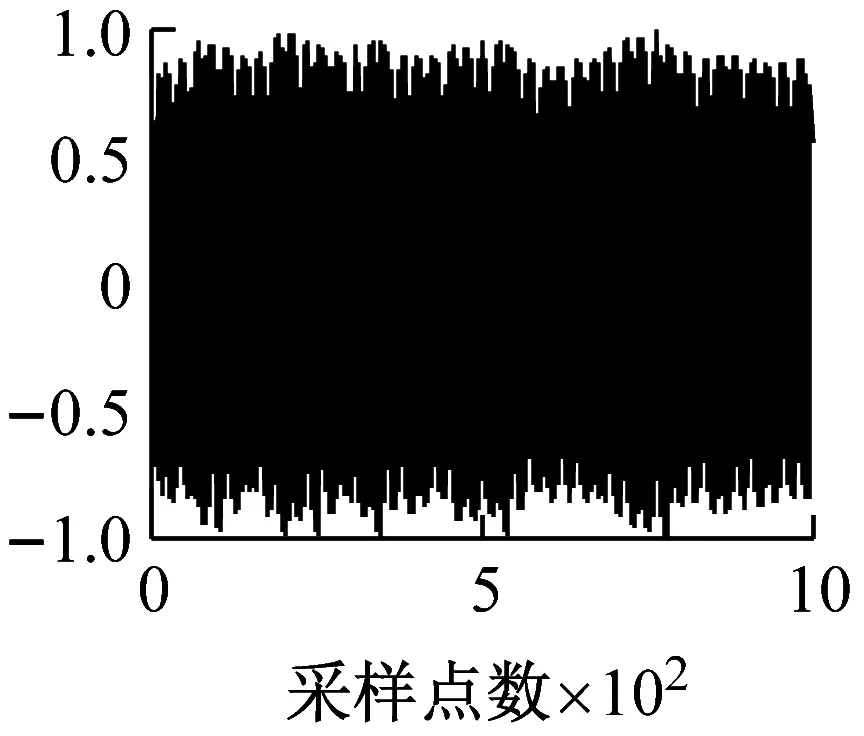
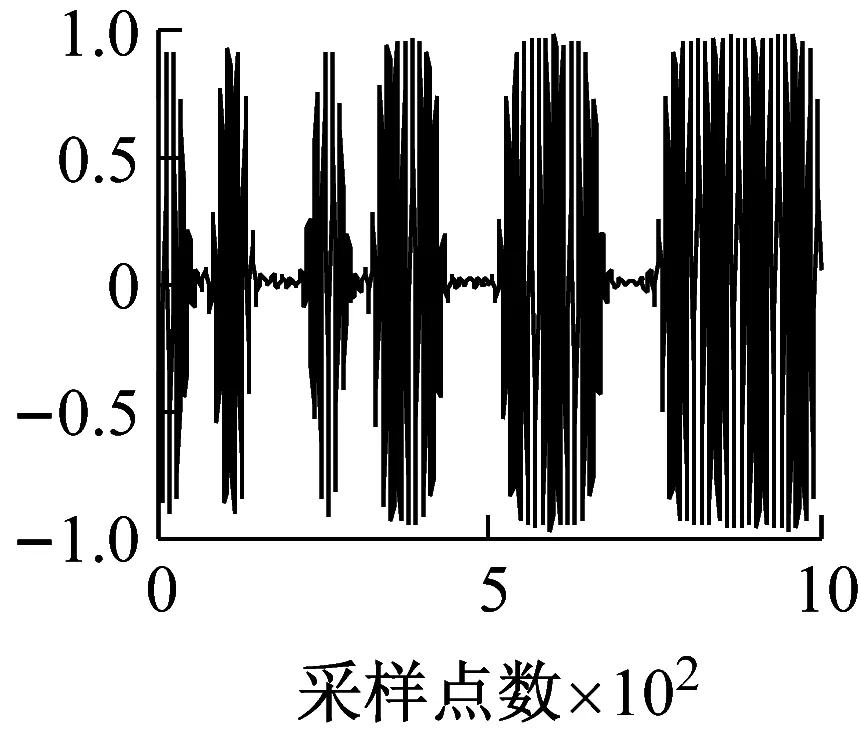
2.3 两种算法比较

3 结 论

