基于风洞试验模型的跨声速颤振研究
侯良学, 张 戈, 刘 南, 王 冬, 钱 卫, 杨希明
(1. 中国航空工业空气动力研究院,沈阳 110034; 2. 高速高雷诺数气动力航空科技重点试验室,沈阳 110034,3. 大连理工大学 航空航天学院,辽宁 大连 116024)
在跨声速区,由于压缩性和气动非线性的影响,飞行器的颤振速压边界一般降低较大,颤振边界随马赫数的变化曲线会呈现出所谓的跨声速“凹坑”现象,最小临界颤振速压值通常出现在跨声速范围。大量的民用和军用运输机又恰恰在跨声速区域巡航,军用战斗机也需要在跨声速区域保持足够的操纵能力。因此跨声速颤振特性研究在飞行器的研制过程中占据非常重要的地位。
针对跨声速颤振问题,20世纪50—60年代,美国国家航空咨询委员会(National Advisory Committee for Aeronautics, NACA)设计并建造了一座大型跨声速动力学风洞(Transonic Dynamic Tunnel, TDT),为跨声速颤振研究提供了试验支撑[1]。第一个颤振标准模型AGARD445.6机翼于1961年在TDT风洞开展了跨声速颤振试验并公布了大量的试验结果[2],目前三号弱模型已成为颤振计算程序的标准验证算例[3],但是该模型采用的实心木质材料外加中心打孔形式,无法进行准确的有限元建模。Ashley[4]利用数值计算手段对跨声速颤振中激波影响开展研究,结果表明:激波通常降低俯仰自由度的稳定性。Bendiksen[5]采用混合欧拉-拉格朗日方法研究了激波对跨声速颤振的影响。钱卫等[6]完成了某全机结构相似跨声速颤振风洞试验,是国内首次在跨声速风洞中完成全机颤振模型试验,同时进行了有限元模型结构模态分析和颤振计算仿真。陈千一等[7]针对某民机机翼跨声速颤振模型为研究对象,采用小扰动方程求解气动力,结合结构动力学求解颤振特性,得到了试验模型的颤振特性及变化趋势并与试验结果做了对比分析。谢亮等[8]采用CFD/CSD耦合时域颤振计算方法,对气弹标模AGARD445.6机翼和带边条平直翼进行了颤振计算研究。
相对于国外的跨声速颤振标模试验和计算研究,国内气动弹性计算基本以TDT风洞的AGARD445.6机翼为标模进行计算方法的验证,尚未开展过AGARD445.6模型的风洞试验研究。TDT进行AGARD445.6机翼颤振试验时,采用的木质材料,且模型开了较多通孔减小刚度,为使试验安全进行,试验速压极低。这也导致该标准模型不适合国内的跨声速风洞进行试验验证。而木质开孔的颤振标模在精确建模上存在一些问题,国内外进行颤振计算方法验证的AGARD445.6模型结构建模都采用简化的二维模型进行,会对计算的结果引入误差。本文从国内的跨声速风洞实际情况出发,设计加工了两套碳纤维复合材料的跨声速颤振试验标模,针对两套颤振试验标模,在航空工业气动院FL-3风洞开展了跨声速颤振试验研究,试验马赫数为0.59~0.98,研究了跨声速颤振的边界预测技术,得到颤振标模在试验马赫数下的颤振临界参数,同时基于CFD/CSD耦合的时域颤振计算方法开展了两套颤振试验标模的数值计算研究,试验结果与计算结果做了对比分析。研究结果表明,通过本文风洞颤振试验得到的颤振边界与CFD数值评估结果一致性较好,相互验证了跨声速颤振风洞试验方法和CFD/CSD耦合颤振计算预测方法的可信度。
1 试验模型和设备
1.1 试验模型
本项目研究颤振试验使用的标准模型共有两套:
模型1 依据国际上常用的气弹颤振标模AGARD4456的三号弱模型为基准,按照FL-3风洞速压运行范围设计的。模型几何尺寸为:展弦比1.644,稍根比0.652 9,1/4弦线机翼后掠角为45°,展长0.762 m,根弦长0.558 7 m,稍弦0.367 3 m,沿流向翼型为NACA65A004。模型采用45#钢梁架与复合材料蒙皮搭配的结构,其中钢梁架与蒙皮全面接触,内部空间填充聚氨酯发泡。试验模型重量11.3 kg。
模型2 按照FL-3风洞速压运行范围设计的一个舵翼模型。模型2采用对称翼型,结构形式为单梁+承力蒙皮的直轴舵面结构,肋板和蒙皮采用复合材料,梁分为内外两段,内段采用高强度铝合金7075材料,外段采用复合材料,内外段通过螺栓连接,蒙皮、梁、肋板围成的空腔中填充聚氨酯泡沫维型。模型2翼尖加铜管配重,提高其颤振边界,使模型2的颤振速压边界落在FL-3风洞的速压运行包线的中间位置,便于风洞颤振试验的实施。
两套试验模型在风洞试验段中的安装见图1。

(a) 模型1(b) 模型2
图1 颤振试验模型在风洞试验段中的安装图
Fig.1 Installation diagram of flutter test models in WT
1.2 模型支撑
本期试验两个颤振模型均采用FL-3风洞颤振半模专用安装机构安装,试验中不需要天平测力。模型1安装在FL-3风洞半模转窗上,模型与转窗之间留有3 mm的间隙,避免模型振动时与转窗发生摩擦,从而对模型系统的刚度阻尼产生影响,模型安装后攻角调平到零度。
模型1安装与模型2共用一个转窗,两套模型使用不同的连接件安装,模型2根部配有整流罩,同时具有模型自动防护装置。模型2自动防护装置原理是当模型发生异常时,系统自动通过气缸驱动模型卡板运动,限制止动销的位移,从而控制模型2的转动自由度,提高模型2的扭转刚度,模型2在转窗上各部分安装组件的相对位置见图2。
1.3 试验风洞
试验所用风洞为航空工业气动院FL-3亚跨超三声速风洞,试验段面积1 500 mm×1 600 mm。跨声速试验段上下壁开孔,左右壁为实壁,试验马赫数为0.3~1.2,前室最高压力0.4 MPa。
1.4 颤振试验数据采集处理系统
试验中采用了PXI动态数据采集系统,该系统是基于PXI总线的QTS2524动态测试系统,由CM4214放大器、CM4504低通滤波器、NI-PXI4472动态采集设备组成,系统共有24个通道,每个通道动态采样率51.2 kHz,动态采集精度0.2%。

图2 半模转窗及模型2安装组件
颤振试验采集和控制系统是基于PXI动态采集设备采用Labview软件环境开发的,兼容性较好。颤振试验采集和控制系统分前面板和后面板两部分,前面板为人机界面,便于观察信号的变化和设置各个参数等信息。后面板为程序设计界面,按照数据流的方式进行图形化编程。整个控制系统界面布局按照便于控制操作和便于吹风时实时监控来设计,界面左侧为模型振动信号观测区,右侧为试验操作控制区(见图3)。

图3 颤振试验控制软件界面
2 跨声速风洞突发型颤振标模试验
2.1 试验方法
试验Ma数范围:模型1为0.90~0.98,模型2为0.65~0.80。风洞试验时,采用固定来流M数阶梯增加速压q的吹风方式。试验中每个车次设置3个速压阶梯,每个速压阶梯下流场保持稳定10 s,在每一个速压阶梯下记录试验模型的振动信号,同时记录每个车次从起风到关车的全过程模型振动响应数据。为保证试验安全,每个试验马赫数首个吹风车次都需从风洞的速压下边界开始,逐渐增加试验速压。试验采用亚临界响应分析方法,通过模态参数外插方法预测颤振临界速压。
跨声速风洞试验中颤振边界的获取方法一般有两种:①在试验中直接吹到颤振发生;②通过事先设定速压台阶逼近颤振临界速压,然后借助亚临界响应分析来预测或外推颤振边界。前者更加直观准确,但风险极大、成本高、试验方案制定困难,而且不易确认颤振类型、颤振发生过程及颤振模态参数。相对来讲,亚临界响应分析方法具有风险小、成本低、易于各种技术指标量化等优势。亚临界响应分析方法是基于试验模型结构的亚临界响应测量,通过信号分析从系统动态响应中提取能刻画试验模型结构振动特征的信息,依此确定飞机的颤振特性。其试验流程是:①对试验数据截取有效数据,去除预趋势项和直流分量,并根据所感兴趣的频率段设置带通滤波器进行数字滤波等预处理;②去除经过预处理后的试验数据中由风洞气流噪声、电子信号等引起的随机干扰响应,保留由初始条件引起的有效物理振动响应数据,再选取合适的模态辨识方法求得模型各阶模态参数。高速风洞颤振试验中会有一组多个逐渐接近临界颤振速压的速压阶梯,可以构造出一组多个逐渐接近临界值的结构模态参数。这些模态参数反映了模型的稳定性变化情况,通过拟合这些模态参数就可外推出颤振临界速压。参考国内跨声速颤振试验的预测方法[9],本文试验中采取了PEAK-HOLD方法来外推颤振边界。相对于阻尼比、Routh判据和Jury判据等方法,PEAK-HOLD方法具有较高的鲁棒性和可靠性。亚临界响应分析具体流程框图,如图4所示。
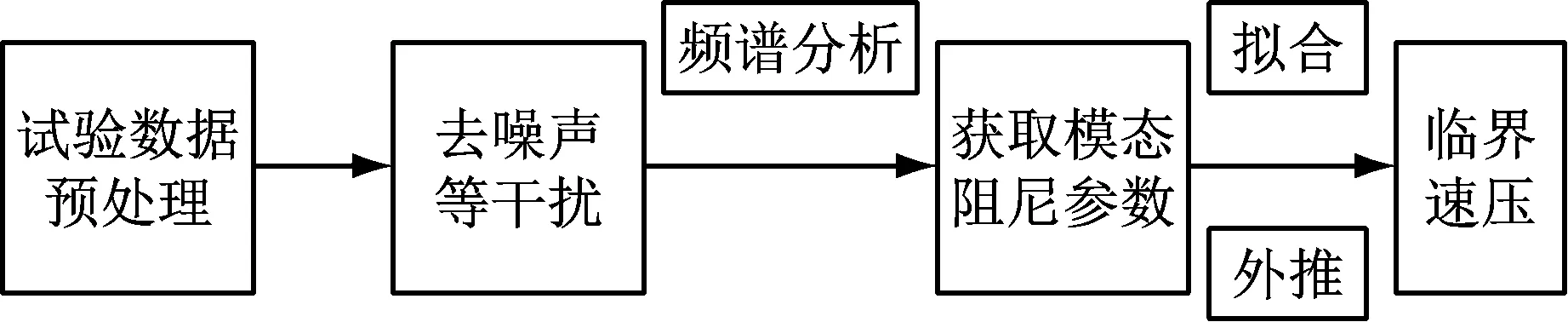
图4 亚临界响应分析流程图
PEAK-HOLD方法根据测量所得的颤振试验模型在亚临界区域的主要振动模态功率谱幅值,按照功率谱幅值的峰值倒数1/A来外推,得出峰值倒数等于零时对应的风洞速压q及模型振动频率f,即为颤振试验模型的临界速压边界和临界频率边界。
2.2 试验结果分析
通过本次风洞试验,共获得2个两套试验模型在6个不同马赫数下的颤振边界数据。图5给出了模型1在Ma=0.96时某车次试验时域曲线,曲线图中包含试验速压阶梯曲线,颤振模型中加速度计信号曲线和弯扭应变片信号曲线。图6(a)给出了模型1在Ma数0.96试验速压64 kPa、66 kPa和67.5 kPa下的模型振动信号的频谱分析图,图6(b)是根据Ma=0.96时所有试验速压的颤振试验数据频谱分析结果,按照亚临界响应方法预测颤振边界的外插曲线。曲线中的A值是根据前面所叙述的数据分析方法,通过频谱分析得出的每个阶梯速压下模型振动信号功率谱密度的主频幅值。从模型时域振动信号上看,试验速压增大时,振动信号的幅值有所增大,但不太明显,对模型振动信号进行频谱分析后,从频域结果则可以看出模型振动的主频幅值有明显变化,随试验速压的增大,模型振动主模态幅值有增大的趋势。
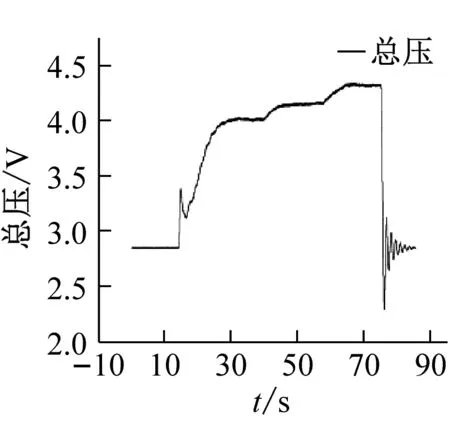
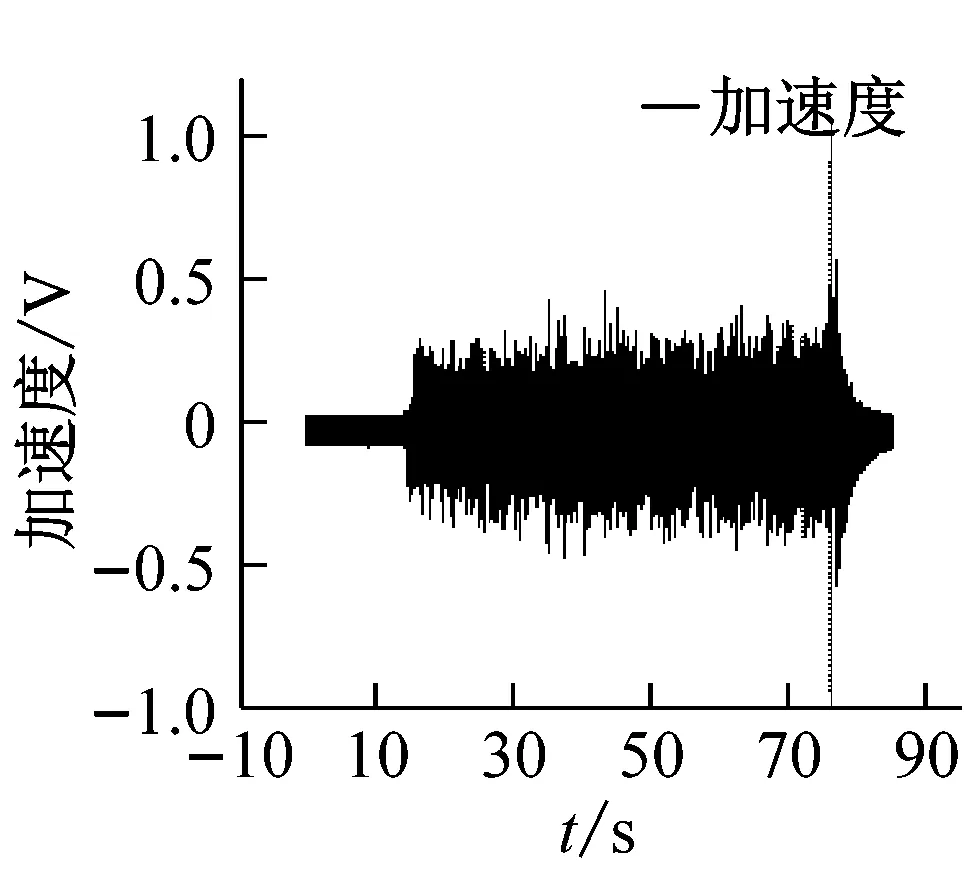
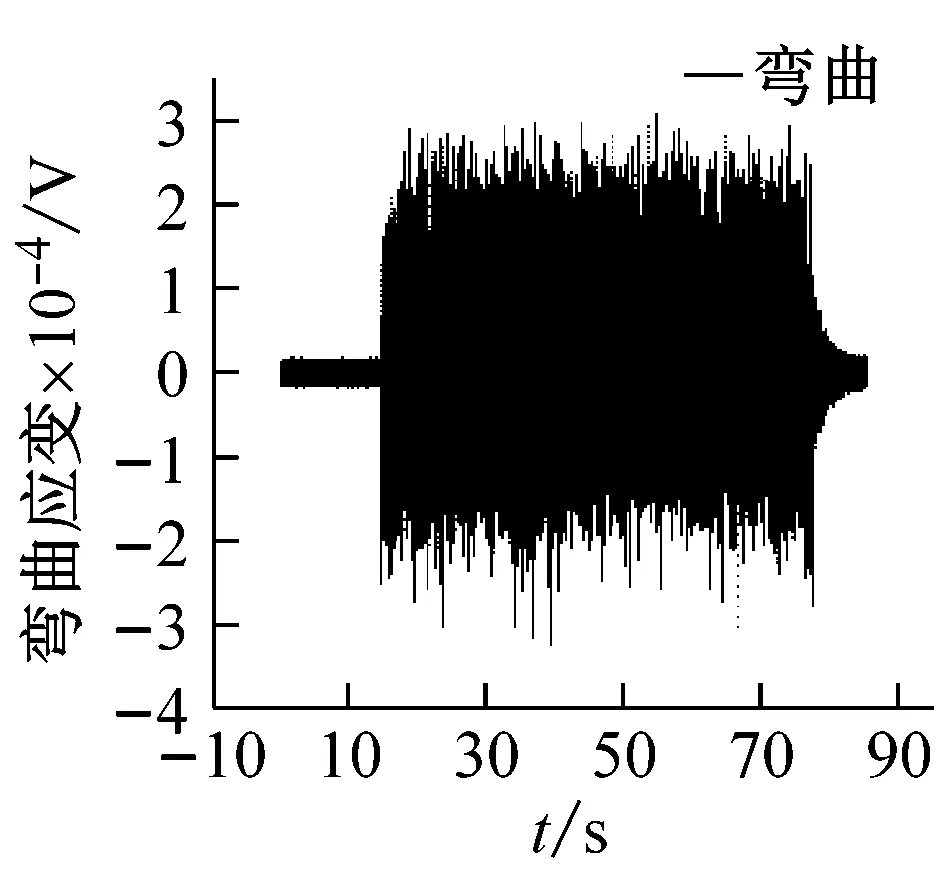
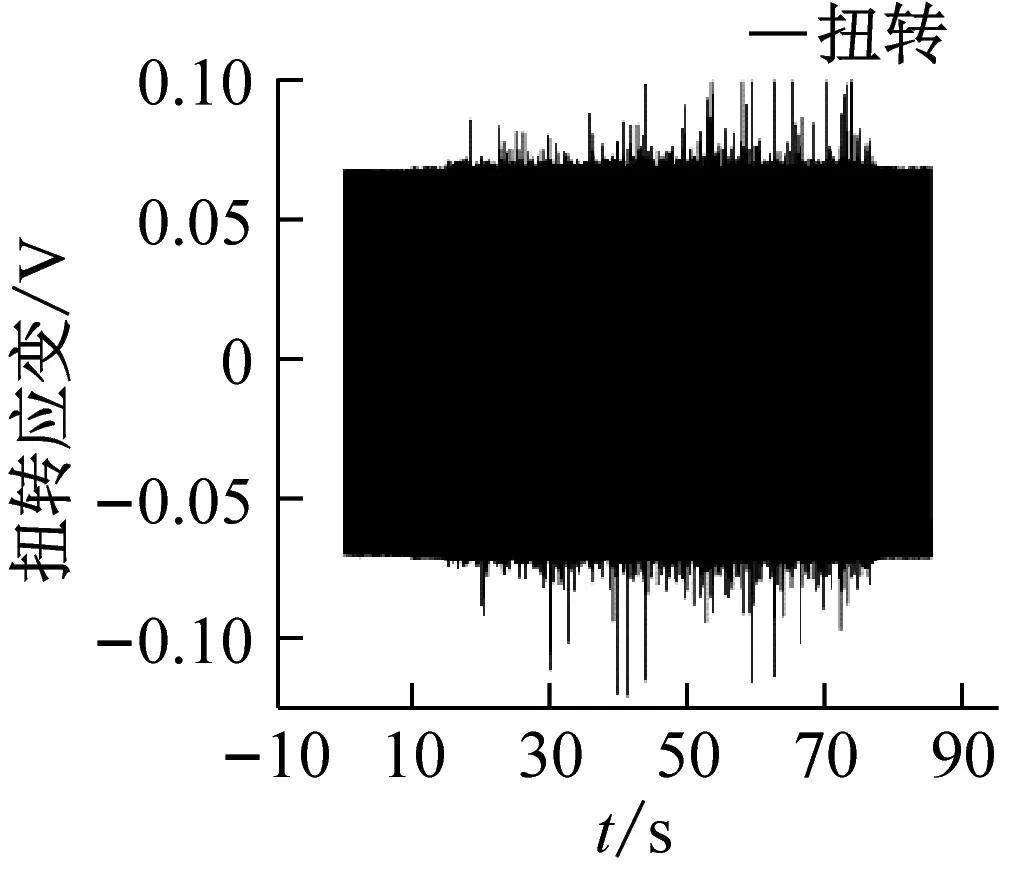
图5 模型1试验中振动时域曲线
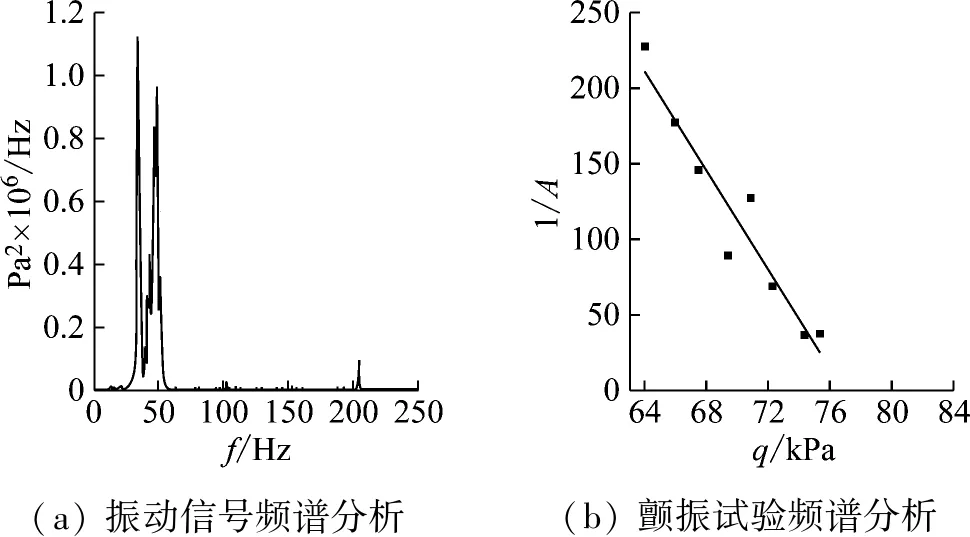
(a) 振动信号频谱分析(b) 颤振试验频谱分析
图6 模型1颤振边界外插曲线
Fig.6 Interpolation curve of test model 1 flutter boundary
通过相同的方法,通过本次试验获得了不同试验Ma数的模型1颤振速压和颤振频率。表1给出了本期试验的结果,获得了模型1在Ma数0.92、0.96、0.97下的颤振边界值和模型2在Ma数0.8、0.65和0.72下的颤振边界值。对于模型1的试验结果可以得出一些规律,从试验Ma数0.92~0.97,可以看出颤振边界变化从减小到增大,在Ma=0.96时,颤振边界值最低。
AGARD445.6机翼亚跨声速区域的颤振特性也表现为颤振边界随马赫数的增加先减小后增大的趋势,在马赫数0.96附近达到最低点。可见模型1与设计原型AGARD445.6机翼的颤振特性是一致的,也证明了模型1试验结果规律的合理性。
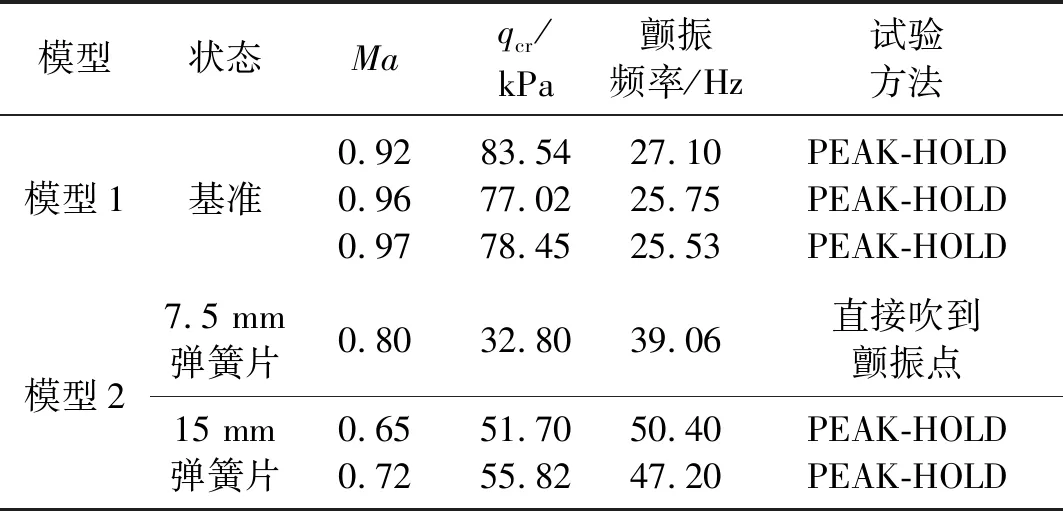
表1 颤振边界风洞试验结果
3 基于CFD/CSD耦合的颤振标模计算
对于本文研究颤振试验模型,同时开展了详细的数值计算研究。采用了频域方法[10]和CFD/CSD耦合时域颤振计算方法分别进行了颤振试验模型的数值计算研究。
3.1 CFD/CSD耦合颤振计算方法
基于NS方程颤振计算主要有三个关键环节:非定常气动力计算,结构运动方程计算和气动与结构间载荷和位移的数据传递。
3.1.1 结构运动方程
考虑颤振试验模型的变形为小变形假设,采用线性的模态叠加法描述结构变形,模型变形可表示为
(1)
式中:nm为所取得结构模态阶数;hi为第i阶模态振型;qi为第i阶广义位移。
应用拉格朗日方程,两套颤振试验模型的运动方程可以写为下述形式
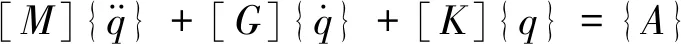
(2)
式中:[M]为广义质量矩阵;[G]为广义结构阻尼矩阵;[K]为广义刚度矩阵,其值与模型结构和质量分布相关,可通过结构有限元分析软件或试验获得;{A}为广义气动力。
用龙格-库塔方法作时间推进求解结构运动方程,在每推进一个时间步长时,由N-S方程计算的压力分布提供所需的广义气动力载荷。
3.1.2 非定常气动力计算
CFD/CSD耦合颤振数值计算中非定常气动力采用可压缩、非定常N-S方程求得,其积分形式为
(3)
式中:Q=[ρ,ρu,ρv,ρw,ρe]T为解向量;∂V为流体域控制体V的边界。n为边界外法向矢量,矢通量F可以分解为对流矢通量Fc和黏性矢通量Fv两部分。
F=Fc+Fv
(4)
采用有限体积法、双时间推进求解非定常N-S方程,湍流方程采用S-A一方程湍流模型。
3.1.3 动网格方法及数据交换
采用径向基函数(Radial Basis Function,RBF)插值方法建立气动和结构交界面上力和位移的数据传递关系,该方法不依赖模型,只需要离散点之间的一个关系式,适用于任意形状模型的数据交换,可以应用于任意点的数据传递。同时RBF方法也用于本文的网格变形。
3.2 计算网格
颤振计算中非定常气动力采用NS方程计算,气动计算网格采用非结构网格形式,并在附面层内进行了加密,同时对网格的计算收敛性进行了分析研究,兼顾计算效率和精度确定了合适的网格参数(见图7)。模型1计算所用网格空间首层高度为4×10-5m,增长率1.25,网格节点数量为23.25万;模型2计算所用网格空间首层高度为5×10-5m,增长率1.2,网格节点数量19.8万,模型2与整流罩采用光顺方法连接。
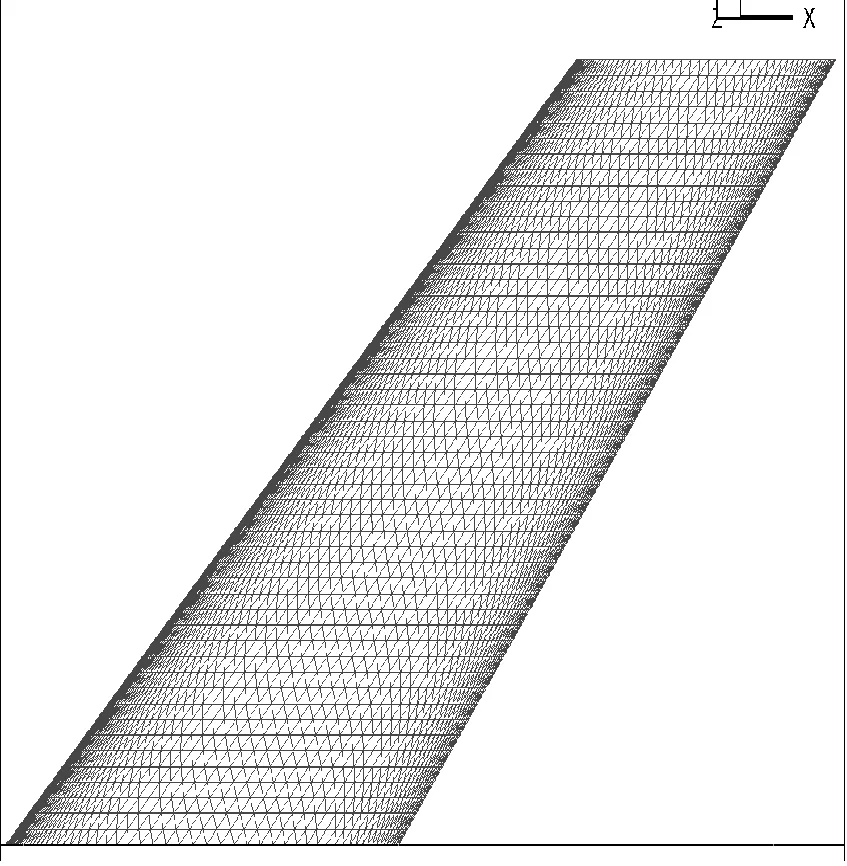

图7 颤振试验模型气动网格
3.3 结构模态
试验模型的结构模态数据通过地面振动试验(Ground Vitration Test, GVT)获取。GVT试验采用西门子LMS Test.lab模态测量软件系统,激振力锤采用江苏联能公司产品,加速度传感器采用PCB公司的ICP(Integrated Circuits Piezoelectric)压电加速度传感器。试验方法使用锤击法。通过GVT试验得到的两套颤振试验模型的模态振型,见图8和图9。频率见表2,表中的模型频率按GVT测量获取的一弯频率做了无量纲化处理。通过表2可知,GVT试验的结果与有限元计算分析的结果吻合很好,保证了结构模态参数的准确度。
3.4 计算结果及分析
对试验模型进行GVT测试得到的结构模态数据作为输入条件应用到颤振试验模型的数值计算中,分别采用ZAERO软件计算(频域方法)和CFD/CSD耦合方法计算(时域方法)研究了两套颤振试验模型的颤振特性。图10和图11分别给出了模型1和模型2的计算结果与试验结果对比曲线。


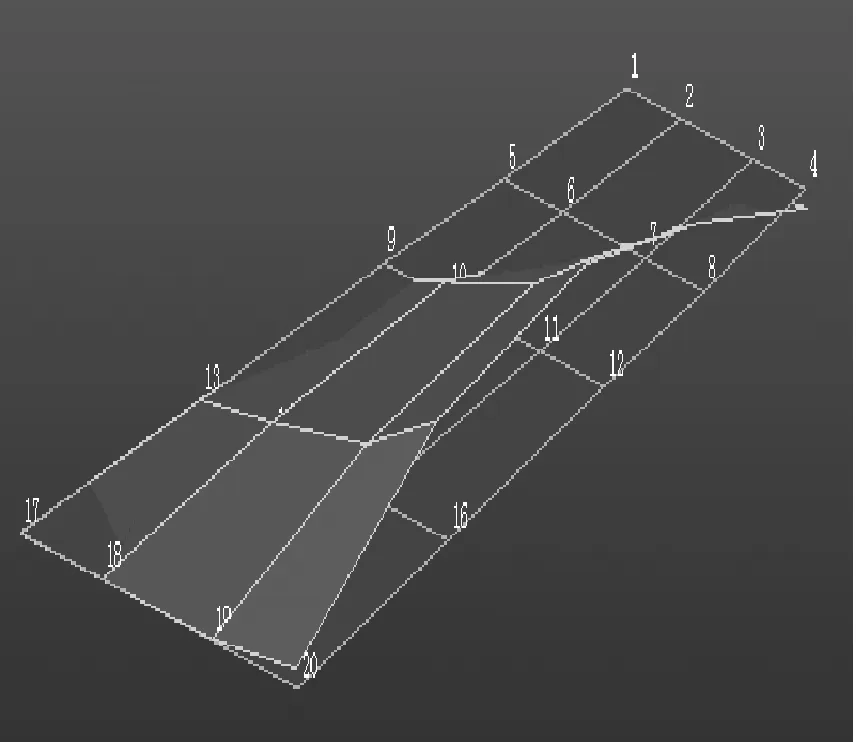
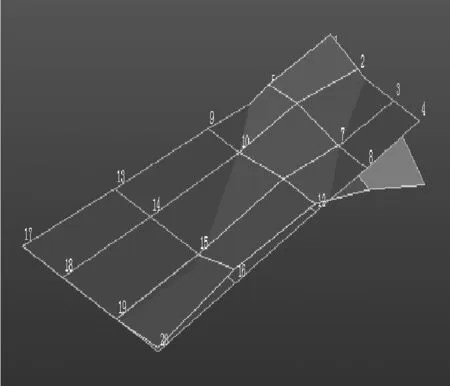
图8 模型1前四阶结构振型

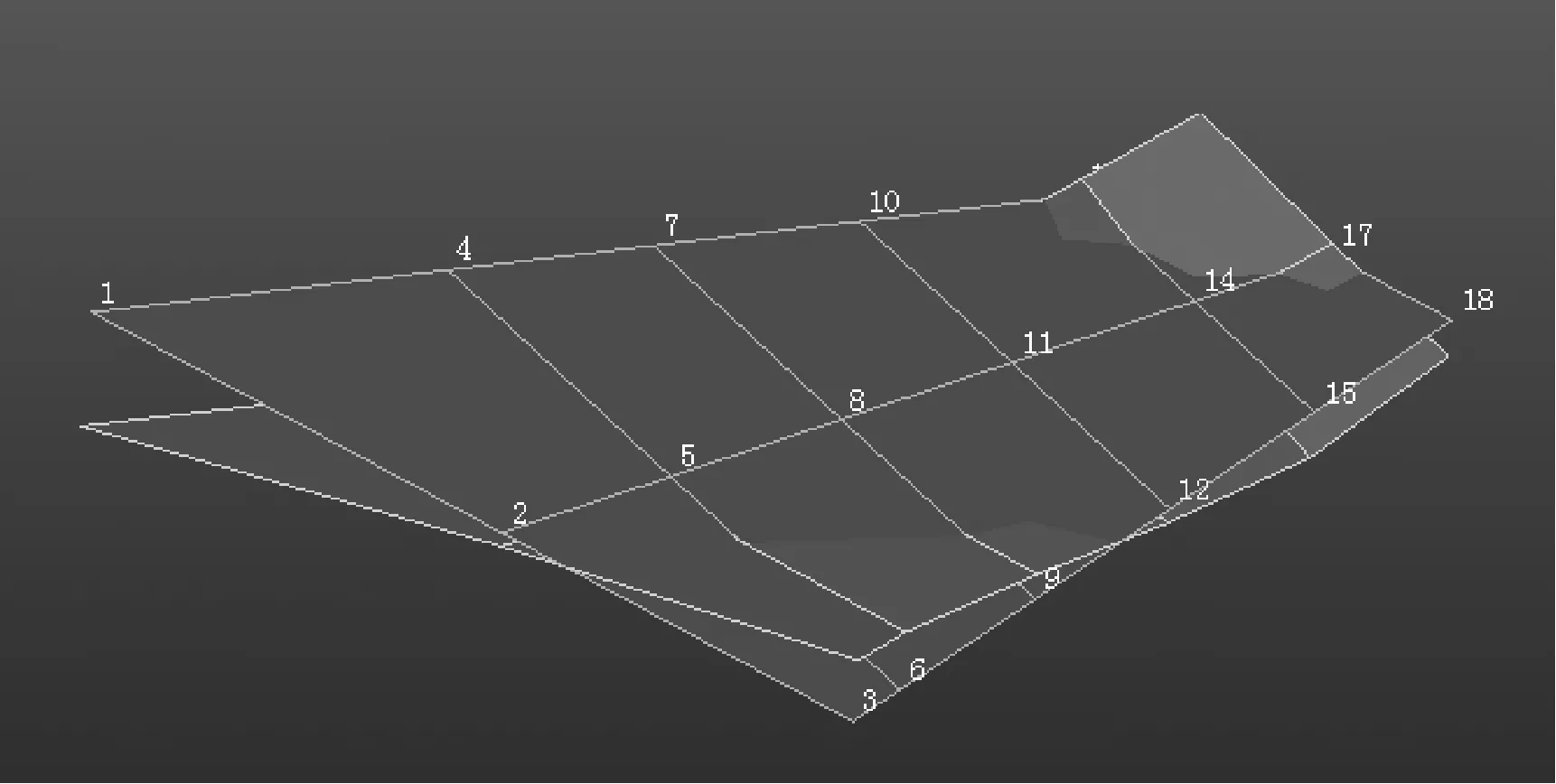
图9 模型2前三阶结构振型
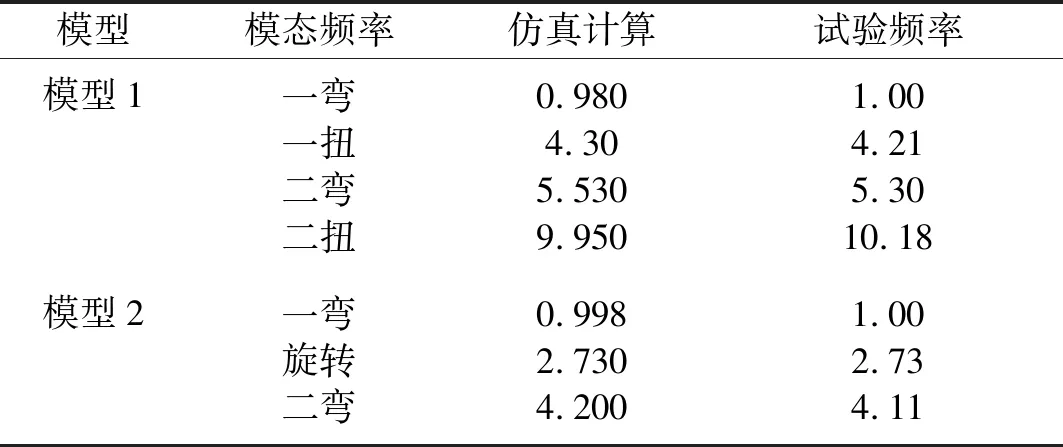
表2 结构模态参数计算与试验结果(无量纲化)
从图10可知,对于模型1时域和频域两种计算方法得出的颤振边界曲线趋势是很一致的,也与原型机翼AGARD4456颤振特性一致。随马赫数的增大,颤振速压先降低后增大,出现跨声速“凹坑”现象,凹坑位置基本相同,最低颤振点大约在Ma数0.96附近出现,颤振频率对比曲线显示了与颤振速度相同的变化规律。与风洞试验结果综合对比,风洞试验和计算获得的颤振边界不仅在趋势规律上一致,在量值上吻合也很好,三个试验马赫数下数值计算结果与试验结果平均误差小于5%,证明了试验结果和计算结果的合理性和高可信度。
模型2计算结果显示CFD/CSD耦合计算的颤振计算结果与线化方法的结果差异较大,CFD/CSD耦合计算的颤振速压及频率都要明显低于线化计算的结果。图11中结果对比曲线也显示CFD/CSD耦合颤振计算的结果更加靠近风洞试验结果,误差小于10%。考虑到模型2带转轴的舵翼构型在跨声速区域气动力的非线性影响更为明显,激波附面层的影响不可忽略,因此对于模型2的气动力线化计算结果与CFD/CSD耦合计算结果存在较大的差异,通过与风洞试验结果的对比也可看出,CFD/CSD耦合颤振计算的结果更接近于颤振试验的数据,CFD/CSD耦合颤振计算方法更适合模型2的跨声速颤振特性的数值计算研究。
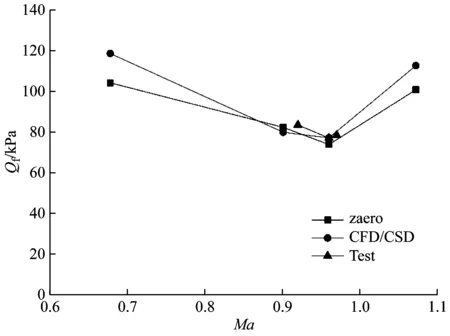
(a) 颤振速压边界曲线
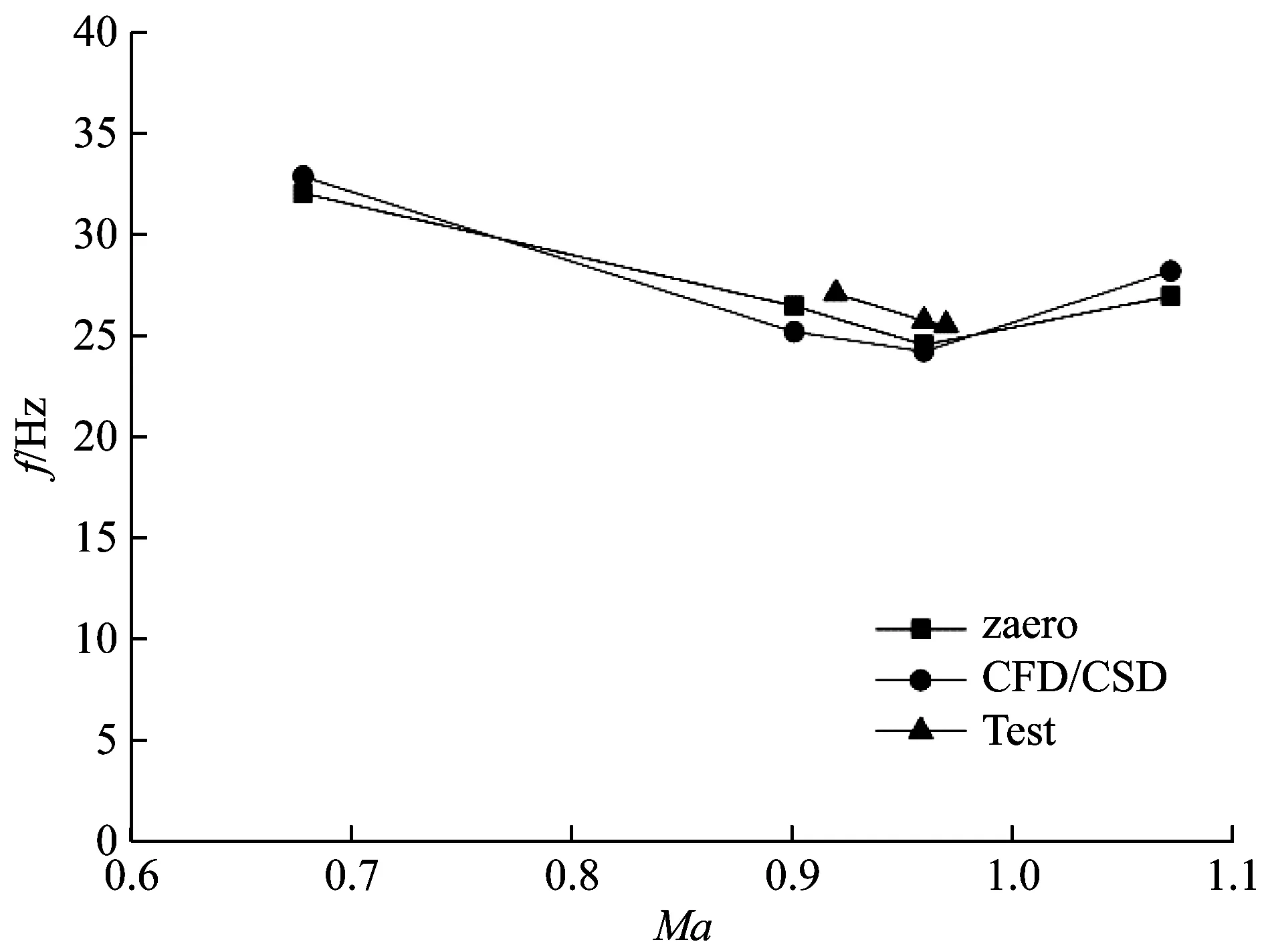
(b) 颤振频率边界曲线

(a) 颤振速压边界曲线
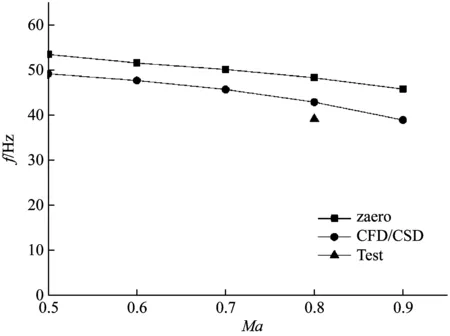
(b) 颤振频率边界曲线
4 结 论
本文以FL-3跨声速风洞为平台,通过两套跨声速风洞颤振试验标模的数值计算和试验研究,建立了跨声速突发型颤振的试验技术和数值计算方法。同时进行风洞试验和计算验证,通过本文工作得到以下结论:
(1) 建立两套跨声速风洞颤振试验标模,通过试验和数值计算,获取了颤振标模的结构动力学参数和模型的跨声速颤振特性。
(2) 采用PEAK-HOLD亚临界响应预测分析方法,建立跨声速突发型颤振边界的风洞试验预测技术,并通过风洞试验验证。
(3) 通过CFD/CSD耦合时域颤振计算方法,计算评估了两套颤振试验模型的跨声速颤振边界,计算结果与试验结果一致性较好,相互验证了试验方法和数值计算手段的可信度。

