基于JC法的近场地震作用下钢筋混凝土高墩塑性铰形成概率分析

赵金钢, 占玉林, 贾宏宇, 李 晰, 谢明志

(1. 贵州大学 土木工程学院, 贵阳 550025; 2. 西南交通大学 土木学院, 成都 610031;3. 陆地交通地质灾害防治技术国家工程实验室, 成都 610031)

我国西部地区处于亚欧板块与印度洋板块的交界区域，地震断裂带十分活跃，近年来先后发生了汶川地震、玉树地震、芦山地震和九寨沟地震等多起7.0级以上的大地震，表明我国已经进入了地震活跃期。但是，在现有的科学技术水平下，地震几乎是不可预测的，因此应采用合理的抗震设计方法，以尽可能地降低人员伤亡和经济损失，其中延性抗震是当前广泛采用的抗震设计方法。延性抗震是指：使结构选定部位在地震荷载作用下发生反复弹塑性循环变形，消耗大量的地震动输入能量，降低结构地震响应的一种抗震设计方法。桥梁结构通常将墩柱作为延性设计构件，但是《公路桥梁抗震设计细则：JTG/T B02-01—2008》[1]中给出的墩柱塑性铰区域仅适用于墩高不超过40 m的中低墩。对于高度超过40 m的高墩，墩身的质量和柔度较大，高阶振型对桥梁结构的地震响应影响较大，使其塑性铰形成区域与中低墩有较大区别。因此，关于高墩的塑性铰形成和分布规律急需研究。

当前，国内外学者对高墩桥梁的塑性铰形成规律进行了研究，Ceravolo等[2]通过对主墩高度为90 m的多跨连续梁桥进行动力非线性分析，研究表明在桥墩高度的1/3处会产生塑性铰；梁智垚等[3]研究表明，高墩在墩身中部及墩底同时形成塑性铰，塑性区随地震激励的增强而扩展，且高墩与中低墩塑性铰形成和发展方式完全不同；夏修身等[4]对铁路高墩进行了弹塑性地震反应分析，研究表明高墩在墩底和墩身中部区域均可能形成塑性铰，一定地震动强度下墩底塑性铰区域位置相对明确，而墩身中部塑性铰区域受地震动影响较大，并且潜在塑性铰区在0.28倍～0.46倍墩高范围内；何钦象等[5]对某高墩大跨连续刚构桥进行抗震分析研究表明，当地震达到一定烈度时，桥墩系梁处也会出现塑性铰；卢皓等[6]研究表明高墩桥梁在强震作用下，除在墩底产生塑性铰外，由于第二阶振型的贡献还会在墩身中上部产生形成塑性铰区域；陈旭等[7]采用增量动力分析法研究表明，由于高墩墩身高阶振型的显著影响，在强震作用下沿墩身有可能出现多个塑性区域。综上所述，国内外研究成果表明：地震荷载作用下，高墩墩底和墩身中部区域均会形成塑性铰，但是当前研究多是采用多条地震波对高墩桥梁进行增量动力分析(Incremental Dynamic Analysis, IDA)后，得出是否形成塑性铰的确定性结论，而未考虑桥墩本身材料特性和截面尺寸等参数的随机性对高墩动力响应和塑性铰形成临界指标的影响，降低了分析结果的精度。并且我国西部地区存在多条活动断裂带，西部地区的高墩桥梁承受近场地震动荷载作用的概率较大，但是当前对于近场地震动荷载作用下钢筋混凝土高墩塑性铰形成和分布规律的相关研究尚开展较少。

因此，本文以高度为90 m的某钢筋混凝土高墩为研究对象，采用支持向量机算法对考虑墩身参数随机性的顺桥向和横桥向截面等效屈服曲率值的概率分布类型和统计参数进行研究，同时采用OpenSees软件对顺桥向和横桥向近场地震动作用下的钢筋混凝土高墩进行IDA，同时引入JC法对高墩动力响应进行当量正态化后，分别计算顺桥向和横桥向近场地震动作用下的高墩截面塑性铰形成概率，并与只考虑近场地震波随机性的高墩塑性铰确定性计算结果对比，研究钢筋混凝土高墩塑性铰分布规律。

1 钢筋混凝土高墩有限元模型

1.1 工程背景

西部山区某高速公路桥梁，上部结构采用6×40 m的预应力混凝土简支T梁，并设有墩高为45～90 m的5座钢筋混凝土桥墩，本文选择其中高度为90 m的空心薄壁钢筋混凝土高墩为依托工程实例，研究分析近场地震作用下钢筋混凝土高墩的塑性铰形成规律，高墩立面布置如图1所示。实例钢筋混凝土高墩采用空心变截面形式，壁厚为60 cm，横桥向宽度由墩底到墩顶按1∶50的比例从6.4 m渐变为2.8 m，顺桥向宽度采用固定尺寸为5 m；墩底和墩顶的1.5 m范围内为实心段，并且在墩身中部设置两道间隔为29m的横隔板，钢筋混凝土高墩采用C40混凝土和HRB400钢筋建造。由于横隔板将高墩划分为三段，为表述方便，沿墩高方向将高墩命名为Ⅰ号段、Ⅱ号段、Ⅲ号段，如图1中所示。

1.2 有限元模型建立

采用OpenSees软件建立高墩的三维有限元模型，因为地震作用下，上部结构的惯性力主要由桥墩承受，使得墩身产生较大弯矩，进入弹塑性变形，所以本文采用基于柔度法的弹塑性梁柱单元(Nonlinear Beam Column)结合纤维截面(Fiber Section)模拟高墩弹塑性力学行为。由于箍筋的约束作用，使得高墩截面分为无约束混凝土、约束混凝土和钢筋三部分(图1中给出了高墩截面的划分示意图)，其中无约束混凝土和约束混凝土采用Concrete02模型模拟，Concrete02模型是基于Scott和Park等修正的Kent-Park单轴混凝土本构模型[8]，图1中给出了Concrete02模型的应力-应变关系曲线，由于当前仅有《日本公路桥梁抗震规范》[9]对空心矩形截面的箍筋约束混凝土本构关系给出了明确规定，因此本文依据《日本公路桥梁抗震规范》计算确定高墩实心矩形截面和空心矩形截面的约束混凝土强度fpc和最大压应力对应的应变εc0；钢筋的材料特性采用基于Giuffré-Menegotto-Pinto Model with Isotropic Strain Hardening模型[10]的Steel02模型模拟，其应力-应变关系如图1中所示。

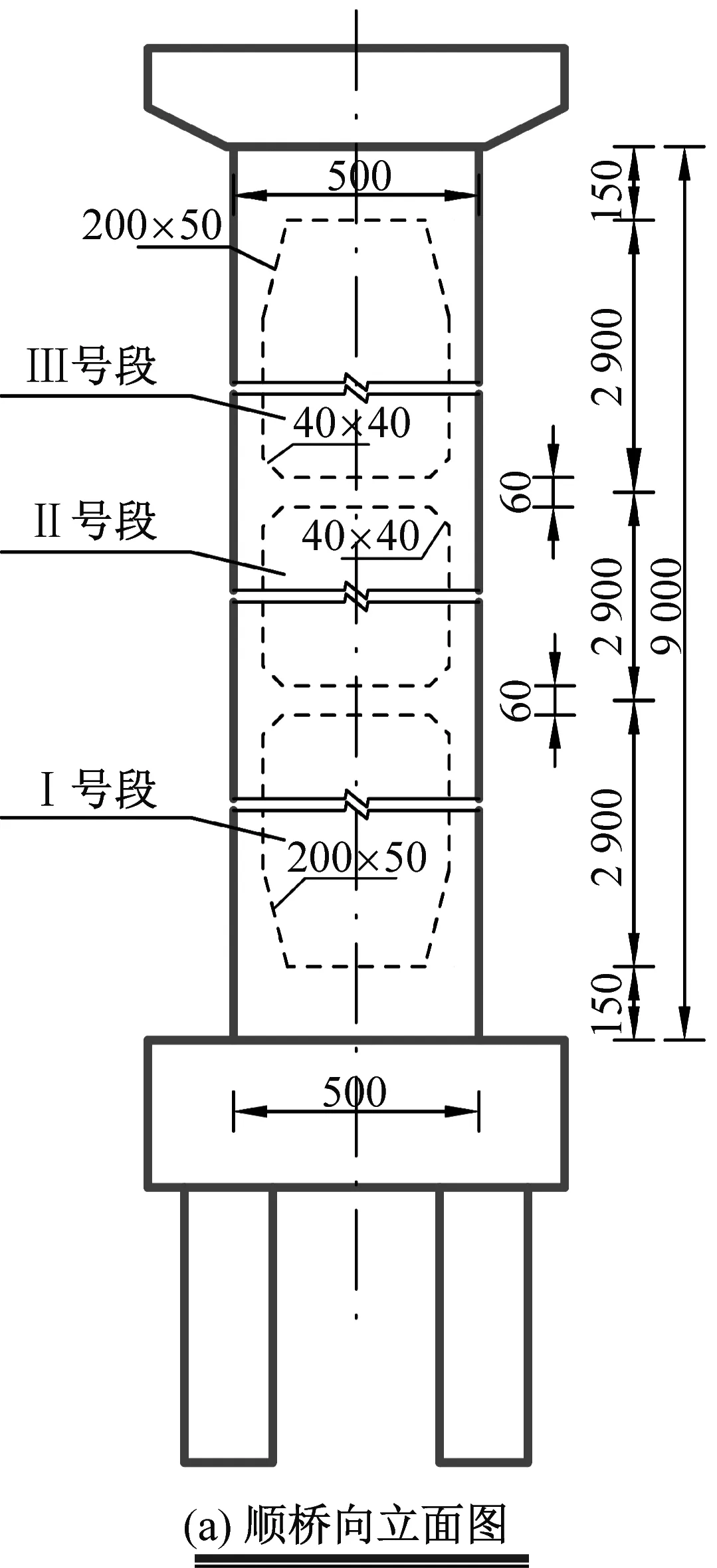
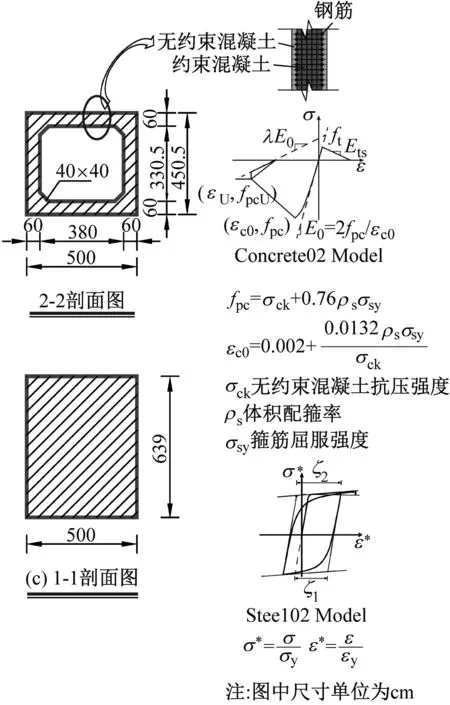
图1 高墩立面图

Fig.1 Elevation of the high-pier

为全面分析钢筋混凝土高墩的塑性铰区域形成规律，本文将高墩离散为179个单元，单元长度为0.4～0.6 m(每个单元均采用四个高斯积分点)，并取各单元中点处的截面尺寸作为单元尺寸，其中横隔板、墩顶和墩底实心段采用实心矩形纤维截面模拟，墩身空心段采用空心矩形纤维截面模拟；在高墩有限元模型的各节点上施加相应节段质量的点质量以模拟墩身质量分布，并将一跨简支梁的自重和二期恒载等效为集中质量施加在高墩有限元模型墩顶节点，以考虑上部结构对高墩地震响应的影响；由于高墩为长细比较大的高耸结构，并且在地震荷载作用同时承受轴力和水平力的作用，导致高墩结构产生二阶效应，因此本文在进行动力非线性分析时考虑P-Delta效应以真实地反映高墩结构在地震动荷载作用下的内力和变形；由于高阶振型对高墩地震响应影响较大，因此采用0.9T1和0.25T1(T1为高墩基本周期)对应的结构振型圆频率计算Rayleigh阻尼[11]；由于该桥桥位处地质条件良好，因此采用固结约束模拟墩底边界条件。

2 随机参数选取与近场地震波的确定

由于实际工程中存在诸多不确定性因素，使得钢筋混凝土高墩的地震响应和塑性铰形成临界指标均存在随机性，为全面分析近场地震动作用下，钢筋混凝土高墩的塑性铰形成概率和分布规律，本文考虑了桥墩本身参数和近场地震波的不确定性对钢筋混凝土高墩地震响应和塑性铰形成指标随机性的影响。

2.1 桥墩本身随机变量选取

桥墩本身的材料特性、截面尺寸、结构质量和阻尼比等的随机性均会导致钢筋混凝土高墩动力响应和塑性铰形成临界指标产生随机性，并且文献[12]中研究表明，不考虑结构本身的随机性会低估结构的潜在地震危险。因此，本文选取了混凝土容重、混凝土抗压强度、截面高度等11个随机变量，并确定了其概率分布类型和分布特征，如表1[13-18]所示。

2.2 近场地震波的确定

地震动的不确定性是影响钢筋混凝土高墩动力响应不确定性的重要因素，因此选取恰当的近场地震波是钢筋混凝土高墩塑性铰形成概率分析的重要环节。速度脉冲是近场地震动明显区别于远场地震动的典型特性[19]，简单的脉冲模型通常将脉冲参数简化为速度脉冲幅值和周期等极少数参数的函数，有利于研究结构在脉冲作用下的响应规律和破坏机理。因此，本文选用速度脉冲幅值和周期作为表征近场地震波的特征变量，并采用MATLAB软件的统计工具箱对Shahi等[20]确定的243条近场地震波的速度脉冲幅值和周期进行统计分析，得出速度脉冲幅值和周期均服从广义极值分布，概率拟合曲线如图2所示。综合考虑计算成本和准确性，本文选取了50条近场地震波，其速度脉冲幅值范围为23.74～264.11 cm/s、周期范围0.67～12.43 s，脉冲幅值和周期如图2中所示，阻尼比为5%、峰值加速度为1.0g时所选取近场地震波的绝对加速度反应谱如图3中所示。由图2和图3可见，本文所选取近场地震波的速度脉冲幅值和周期包含范围较广，基本能反映近场地震波的特性，并且具有较好的偶然不确定性。

表1 随机变量参数

图2 速度脉冲幅值和周期概率密度拟合曲线

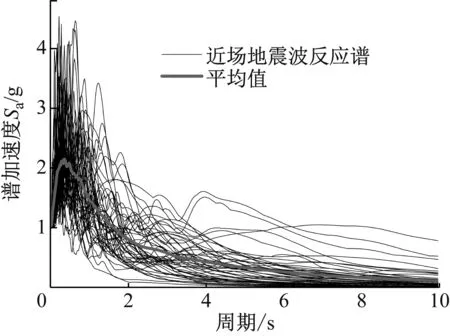
图3 近场地震波反应谱曲线

3 塑性铰形成临界指标及概率分布形式确定

3.1 塑性铰形成临界指标

地震动荷载作用下的高墩破坏一般属于弯曲破坏，并且破坏过程中会产生较大的塑性变形使得高墩保护层混凝土剥落、纵向钢筋屈服，高墩的破坏过程与塑性铰的形成、发展和失效过程相对应。墩柱塑性铰区的形成始于最大弯矩截面纵筋的屈服，并在最大弯矩截面附近形成一个塑性变形区域，随着荷载和弯矩的增加，塑性铰区范围不断扩大，塑性转角也迅速增大，当转角达到墩柱塑性铰的极限转动能力时，截面达到极限弯矩[21]。我国现行《公路桥梁抗震设计细则:JTG/T B02-01—2008》给出了轴压力作用下桥梁墩柱潜在塑性铰区的截面理想弹塑性弯矩-曲率(M-φ)曲线，如图4所示。

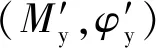
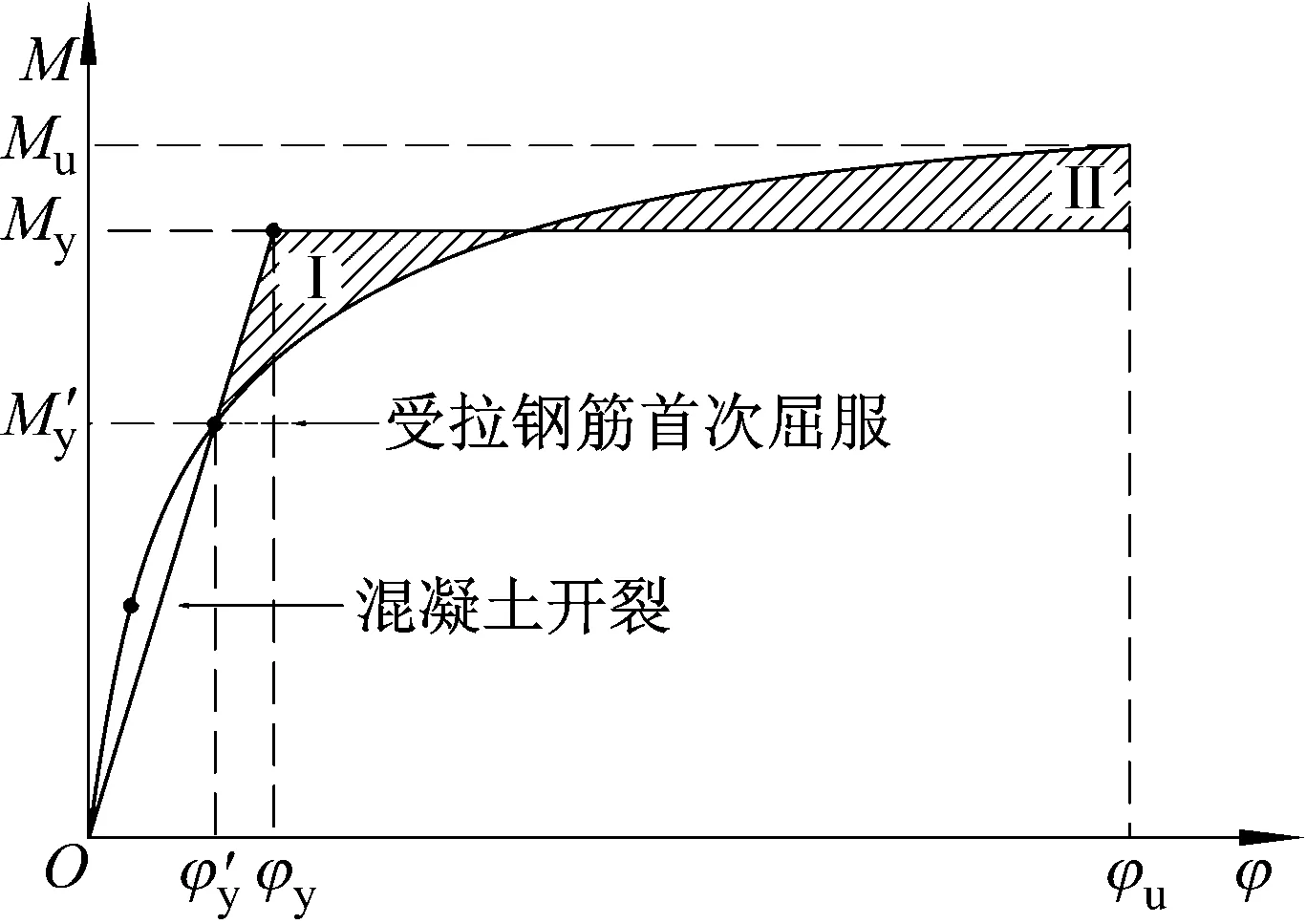
图4 截面弯矩-曲率关系

3.2 等效屈服曲率概率分布形式确定

由于桥墩本身材料特性和截面尺寸等具有随机性，使得钢筋混凝土高墩横截面等效屈服曲率φy值产生随机性，但是当前进行高墩塑性铰形成分析时，多未考虑等效屈服曲率的随机性。因此，本文取表1中的前10个参数作为随机变量计算依托工程实例的钢筋混凝土高墩各截面顺桥向和横桥向的等效屈服曲率值，并引入具有良好小样本学习和泛化能力的支持向量机算法结合蒙特卡罗法(Suppot Vector Machine-Monte Carlo Method, SVM-MCS)对各截面顺桥向和横桥向等效屈服曲率的概率分布形式进行分析研究。

根据文献[22]，采用SVM-MCS法按如下流程确定高墩各截面顺桥向和横桥向等效屈服曲率的概率分布形式：

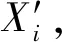
支持向量机的显式函数为

(1)

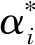
为分析各随机变量的离散性对截面等效屈服曲率响应的贡献程度，结合回归拟合得到的支持向量机显式函数式(1)，得到截面等效屈服曲率敏感性系数计算公式

(2)

式中：xj为第j个随机变量；μxj为第j个随机变量的均值；σxj为第j个随机变量的均方差。

按照上述流程，本文采用SVM-MCS法研究表明钢筋混凝土高墩各截面顺桥向和横桥向等效屈服曲率均服从正态分布，限于篇幅，本文仅列出了图1中1-1截面和2-2截面的顺桥向和横桥向等效屈服曲率概率分布图，如图5所示。为确定应用SVM-MCS法预测截面等效屈服曲率的准确性，本文采用拉丁超立方采样法(Latin Hypercube Sampling, LHS)对随机变量抽取50个样本点Xj(j=1,2,…,50)，同时采用Xtract计算各样本点对应的截面等效屈服曲率值Yj，并对等效屈服曲率Yj进行统计分析，得到其均值μ和标准差σ；将LHS计算得到等效屈服曲率的统计特征参数(μ和μ±2σ)与SVM-MCS法预测值的统计参数(μ和μ±2σ)对比，验证SVM-MCS法预测截面等效屈服曲率φy值的准确性，1-1截面和2-2截面的对比结果如图5和表2所示。此外，本文还采用各随机变量的均值计算得到不考虑高墩本身材料特性和截面尺寸等随机性的截面等效屈服曲率确定值(简称确定值)，与SVM-MCS法预测得到的各截面等效屈服曲率的均值进行了对比(见图6)，并按照式(2)计算分析了各随机变量对截面顺桥向和横桥向等效屈服曲率的贡献程度，如图7中所示。

由图5和表2可知，1-1截面和2-2截面的顺桥向和横桥向的等效屈服曲率均服从正态分布，采用SVM-MCS预测得到的等效屈服曲率的统计参数(μ和μ±2σ)与LHS计算得到截面等效屈服曲率的统计参数(μ和μ±2σ)最大误差仅为2.47%，因此采用SVM-MCS预测高墩截面的等效屈服曲率值可行，并具有较好的精确度。

由图6可知，高墩截面等效屈服曲率具有明显的离散性，并且顺桥向离散性较大、横桥向离散性较小；高墩Ⅰ号段截面的顺桥向等效屈服曲率均值与确定值差别较小，但是Ⅱ号段和Ⅲ号段差别较大，最大相差7.5%；横桥向等效屈服曲率均值与确定值在墩身Ⅱ号段中部截面有较大差距，最大差距为8.3%，墩身其他部分的截面等效屈服曲率均值与确定值相差较小。

由图7可知，各截面顺桥向和横桥向等效屈服曲率均对无约束混凝土峰值压应变的敏感性最低且敏感性系数值接近于零，但是由于高墩采用变截面形式，使得其他随机变量对截面顺桥向和横桥向等效屈服曲率的贡献程度沿墩高方向不断变化，其中：对于截面顺桥向等效屈服曲率，沿墩高方向各截面均对横截面高度和钢筋弹性模量敏感性较高，墩身Ⅱ号段和Ⅲ号段区域内部分截面的纵筋屈服强度敏感性系数较小而其他区域截面的纵筋屈服强度敏感性系数均最大，箍筋间距、混凝土容重、横截面宽度、纵筋截面面积和保护层厚度除在墩身Ⅱ号段和Ⅲ号段区域内部分截面的敏感性系数较大外，其他区域内截面的敏感性系数均较小；对于截面横桥向等效屈服曲率，沿墩高方向各截面均对横截面宽度和钢筋弹性模量敏感性较高，墩身Ⅱ号段中部区域截面的纵筋屈服强度敏感性系数较小而其他区域截面的纵筋屈服强度敏感性系数均最大，箍筋间距、混凝土容重、横截面高度、纵筋截面面积和保护层厚度除在墩身Ⅱ号段中部区域截面的敏感性系数较大外，其他区域内截面的敏感性系数均较小。

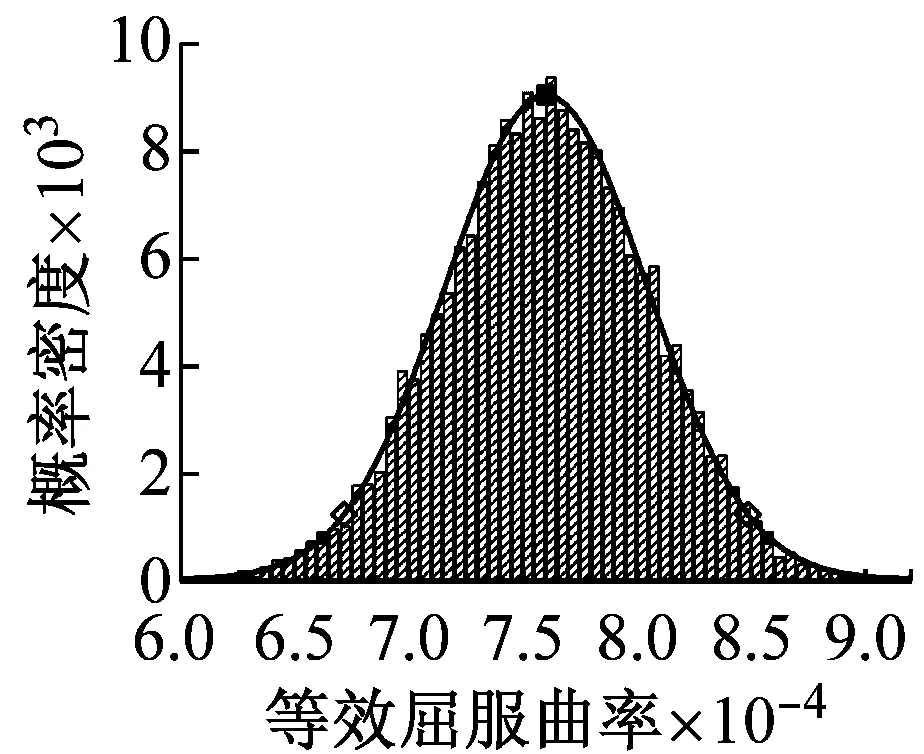
(a) 1-1截面顺桥向

(b) 1-1截面横桥向

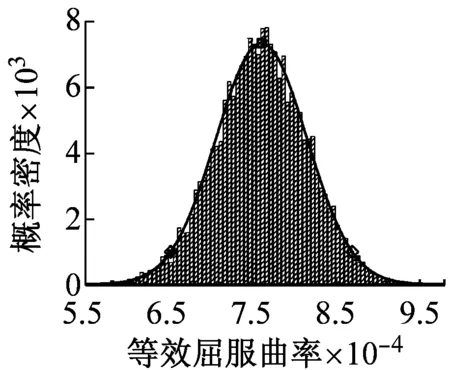
(c) 2-2截面顺桥向

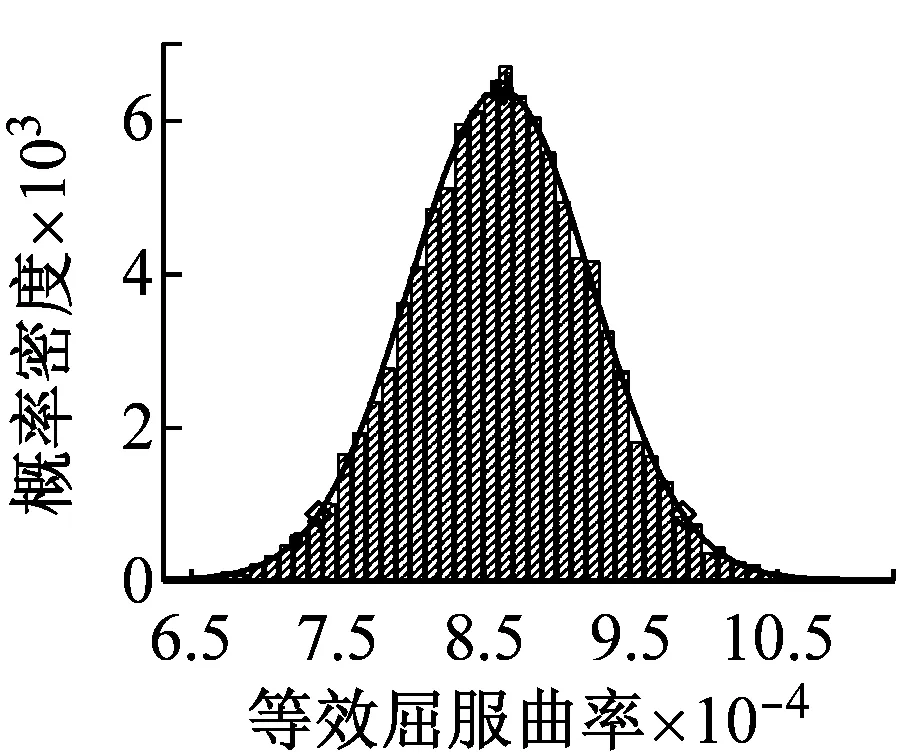
(d) 2-2截面横桥向

图5 等效屈服曲率概率分布图

Fig.5 Probability distribution graph of equivalent yield curvature

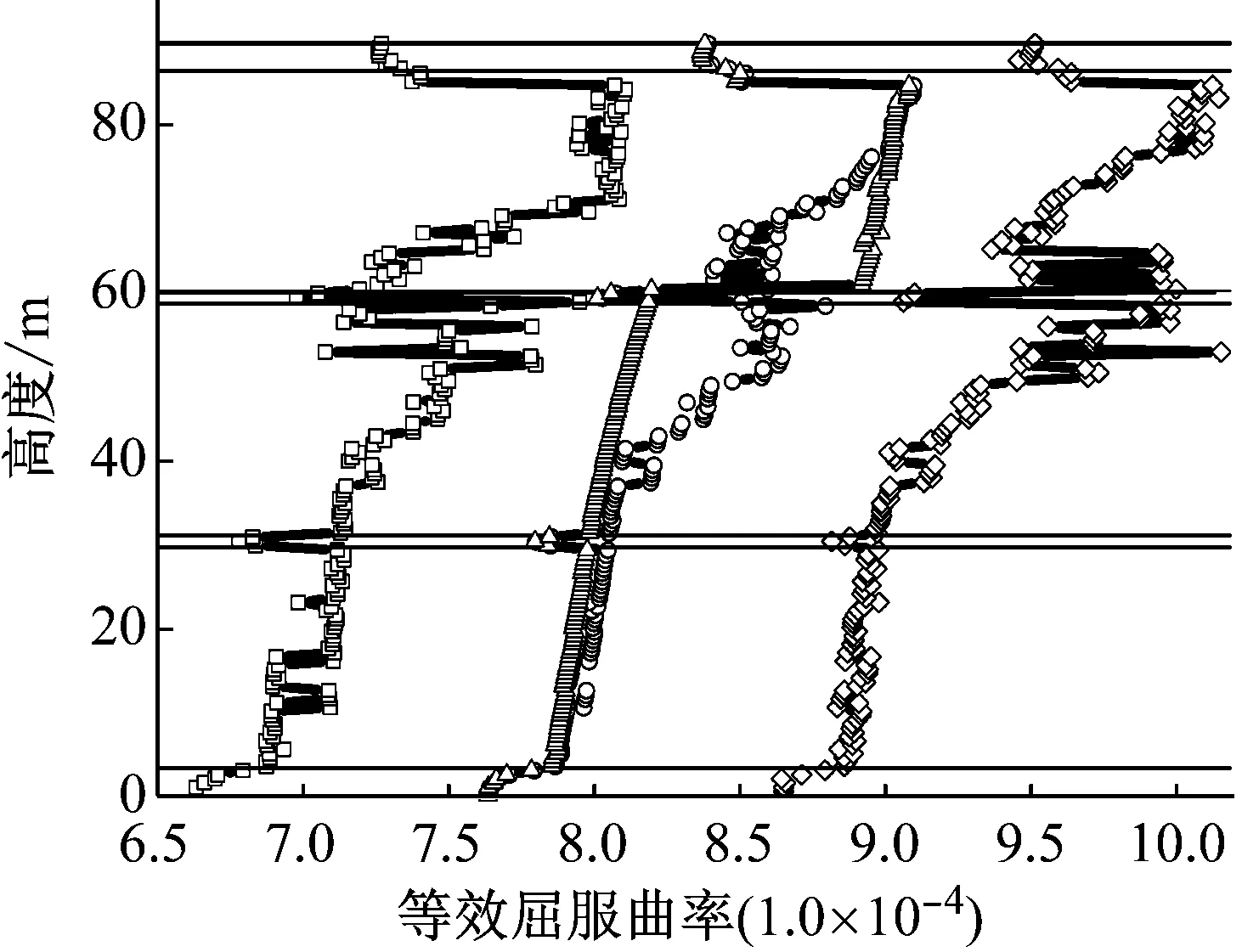
(a) 顺桥向

(b) 横桥向

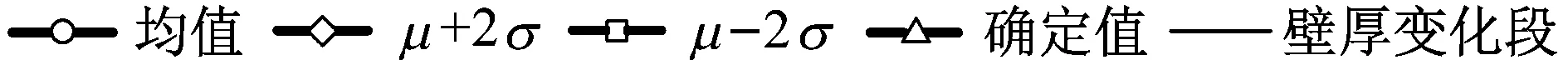
图6 等效屈服曲率对比图

Fig.6 Contrast diagram of equivalent yield curvature

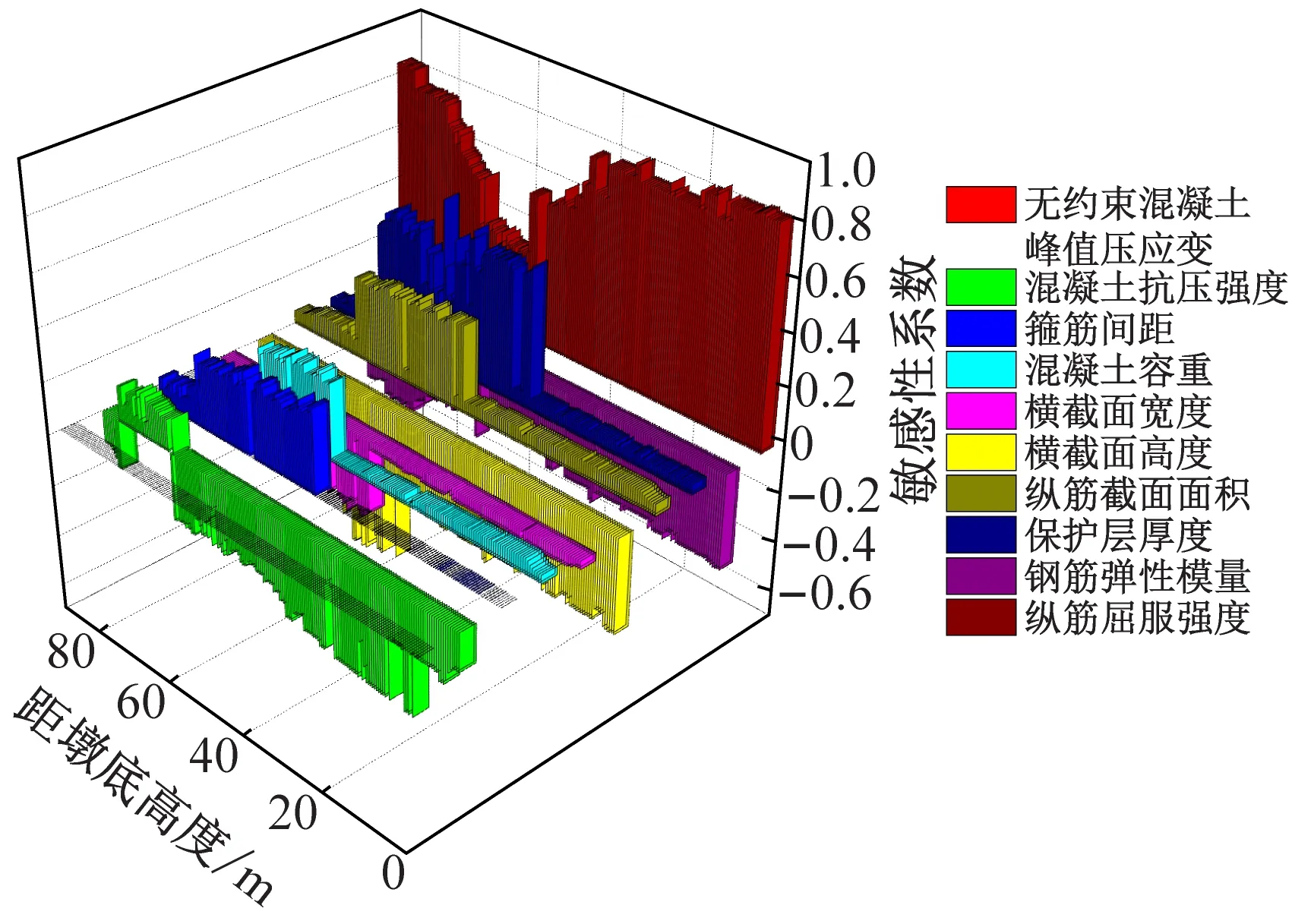
(a) 顺桥向

(b) 横桥向

由图6和图7对比可知，由于箍筋间距、混凝土容重、横截面宽度、横截面高度、纵筋截面面积、保护层厚度和纵筋屈服强度等随机变量对高墩横截面顺桥向和横桥向等效屈服曲率贡献程度沿墩高方向的不同变化规律，使得高墩截面等效屈服曲率顺桥向和横桥向离散性的不同，并且导致高墩Ⅱ号段和Ⅲ号段区域截面顺桥向等效屈服曲率、Ⅱ号段中部区域截面横桥向等效屈服曲率的均值和确定值之间有较大差距。因此，进行钢筋混凝土高墩塑性铰形成分析时，不能忽略等在给定地震动强度水平下，墩柱截面的塑性铰形成概率为

表2 等效屈服曲率统计特征参数值对比

4 基于JC法的塑性铰形成概率计算

Pf=P(S≥RIM=x)

(3)

式中：Pf为墩柱截面形成塑性铰的概率；S为地震动荷载作用下结构的动力响应，本文取截面曲率响应；R为结构抗力，本文取墩柱截面等效屈服曲率φy；IM为地震动强度参数；x为指定的地震动强度水平。

由式(3)可知，当墩柱截面的曲率响应S大于等效屈服曲率R时，墩柱截面开始形成塑性铰，但是由于桥梁结构参数和地震动等的不确定性，使得S和R均为随机变量，S和R的概率密度曲线如图8所示。

由图8可知，S和R的概率密度曲线重叠区域内，如果S≥R，则墩柱截面开始形成塑性铰。假定F(r,s)为(R,S)的联合分布函数，f(r,s)为(R,S)的联合概率密度函数，则墩柱截面塑性铰形成概率为

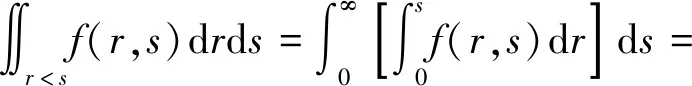
(4)

式中：fR(r)、fS(s)分别为墩柱截面等效屈服曲率概率密度函数和墩柱截面动力响应概率密度函数。

现有研究表明，同一强度地震荷载作用下，结构的动力响应S服从对数正态分布，同时“3.2”节中研究表明高墩截面等效屈曲曲率R服从正态分布，如果直接将S和R的概率密度函数方程代入式(4)中，难以直接积分解出截面塑性铰形成概率。因此，本文引入JC法将服从对数正态分布的截面动力响应S“当量正态化”为正态分布后，通过迭代计算得到截面可靠度指标β，并根据可靠度指标与失效概率之间的对应关系计算得到截面塑性铰形成概率Pf。

同一强度地震动荷载作用下截面动力响应S服从对数正态分布，其均值为mS、标准差为σS，则当量正态化为正态分布S′后的均值和标准差分别为mS′、σS′，根据JC法当量正态化原则，在设计验算点S*处，S与S′的分布函数值和概率密度值相等，如图9所示。即：

(5)

(6)

(7)

(8)

式中：VS为变异系数，VS=σS/mS。

可靠度指标β可采用截面曲率动力响应的当量正态分布S′与截面等效屈服曲率R计算

(9)

同时可以计算得到参数λR和λS′

(10)

(11)

则验算点R*和S*值为

R*=mR+βσRλR

(12)

S*=mS′+βσS′λS′

(13)

根据式(5)～式(13)，按如下步骤迭代计算得到钢筋混凝土高墩截面塑性铰形成概率：

步骤1假定“2.1”节中确定的各随机变量之间不具有相关性，采用拉丁超立方抽样方法对随机变量进行抽样，随机组合后得到50组随机变量数据，并按照第“1”节中的建模方法，采用OpenSees软件建立与随机变量数据对应的50个钢筋混凝土高墩有限元模型；

步骤2对“2.2”节中选取的50条近场地震波进行调幅处理，使之加速度峰值分别达到0.1g、0.2g、0.3g、0.4g、0.5g、0.6g、0.7g、0.8g、0.9g和1.0g，由此可得到50组共500条近场地震波样本；

步骤3将50个钢筋混凝土高墩有限元模型与调整后的50组近场地震波随机组合，分别按照顺桥向和横桥向地震动输入方向采用OpenSees进行IDA分析，记录墩身各截面的最大曲率响应值，并对同一地震动强度下的顺桥向和横桥向最大曲率值进行统计分析，得到顺桥向和横桥向曲率响应的均值mS和标准差σS；

步骤4采用“3.2”节中的SVM-MCS法预测高墩各截面顺桥向和横桥向的等效屈服曲率，并统计分析等效屈服曲率的均值mR和标准差σR；

步骤5假定初始验算点(R*,S*)，通常取R*=mR、S*=mS；

步骤6采用JC法，按照式(5)和式(6)对高墩截面曲率动力响应进行当量正态化处理，并按照式(7)和式(8)对计算当量正态分布的均值mS′和标准差σS′；

步骤7根据式(10)和式(11)计算参数λR和λS′；

步骤8利用式(9)计算截面可靠度指标β；

步骤9利用式(12)和式(13)计算新的验算点值R*和S*；

步骤10采用新的验算点值重复步骤6～9，直至∣上次β-本次β∣≤容许误差；

步骤11本次计算得到的β值即为截面可靠度指标，则截面塑性铰形成概率Pf=Φ(-β)；

步骤12绘制顺桥向和横桥向近场地震波作用下钢筋混凝土高墩截面塑性铰形成概率云图，并分析截面塑性铰形成规律。

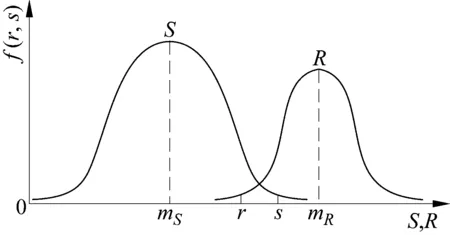
图8 S和R概率密度曲线Fig.8 Probability density curve of S and R

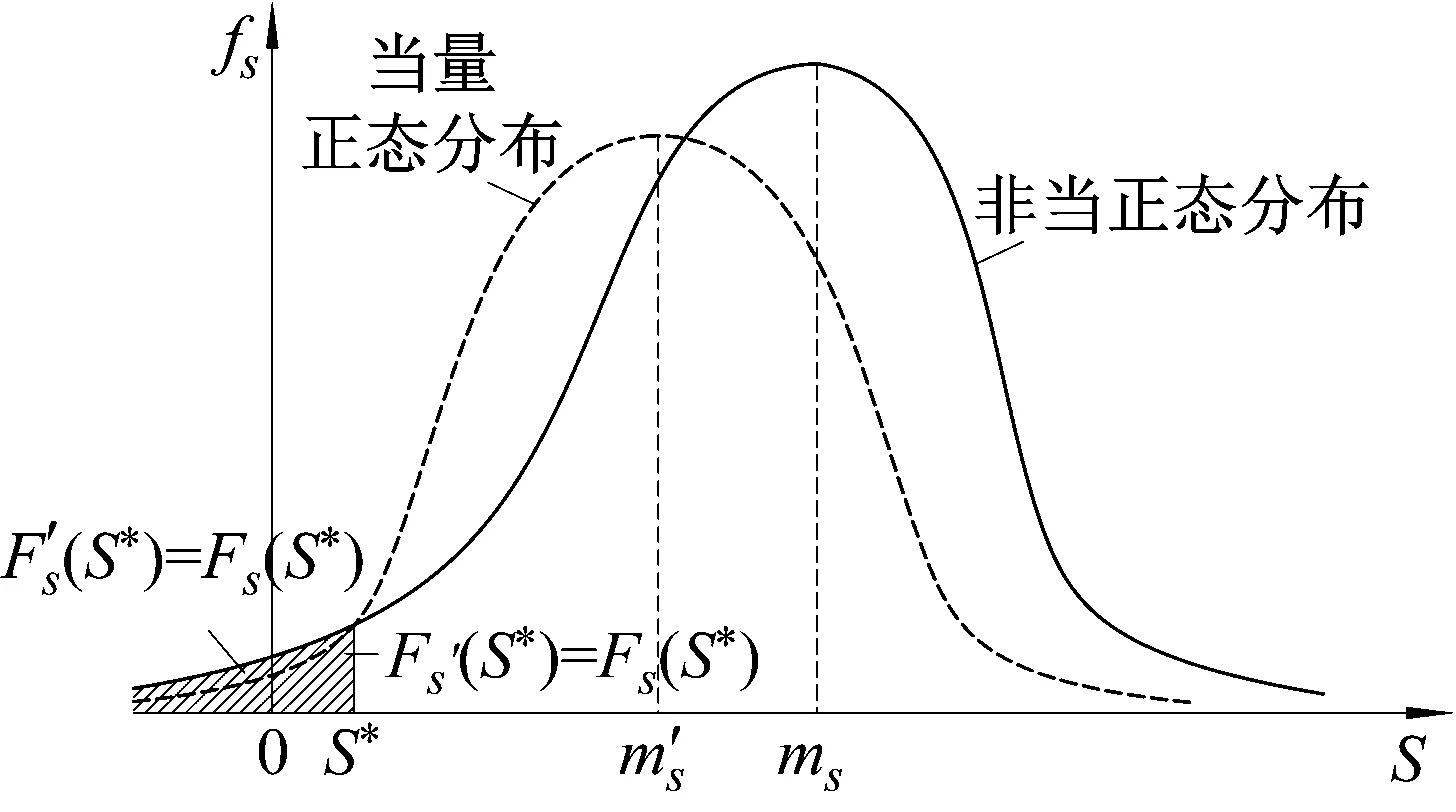
图9 当量正态化变换图Fig.9 Transformation graph of equivalent normalization

5 钢筋混凝土高墩塑性铰形成概率分析

塑性铰形成概率云图可以通过不同颜色表征沿墩身高度方向各个截面的塑性铰形成概率随近场地震强度的变化情况，具有简单、直观、易理解的优点，能很好地表征高墩截面塑性铰形成概率分布特征。根据第“4”节中的钢筋混凝土高墩截面塑性铰形成概率分析流程，对不同强度水平的顺桥向和横桥向近场地震动作用下高墩各截面的塑性铰形成概率进行分析，并绘制了塑性铰形成概率云图，如图10所示。

同时，本文还采用OpenSees软件按照表1中的各随机变量均值建立钢筋混凝土高墩有限元模型，并分别沿顺桥向和横桥向输入近场地震波进行IDA分析，将高墩各截面的最大曲率响应与截面等效屈服曲率φy的确定值对比，确定了只考虑近场地震动随机性时截面的塑性铰形成情况(简称塑性铰确定性结果)，并将形成塑性铰截面在图10中标记，以与本文提出的塑性铰形成概率分析方法进行对比研究。

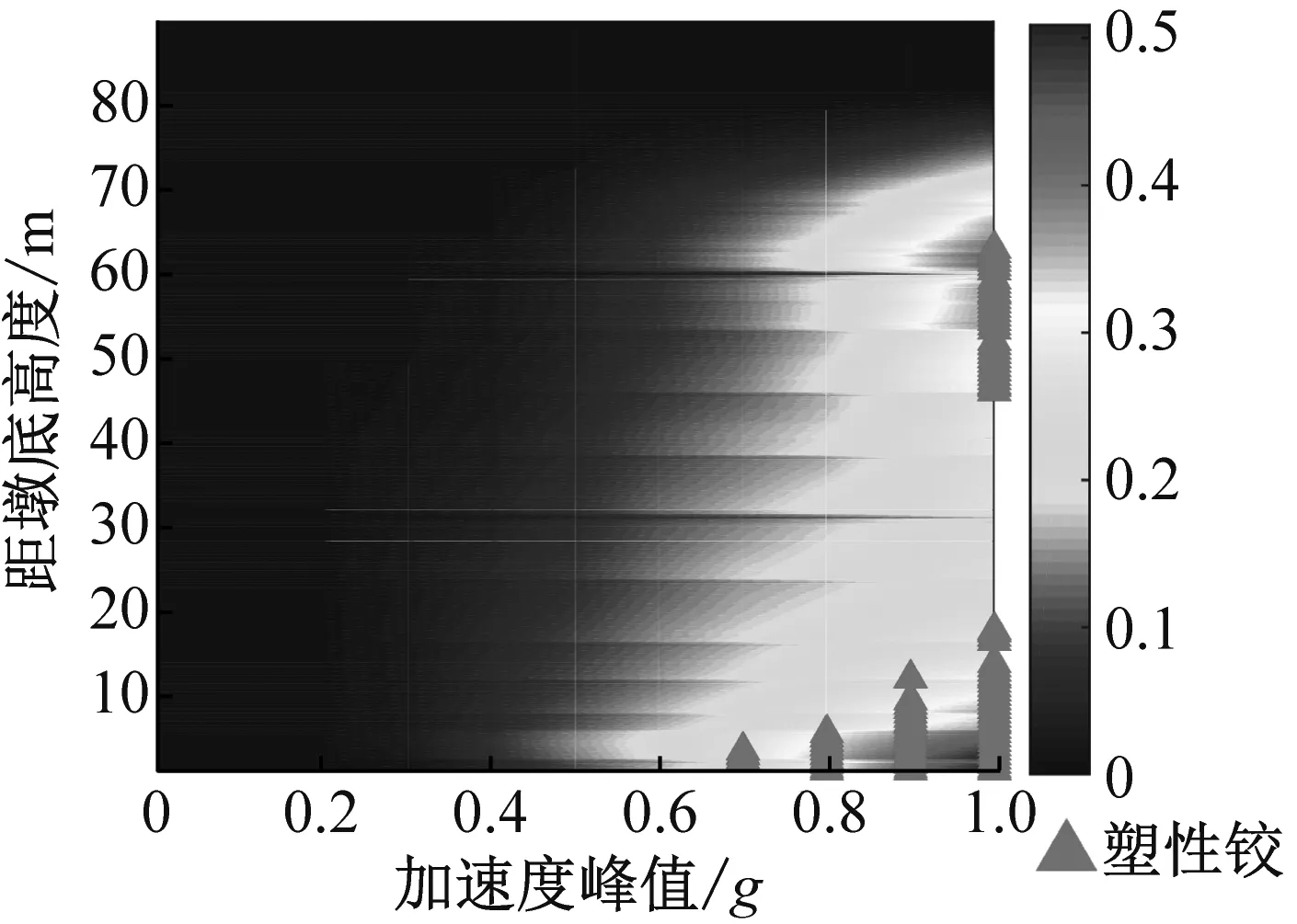
a) 顺桥向

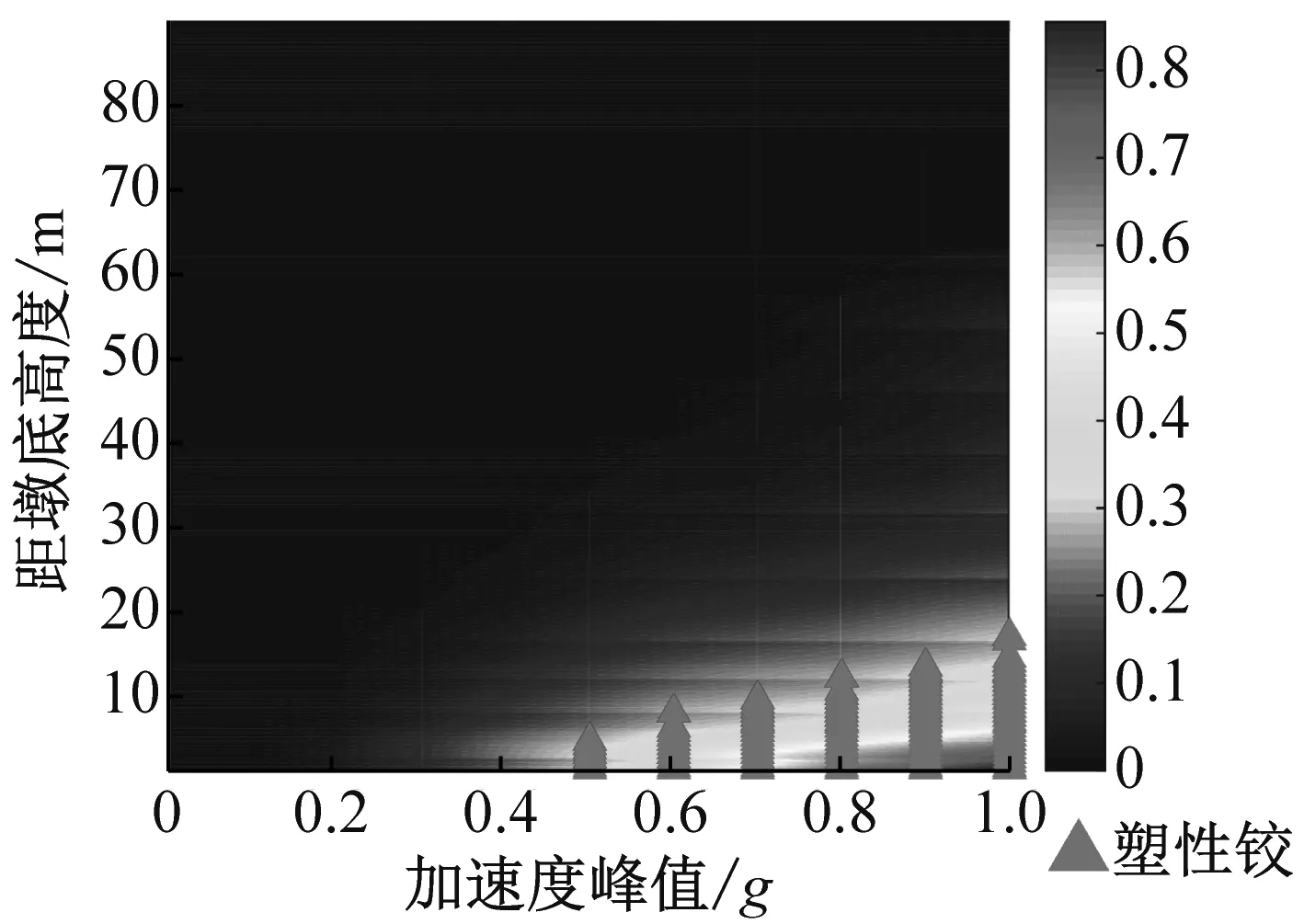
b) 横桥向

由图10可见，随着近场地震波加速度峰值的增加，钢筋混凝土高墩顺桥向和横桥向塑性铰形成概率不断增大，并且最大概率均出现在墩底区域，顺桥向为50.9%、横桥向为85.6%，但是顺桥向近场地震动作用下墩身中部塑性铰形成概率也较大，最大为42.5%，而横桥向墩身中部区域塑性铰形成概率均较小；只考虑地震波随机性时，当顺桥向地震波加速度峰值达到0.7g、横桥向地震波加速度峰值达到0.5g时，高墩底部区域开始形成塑性铰，并且随加速度峰值的增加，塑性铰形成区域的长度不断增加，当顺桥向近场地震波加速度峰值达到1.0g时，墩身中部开始形成塑性铰，塑性铰形成区域长度为17.2 m；将塑性铰形成概率与塑性铰确定性结果对比可知，当截面塑性铰形成概率达到26%时，高墩截面开始形成塑性铰，但是由于等效屈服曲率的离散性，使得顺桥向近场地震动作用下墩底和墩身中部塑性铰形成概率达到26%的区域长度均大于塑性铰确定性结果确定的区域长度，并且当顺桥向地震动强度达到0.9g时墩身中部便开始形成塑性铰，1.0g时墩身中部塑性铰区域长度为31.7 m，比塑性铰确定性结果确定的区域长度大84.3%；横桥向近场地震动作用下墩底塑性铰形成概率达到26%的区域长度与塑性铰确定性结果确定的塑性铰区域长度基本一致。因此，只考虑地震动随机性会低估顺桥向近场地震作用下钢筋混凝土高墩塑性铰形成区域的分布和长度。

6 结 论

通过对空心薄壁钢筋混凝土高墩工程实例进行顺桥向和横桥向近场地震动作用下塑性铰形成概率的分析研究，主要得到以下结论：

(1) 钢筋混凝土高墩各截面顺桥向和横桥向等效屈服曲率值具有明显的离散性且均服从正态分布，墩身Ⅱ号段和Ⅲ号段截面顺桥向等效屈服曲率均值与确定值差距较大，最大为7.5%，并且Ⅱ号段中部截面横桥向等效屈服曲率均值与确定值有较大差距，最大为8.3%，墩身其他部分的顺桥向和横桥向等效屈服曲率均值与确定值相差较小。

(2) 顺桥向和横桥向近场地震荷载作用下，钢筋混凝土高墩塑性铰形成概率的最大值均出现在墩底区域，顺桥向为50.9%、横桥向为85.6%，但是顺桥向近场地震动作用下，墩身中部区域塑性铰形成概率也较大为42.5%，而横桥向墩身中部区域塑性铰形成概率均较小。

(3) 根据截面塑性铰形成概率分析，顺桥向近场地震动作用下，墩身底部和中部区域均形成塑性铰区域，且长度大于只考虑地震波随机性的塑性铰确定性结果，墩身中部塑性铰区域长度达31.7 m，比塑性铰确定性结果大84.3%，横桥向近场地震动作用下，高墩仅墩底区域形成塑性铰且长度与确定性结果基本一致。

由于等效屈服曲率的随机性，使得只考虑地震动随机性会低估钢筋混凝土高墩的塑性铰分布和形成区域长度。因此，不应忽略等效屈服曲率等损伤判断指标的随机性，应综合考虑墩身参数和地震动的随机性对钢筋混凝土高墩抗震性能的影响。本文所得结论对采用单向放坡变截面的空心薄壁矩形钢筋混凝土高墩的简支梁桥进行抗震分析和加固维修时具有重要借鉴意义。