磁流变阻尼半主动隔振的钢弹簧浮置板轨道动力响应分析

韦凯 ，豆银玲 ，赵东锋 ，王平 ，杜香刚

(1. 西南交通大学 高速铁路线路工程教育部重点实验室，四川 成都，610031；2. 西南交通大学 土木工程学院，四川 成都，610031；3. 中国铁道科学研究院 高速铁路轨道技术国家重点实验室，北京，100081)

随着地铁建设规模的不断扩大，人们的出行满意程度不断提高。但是，随之带来的是不胜其扰的地铁振动与噪音。为了治理地铁振动与噪声，往往会在轨道上采取减振降噪措施。近年来，我国地铁领域主要采用高弹扣件、弹性轨枕与橡胶或钢弹簧浮置板轨道等减振轨道。在相同或可比的条件下，钢弹簧浮置板轨道的减振效果可达13.8 dB，是目前减振降噪效果最好的减振轨道[1]。在浮置板轨道减振性能及其工程应用方面，国内外开展了大量的相关研究。吴天行[2]在频域内建立了车辆−高弹扣件−弹性支承块或浮置板轨道的耦合系统模型，证明了该组合系统在中/高频具有更好的隔振效果。HUSSEIN等[3]提出了一种地铁隧道内不连续浮置板轨道的计算方法，结果表明不连续浮置板轨道会在远处显著增加其基频的振动响应。GUPTA等[4]提出了基于 Floquet变换的三维有限元−边界元耦合模型，并应用该模型计算分析了连续式和不连续式浮置板轨道的减振效果，结果表明浮置板轨道在低频段的减振效果比较差。刘维宁等[5]开展了钢弹簧浮置板轨道低频特征测试，实测数据表明：浮置板基频越低，减振效果越好，而且在基频附近振动放大也十分明显。鉴于浮置板轨道在基频附近有振动放大的现象，韦凯等[6]结合某地铁与建筑物合建工程，综合考虑合建结构与浮置板轨道的自振特征，提出了合建结构内浮置板轨道基频的设计原则。LEI等[7]结合有限单元法发展了车辆−钢弹簧浮置板轨道耦合动力学模型，并探讨了钢弹簧浮置板轨道关键设计参数的合理取值范围。根据已有的研究成果可知，浮置板轨道减振效果受限于它的固有频率。若想进一步提高浮置板轨道的减振效果，则需要降低浮置板支承刚度或增大浮置板质量。若增大质量则必增加建筑空间，同时增大工程投入；若降低刚度则会增加钢轨位移，但是为了保证车辆与轨道的安全服役，又不允许出现过大的钢轨与浮置板位移。按照CJJ/T 191—2012“浮置板轨道技术规范”[8]，浮置板轨道中的钢轨与浮置板的最大垂向振动位移分别不能大于4 mm和3 mm。显然，传统钢弹簧浮置板轨道的减振设计参数——质量与刚度的可调范围已经十分有限，因此，从阻尼角度优化浮置板轨道的低频减振效果值得尝试。近年来，随着磁流变阻尼半主动控制技术的快速发展，该项技术已普遍应用于土木工程结构抗震[9−11]。然而，与传统黏滞阻尼不同，磁流变阻尼属于库仑阻尼。大量研究表明：库仑阻尼必须与控制方法相结合，否则容易造成相反的控制效果[9−11]。为了将磁流变阻尼半主动控制技术应用于浮置板轨道中，本文作者将以钢弹簧浮置板轨道结构为基本形式，应用车辆−轨道耦合动力学理论[12]，并结合磁流变阻尼的力学特征与工作原理[13−15]，仿真分析地铁车辆−磁流变阻尼半主动隔振钢弹簧浮置板轨道垂向耦合系统的非线性振动响应特征，从轮轨安全性和轨道减振性2方面综合评价磁流变阻尼半主动隔振浮置板轨道的振动控制效果。

1 车辆−磁流变阻尼半主动隔振钢弹簧浮置板轨道垂向耦合动力学模型

为了探讨列车荷载作用下磁流变阻尼半主动隔振浮置板轨道的垂向振动特征，需要研究建立车辆−磁流变阻尼半主动隔振浮置板轨道垂向耦合动力学模型。

1.1 车辆模型

车辆模型采用两系悬挂的整车模型，该车辆模型共有10个自由度，能反映车体沉浮和点头运动、前后转向架的沉浮和点头运动以及4个轮对的垂向运动。采用我国额定负载的地铁A型车动参数进行数值仿真分析，具体取值见表1。

1.2 磁流变阻尼半主动隔振浮置板轨道模型

磁流变阻尼隔振钢弹簧浮置板轨道系统由钢轨、扣件、浮置板、钢弹簧、液体黏滞阻尼与磁流变阻尼组成。其中，钢轨采用 Euler梁模型，浮置板采用自由梁模型，扣件系统与钢弹簧+液态阻尼系统均采用Kelvin-Voigt模型，磁流变阻尼近似看作理想库仑摩擦力学模型(如图 1所示)；轮轨关系采用赫兹非线性弹性接触算法[12]。

在传统轨道板的自由梁模型[12]上，增加了磁流变阻尼的库仑干摩擦元件，因此，轨道板的自由梁垂向振动方程将变为(以向下为正)：

表1 地铁A型车的计算参数Table 1 Parameters of “Type A” subway vehicle

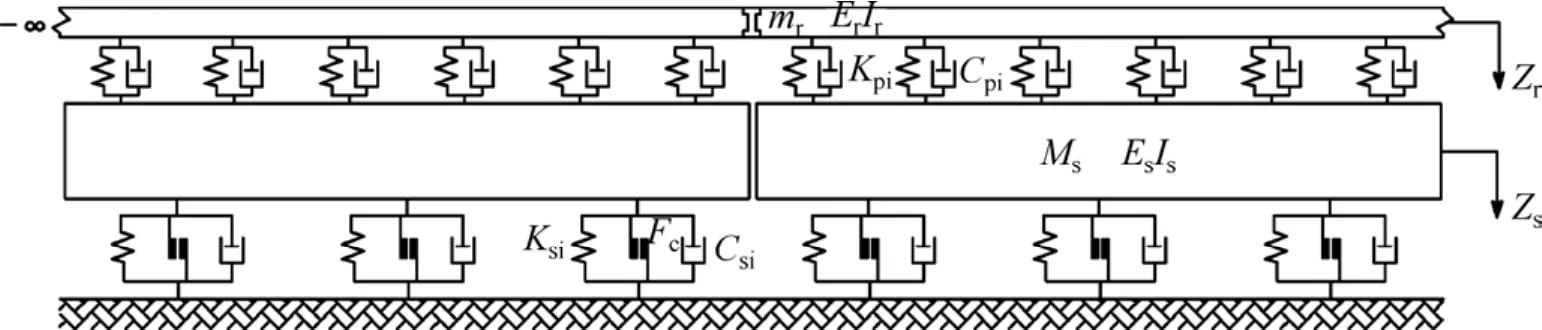
图1 磁流变阻尼隔振浮置板轨道的垂向动力学模型Fig. 1 Vertical coupled dynamic model of FST supported by steel spring, viscous damper and MR damper

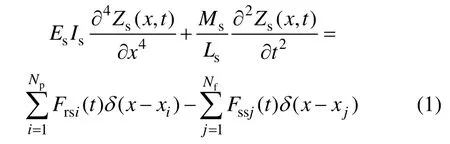
其中：

δ为Dirac函数；Es和Is分别为轨道板弹性模量、截面极惯性矩；Ms和Ls分别为轨道板质量、轨道板长度；Kpi和Cpi分别为第i个钢轨扣件刚度和黏滞阻尼系数；Zs(x,t)和分别为浮置板的垂向振动位移和速度；Frsi(t)为钢轨支点反力；Fssj(t)为第j个隔振器支点力；Np为1块板上钢轨扣件数量；Nf为1块板下隔振器数量；Ksj和Csj分别为第j个隔振器钢弹簧刚度、黏滞阻尼系数；Fc是常量的磁流变阻尼力；为符号函数，即当括号内振动速度是正数时，为 1；当括号内振动速度是负数时，为−1；当括号内振动速度是0时，也为0。

模型计算参数见表2。

1.3 磁流变阻尼半主动控制的数值模拟方法

磁流变阻尼的半主动控制策略可划分为 3类：1)经典的半主动控制算法，如天棚控制、地棚控制以及天地棚混合控制；2)线性反馈控制，如最优控制、鲁棒控制、滑模变结构控制等；3)智能控制，如模糊控制、神经网络控制、灰色理论及仿人智能控制等[13]。

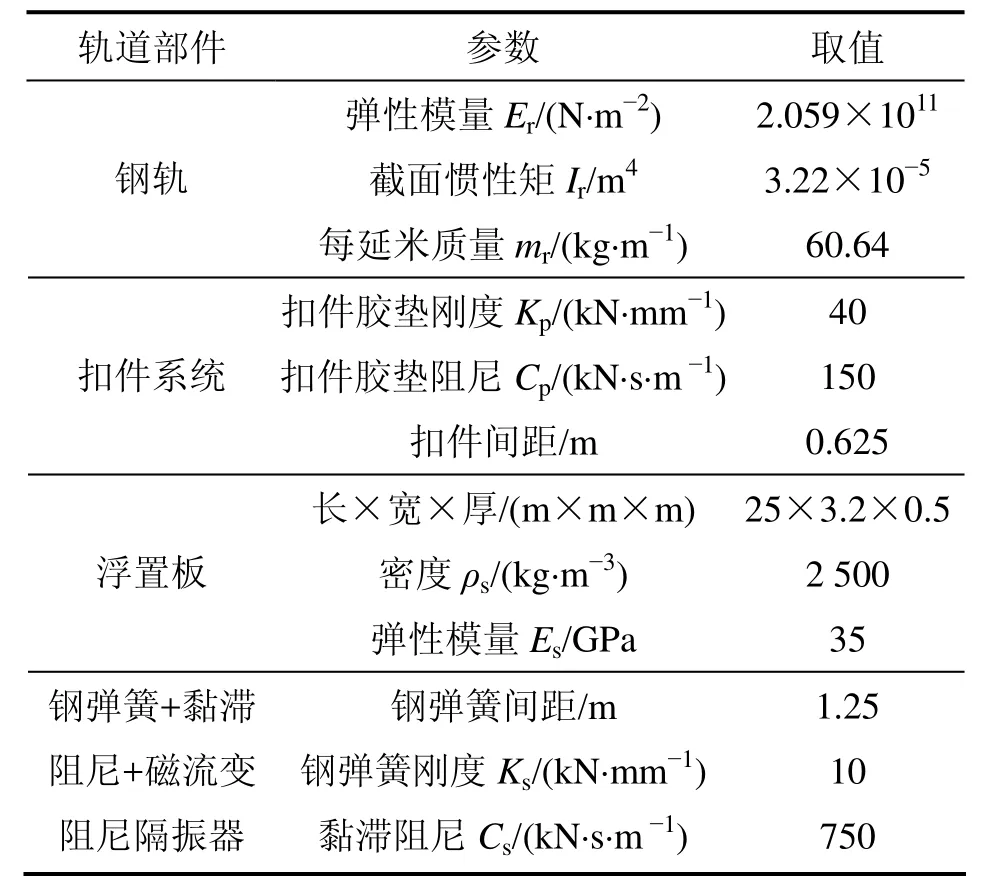
表2 轨道模型的参数Table 2 Parameters of track model

磁流变阻尼属于强非线性的阻尼材料，在已有的应用领域内，很难建立有效的控制算法以保证控制过程实时可控。因此，在非线性与随机性较强的轮轨耦合振动系统中，即使是最简单的控制策略都极具挑战。鉴于此，根据浮置板轨道以控制向下振动为主的特点，这里将采用简单实用的半主动控制策略(即半主动开−关(on−off)控制策略)，并结合浮置板振动速度拐点与磁流变阻尼响应滞后时间(一般在0.02~0.2 s[14])，设计了一种磁流变阻尼半主动开−关(on−off)控制的数值模拟方法，其示意图如图2所示。图中，Δt为时域积分步长；si和sj分别为ti和tj时刻的位移；sy为触发阀值；T为移动窗时间跨度。

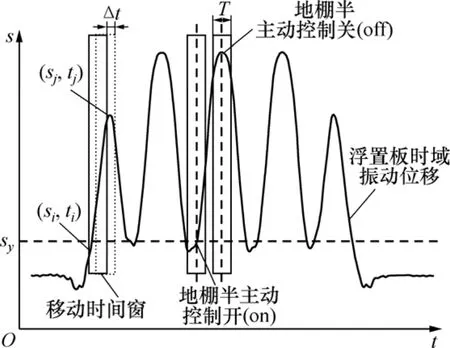
图2 浮置板轨道磁流变阻尼半主动开−关(on−off)控制的数值模拟示意图(以向下运动为正)Fig. 2 A numerical simulation method for on−off semi-active control strategy for MR dampers in FST model(downward displacement of floating slab is positive)

根据半主动开−关(on−off)控制策略，当浮置板由向上运动转为向下运动时(即浮置板最小垂向振动位移)，磁流变开始施加向上的阻尼力(即on状态)；当浮置板由向下运动转为向上运动时(即浮置板最大垂向振动位移)，磁流变阻尼开始停止工作(即off状态)。

由磁流变阻尼器的工作特点可知，当调整磁流变阻尼出力时，会产生明显的时滞现象[13−15]。为模拟这一现象，在数值计算中，设计了1个移动时间窗，时域积分步长取1×10−4s，移动窗与浮置板时域振动位移的交点分别为ti时刻的位移si和tj时刻的位移sj。模拟过程如下：当(ti+tj)/2时刻的位移大于触发阈值sy(在最小振动位移基础上，考虑一定的安全余量，本算例中sy取0.5 mm)时，通过判断tj时刻浮置板的振动方向(即(sj−si)/(tj−ti))来调整tj时刻磁流变阻尼力。通过移动时间窗的模拟可有效反映磁流变阻尼的响应滞后时间(即移动窗时间跨度的一半T/2，在本算例中取0.15 s)。

2 磁流变阻尼半主动隔振钢弹簧浮置板轨道的动力响应分析

2.1 计算工况

在本算例中，所模拟的运营条件是车速 60 km/h与美国5级高低不平顺谱(波长范围是0.1~30.0 m)。计算工况如表3所示。工况1是传统钢弹簧浮置板轨道工况(无磁流变阻尼)，工况 2~4是磁流变阻尼半主动隔振浮置板轨道工况。其中，工况1~3探讨应用半主动磁流变阻尼前后浮置板轨道的轮轨安全性与宽频减振效果，并确定浮置板轨道磁流变阻尼力的合理取值；工况2和4研究应用磁流变阻尼半主动隔振技术后浮置板轨道支承刚度的优化问题。

表3 计算工况Table 3 Calculation cases

2.2 磁流变阻尼半主动隔振对钢弹簧浮置板轨道动力响应的影响

通过试算发现，浮置板下磁流变阻尼力对车辆系统垂向振动响应的影响很小，因此，这里主要讨论 4个计算工况下钢轨垂向振动位移(加速度)、浮置板垂向振动位移(加速度)、轮重减载率与浮置板支点反力，用以量化评价浮置板轨道磁流变阻尼半主动隔振技术对轮轨安全性与轨道减振性的影响程度。

2.2.1 磁流变阻尼力对轮轨安全性的影响

在1~3工况下，钢轨、浮置板最大垂向振动位移与轮重减载率如图3和图4所示。

从图3可以看出：磁流变阻尼能显著降低钢轨与浮置板的最大垂向振动位移；当磁流变阻尼力由0增至 6 kN(12 kN)时，钢轨的最大垂向振动位移从3.97 mm 减小到 3.54 mm(2.99 mm)，减小比例达到10.8%(24.6%)，与此同时浮置板的最大垂向位移从3.11 mm 减小到 2.63 mm(2.11 mm)，减小比例达到15.4%(32.2%)。此外，应用磁流变阻尼后浮置板的最大垂向振动位移会发生一定的滞后，而且该滞后时间与仿真设计一致，均为0.15 s。

值得注意的是：磁流变阻尼力不宜过大，否则钢轨垂向位移容易出现上拱现象。从图3可知：在列车通过浮置板轨道的过程中，当磁流变阻尼力由0 kN增至 6 kN(12 kN)时，钢轨的最小垂向振动位移将从0.25 mm降至0.01 mm(−0.05 mm，向上运动为负)。因此，需要针对不同运营条件设计合理的磁流变阻尼力。在本算例中，考虑一定的安全余量，建议磁流变阻尼力取为6 kN。

另外，从图4可以看出：应用磁流变阻尼后地铁列车的轮重减载率基本不变，维持在0.45左右，这说明在本计算条件下磁流变阻尼不影响行车安全。

2.2.2 磁流变阻尼力对轨道减振性的影响

工况1~2的磁流变阻尼力对浮置板支反力时和频域响应的影响分别如图5和图6所示。

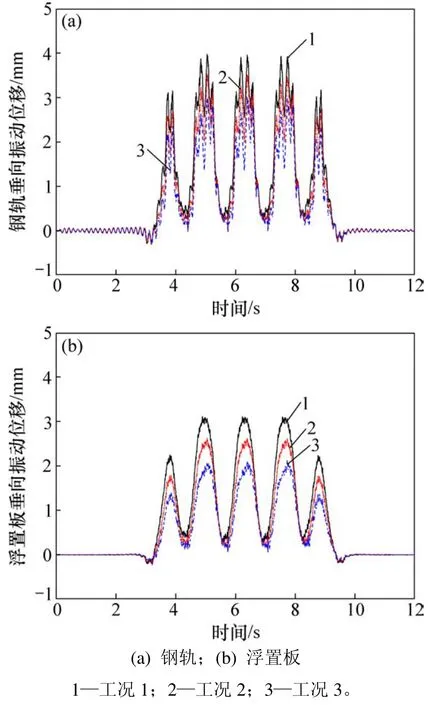
图3 工况1~3的浮置板轨道垂向振动位移时程曲线Fig. 3 Time-domain vertical vibration displacements of floating slab truck (FST)in Case 1, Case 2 and Case 3

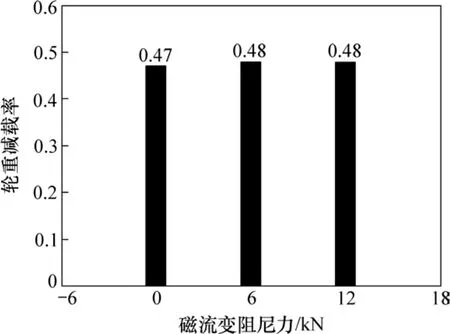
图4 磁流变阻尼力对轮重减载率的影响Fig. 4 Effect of magneto trheological damper force on reduction rate of wheel load

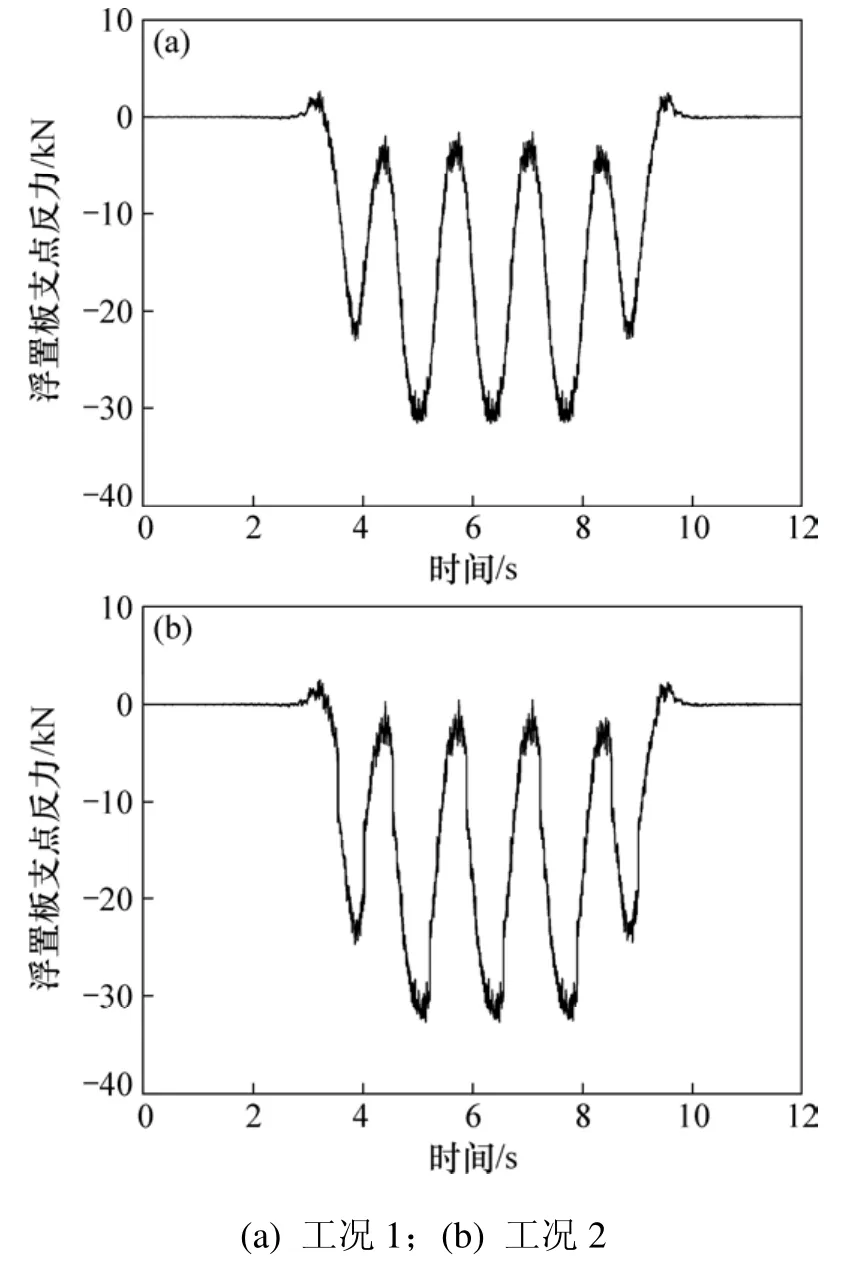
图5 工况1和工况2下浮置板支反力的时程曲线Fig. 5 Time-domain FST supporting forces in Case 1 and Case 2

图6 工况2的浮置板支反力分解时程曲线Fig. 6 Time-domain FST supporting forces in Case 2

从图5可知：工况1与2浮置板支反力的时程曲线的区别不大。但是，从图 6(a)可以看出：磁流变阻尼参振后，磁流变阻尼力是典型的方形波，其频率为0.7~1.0 Hz。磁流变阻尼参与浮置板振动的减振机理是：磁流变阻尼力在频率范围内重新分配了浮置板轨道向下传递的能量，不仅分担了浮置板轨道向下传递的振动能，而且以人体不敏感的极低频能量向周边扩散。因此，磁流变阻尼隔振浮置板轨道对环境振动的影响仅来自隔振器支反力(见图 6(b))，工况 2的隔振器支反力明显比应用磁流变阻尼前(工况 1)的低。

图7所示为工况1与工况2下隔振器支反力的1/3倍频有效值。

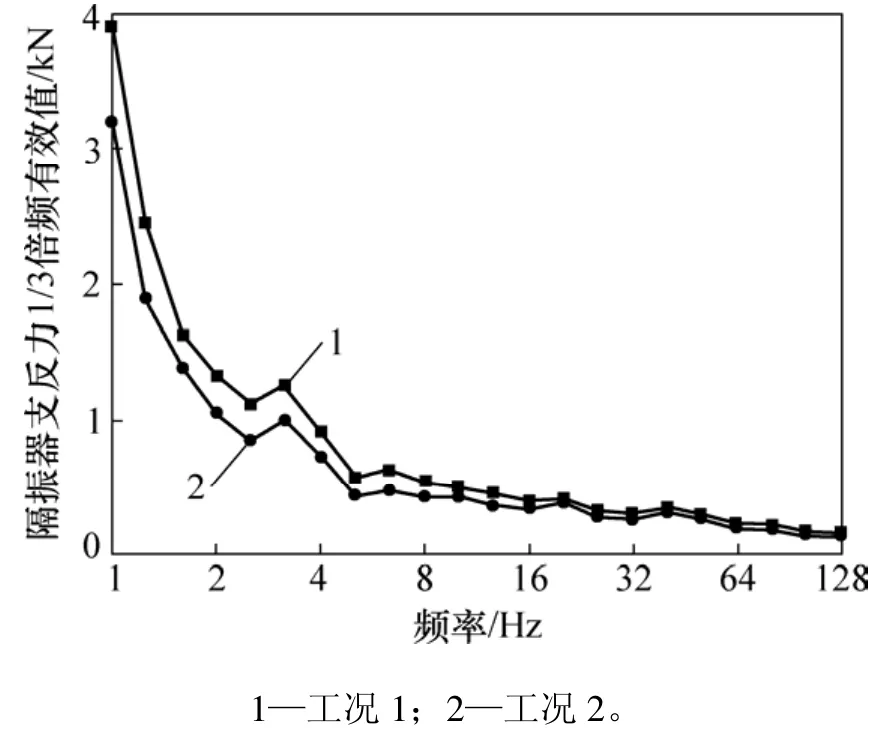
图7 工况1与2下隔振器支反力1/3倍频有效值Fig. 7 1/3 octave mean square roots (MSRs)of upporting forces supplied by vibration isolator in Case 1 and Case 2

从图7可以看出：磁流变阻尼主要提高钢弹簧浮置板轨道的低频隔振效率。与工况1相比，1/3倍频中心频率1.00，3.15与6.30 Hz的隔振器支反力有效值分别下降了18%，21%与24%。因此，将磁流变阻尼半主动隔振技术应用于浮置板轨道中是可行的，而且能够提升浮置板轨道低频减振效果。

2.2.2 浮置板轨道钢弹簧支承刚度的优化

由图3可知：磁流变阻尼能减小浮置板轨道的最大垂向振动位移。因此，浮置板支承刚度有进一步优化的空间。通过试算发现，在本算例中，浮置板支承刚度允许由10 kN/mm降至8 kN/mm，降幅可达20%。工况2和4的仿真计算结果表明，降低浮置板轨道支承刚度，会显著增大浮置板轨道的最大垂向振动位移，同时会进一步提高浮置板轨道的低频减振效率，见图8和图9。

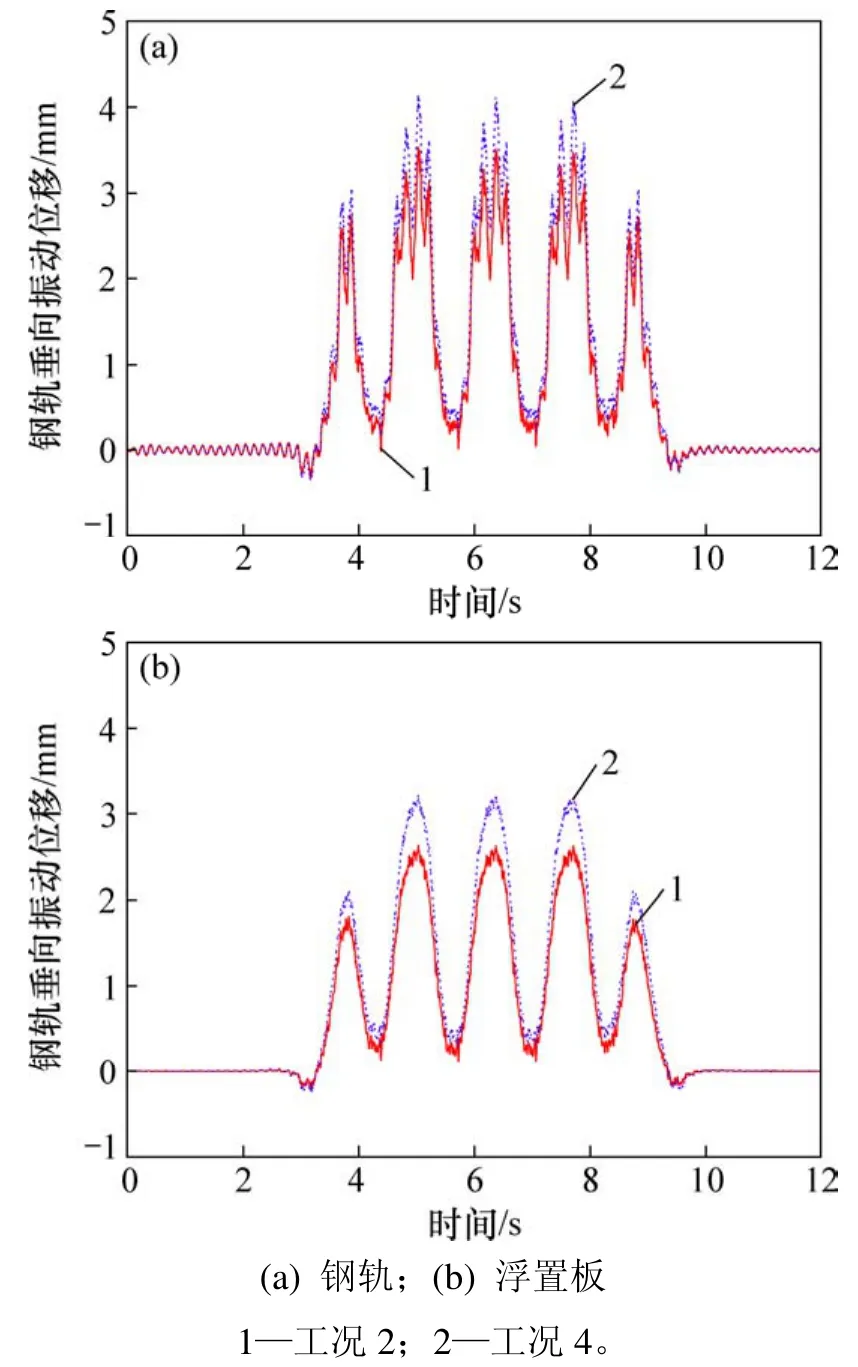
图8 工况2和工况4下浮置板轨道垂向振动位移时程曲线Fig. 8 Time-domain vertical vibration displacements of FST in Case 2 and Case 4

图9 工况2和工况4中隔振器支反力1/3倍频有效值Fig. 9 1/3 octave MSRs of supporting forces supplied by vibration isolator in Case 2 and Case 4

3 结论

1)磁流变阻尼半主动隔振的浮置板轨道能够显著降低轨道最大垂向振动位移，但对列车轮重减载率几乎没有影响。在磁流变阻尼力为 6 kN(12 kN)情况下，浮置板轨道的最大垂向位移减少 10.8%~15.4%(24.6%~32.2%)。因此，磁流变阻尼可以提高浮置板轨道最大垂向振动位移的安全余量。

2)在磁流变阻尼半主动隔振浮置板轨道体系中，过大的磁流变阻尼力易引起钢轨出现上拱现象(即过大磁流变阻尼力将导致钢轨的最小垂向振动位移通过平衡位置向上运动)，而过小的磁流变阻尼力又将无法达到良好的低频减振效果。因此，可借鉴或改进本文的研究思路，针对地铁不同运营条件，设计适宜的磁流变阻尼力。

3)磁流变阻尼半主动隔振技术能够重新调整浮置板轨道下部振动能量的频域分布，既能有效分担浮置板轨道下部1~16 Hz的低频振动能，也能将人体敏感频率(4~8 Hz)的振动能转变为极低频的振动能(＜1 Hz)向外传播。

4)在应用磁流变阻尼半主动隔振技术后，允许降低浮置板轨道支承刚度。此时，不但将显著提高浮置板轨道的最大垂向振动位移，而且会进一步提高浮置板轨道的低频减振效果。

[1]吴永芳. 轨道减振效果系统评价方法研究[J]. 中国铁道科学,2013, 34(3): 1−6.WU Yongfang. Investigation into the evaluation method for vibration damping effect of track system[J]. China Railway Science, 2013, 34(3): 1−6.

[2]吴天行. 轨道减振器与弹性支承块或浮置板轨道组合的隔振性能分析[J]. 振动工程学报, 2007, 20(5): 489−493.WU Tianxing. On effectiveness of vibration isolation for super-elastic rail support combined with booted sleeper or floating slab track[J]. Journal of Vibration Engineering, 2007,20(5): 489−493.

[3]HUSSEIN M F M, HUNT H E M. A numerical model for calculating vibration due to a harmonic moving load on a floating-slab track with discontinuous slabs in an underground railway tunnel[J]. Journal of Sound and Vibration, 2009,321(1/2): 363−374.

[4]GUPTA S, DEGRANDE G. Modelling of continuous and discontinuous floating slab tracks in a tunnel using a periodic approach[J]. Journal of Sound and Vibration, 2010, 329(8):1101−1125.

[5]刘维宁, 丁德云, 李克飞, 等. 钢弹簧浮置板轨道低频特征试验研究[J]. 土木工程学报, 2011, 44(8): 118−125.LIU Weining, DING Deyun, LI Kefei, et al. Experimental study of the low-frequency vibration characteristics of steel spring floating slab track[J]. China Civil Engineering Journal, 2011,44(8): 118−125.

[6]韦凯, 周顺华, 翟婉明, 等. 地铁与建筑物合建中不同固有频率钢弹簧浮置板轨道的适用性分析[J]. 土木工程学报, 2011,44(11): 134−142.WEI Kai, ZHOU Shunhua, ZHAI Wanming, et al. Applicability of steel-spring floating-slab tracks of different natural frequencies for integrated metro-and-building structures[J].China Civil Engineering Journal, 2011, 44(11): 134−142.

[7]LEI Xiaoyan, JIANG Chongda. Analysis of vibration reduction effect of steel spring floating slab track with finite elements[J].Journal of Vibration and Control, 2014, 22(6): 1462−1471.

[8]CJJ/T 191—2012, 浮置板轨道技术规范[S].CJJ/T 191—2012, Technical code for floating slab track[S].

[9]HEO G, KIM C, LEE C. Experimental test of asymmetrical cable-stayed bridges using MR-damper for vibration control[J].Soil Dynamics and Earthquake Engineering, 2014, 57: 78−85.

[10]UZ M E, HADI M N S. Optimal design of semi-active control for adjacent buildings connected by MR damper based on integrated fuzzy logic and multi-objective genetic algorithm[J].Engineering Structures, 2014, 69(9): 135−148.

[11]NICOLA C. Semi-active control of a wind turbine via magneto-rheological dampers[J]. Journal of Sound and Vibration,2015, 345: 1−17.

[12]翟婉明. 车辆−轨道耦合动力学[M]. 4版. 北京: 科学出版社,2015: 38−41.ZHAI Wanming. Vehicle-track coupled dynamics[M]. 4th ed.Beijing: Science Press, 2015: 38−41.

[13]李忠献, 徐龙河. 新型磁流变阻尼器及半主动控制设计理论[M]. 北京: 科学出版社, 2012: 9−10.LI Zhongxian, XU Longhe. A new type of magnetorheological damper and semi-active control theory[M]. Beijing: Science Press, 2012: 9−10.

[14]周云, 谭平. 磁流变阻尼控制理论与技术[M]. 北京: 科学出版社, 2007: 267−268.ZHOU Yun, TAN Ping. Control theory and technology of Magnetorheological damper[M]. Beijing: Science Press, 2007:267−268.

[15]ZHOU Q, NIELSEN S R K, QU W L. Semi-active control of three-dimensional vibrations of an inclined sag cable with magneto-rheological dampers[J]. Journal of Sound and Vibration,2006, 296(1/2): 1−22.