爆炸分离钛合金板的研究

胡坤伦， 汪 齐， 王 猛， 曹 杰， 韩体飞

(安徽理工大学 化学工程学院，安徽 淮南 232001)

航空发动机非包容事故会导致机毁人亡的严重空难。高速高能的危险碎片穿透机匣飞出，会击伤飞机的机舱、油箱、液压管路和电器控制线路等，严重危及飞行安全，因此进行航空发动机机匣包容性研究具有重要意义。机匣包容试验是验证机匣对折断后飞出的转子叶片包容能力的试验[1]，在进行机匣包容试验时要求钛合金飞轮叶片在特定位置和转速下断裂，且无过多的剩余速度和破片飞溅。现决定用爆炸的方法达到叶片分离且不给叶片提供多余动力的目的，叶片打孔处剖视图如图1所示。目前，对爆炸分离的研究主要在航天工程领域的火工分离装置以及涡轮发动机的转子叶片上。丁继锋等[2]多方面调研了目前国内外该领域在火工冲击、模拟试验以及降低损害等方面的进展，指明了国内之后在该领域的重点工作进展；武新峰等[3]基于ANSYS/LS-DYNA软件设计了一种卫星火箭连接结构的计算方式，并通过实验结果验证了包带的相关参数会对星箭分离过程产生巨大影响；黄含军等[4-5]对爆炸分离冲击环境地面模拟试验进行了研究，对今后的发展趋势进行了预测。Takeuchi等[6]利用简单圆柱壳体建立模型，对航天器的分离断裂过程进行模拟，对冲击响应做出了判断。Troshehenko等[7]研究了压气机转子叶片钛合金的疲劳裂纹扩展，确定了试验中试件的应力强度因子的方法，综合研究了叶片和叶片材料疲劳裂纹扩展。Warren等[8]研究了各向同性线性金属块在受到准静态拉伸应力后的应力状态和断裂过程。

爆炸场影响合金板断裂的因素非常复杂，若采用全面实验法，考虑装药量、装药密度、炸药种类、板材种类、板材壁厚、缓冲材料、缓冲层厚度等7个影响因子(以上并未考虑装药结构)，按每影响因子5水平，需要进行78 125 (57)次试验[9]，要完成如此庞大的试验量在实际操作中几乎不可能。试验中，若装药量过少，则合金叶片未完全断裂，达不到分离效果；装药量过多，则在合金叶片分离后提供使其加速的多余动力，并产生爆炸破片，也达不到所需要求。为达到恰好分离叶片的目的，合适的装药量及装药结构的选择尤为重要。

本文基于量纲分析的相似性研究，以得到合金板断裂问题依赖的主要无量纲自变量[10-11]。在量纲分析的基础上，利用AUTODYN中的SPH(Smoothed Particle Hydrodynamics)法对板材断裂过程进行数值模拟[12]，通过逐渐改变参数值，使板块恰好分离，为爆炸分离钛合金板试验预估出出药量。参考量纲分析、数值模拟结果进行爆炸试验，通过不耦合(添加一定厚度的缓冲材料)和间隔(添加一定长度的导爆管)装药结构调整药量，以最终确定恰使钛合金板的分离的药量。飞轮叶片打孔处局部剖视图,如图1所示。

图1 飞轮叶片打孔处局部剖视图

1 量纲分析

利用量纲分析法对爆炸切断问题进行分析,得到决定爆炸过程中板材断裂的主要控制参数：① 炸药参数：装药量Q(可由孔径φ换算)、装药密度ρe、单位质量炸药的化学能Ee、爆炸产物膨胀指数γe、装药长度l，线装药密度ql；② 钛合金板材参数：最小壁厚d、密度ρ、弹性常数E、泊松比μ、破坏强度S；③ 缓冲层参数：厚度δ、密度ρb、状态方程压力参数Bb、绝热指数γb。

耦合装药时要将板材分离而不产生爆炸破片，此时的判定条件是速度v=0，可写出关系式为

v=f(ql,ρe,Ee,γe;ρ,E,μ,S,d)

(1)

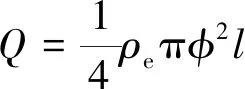
(2)

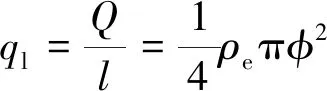
(3)

选取ρe,Ee,d作为基本量，可得到无量纲函数关系

(4)

如果模型试验采用与原型相同种类的炸药和目标介质，式(4)可以简化为

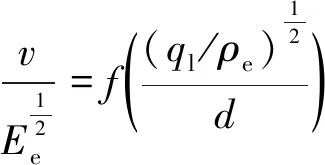
(5)

将式(3)代入式(5)可得：

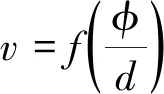
(6)

不耦合装药时要将板材分离而不产生爆炸破片，此时的判定条件仍是速度v=0，可写出关系式为

v=f(ql,ρe,Ee,γe;ρ,E,μ,S,d;ρb,Bb,γb,δ)

(7)

选取ρe,Ee,d作为基本量，得到无量纲函数关系

(8)

如果模型试验采用与原型试验相同种类的炸药和目标介质，式(8)可以简化为

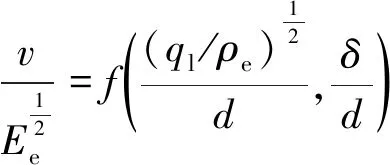
(9)

最后可得

(10)

分析可知，在模型试验采用与原型试验相同种类的炸药和目标介质的前提下，耦合装药和不耦合装药也符合几何相似律[13]，且板材最小壁厚d、装药直径φ和缓冲层厚度δ之间有一确定最佳比例关系。若要分离合金板板，需通过实验寻找这一最佳比例。

2 数值模拟

2.1 计算模型

为进一步缩小目标范围以减少试验量，利用AUTODYN的SPH方法对合金板爆炸分离进行了数值模拟，预估出恰好使合金板分离的药量，为进行爆炸切断实验提供参考。模型尺寸为：120 mm×66 mm×12 mm，板材侧面中心位置沿长度方向有孔径为r、长度为120 mm的装药孔。板材采用Puff状态方程、Von-Mises强度模型和Hydro失效模型，炸药采用JWL状态方程，钛合金材料参数及黑索今炸药材料参数见表1、表2。计算过程中通过改变装药孔孔径来改变装药量，在所建模型中起爆方式设为中心点(POINT)起爆，为节省计算时间采用1/2平面对称模型建模[14-15]，模拟模型如图2所示。钛合金板模型中在约束最薄弱的方向上(Y轴方向)设置了监测点1，通过观测监测点的速度来判断合金板切断过程中的运动状态。

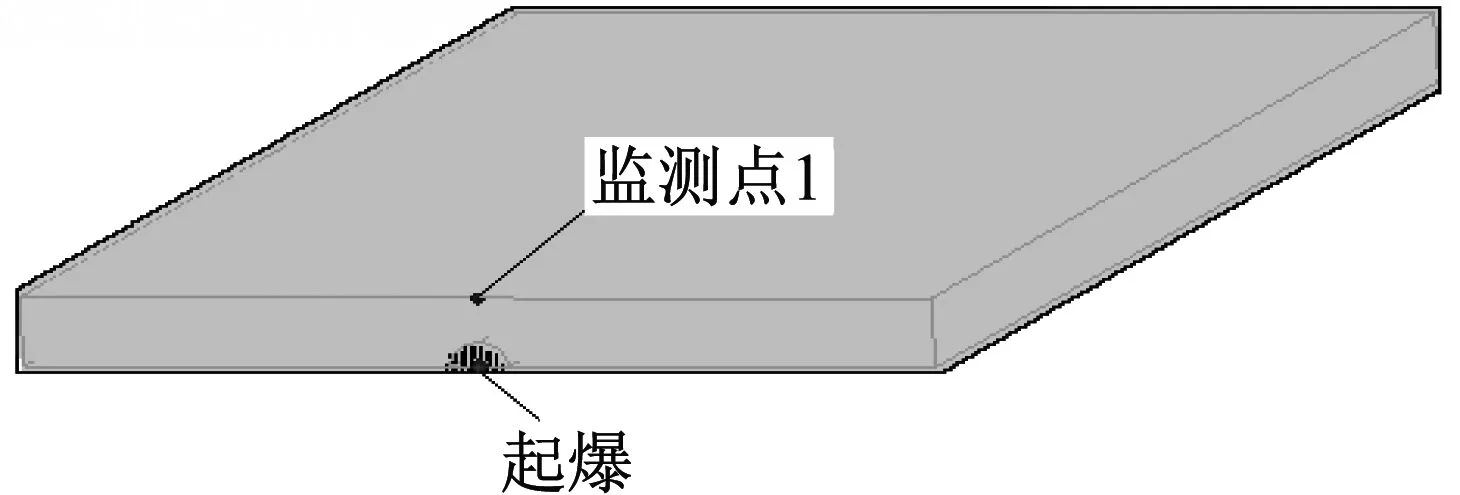
图2 钛合金板数值模拟模型

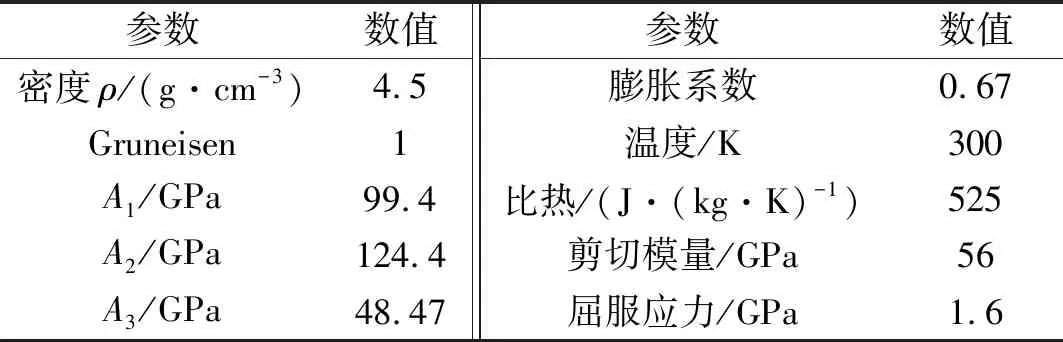
表1 钛合金材料Puff状态方程参数

表2 黑索今炸药JWL状态方程参数

2.2 计算结果与分析

通过不断调整模型的装药直径进行模拟试验：当药量过量时则减小装药直径，当药量不足时则增大装药直径。先从较大装药直径时开始模拟，然后通过二分法缩小范围，当缩小到一定范围后，再以0.1 mm步长进行升降试探计算。最终当装药孔径为4.7 mm并全装药时，钛合金板监测点1的速度最终趋于零而正好不会飞溅，通过计算得此时炸药量为2.081 g。图3为爆炸后的状态。图4为监测点的速度变化曲线。

(a) 合金板完全断裂

(b) 合金板趋近于恰好分离

当药量大于2.081 g时，合金板完全断裂，产生大量破片，如图3(a)所示。监测点的速度变化曲线，如图4(a)所示。炸药爆轰结束瞬间，合金板被冲击压缩，监测点1速度瞬间增大至220 m/s，当冲击波传播到合金板的自由表面后，反射一稀疏波，合金板继续膨胀，监测点1速度迅速增大至280 m/s。由于附近物质质点的约束，监测点速度下降至200 m/s，此时又在高温高压爆生气体的膨胀下，监测点1的速度再次增长，但是爆生气体的膨胀相对于冲击波的传播是一个相对缓慢的过程，因此速度增长相对缓慢。当药量为2.081 g时，合金板并未分离，仅板两侧并略微鼓起并出现裂纹，如图3(b)所示。从图4(b)可知，监测点1的速度瞬间达到最大值，随后速度值一直上下波动且幅值逐渐减小，最后逐渐趋近于零，监测点1并未飞出。此过程可以将监测点1看作薄层飞片上的一点，“飞片”在前后反射稀疏波和压缩波的相互作用下不断跳跃式变化[16-17]，因波在传播过程中不断衰减，与此同时，受附近的物质质点的约束作用，故而速度在零点附近震荡，直至衰减为零。

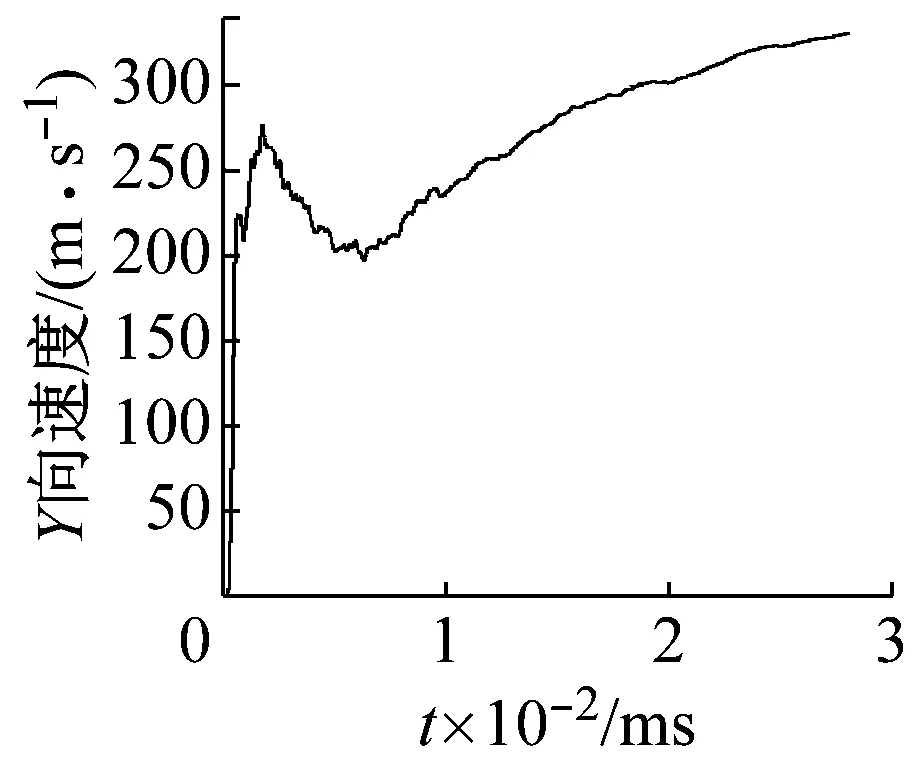
(a) 合金板完全断裂

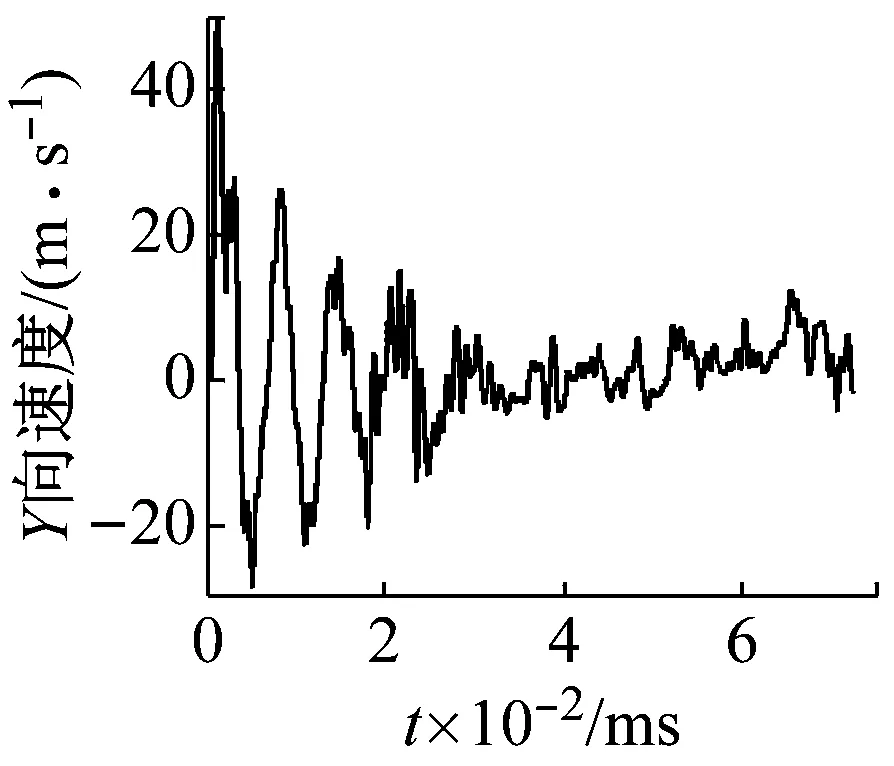
(b) 合金板趋近于恰好分离

3 钛合金板分离试验

3.1 试验设计

采用悬挂方式，从装药量为2.002 g开始，逐步调整装药结构改变装药量，至合金板恰好分离。因几何相似律的存在，以及通过不断改变板材孔径的大小来改变装药量的操作不便，试验中固定板材厚度为12 mm，孔径为8 mm，此时即固定合金板的最小壁厚为2 mm。板材尺寸为：120 mm×66 mm×12 mm。通过两种方法减少炸药量：一是在合金板孔内添加厚度为δ的缓冲材料创造不耦合装药条件(装药直径小于8 mm)，加入一定厚度的缓冲材料可以减小装药直径以降低药量，同时也可让爆炸能量达到缓释的效果，减小爆炸对合金板的局部破坏。当装药直径减小到小于黑索今的爆轰临界直径时，黑索今将无法爆轰，因此不能一直减小装药直径，可用塑料套管包裹导爆管，然后取所需的间隔长度，创造间隔装药条件以减少药量。

3.2 试验结果及分析

如表3所示,表中Ci(i=1,2,3,4,5)表示从起爆端开始第i段的长度(单位：mm)。当i为奇数时，该段为装药长度，即图5中的阴影部分长度；当i为偶数时，该段为间隔长度，即图5中的空白部分长度。

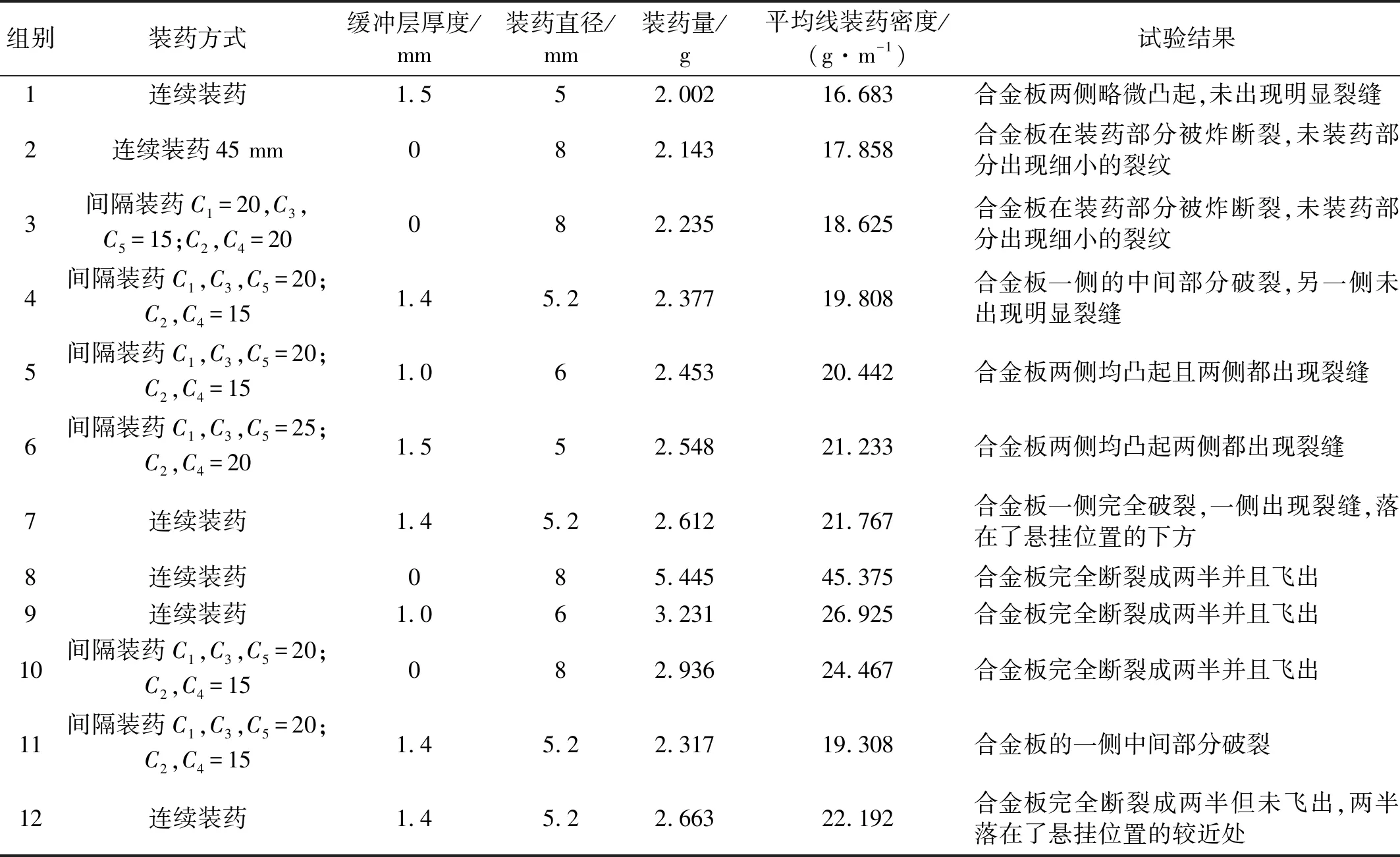
表3 试验结果

图5 装药结构示意图

由表3可知，当试验药量小于2.612 g时，无法达到分离合金板的目的。当药量为2.612 g时，达到了较为理想的结果，爆炸效果如图6所示。合金版的一面完全断裂，另一面鼓起并出现裂缝，板块落在了悬挂位置的下方。当药量继续增大时，又进行了3组试验对比，发现药量大于2.612 g会炸飞板块，因此设计了第11组试验进行对比，第11组药量为2.317 g，此时无法达到分离板块的效果。所以进行了第12组试验，药量为2.663 g，爆炸效果如图7所示。板块完全分离但没有飞出，两半落在了悬挂位置的较近处，分离效果较为理想。试验用炸药量变化曲线如图8所示。

图6 第7组试验效果图

图7 第12组试验效果图

通过以上12组试验，可发现第7组和第12组的试验效果较好，此时药量分别为2.612 g、2.663 g，其中第7组试验效果最佳。

试验中存在着一些因素会给试验带来一定的误差，如：板材切割和打孔过程中存在的尺寸误差(打孔偏离中心位置，造成孔两侧最小抵抗线不等)，容易出现如第7组试验的单边断裂现象。试验中装药线密度无法精确控制，使得爆炸切断出现不均匀误差。起爆端装药未成长为理想爆轰也对试验造成影响，使沿轴线呈现不均匀破裂。此外，当装药尺寸接近临界直径时，爆炸能量释放和对目标介质作用是否符合几何相似律，还有待进一步研究。

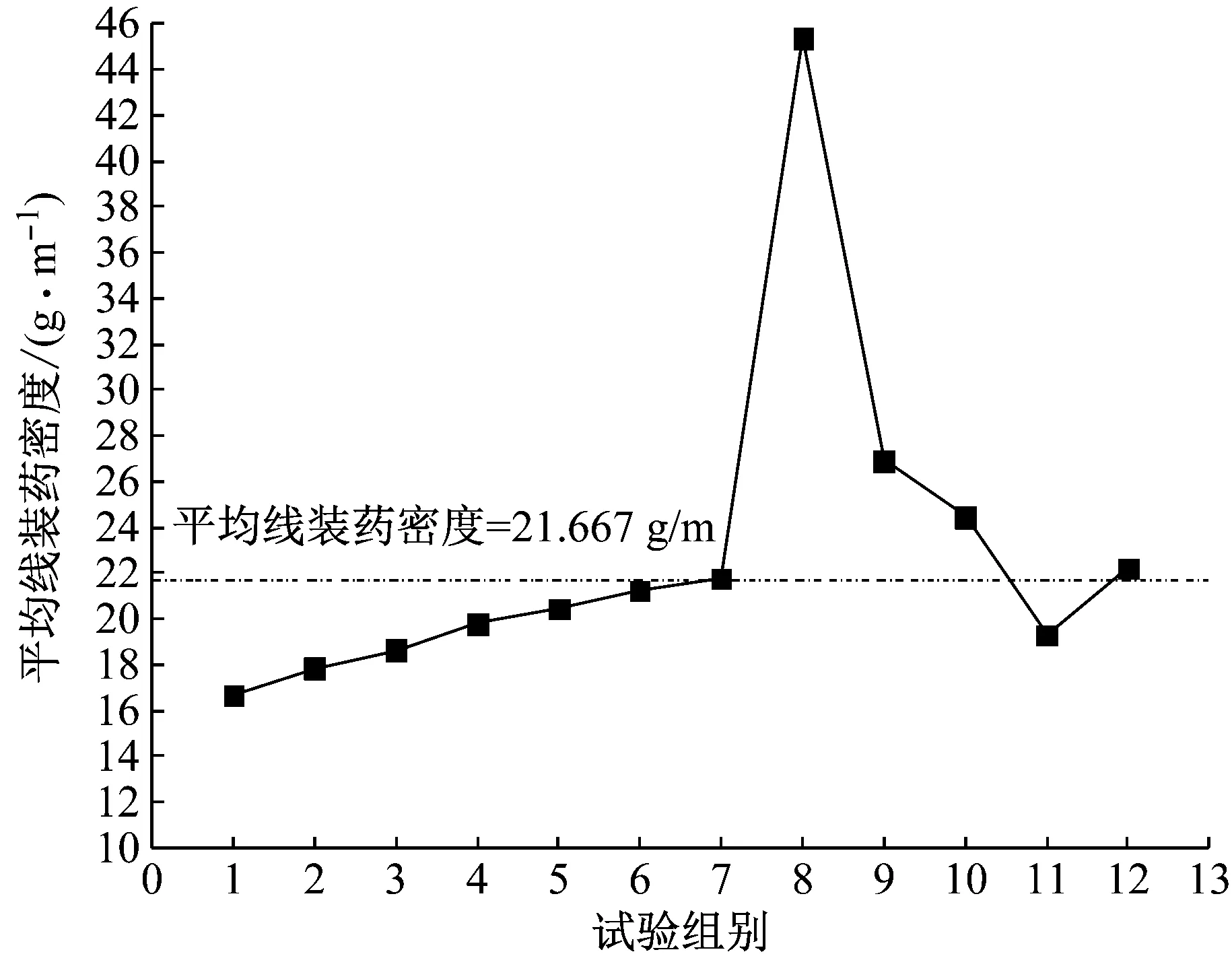
图8 平均线装药密度变化曲线

4 结 论

本文通过量纲分析方法，从主要影响因素中抽象出此现象的几何相似律，在几何相似律的基础上，通过计算机模拟预估试验参数，最后进行试验对爆炸分离钛合金板进行研究，结论如下：

(1) 在本文工况下，使钛合金板恰好分离的试验药量2.612 g，与模拟药量2.081 g较为接近，表明模拟结果对试验设计和进一步的数值模拟有指导意义。

(2) 采用不耦合装药且当d∶φ∶δ=10∶26∶7时，钛合金板能达到理想的分离效果。

(3) 通过本文的研究思路，仅用12次试验即得到了恰使合金板分离的药量，大大缩减了试验量，表明了研究思路的可行性，为此类爆炸分离装药量的进一步优化设计奠定了基础。