运用几何画板绘制椭圆的有效方法

于翠玲

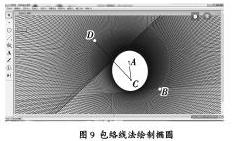
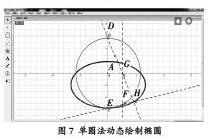
在圆锥曲线中，曲线上的点到定点的距离与到定直线的距离的商是常数e，且0

几何画板以点、线、圆作为基础图形，对这些基础图形进行拼接、平移、变换、度量、构造、轨迹追踪以及对基本图形的性质进行运用。学生可以在此过程中探究图形的内在关系并发现数学的本质，探究数学的奥妙和趣味性，激发学习数学的兴趣。笔者结合自身教学经验，在总结、归纳、提炼和创新的基础上整理出七种常用的运用几何画板绘制椭圆的方法，分享如下：

一、定义法

定义法的原理是圆锥曲线的统一定义，即焦点距离与到准线距离的商是定值的点的轨迹。椭圆的定义，即平面内一个动点到两个定点的距离之和等于常数，这个动点的轨迹叫椭圆，这两个定点叫椭圆的焦点，两焦点的距离叫作椭圆的焦距。

绘制的具体步骤为：打开软件，新建文件，在绘画板内画线段AB的同时在AB上绘制出C点，然后在AB外选取D、E两点，满足DE>AB;选中A、C两点进行标记向量，然后通过标记向量将D平移，得到D';选中D和D'点，绘制出一个以D为圆心，以D和D'间距离为半径的圆并且隐藏;同理，标记B、C两个点为标记向量，并且作出E的平移点到E'点，构造出圆，隐藏E'点;运用点工具做出两个圆周交点为F、G两点。

接下来分两种方法研究。

分别选中F、C和G、C两组点进行构造轨迹绘制出椭圆曲线，如图1所示。

点击F点，点击显示、追踪交点，同理操作G点;点击C点，选择操作类按钮、动画、确定，完成设置;点击绘画板上的动画键，绘画板就绘制出一个椭圆，如图2所示。

二、准线法

准线法的原理是圆锥曲线的统一定义，也就是到定点与定直线的距离的比为常数e的点的轨迹，叫圆锥曲线，而这条定直线就叫做准线和椭圆准线定义，即垂直于长轴所在直线的直线，方程为：

具体步骤为：打开软件，定义坐标系并且将原点设置为A点;用左侧工具栏中工具作出线段CD并做E点于CD上;同时选中C、E，并测量出CE长度，同理将CD长度测量出来;打开计算器并且输入CE/CD，然后双击出现的CE/CD的属性框，在比值标签中输入e并点击确定;在坐标系的横轴上设置点F为焦点;任意作出线段GH的同时取点I，然后度量出GI距离，并将GI的标签名称改为c;点击e和c两个数据框，然后打开计算器并且输入c/a，并将它的标签名称改为a;选中a在x轴上绘制点，并通过绘制点进行构造、垂线的操作，作出一条横坐标为a且垂直于x轴的直线;点击c，然后点击变换、标记距离;选中F点并且点击变换、平移、确定作出F'，选中F和F'两点然后进行作图、画圆;将直线和圆周的交点分别设为J、K并且选中两点进行追踪;点击I，进行动画操作，然后点击出现的动画按钮，椭圆的绘制动画就出来了，如图3所示。

三、同心圆法

在几何画板中定义坐标系，并且绘制两个圆心为原点A的圆，其中内外圆半径分别为短轴和长轴的长，然后隐藏单位点和两个圆周上的控制点;作外圆的半径为AE，将AE与小圆的交点设为点F;选中E和x轴进行构造、垂线，作出过E且垂直x轴的直线，同理作出过F且垂直于y轴的直线，两直线的交点则命名为G。

接下来的步骤分两种方法进行。

点击G和E，然后进行作图、轨迹，就作出了椭圆曲线，如图4所示。

点击G，进行显示、追踪点，然后选中圆周上点E，进行编辑、操作类按钮、动画、点击确定，然后点击动画按钮，通过点G运动就会画出椭圆，如图5所示。

四、单圆法

单圆法的原理是椭圆的定义，即平面内一个动点P到两个定点F1  、F2  的距离之和等于常数，且满足│PF1│+│PF2│= 2a>│F1F2│，这个动点P  的轨迹叫椭圆。这两个定点叫椭圆的焦点，两焦点的距离叫作椭圆的焦距。

单圆法第一种做法：打开几何画板软件，作出一个圆并隐藏圆周上的控制点B，该圆的半径为2a;在圆内和圆周上分别作出C、D两点，连接CD;选中CD构造出中点E，然后选中點E进行构造、垂线作出垂直CD的直线k;连接AD，然后作出k和AD的交点为F点;选中点F进行显示、追踪点F;点击D进行设置动画并点击完成键，绘画板上出现动画按钮，然后点击动画按钮，通过点D的运动绘制出椭圆曲线，如图6所示。

单圆法第二种做法：新建文件、定义坐标系并将原点设置为A，隐藏单位点并用工具画一个以原点为圆心的圆并且隐藏圆周上的点，然后将y轴和圆的交点设置为D、E，并在圆上作出F点;运用直线工具，做出线段EF，点击点F和纵坐标轴，然后构造、平行线，得到过F平行于y轴的直线，并将该直线与x轴交点设为G，连接D、G并作出EF和DG交点为H;点击H，然后显示、追踪点;点击F，点击编辑、操作类按钮、动画、确定，将出现动画按钮，点击该按钮，点H就会画出椭圆， 如图7所示。

五、三角形法

三角形法的原理与定义法基本相同，由于三角形边长不变，通过三角形一点在y轴运动带动其他点绘制出椭圆，只要是相交的两条直线就可以作出椭圆，不一定要选择坐标系的x轴和y轴;可以不选择正三角形，只要是可以固定形状不变就可以了。

首先新建文件，然后定义坐标系，将原点设置为A，单位上的点为B，并且将单位点B隐藏，运用线段工具作出任意线段CD;在y轴上x轴的两边分别作出E、F两点，且AE>CD和AF>CD;然后在作出EF的同时在y轴上做出G点，且AG

六、包络线法

包络线法的原理与单圆法基本相同，但是运用的方法类似于圆的切线，运用该方法得出的图形是切线未过的地方，因为椭圆图形任何一条切线都不可能经过椭圆内部。

新建文件，用圆工具作圆，将圆心设置为A，在圆内设置C点，在圆上设置D点，并连接AC、CD;设置CD的中点为E，作出过E垂直于CD的直线;选中垂线的同时，点击显示、追踪直线;点击D，进行编辑、操作类按钮、动画，然后确定;点击出现的按钮就会画出椭圆，如图9所示。

七、切线法

切线法的原理与单圆法基本相同。

打开几何画板并定义坐标系，将原点设为A;然后以原点为圆心作圆并将圆的控制点隐藏;运用点工具绘制将x轴与圆周的交点设置为D、E;然后在D、E两点作出x轴垂线分别为j、k;在圆上取F，并且连接FA，在F点做出圆的切线，隐藏FA，将G和H设为该线与j、k交点;连接线段GE、HD，将两直线交点设置为I，并且隐藏FA;将点I设置为追踪点并用 F设置动画，点击确定，点击左上角新出现的按钮，通过点I的运动就会画出椭圆，如图10所示。

以上绘制方法易教易学，便于操作。教学定法并非无法，只要我们在教学中善于观察和积累，把一些好的教学点滴记录下来，进行归纳总结和提炼，就会形成好的教学方法并逐渐形成自己的教学特色，服务于课堂教学。各位同仁不妨一试。

                                            编辑/王一鸣 E-mail：51213148@qq.com