高中生三角函数解题中典型错误的分析

罗雨薇，张玉娟

(鞍山师范学院 数学与信息科学学院，辽宁 鞍山 114007)

高中学生在数学学习中将面临更复杂且严密性、逻辑性更强的数学知识.随着函数内容学习的不断深入，有的学生在函数知识方面频频出现错误，有的学生同一类问题多次犯错误，这些错误在一定程度上打击了学生学习函数的积极性和自信心，使学生有可能丧失学习数学的信心.在三角函数的学习中，学生做题出错更是频繁出现.究其原因：学生在初中学习三角函数知识的时候，大都是直接带入公式就可以解题，步入高中阶段，三角函数的学习从锐角三角函数直接到任意角的三角函数，并且三角函数公式较多，很多学生面对这么多的公式无从下手，这就对学生的综合分析能力提出了较高的要求.更为复杂的是，对三角函数相关题目，需要学生应用数形结合思想，同时也需要学生有很好的基础知识才能解决，这就导致了高中生在三角函数学习中时常出现做错题，使学生面对三角函数望而却步[1-6].由此，深入研究高中生三角函数学习中出错的原因，找到相应的解决策略就显得尤为重要.

1 三角函数概念出错

学生学习任何新的知识时，首先学习的是概念，没有理解概念中的条件，导致学生在做有关三角函数概念题时出错.教师讲解概念时，应注意将概念中给出的条件重点讲解，使学生透彻理解概念.

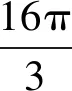
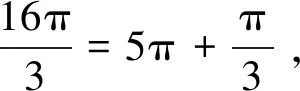
分析终边相同的角是指具有共同始边与终边的角.本题错误的原因是学生没有正确理解终边相同角的概念，本应该终边相同的角是该角加上2π的整数倍，学生误认为终边相同的角是一个角加上π的整数倍.

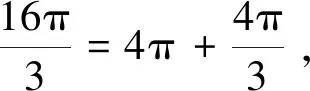
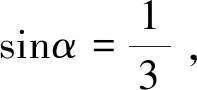
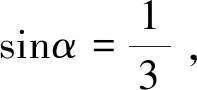
分析学生没有正确理解余弦函数的概念，忽视cosα可能取负值，导致此题做错.

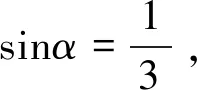
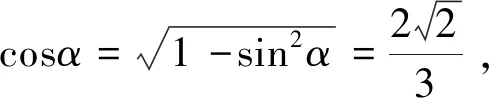
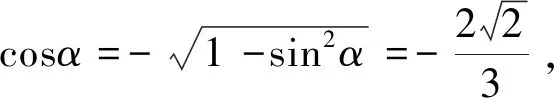
2 三角函数性质出错

高中三角函数的性质比较多，有定义域、值域、单调性、奇偶性、对称性、周期性等，正余弦性质容易混淆，并且容易忘记正余弦函数的有界性，所以学习和理解起来相对困难.

例3求解y=sinx+cos2x的值域.

错解y=sinx+cos2x=sinx+1-2sin2x，令t=sinx，则

分析学生出错原因是把t的值取为全体实数，因为t=sinx，也就是学生把sinx的值域取为全体实数，忽视正弦函数的值域，sinx∈[-1,1]，导致此题做错.

正解y=sinx+cos2x=sinx+1-2sin2x，令t=sinx，则

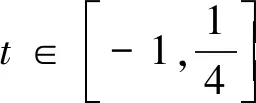
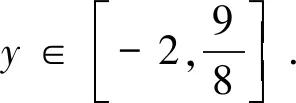
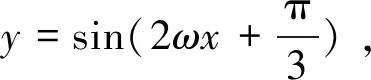
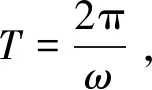
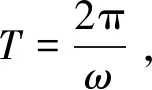
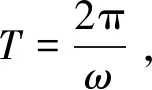
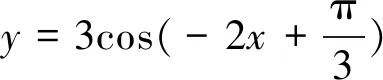
错解因为y=cosx的单调递增区间为[2kπ,2kπ+π],k∈Z，所以

得

分析学生出错原因在于没有先利用诱导公式化简函数解析式，而是直接用余弦函数单调性来求解单调区间，导致此题做错.

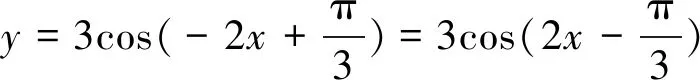
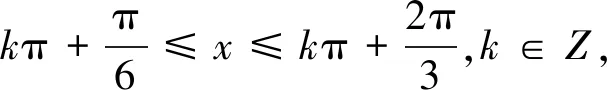
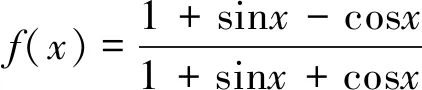
错解

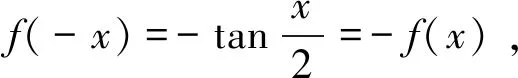
分析判断一个函数的奇偶性，首先应该考虑该函数的定义域是否关于原点对称，并且在求定义域时不能用化简之后的式子去求定义域，学生出错的原因是在化简的过程中改变了函数的定义域，导致此题做错.

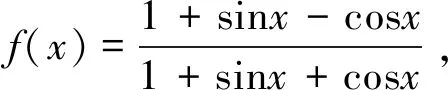
3 三角函数图像出错

三角函数图像可以更直观表示三角函数的单调性、周期性等，但学生利用三角函数解题时，经常把正余弦图像混淆，有的甚至不会利用函数图像去解题.

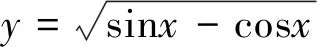
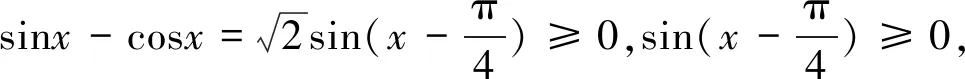
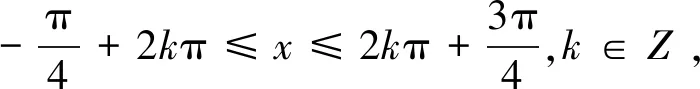
分析正弦函数在x∈[2kπ,π+2kπ],k∈Z区间上函数值大于等于0，余弦函数在

上函数值大于等于0，该题错误的原因是学生把正余弦函数图像混淆.

正解要想使函数有意义，则sinx-cosx≥0，所以

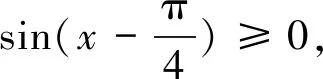
解得

所以定义域为

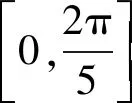
分析学生不能根据y=sinωx的图像把f(x)=sinωx的单调性与已知的两个区间联系在一起，导致学生没有思路，不知道如何去解此题.

4 三角函数综合应用出错

三角函数可以和二次根式、向量等进行综合应用，所以学生出错的表现大多是：知识点掌握得不牢固、计算马虎、综合能力比较差.

例9已知角α终边上一点P(-15a,8a),a∈R且a≠0，求角α的sinα,cosα,tanα的值.

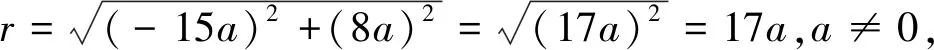
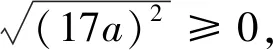
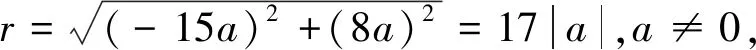
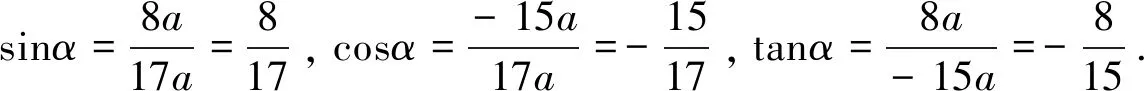
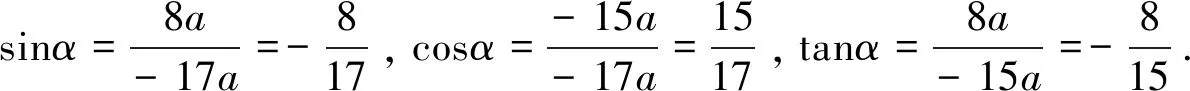
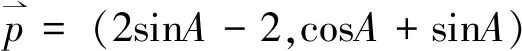
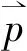
(2sinA-2)(sinA-cosA)+(cosA+sinA)(1+sinA)=0，

2sin2A-2sinAcosA-2sinA+2cosA+cosA+cosAsinA+sinA+sin2A=0，

整理得

3sin2A-sinAcosA-sinA+3cosA=0.

做到此处，大多学生算不出来了.

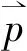
(2sinA-2)(1+sinA)-(cosA+sinA)(sinA-cosA)=0.

2sinA+2sin2A-2-2sinA-sin2A-cos2A=0，

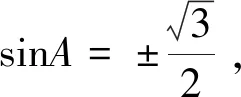
5 结 语

综上所述，在解三角函数题的过程中，为了防止学生出现解题错误，我们给出以下建议：

5.1 对教师的建议

(1)教师在讲解三角函数概念时，利用学生初中学习过的锐角三角函数知识，进一步深入引导学生学习三角函数的概念.学习概念时最重要的是让学生真正地理解，教师应该注意将概念中给出的条件做重点讲解，使学生能透彻地理解概念.

(2)三角函数性质图像比较多，学生经常通过死记硬背的方法来记忆，导致学生对三角函数中正余弦图像、性质混淆.教师可以利用多媒体向学生们展示三角函数的图像，通过图像可以让学生更直观地理解三角函数的单调性、单调区间、奇偶性等.这样可以加强学生对三角函数图像、性质的记忆，减少错误的产生，培养学生数形结合的数学思想.

(3)三角函数与二次函数、向量等有关知识进行综合应用，学生经常对已经学过的知识掌握不牢固，教师在讲授过程中，应该结合旧知识来引入新知识，使旧知识贯穿于新知识中，加深学生对知识的记忆，并且对其进行针对性练习.

5.2 对学生的建议

(1)在做有关三角函数概念题时，应该注意概念成立的条件.

(2)在做有关三角函数性质和图像的题时，学生习惯用二次函数求值方法，但是忽略正余弦函数的有界性，如文中例3所述，所以学生在求解有关三角函数极值或值域问题时，应该考虑在正余弦有界性的基础上，通过二次函数方法求值；学生解题时对三角函数中正余弦性质、图像混淆，如文中例7所述，所以学生应该多尝试先画正余弦函数图像，熟能生巧，而且直观地找出函数的单调区间等.然后在做题时结合正余弦函数图像，可以减少错误的发生.

(3)在做有关三角函数与其他知识综合应用题时，应该注意在学习新知识时不忘回顾旧的知识.并且多积累综合类型的三角函数题，可以使学生牢固掌握知识点，逐渐提高综合解题能力，减少差错.