机械臂的区间二型模糊超螺旋滑模控制*

张 双，赵 涛，佃松宜，胡 怡，江 浩

0 引 言

机械臂系统是一个十分复杂的多输入多输出非线性系统，具有时变、强耦合以及非线性的动力学特性[1].由于存在结构不确定性导致的建模误差，执行过程中的外部扰动等因素，使这一非线性系统的控制显得较为困难，故而对机械臂控制系统的研究具有重大的意义.

在机械臂控制系统中，为了使机械臂快速准确的到达指定位置，需要解决不确定性条件下机械臂的轨迹跟踪问题.针对机械臂系统的控制问题，目前已提出了PID控制[2-3]、计算力矩控制[4-5]、自适应控制[6-7]、鲁棒控制[8-9]、滑模变结构控制[10-11]和智能控制[12-13].滑模控制对参数摄动和不确定性扰动具有鲁棒性和响应快速的特点，与其他算法相比设计简单且易于实施.但是当在滑模面上运动的时候，容易产生抖振.超螺旋算法具有降低抖阵，补偿不确定量、有限时间内收敛的优点，是一种有效降低抖阵的算法[14].文献[15]和文献[16]设计了超螺旋滑模控制器来提升系统的控制效果，但是其参数是固定的，不能够随着系统状态的变化自适应的改变参数，这使得降低系统抖阵能力受参数限制.模糊控制由于其在处理复杂不确定非线性系统的优越性在近20年以来得到了快速发展.一型模糊由Zadeh教授提出以解决建模不确定性的问题，但是其在处理不确定性方面能力有限.因此Zadeh又提出二型模糊的概念[17]，为了降低二型模糊的计算复杂度Mendel提出区间二型模糊的概念，这使得二型模糊系统得到了快速发展[18].文献[19]和文献[20]展示了区间二型模糊相比于一型模糊在处理不确定性问题上的优越性.

模糊滑模控制可以结合模糊和滑模的优点来降低抖阵，提升非线性复杂系统的鲁棒性.文献[21]-[23]采用模糊控制来调整滑模控制器的输出，但是由于未考虑模型不确定性导致降低抖阵的效果有限.考虑到模糊控制的全局逼近性能，文献[24]针对机械臂的摩擦项采用模糊系统逼近，设计滑模控制器进行控制；文献[25]采用区间二型模糊对机械臂模型信息进行全局逼近，采用滑模控制进行控制.但是它们设计的滑模控制器都太过简单导致快速响应性能得不到满足.于是，文献[26]采用一型模糊逼近系统的非线性动态部分，设计基于梯度下降的终端滑模控制器进行控制；文献[27]采用模糊神经网络进行逼近，提出终端滑模控制器进行控制.尽管它们均获得了较好的轨迹跟踪性能，但终端滑模控制需考虑奇异问题，这使得控制器的设计复杂.

基于上述研究，本文的主要贡献有以下几个方面：(1) 针对文献[24]中一型模糊系统主要受隶属度函数选取的影响、逼近未知扰动精度有限和抗扰动性能弱的问题，提出基于自适应区间二型模糊系统对机械臂的不确定性进行逼近；(2) 针对文献[32]中基于超螺旋算法的趋近律参数固定，使得降低系统抖阵效果受参数限制的问题，本文采用一个改进的嵌套自适应律设计了基于超螺旋算法的趋近律，提出了超螺旋滑模控制器来保证系统的控制性能；(3) 针对文献[31]中基于嵌套自适应律的超螺旋趋近律稳定性证明复杂的问题，本文通过设置参数有界的假设条件，采用Lyapunov稳定性理论证明了趋近律的有效性，进一步导出了区间二型模糊逼近器的自适应律，保证了系统的稳定性.

1 问题描述

n自由度的机械臂系统由n个连杆和关节组成，基于拉格朗日方程和欧拉方程[28]，结合系统的摩擦项和外部扰动项，其动力学方程表示为

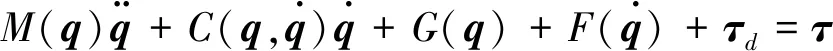
在实际生产中，考虑机械臂的建模误差、物理参数摄动等情况，动力学方程中的有关矩阵可表示为[12]:

式(4)即是后文设计控制方法的基础，这里要提出一个假设以便于后文研究的进行.

2 区间二型模糊逼近器

一型模糊逻辑和二型模糊逻辑十分相似，二型模糊对一型模糊中的隶属度进行了再次模糊化处理，所以在输出过程中存在一个降型的过程.就处理不确定性能力而言，二型模糊系统相比于一型模糊系统效果更佳[30]，而计算复杂度又低于广义二型模糊，因此选择区间二型模糊系统来作为逼近器.

区间二型模糊逻辑系统由以下规则来进行描述：

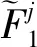
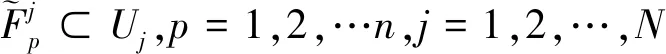
第j条规则的激活区间φj由下式计算：

采用Center-of-sets降型器来实现降型：

其中，yl和yr可以表示为：

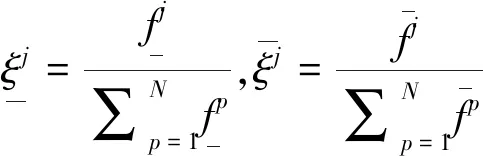
区间二型模糊系统的输出即为：

3 控制器设计

3.1 超螺旋滑模控制律

针对机械臂系统，控制目标为设计有效的控制器使各个转角位置q在有限时间内跟踪给定轨迹qd,定义系统跟踪误差:

e=q-qd(11)

定义滑模函数：

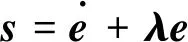
其中λ为正定矩阵，为了计算方便，定义辅助变量：

基于超螺旋算法，设计的趋近律如下：

其中，φ(t)是由如下的嵌套自适应律来设计[31]：

δ(t)的选取满足如下条件：

式中各参数的选择满足条件：

γ>0,ω>0,β0>0,η0>0,α>0(17)

假设2.κ(t)是一个有界函数，并且满足|κ(t)|≤α结合上述的分析，设计的控制器如下：

注1.本文删减了文献[31]中嵌套自适应律中的两个参数嵌套等式，增加了参数有界条件即假设2，未使用其相关成立条件.文献[31]中的控制对象为车辆线控转向系统，基于其一阶微分动力学方程，利用超螺旋算法进行控制器设计，而本文针对机械臂系统，基于超螺旋算法进行趋近律的设计.文献[32]中的κ(t)为一固定数值使得减小抖阵程度有限，本文则通过嵌套自适应律在尽可能减小抖阵效应的情况下自适应地调整调制增益，同时尽可能大的满足在有界不确定性条件下保持滑动.

由于双曲正切函数具有平滑性，为了进一步降低系统的抖阵，在本文将符号函数更换为双曲正切函数[33]：

y=tanh(s)(19)

因此式(18)可以表示为：

3.2 区间二型模糊自适应律

u(t)=

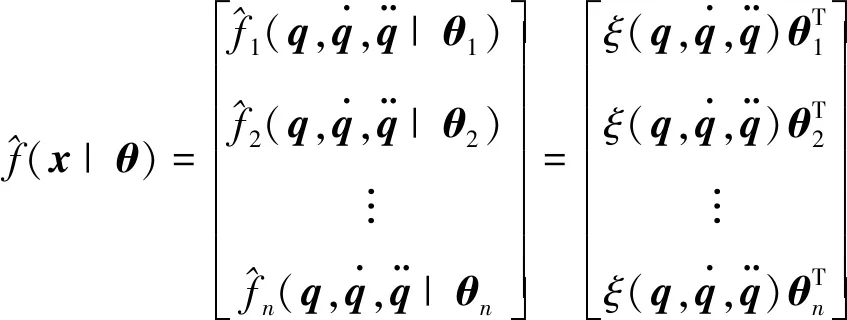
定义逼近系统的最优参数：

区间二型模糊逼近器的逼近误差表示为：

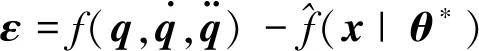
基于Lyapunov稳定性理论导出来的自适应律可以表示为：

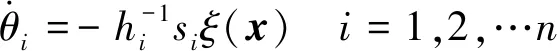
其中hi是正定矩阵H主对角线上的元素.

3.3 主要结果

图1展示了本文所提方法的控制框图.然后将本文的主要结果总结为如下的两个定理，它们分别说明了趋近律的有效性和控制器的稳定性.

图1 本文算法控制框图Fig.1 Control diagram of our proposed method

定理1.考虑趋近律(14)，结合嵌套自适应律(15)，在参数条件(16)、(17)成立的情况下，(14)所示的趋近律是可以到达滑模面(12)的.

证明.

定义Lyapunov函数：

对(26)式求导有：

β(t)(-|η0+η(t)|sign(β(t)))

所以基于超螺旋算法的趋近律是可以到达滑模面的.证毕.

定理2.考虑机械臂系统(4)，结合区间二型模糊逼近器输出(22)，在控制器(21)的设计下，定义的跟踪误差(11)可以在给定参考轨迹的情况下收敛到零.

证明.

定义Lyapunov函数:

结合式(11)～(14)、(18)式、(23)式、(24)式，对(28)式求导可以得到：

注2.定理2成立的条件是定理1成立.不同于文献[31]的基于嵌套自适应律结合Lyapunov定理证明系统稳定性,定理1成立的条件是基于假设2和条件(17)，(18).文献[32]κ(t)数值固定使得在稳定性证明中可以很容易证明稳定性，本文通过增加假设2使得证明亦相对容易，同时又使调制增益自适应改变，若无假设2则稳定性证明需要增加更多的参数限制.

为了评价系统的控制效果，采用四种评价指标[20]：ISE、IAE、ITSE、ITAE,它们的计算公式如式(30).

4 仿真研究

为了验证所提控制器的有效性，以二自由度机械臂为仿真研究对象，其动力学矩阵参数[34]为：

其中，机械臂的仿真参数选为：m1=1，m2=1.5，r1=1，r2=0.8，g=9.8.

对机械臂选取实验给定轨迹为：

qd=[sin(t) 0.8sin(t)]T

ΔM(q)=0.02M(q);

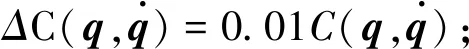
ΔG(q)=0.05G(q)

控制器的参数设计如表1所示.

为了验证本文算法的有效性，将本文算法与同一型模糊滑模控制[24]进行了比较，同时为了凸显区间二型模糊处理不确定性的能力和本文提出的超螺旋算法的有效性，在其中分别更换了模糊部分和滑模部分进行仿真分析.所以共有四种方法进行了比较，分别是一型模糊滑模控制(T1FSMC)、一型模糊超螺旋滑模控制(T1FSTSMC)、二型模糊滑模控制(IT2FSMC)和二型模糊超螺旋滑模控制(IT2FSTSMC).

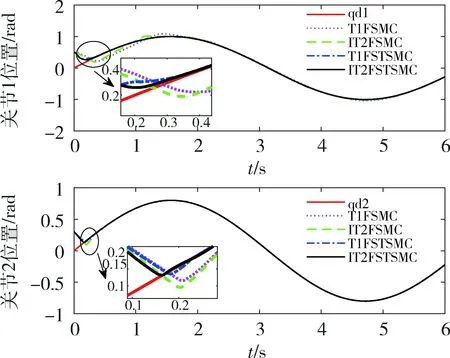
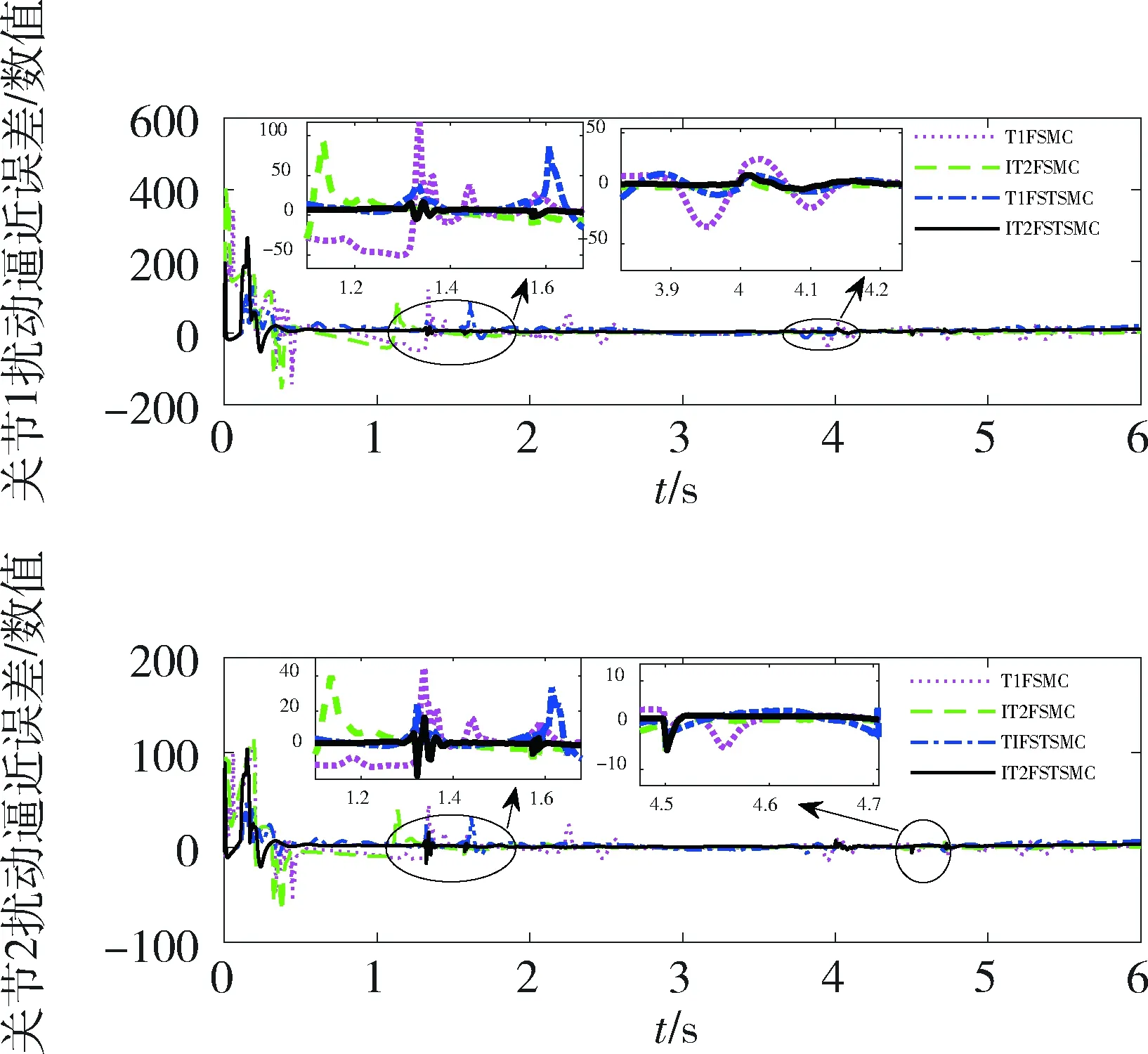
图2展示了四种控制方法对于同一条给定轨迹的跟踪效果，整体都能够在补偿扰动的情况下实现对于给定轨迹的跟踪，但从放大图中可以看出在系统的动态性能方面，超螺旋滑模控制提升了系统的响应速度，相比于传统的滑模控制，缩短了系统的响应时间，实现了快速跟踪；图3的0

表1 控制器参数Tab.1 Parameters of controller

图2 两关节角位置跟踪曲线Fig.2 Two-joint angular position trajectories

图3 两关节角位置跟踪误差曲线Fig.3 Trajectory tracking errors of two-joint angular position

为了进一步体现区间二型模糊对于广义扰动的逼近能力，图4展示了对于扰动的逼近效果，从0

图4 扰动逼近曲线Fig.4 Disturbance approximation curves

从之前的图中可以看出，提升控制效果的主要是超螺旋滑模控制，实现对给定轨迹的快速跟踪，而区间二型模糊则主要实现对扰动的逼近.因此，对于性能指标的评价主要针对T1FSTSMC和IT2FSTSMC,从跟踪误差曲线看误差主要存在于0

图5 扰动逼近误差曲线Fig.5 Disturbance approximation error curves

图6 性能指标曲线Fig.6 Performance index curves

为了进一步展示在控制过程中的累计误差情况，表2给出了性能指标结果，可以看出控制效果是IT2FSTSMC>T1FSTSMC>IT2FSMC>T1FSMC,其结果依然说明了采用区间二型模糊逼近广义扰动和利用超螺旋算法设计滑模控制器的有效性.

表2 性能指标结果Tab.2 Results of performance index

5 结 论

虽然模糊控制能够对任意非线性函数进行逼近，但是其隶属度函数影响了逼近的精度；滑模控制虽然能够保证系统的稳定性，但是其快速跟踪效果及抗干扰能力还需进一步提升.所以为了解决传统模糊滑模控制在不确定条件下鲁棒性弱的问题，本文提出了一种基于区间二型模糊补偿扰动的超螺旋滑模控制算法.首先，为了处理不同干扰，将系统内部扰动和外界干扰统一看作广义扰动，通过选取合适的隶属度函数来逼近广义扰动，使得在控制器设计的时候，能够补偿广义扰动带来的误差，提高系统的抗干扰性；然后基于超螺旋算法，设计了嵌套自适应律来对超螺旋算法中的参数进行自适应调节，提升系统响应的快速性和准确性；接着利用Lyapunov稳定性理论证明了趋近律的稳定性和系统的稳定性，并基于稳定性导出了区间二型模糊的自适应律实现对模糊系统的自适应调节；最后通过对2自由度机械臂进行仿真实验，验证了区间二型模糊的逼近性能和超螺旋滑模控制的鲁棒性，本文提出的方法能够提升系统的控制品质.