基于伪谱法的空间绳系组合体最优燃耗离轨研究*
李鹏杰,谈树萍,钟 睿
0 引 言
目前,空间碎片清理越来越受到国内外航天界的关注. 在所有可能的空间碎片清理方式中,空间绳系系统因为其具有质量轻、结构简单、可作用范围远等优点,是最有前景的空间碎片清理方式之一.主动星在完成拖拽目标进入目标轨道的任务中,由于主动星的载荷和续航有限,对离轨燃耗的优化是很有必要的;其次,通过传统的方法很难求解出组合体离轨最优控制问题的解析解,而伪谱法求解最优控制问题收敛速度快,精度高,对初值敏感度低,使用伪谱法对绳系组合体离轨最优控制问题进行研究具有积极的意义.
对绳系组合体动力学和控制的研究已经经历很长一段时间,有了一系列成熟的理论和成果. MODI等[1]在1980年提出极具一般性的绳系系统动力学模型,不仅考虑了系绳分布质量、空间位形,还考虑了系绳和航天器连接点的偏置,得到了复杂的微分方程. 2001 年欧空局提出了地球静止轨道碎片清理器(ROGER,robotic geostationary orbit restorer)项目[2],该项目提出的控制策略能有效地抑制组合体离轨过程中系绳的摆动. 在绳系组合体离轨优化方面,LIU 等人[3]提出了加速、平衡、旋转、返回四阶段组成的地球同步轨道上废弃卫星拖曳离轨方案,仿真表明方案可行,并能够节省整个过程的燃耗. ZHONG等人[4]设计了与最优控制结合的电动力绳系微小卫星的快速拖曳离轨方案,该方案能够将系绳摆动限制在允许的范围内,并实现电动力绳系微小卫星的快速离轨.
本文同样与最优控制结合,设计了拖拽、稳定、甩摆三个离轨过程. 拖拽过程采用最优控制方法,目的是最优化离轨全过程燃耗. 拖拽完成后组合体以垂直构型到达转移轨道,在转移轨道上主动星关闭推力,借助重力梯度作用经过一段平衡过程到达甩摆点. 甩摆点上主动星通过推力作用获得一定量冲量,将目标星甩到能够到达目标轨道的速度后切断系绳. 本文提出了适用于伪谱法求解的绳系组合体简化动力学模型,通过伪谱法求解得到系统状态最优轨迹;然后考虑更加精确组合体动力学模型,并考虑主要外界干扰,设计了模型预测控制器来跟踪系统状态最优轨迹,实现了组合体燃耗最优离轨的闭环控制.
1 绳系组合体动力学建模
绳系组合体由主动星、目标星和连接于两星之间的系绳组成. 对于本文所使用的绳系组合体动力学进行建模,模型采用常用的哑铃模型,考虑组合体三维空间的轨道运动和系绳在轨道平面内和轨道平面外二维的摆振运动,并做出如下假设:1) 主动星与目标星视为质点,系绳视为只可承受拉力的刚性杆;2) 系绳长度固定,忽略组合体质心与重心的差异;3) 组合体运动分解为质心的轨道运动和绕质心的摆振运动.

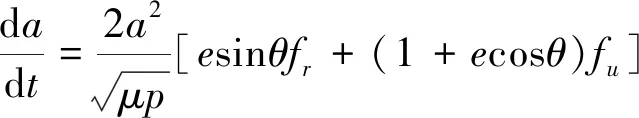
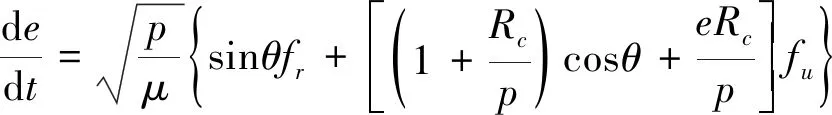
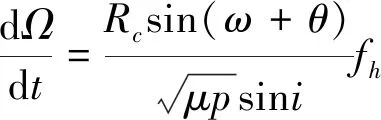

(5)
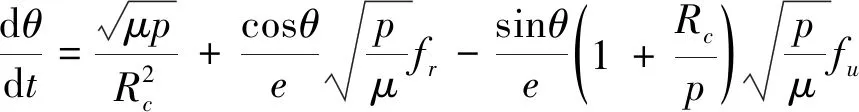
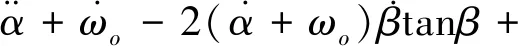
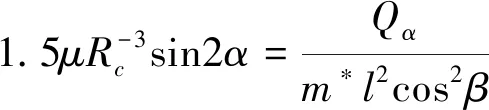
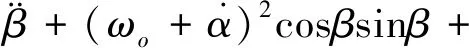

Fte=Ql+
(9)
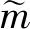

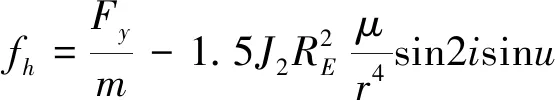
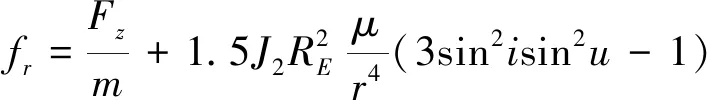

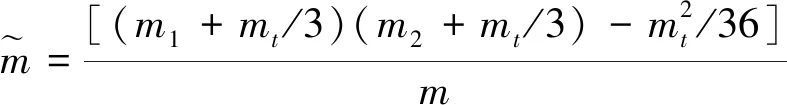
式中,m为系统质量,m=m1+m2+mt.J2,RE为地球扁率系数和地球半径,均为常值,J2=1.082 63×10-3,RE=6.378 141×106m.r,i,u分别为系统质心到地心的距离、系统质心轨道倾角、系统质心轨道纬度幅角.
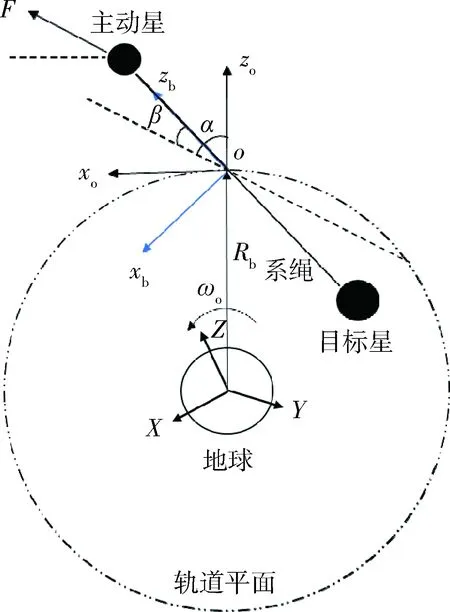
图1 三维空间绳系组合体模型Fig.1 Three dimensional TSS model
为了降低求解最优拖曳离轨控制问题的维度,对以上空间模型进行平面假设:1) 忽略系统在轨道平面外的运动;2) 忽略系绳的质量;3) 推力F作用于轨道平面内,与xo轴夹角为η;4) 不考虑地球扁率及其他引力摄动. 由此可得到简化组合体质心轨道动力学方程、系绳摆振动力学方程以及系绳张力表达式为:
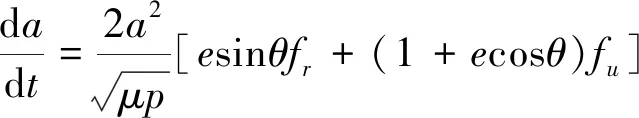
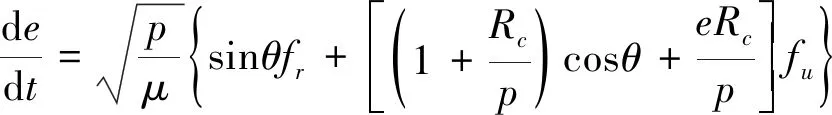
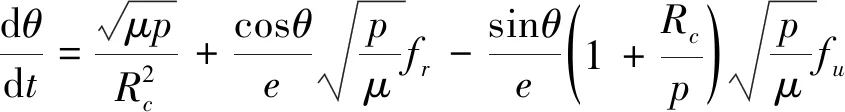

Fte,plane=m1m2m-1l×
Fm2m-1sin(η+α)(19)
zo轴和xo轴方向的摄动加速度fr和fu表达式为fr=Fsinη/m,fu=Fcosη/m.Fte,plane为平面假设模型下系绳张力大小.
2 组合体离轨方案设计
2.1 问题描述
空间绳系组合体进行轨道机动转移,需要面临三大主要风险:一是系绳张力过大引起的系绳断裂,二是系绳松弛引起的两星相撞,三是目标星自旋或章动以及系绳剧烈的摆动引起的系绳缠绕. 本文将主动星和目标星视为质点,不考虑两星姿态运动对于组合体离轨的影响. 如何避免上述组合体离轨所必须面临的风险,是本文方案设计的重点考虑因素. 参照空间碎片协调委员会(IADC)对地球同步轨道(GEO)上空间碎片处理的建议[7],本文提出的组合体离轨方案目标为将目标星送入近地点高于GEO高度350 km的坟墓轨道.
2.2 设计思路
如图2所示,该组合体轨道转移方案可分为三个阶段:
(1) 拖拽. 基于高斯伪谱法求解组合体在主动星推力作用下从GEO拖拽至转移轨道的燃耗最优控制问题. 最优控制问题优化指标为离轨三个阶段总的燃耗,由于到达的转移轨道确定了,第三阶段甩摆所需要的燃耗也可确定. 拖拽结束后到达的转移轨道为远地点高于GEO高度350 km的椭圆轨道. 求解得到系统最优状态轨迹,通过对最优轨迹的跟踪控制,组合体完成拖拽阶段,并以垂直构型且面内摆动速率为零进入下一阶段.
(2) 平衡. 主动星关闭推力,借助重力梯度作用以及适当的控制作用,组合体保持垂直构型在转移轨道上做轨道运动,最终到达转移轨道的远地点. 本文忽略该阶段的燃耗.
(3) 甩摆. 组合体到达转移轨道远地点后,通过主动星推力作用,主动星在很短的时间内获得一个水平方向的冲量,组合体进行甩摆.甩摆发生180°,主动星与目标星进行动量交换,目标星到达期望的离轨速度,此刻剪断系绳,目标星进入轨道半径高于GEO高度350 km的圆轨道,满足坟墓轨道要求.

图2 离轨三阶段示意图Fig.2 Three phases of TSS deorbit
2.3 拖拽阶段最优控制求解
随着计算机技术的不断发展,最优控制问题的求解逐步由解析方法向数值方法转变. 近年来,伪谱法在众多直接法中发展较快. 迄今为止,伪谱法已经应用于解决无人机航迹规划、导弹制导、机械臂轨迹优化、倒立摆的稳定、航天器轨道机动和入轨飞行器上升段制导等大量最优控制问题[8-12],成为目前解决最优控制和轨迹最优化问题最有效的工具.
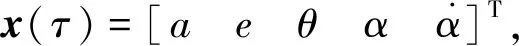
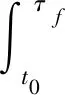
其中,式(20)加号左边积分项为第一阶段的燃耗,加号右边为第三阶段甩摆主动星需获得的冲量,其中m1为甩摆阶段主动星的质量,表达式为:

式(21)中Δm为第一阶段消耗的燃料质量,Isp为推力器比冲.
为对于第三阶段甩摆,将该阶段时间视为足够短,主动星质心的轨道没有变化,该过程除了受到恒定地球引力外不受其他外力干扰.对组合体从垂直构型到甩摆180°该过程,根据动量定理和角动量定理有:
m1(v1+Δv)+m2v1=m1v1+m2v2(22)
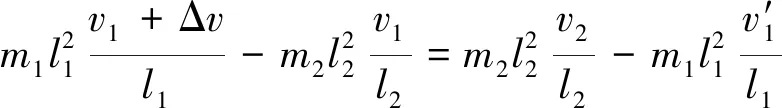

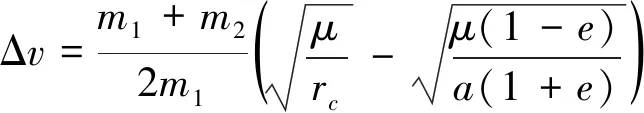
式中,rc为目标圆轨道半径,μ为地球引力常数,a、e分别为转移轨道半长轴和偏心率.
该组合体离轨最优控制问题动力学约束为式(15)~(18),状态初值和末端条件为:
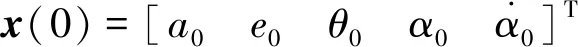
a(τf)(1+e(τf))=rp,grave(26)
其中rp,grave为坟墓轨道近地点半径,即转移轨道远地点半径.考虑到离轨面临的三大主要风险,对系绳张力大小、系绳面内摆角及摆角速率施加约束.边界条件和非线性约束为:
xmin≤x(τ)≤xmax(27)
umin≤u(τ)≤umax(28)
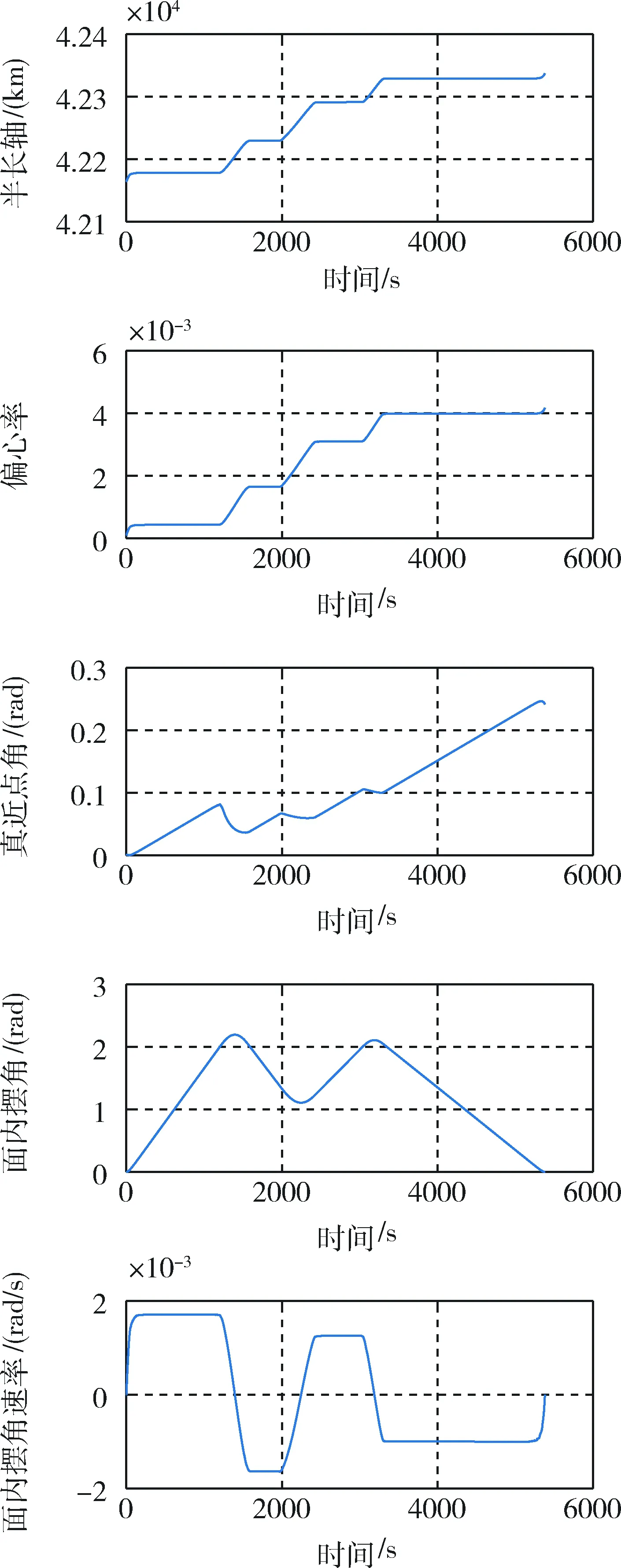
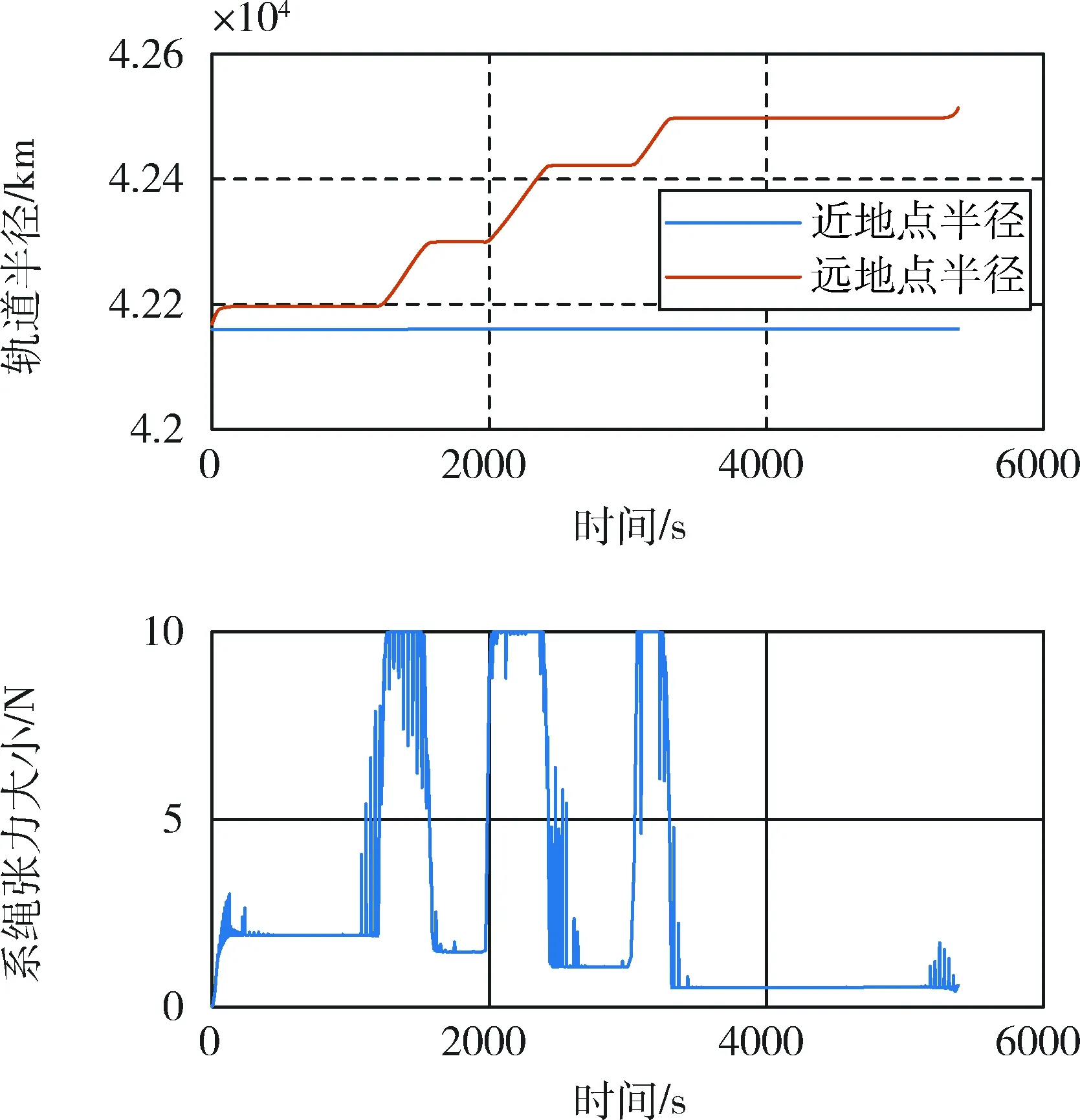
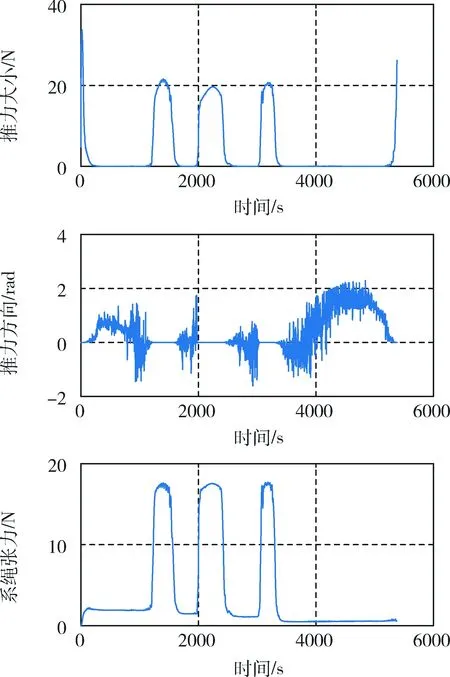
0 该最优控制问题使用MATLAB最优化求解工具箱GPOPS进行求解,获得离轨全过程燃耗最优,拖拽段的状态和控制最优轨迹. 由于模型的不精确性以及外界干扰的存在,所得到的开环最优控制轨迹无法直接用于控制组合体完成拖拽段到达转移轨道,于是设计模型预测控制器闭环控制消除系统状态偏差. 闭环控制的系统模型采用式(1)~(7)推导的较为精确的系统模型,并考虑地球扁率带来的引力摄动. 模型预测控制方法是基于最优化的反馈控制方法,在每一个采样时刻k的优化指标为: G(U(k))= 0≤k≤τf,0 xmin≤x(k+i)≤xmax(31) Umin≤U(k+i)≤Umax(32) x(k+N)-xopt(k+N)=0; 0 其中式(31)、式(33)对系绳面内摆角、面内摆动速率以及张力大小进行约束,避免离轨三大风险.式(34)保证了模型预测控制器的稳定性. 需要说明都是模型预测控制器中预测模型仍然是平面假设下的简化模型. 绳系组合体物理参数见表1,开环最优控制问题求解仿真参数见表2,闭环模型预测控制仿真参数见表3. 表1 绳系组合体物理参数Tab.1 Space tethered system physical parameters 表2 最优控制问题约束参数Tab.2 Constraints in the open-loop optimization 表3 模型预测控制仿真参Tab.3 Constraints in MPC 图3 拖拽段状态量开环最优轨迹Fig.3 Open-loop optimal trajectories of state variables in dragging phase 图3和图4给出了拖拽段系统状态变量和控制变量的最优轨迹. 图5给出系统质心近地点半径和远地点半径变化曲线,以及系绳张力的变化曲线. 图3中可以看出轨道半长轴和偏心率以一致的趋势增加,系绳的面内摆动速率控制在±2×10-3rad/s范围内,面内摆角在[0,2.3]rad范围内变化. 图4中可以看出推力大小限制在50 N以内,并且推力沿着轨道运动方向. 图5中可以看出系统质心轨道近地点半径不变,远地点高度持续提升至坟墓轨道近地点半径高度,并且在整个过程中系绳的张力在[0,10N]范围内. 优化后的总燃耗为3.318 7×104kg·m/s,为同质量单体航天器进行霍曼转移从同步轨道到达坟墓轨道所需燃耗的74.8%. 图4 拖拽段控制量开环最优轨迹Fig.4 Open-loop optimal trajectories of control variables in dragging phase 图5 轨道近地点半径和远地点半径以及系绳张力大小随时间变化曲线Fig.5 Times histories of orbital perigee and apogee and tether tension 图6 拖拽段系统质心轨道要素变化曲线Fig.6 Times histories of orbital elements of TSS’ center of mass in dragging phase 图7 拖拽段系绳面内面外摆角和摆角速率变化曲线Fig.7 Times histories of tether in-plane and out-of-plane libration angle and angular velocity in dragging phase 图8 拖拽段系推力大小和方向以及系绳张力大小变化曲线Fig.8 Times histories of closed-loop control variables and tether tension 图6和图7给出了系统在拖拽段状态变量的跟踪情况,以及系统质心另外三个轨道要素变化情况和系绳面外摆动情况,可以看出模型预测控制器能跟踪上最优轨迹. 图8给出闭环控制量推力和推力方向变化曲线,以及系绳张力变化情况. 从图7、图8中可以看出系绳面内、面外摆动速率被限制在一个很小的范围内,系绳张力大于零,系绳保持张紧,避免了离轨的三大风险. 拖拽段闭环所用燃耗为2.260 9×104kg·m/s,由式(24)计算出甩摆段所需燃耗为1.067 8×104kg·m/s,全过程所需燃耗为霍曼转移的75%. 比霍曼转移更节省燃耗的原因主要是系绳的动量交换特性,在甩摆阶段主动星将部分轨道能量转移到目标星上,最终只消耗主动星75%霍曼转移燃耗就能够将目标星送达坟墓轨道,而主动星到达转移轨道附近. 组合体结束拖拽段后进入平衡段,主动星推力关闭. 仿真表明,平衡段组合体借助重力梯度作用,系绳张力比较小,在一定初值范围,组合体垂直构型以及张力大于零可以维持,如考虑外干扰,需要引入防松弛控制,不在本文范畴,在后续工作中将进一步研究. 本文提出一种基于伪谱法求解的绳系组合体最优燃耗离轨方案,通过拖拽、平衡、甩摆三个阶段可将目标星以最优的燃耗转移至坟墓轨道. 对拖拽段仿真表明该方法能够利用系绳动量交换特性以75%霍曼转移的燃耗实现目标星的轨道转移,并避免了三大风险. 但本文缺乏平衡段面内摆振镇定和甩摆段的仿真,有待于进一步改进.2.4 模型预测控制器设计
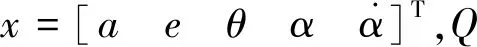
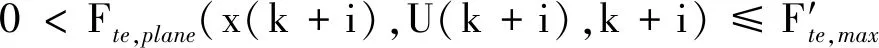
3 仿真分析
3.1 仿真参数



3.2 拖拽段开环最优轨迹

3.3 模型预测控制仿真


3.4 平衡段运动说明
4 结 论

