基于近端策略优化算法的四足机器人步态控制研究*

张浩昱，熊 凯，2

0 引 言

随着机器人的应用越来越广泛，对机器人智能程度的要求也逐渐提高.传统的机器人控制方法在复杂的动态未知环境中的应用存在很大的局限性，深度强化学习方法结合了强化学习的决策能力和深度学习的感知能力，智能体可以像人类一样通过环境交互进行自主学习，为实现机器人的智能控制提供了全新的研究思路[1].

强化学习在实际应用过程中往往会遇到参数更新步长难以选择的问题，步长选择过小会导致训练速度过慢；步长选择较大容易引起震荡，甚至导致算法不收敛，训练结果越来越差，因此有必要通过研究寻找一个合适的步长.针对这一问题，Schulman等提出了置信区域策略优化(TRPO)方法[2]，避免出现使参数改变很大的步长，并且使得获得的回报单调不减，即策略总是向更好的方向更新.在此基础上，Schulman又提出了形式更加简洁、训练效果更好的近端策略优化(PPO)算法[3]，在实际应用中展现出更好的鲁棒性.

本论文基于ROS机器人操作平台搭建了四足机器人仿真模型，对其步态控制进行任务建模，并设计了近端策略优化算法在四足机器人步态控制中的应用方法，并与深度确定性策略梯度算法进行了对比分析.

1 相关工作

1.1 强化学习

强化学习是借鉴了智能体与环境不断交互，不断获得经验知识，总结出更优化的策略的过程[4]，从本质上来说是一种试错学习的方式(trial-and-error)，这种学习方式不需要外界的监督，依靠智能体不断尝试，最终达到优化自身行为的目的(见图1).

图1 强化学习过程Fig.1 Reinforcement learning process

对强化学习的描述通常是基于马尔科夫决策过程(Markov Decision Process，MDP)[5]，其任务对应了一个四元数组E=,其中，S为状态集，A为动作集，P为状态转移概率，R为回报函数，通常使用累积折扣回报来定义在t时刻的状态回报，即

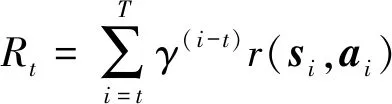
其中γ为折扣因子，表明越远处的回报对当前状态的评估影响越小，r(si,ai)表示在状态si选择动作ai所获得的回报值.设初始状态为s1,在某一策略π下，状态分布服从ρπ,则强化学习的任务为学习到一个策略π,使得期望的初始状态回报达到最大.定义强化学习目标如下：

J=Es～ρ,a～π[R1](2)

状态值函数Vπ(s)表示从状态s出发，执行策略π所带来的累积回报：

Vπ(st)=Es～ρ,a～π[Rt|st](3)

状态动作值函数Qπ(s,a)表示从状态s出发，执行了动作a后，再执行策略π所带来的累积回报：

Qπ(st,at)=Es～ρ,a～π[Rt|st,at](4)

时序误差方法[6]应用了动态规划的思想，用下一时刻的状态动作值函数来估计当前的状态动作值函数：

Qπ(st,at)=

Er,st+1～E[r(st,at)+γEat+1～π[Qπ(st+1,at+1)]]

(5)

其中r,st+1的分布服从于环境E，at+1的分布服从于策略π.

定义时序误差为

δt=rt+γQπ(st+1,at+1)-Qπ(st,at)(6)

在不需要指明特定的策略的情况下，Qπ往往可以直接使用Q来代替.

使用神经网络去逼近状态动作值函数，设网络的参数为θQ,可以定义网络的损失函数为

L(θQ)=Es～ρ,a～π[(yt-Q(st,at|θQ))2](7)

其中

yt=rt+γQ(st+1,at+1|θQ)

1.2 近端策略优化算法

强化学习的优化目标是使得回报最大，在策略梯度算法中[7]，网络参数θ更新的目标函数为：

L(θ)=E[logπ(at|st;θ)At(st,at)](8)

其中At(st,at)为优势函数，该函数定义为：

At(st,at)=Qt(st,at)-Vt(st)(9)

网络参数更新方式可表示为：

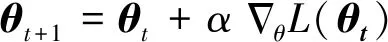
可以证明当新旧策略满足一定的约束时，可以使得策略是单调不减的，修改目标函数为：

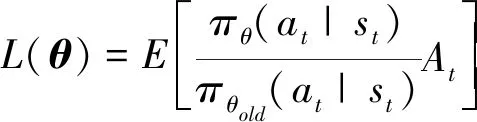
新旧策略的KL散度满足约束：

E[KL[πθold(at|st),πθ(at|st)]]≤δ(12)

其中δ是一个常数，KL散度用于衡量两个分布的差异程度，其值越大说明两个分布差异越大.

PPO中将约束项作为惩罚项引入目标函数，即修改目标函数为：

在实际应用中，研究人员发现使用截断项代替KL散度具有更好的效果.将新旧策略的比值记为：

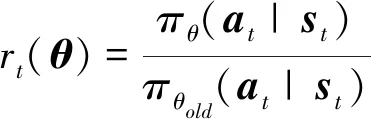
目标函数设计为：

L(θ)=

E[min(rt(θ)At,clip(rt(θ),1-ε,1+ε)At)]

(15)

其中ε为截断常数，其取值为一个经验值；clip函数为截断函数，将rt(θ)的值限定在1-ε和1+ε之间.PPO算法在进行参数更新的过程中，通过截断或限制KL散度的方式，避免策略出现突变的情况，增强了训练的效果.

2 四足机器人仿真环境搭建及算法应用

2.1 仿真环境搭建

本论文基于ROS机器人操作系统，在Gazebo物理仿真环境中搭建了四足机器人仿真环境，如图2所示.

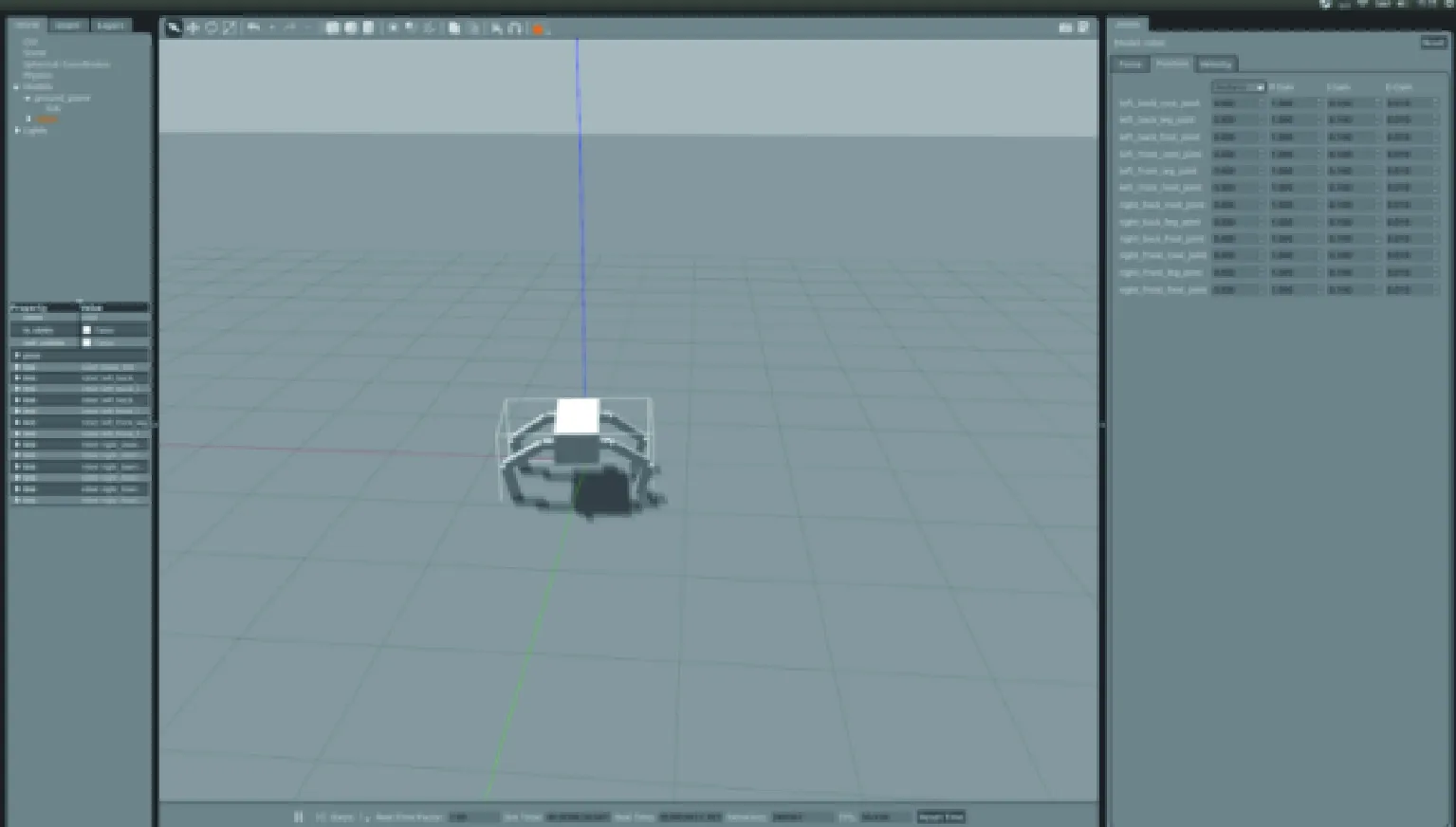
图2 四足机器人仿真环境Fig.2 Quadruped robot simulation environment

四足机器人结构如图3所示.四足机器人的每条腿上有三个关节，分别为髋关节的偏航关节qy和俯仰关节qp,以及膝关节qk,每个关节都可以通过电机输出力矩实现位置控制.深度强化学习可以实现端到端的控制方式，即实现直接从状态输入到底层的力矩输出，这种方式虽然简单，但是该算法在复杂的任务中很难学到有效的策略，因此本文在实际应用中，先由深度强化学习算法输出期望的关节位置，再由ROS中的电机驱动模块输出力矩，实现底层的位置控制.

图3 四足机器人Fig.3 Quadruped robot

2.2 任务建模

四足机器人步态控制要求机器人在没有先验知识的情况下学会行走，在单位时间内的位移尽可能大.在步态控制任务中需要实时控制机器人四条腿上每个关节的力矩输出，因此动作空间可设计为所有关节的期望位置，即

A=qT=[qyqpqk]T

=[qy1qy2qy3qy4qp1qp2qp3qp4qk1qk2qk3qk4]T(16)

动作空间的维度为12，即|A|=12.

对于状态空间的选择，本论文简单考虑机器人当下的决策仅仅和当前各个关节的状态有关，因此设计状态空间为

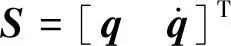
且|S|=24.

在此基础上根据任务需求设计机器人与环境交互过程中的回报函数.在四足机器人步态控制中，我们希望四足机器人能学会自主行走，实现在单位时间内位移最大，因此设计回报函数为

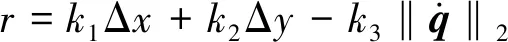
其中Δx表示沿x轴的位移，Δy表示沿y轴的位移，这两项表示希望机器人的位移尽可能大，第三项表示我们不希望机器人的关节位置有太大的变化，k1，k2，k3为权重系数，用于调整各项在总回报中重要程度，通过调整k1，k2的值可以设置机器人的前进方向，实现机器人在期望的方向上获得最大的位移.

2.3 实验结果

本论文不使用直接从状态输入到力矩输出的端到端的控制方式，而是将整个任务分为决策和控制两个部分，由深度强化学习算法输出各个关节期望的角度，并由底层的PID控制器实现位置控制，提升训练效果.四足机器人步态控制框图如图4.

如图所示，整个系统被分为被控对象、状态样本池、决策网络以及底层控制四个部分.被控对象即为四足机器人仿真模型.状态样本池用于存储机器人的历史状态，决策模块通过样本池中的数据进行学习.决策模块由策略网络和评价网络组成，策略网络根据当前的机器人状态进行决策，给出下一时刻机器人期望的关节位置；评价网络根据历史数据评价策略网络的性能，并指导策略网络进行参数更新，其更新方式可以使用不同的强化学习方法.底层控制模块是一个PID控制器，根据机器人当前的关节角度和期望的关节角度的误差及其变化率输出每个关节对应的力矩.

将近端策略优化(PPO)算法和深度确定性策略梯度(DDPG)算法[8]用于四足机器人步态控制实验，其中DDPG分为两种，一种是使用了优先级经验回放的改进DDPG算法[9]，一种是使用随机采样方法的传统DDPG算法， 并对实验结果进行了对比分析.

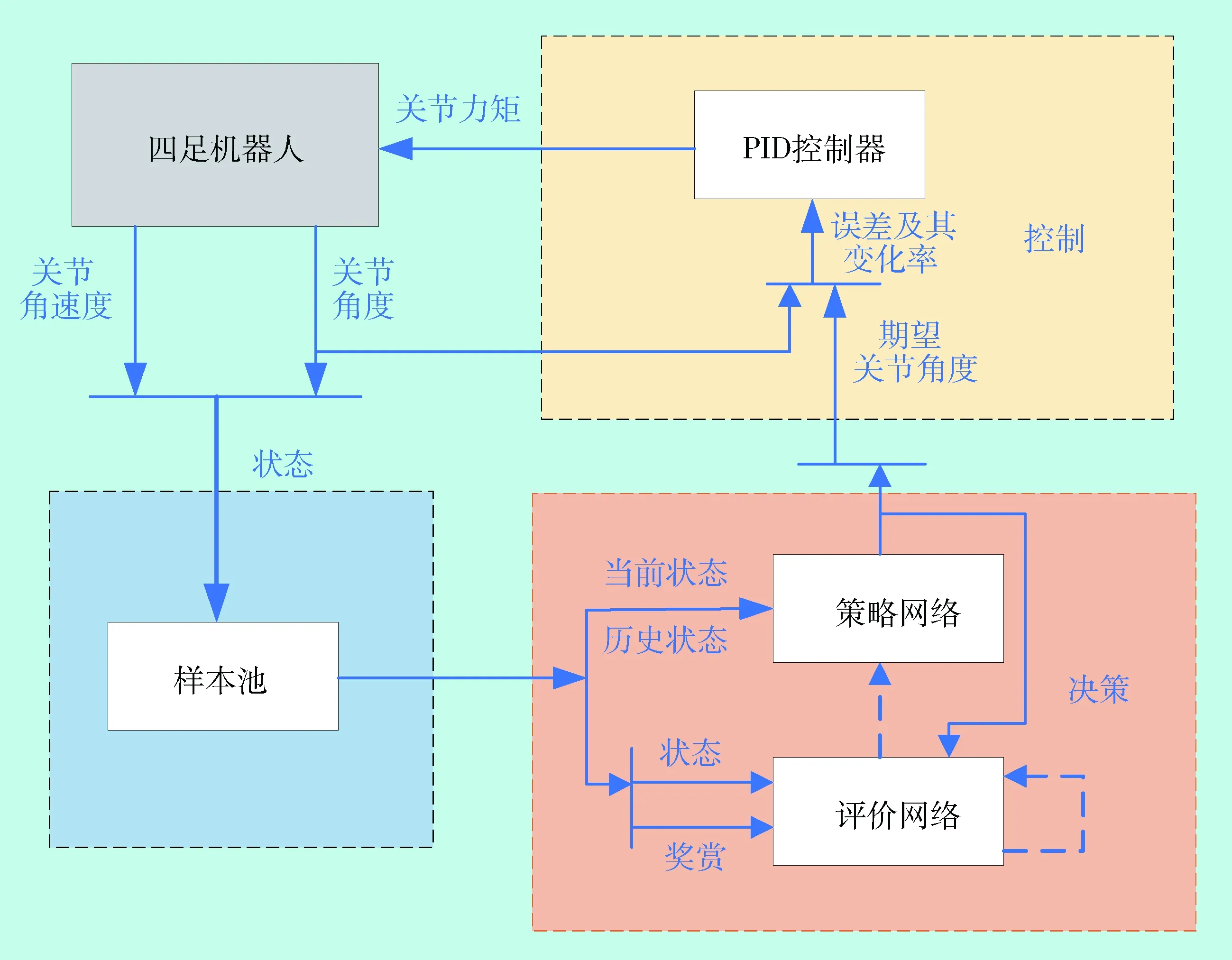
图4 四足机器人步态控制框图Fig.4 Quadruped robot gait control block diagram

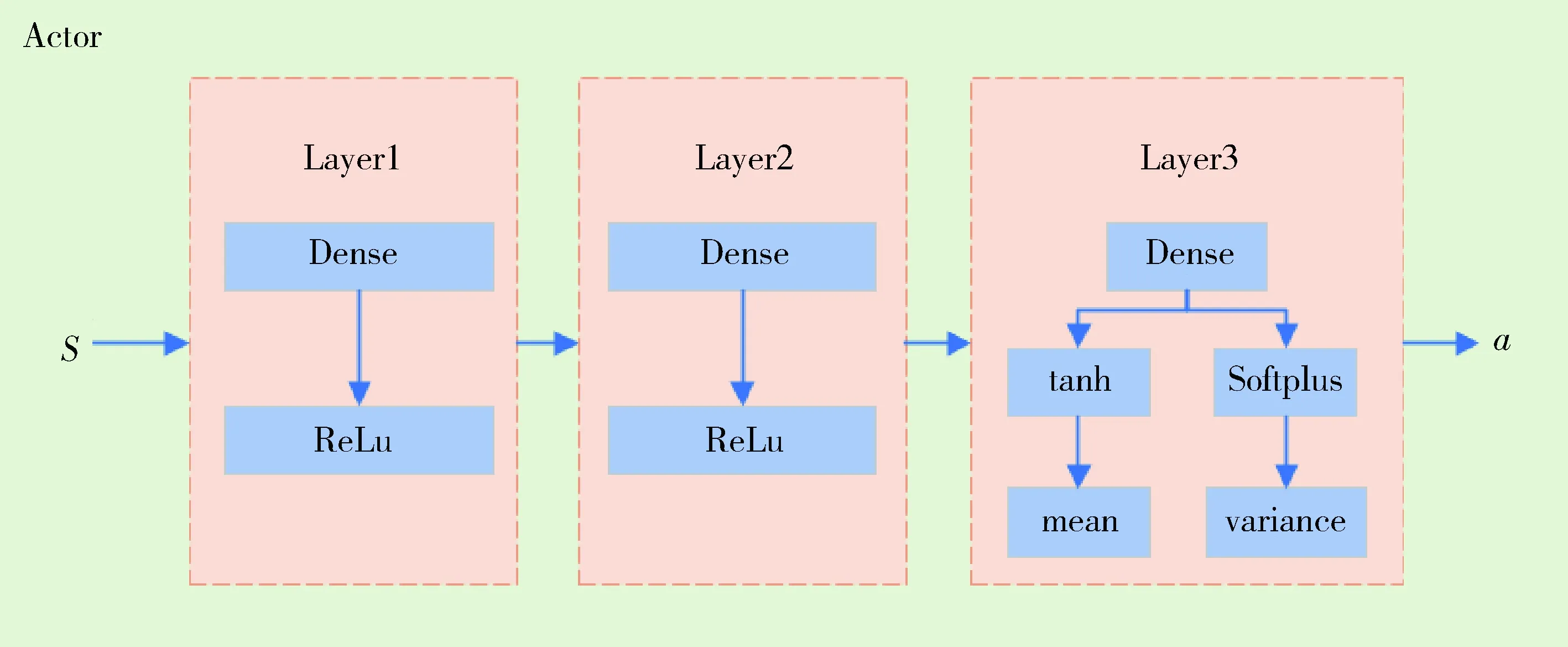
图5 PPO策略网络结构Fig.5 PPO actor network structure

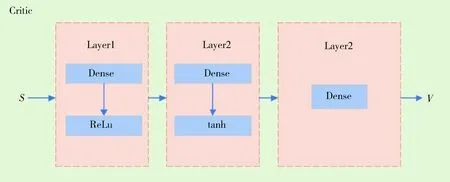
图6 PPO评价网络结构Fig.6 PPO critic network structure

图5和图6分别展示了PPO网络的策略网络和评价网络结构.策略网络设计了三个隐层，每个隐层的节点数为256，状态S输入到网络中，通过不同的激活函数最终分为均值和方差两部分，确定一个正态分布，通过采样得到动作a的值；评价网络设计了三个隐层，每个隐层有256个节点，状态S输入到网络中后输出状态值函数V.其中状态值函数V是状态S的函数，表示在当前状态下，执行当前的策略所获得的累积折扣回报.

近端策略优化(PPO)算法参数设置如表1所示.

深度确定性策略梯度算法及改进深度确定性策略梯度算法的策略网络和评价网络如图7和图8所示.策略网络设计了三个隐层，每个隐层的节点数为256，状态S输入到网络中，最终输出时会增加一个正态分布的噪声得到动作a的值，增强对环境的探索能力；评价网络设计了三个隐层，每个隐层有256个节点，状态S和动作a同时输入到网络中后输出状态动作值函数Q.状态动作值函数Q是状态S和动作a的函数，表示在当前状态下，执行当前的动作a后再执行当前的策略所获得的累积折扣回报.

表1 PPO算法参数Tab.1 PPO algorithm parameters

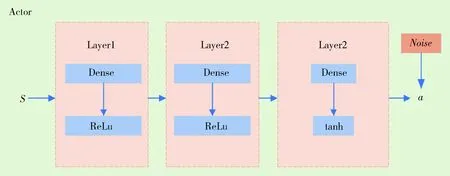
图7 DDPG策略网络结构Fig.7 DDPG actor network structure

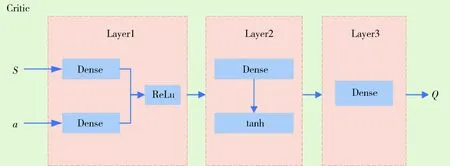
图8 DDPG评价网络结构Fig.8 DDPG critic network structure

深度确定性策略梯度(DDPG)算法网络参数设置如表2所示，其中标有*号的为使用改进DDPG算法所增加的参数取值.

本论文使用了以上三种算法对四足机器人进行训练，每回合平均回报曲线如图9所示.

从实验结果可以看出，原始的DDPG算法在复杂的任务中很难应用，在训练过程中一直处于不稳定的状态；改进的DDPG算法虽然使用优先级经验回放提高了样本利用率，但是由于不限制参数更新步长，在初始时刻更新很快，但是随着训练的进行，易于陷入局部最优，导致学不到更优的策略；PPO算法限制了策略的更新幅度，策略的更新幅度更加合理，因此获得了更好的训练效果，在实验中得到的回报稳定上升.

图3～9为三种算法的状态动作值函数的对比曲线.

表2 DDPG算法参数Tab.2 DDPG algorithm parameters

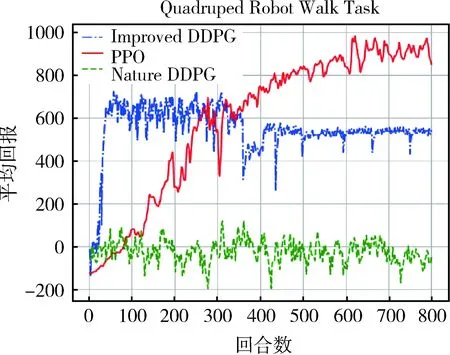
图9 四足机器人步态控制回报对比曲线Fig.9 Quadruped robot gait control return comparison curve

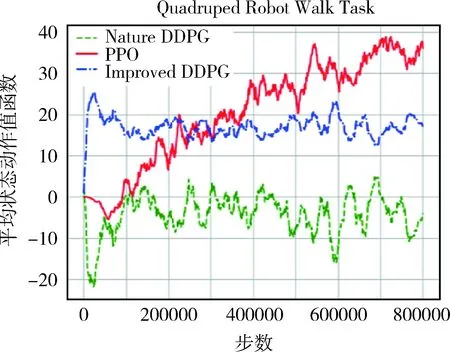
图10 四足机器人步态控制Q值对比曲线Fig.10 Quadruped robot gait control Q valuecomparison curve

通过对比可以看出，不使用优先级经验回放传统DDPG算法在训练过程中得不到很好的策略，在实际的动作选择中表现出很强的随机性；改进DDPG算法的值函数虽然有一定的提升，但是很快会收敛到局部极值；PPO算法的参数更新有策略单调不减的理论支撑，PPO算法在训练过程中表现较好，其值函数不断提高.

3 结 论

本文以四足机器人为研究对象，基于仿真环境研究近端策略优化算法在机器人控制中的应用.基于仿真平台搭建了四足机器人模型，并对机器人步态控制进行建模，将近端策略优化算法用于四足机器人步态控制中，并将实验结果与深度确定性策略梯度算法进行对比分析.实验结果表明近端策略优化算法在实际的应用中具有更好的训练效果，后续可以结合模仿学习对算法性能进一步改进.