基于终端滑模和神经网络的多目标姿态跟踪鲁棒控制*

袁长清，李政广，于海莉，左晨熠

0 引 言

随着空间技术的发展，现代航天器往往需要具备大角度机动、快速姿态跟踪等能力.此时，航天器的三轴耦合影响和陀螺效应将非常严重，这导致航天器姿态动力学方程具有很强的非线性[1].另外，由于燃料消耗、太阳帆板转动以及有效载荷运动等因素，航天器惯量参数通常会发生变化，且无法精确预知[2].因此，考虑参数不确定性和外部干扰力矩情况下，航天器多目标姿态跟踪鲁棒控制问题极具挑战性.近几年发展的终端滑模控制技术(TSMC)[3-5]，具有有限时间收敛属性，即系统在有限时间内收敛到期望状态.该技术已成功应用于机械臂控制和移动目标跟踪等任务，并在航天器姿态控制领域得到了应用[6-9].神经网络技术具有高速并行处理、非线性映射、强容错能力以及对环境噪声的鲁棒性，在处理未知非线性问题时，具有很强的优势[10-12].该技术已成功应用于空间机械臂平台、新型战机及一些复杂航天器的控制系统[13].

本文研究了航天器编队飞行多目标姿态跟踪控制问题.首先建立了多体航天器的动力学方程，然后基于径向基函数神经网络和非奇异终端滑模，设计了多目标姿态跟踪鲁棒控制器，并应用Lyapunov稳定性理论证明了系统闭环稳定性.

1 多体航天器动力学方程

本节主要建立多体航天器动力学方程.主航天器由中心刚体、刚性天线支撑臂、星载相机和快速机动天线等组成，星载相机固连于中心刚体，天线铰接于支撑臂.参考坐标系OIXIYIZI、OoXoYoZo、ObXbYbZb和OaXaYaZa分别为地心惯性系、轨道坐标系、中心体固连坐标系和天线固连坐标系，如图1如示.

考虑航天器在俯仰平面内运动的情况，应用达朗伯尔原理，可得动力学方程为

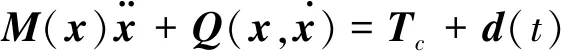
式中，M为系统总质量，ωw飞轮转速，ρC系统质心相对Ob点的距离，Jw为飞轮惯量,其他参数物理意义见表1.为了方便控制器设计，将方程等价表示成如下形式：

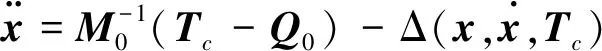
其中下标 “0”表示标称值，下标“Δ”表示模型的不确定部分和外部干扰力矩.

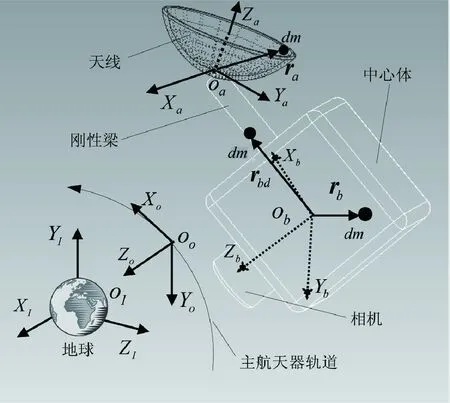
图1 多体航天器Fig.1 Multi-Body Spacecraft

2 鲁棒姿态跟踪控制器的设计

文献[6]提出的非奇异终端滑动模态(NTSM)，具有良好的有限时间收敛属性，同时避免了传统终端滑动模态的奇异问题.由文献[11]知，神经网络能以任意精度逼近高度非线性函数.考虑模型不确定性和外部干扰力矩，充分利用NTSM和神经网络的优点，设计了编队飞行多目标姿态跟踪鲁棒控制器，并对闭环系统稳定性进行分析.

2.1 鲁棒控制器设计

选取如下非奇异终端滑模[6]

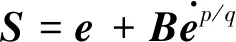
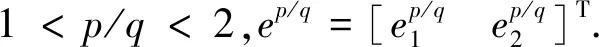
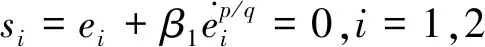
其中ei=0(i=1,2)为终端吸引子.求解方程可得抵达时间[14]

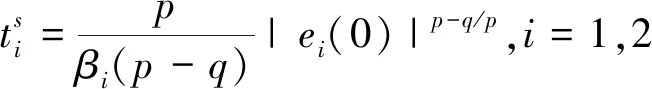
其中ei(0)(i=1,2)为初始条件.方程表明跟踪误差在有限时间内收敛到零.

考虑模型不确定性和外部干扰力矩，基于NTSM和神经网络，设计鲁棒控制器如下：

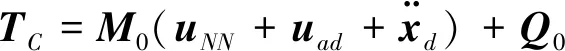
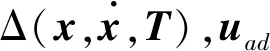
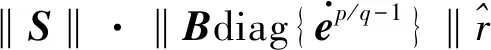
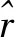
下面设计神经网络控制器uNN.选用RBF神经网络，网络的输入层、隐含层、输出层的节点数分别为ni、nk、nj.RBF神经网络可以表示为

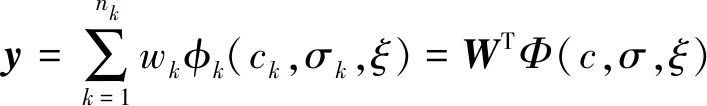
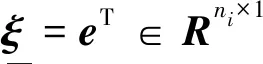
基于文献[3]的结论，式(2)中的模型误差可以由RBF神经网络来逼近

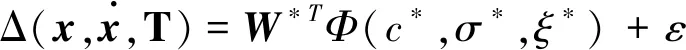
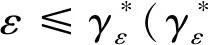
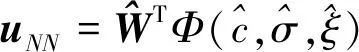
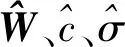
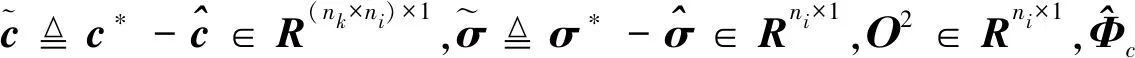
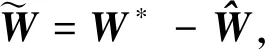
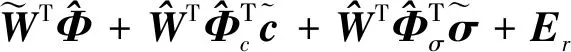
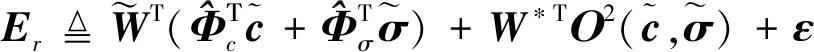
神经网经训练一般分为离线学习和在线学习两种策略.在线学习策略能使控制器具有实时学习能力和更好的鲁棒性，被广泛采用.根据实时控制需求，在线学习算法必需具有快速收敛速度.当逼近误差很小时，传统梯度下降学习算法收敛速度将会变得缓慢，影响控制性能.为了加快学习算法的收敛速度，利用NTSM有限时间收敛属性，提出一种改进的梯度下降学习算法——NTSM-OLA.

NTSM-OLA可以被描述为

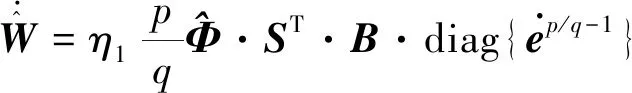
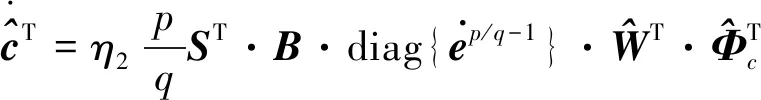
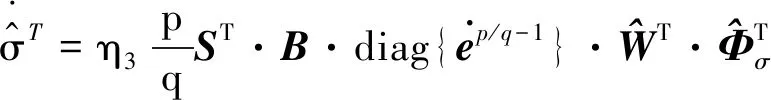
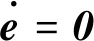
综上所述，考虑多体航天器系统，多目标姿态跟踪鲁棒控制器(6)由神经控制器(11)和自适应终端滑模控制器(7)组成，神经网络在线学习算法为式(13)、(14)和(15)，自适应学习算法由式给出，则系统跟踪误差在有限时间内收敛为零.

3.2 稳定性分析

将式(6)代入到方程(2)中，可得到系统闭环方程为：

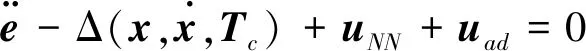
选择Lyapunov 函数如下：

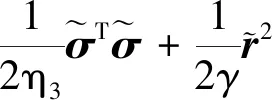
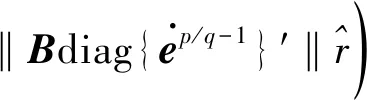
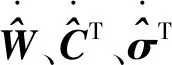
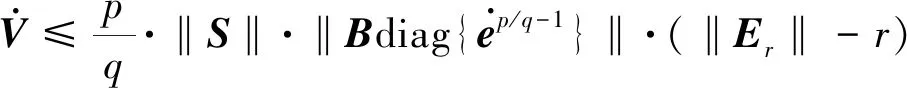
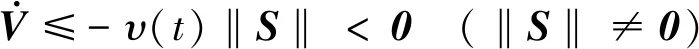
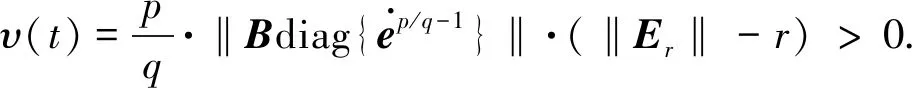
3 数值仿真

考虑存在模型不确定性和外部干扰情况下，应用所设计控制器，对航天器多目标跟踪任务进行数值仿真.航天器的物理参数如表1所示.

外部干扰力矩取为如下形式：

仿真过程中，中心体惯量按如下规律变化：当t=0 s、5 s、15 s时，中心体的惯量分别变化为标称值的90%、80%、60%.RBF神经网络隐含层神经元数目选为20个.控制器参数选择为b11=35.0，b22=35.0，p=7.0，q=5.0，γ0=0，γ=0.01，η1=1.2，η2=0.5,η3=0.5.

为了方便控制性能的比较，仿真中分别采用如下三个控制器：ISM控制器(如式(21))，NTSM控制器(如式(22)[6]和NTSM-RBFN鲁棒控制器(如式(6)).

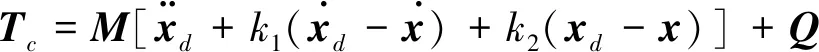
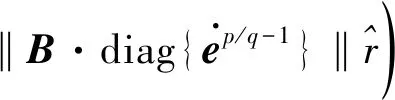
仿真结果如图2至图5所示.其中图2和图3分别为中心体和天线的姿态跟踪时间历程，图4和图5分别是中心体和天线的姿态跟踪误差.可以看出采用NTSM-RBFN鲁棒控制器时，其RBFN能够快速的补偿模型不确定部分和外部干扰力矩，且所采用的基于非奇异终端滑模的神经网络在线学习算法能够满足在线控制的实时性需求.通过上述仿真结果可知，NTSM-RBFN鲁棒控制器对模型不确定性和外部干扰具有更优越的鲁棒性能.

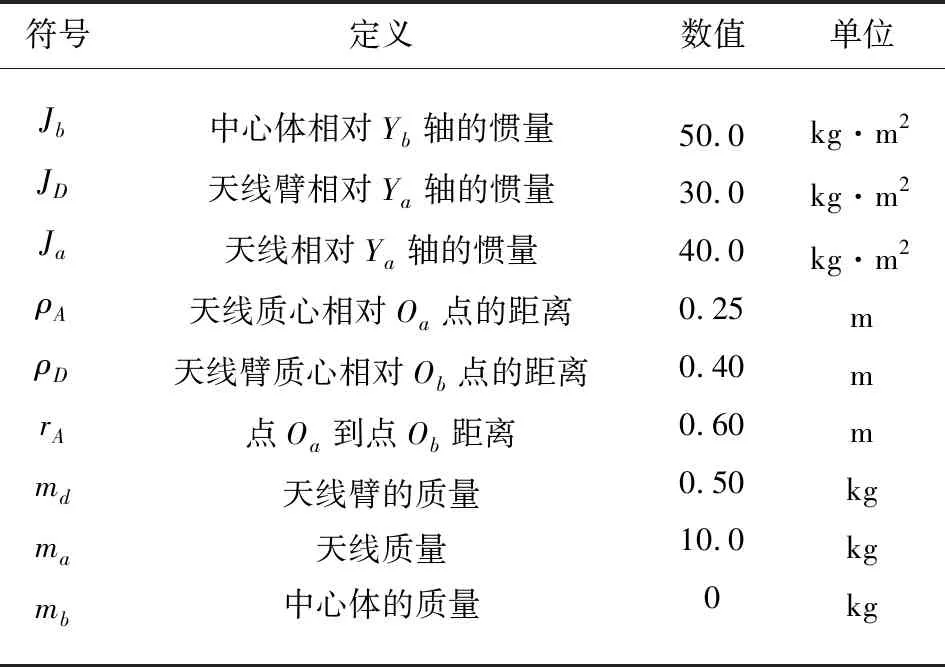
表1 航天器物理参数Tab.1 Spacecraft physical parameters

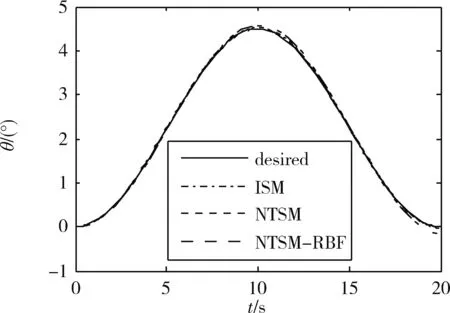
图2 中心体姿态跟踪变化曲线Fig.2 Center body attitude tracking curve

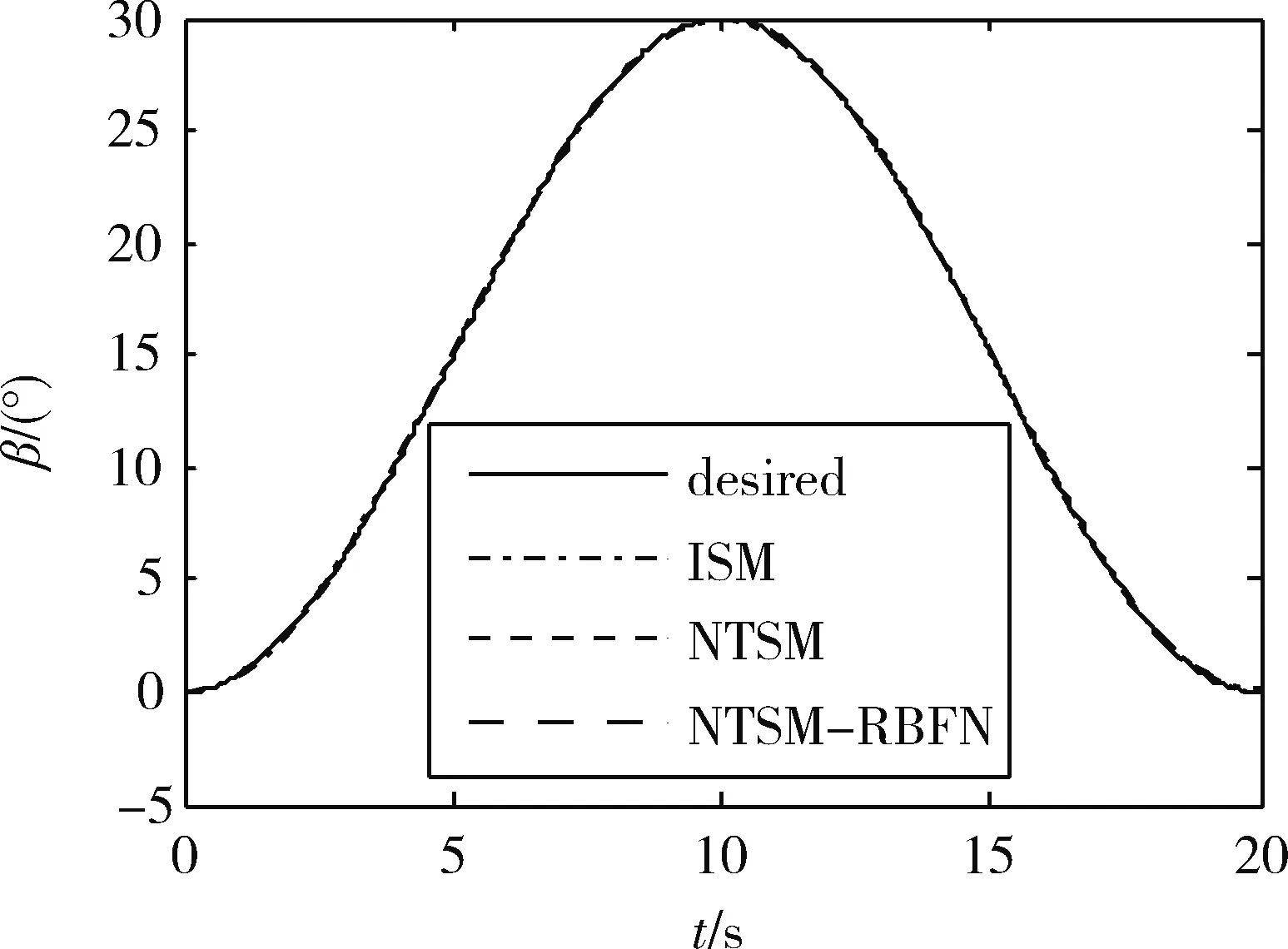
图3 天线姿态跟踪变化曲线Fig.3 Antenna attitude tracking curve

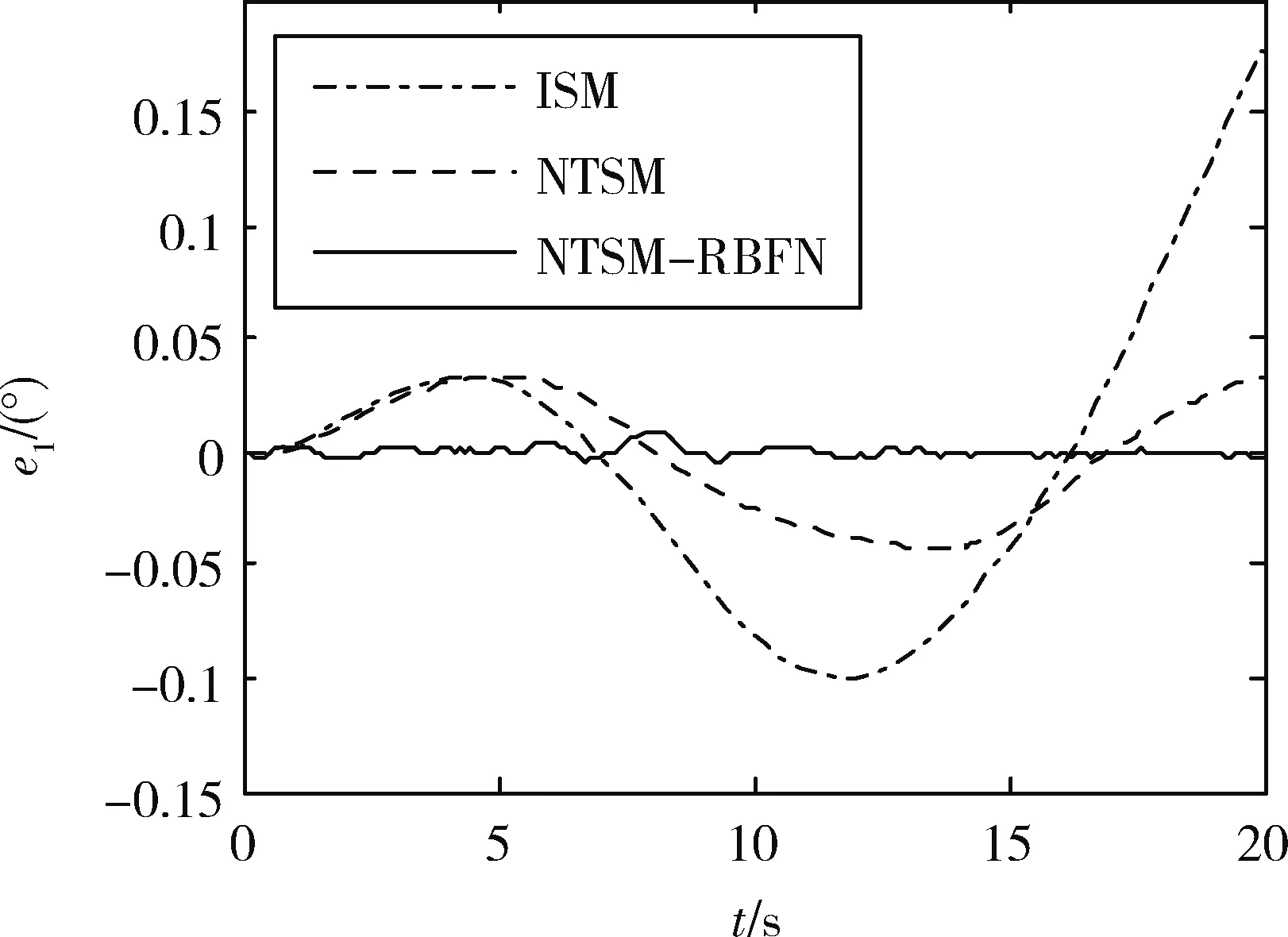
图4 中心体姿态跟踪误差Fig.4 Center body attitude tracking error

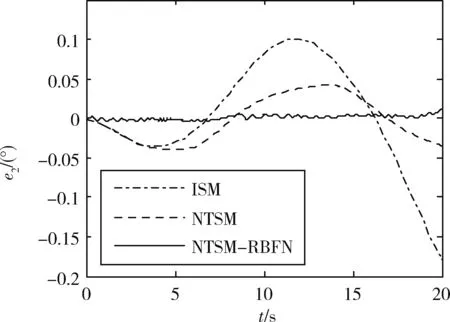
图5 天线姿态跟踪误差Fig.5 Antenna attitude tracking error

4 结 论

本文基于径向基函数神经网络和非奇异终端滑模技术，提出了一种航天器编队飞行多目标姿态跟踪鲁棒控制器.该控制器由径向基函数神经网络和自适应控制器组成.前者用于补偿模型不确定部分和外部干扰，后者用于补偿神经网络的逼近误差和实现期望的控制性能.基于非奇异终端滑模的有限时间收敛属性，提出了一种神经网络在线学习算法，有效提高了神经网络的逼近性能.应用Lyapunov稳定理论，证明了系统的闭环稳定性.数值仿真证明了所设计控制器具有优越跟踪性能，并对模型不确定和外部干扰具有良好鲁棒性.