挠性卫星姿态的有限时间终端滑模稳定控制

常雅杰,赵 晨，段传辉

0 引 言

随着航天科技的迅猛发展，卫星结构的大型化和复杂化已经是当今这个航天任务多样化的时代不可避免的发展趋势.为在延长卫星在轨寿命的同时高效完成任务需求，各类功能附件的安装十分必要.卫星在轨运行时，附件结构受环境干扰产生的振动响应以及挠性附件与卫星本体之间的动力学强耦合效应一直以来都是挠性卫星姿态稳定控制中亟待解决的问题.

近年来，在挠性卫星的姿态控制方面，现代控制理论研究成果受到了越来越多的关注，鲁棒控制[1-2]、自抗扰控制[3]、预测控制[4-5]、最优控制[6-7]等控制方法得到了广泛的应用，例如文献[8]针对CNES微小挠性卫星TARANIS具有的转动惯量、固有频率及阻尼存在不确定性的情况，基于LMI方法使用S函数设计了增益可调的鲁棒自适应控制器；WU等[9]针对安装有大型挠性附件和有效载荷的航天器高精度姿态控制问题，首先建立了拉格朗日形式的姿态动力学模型，然后针对在轨航天器受到的干扰设计了基于LMI的H∞输出反馈控制器，并采用凸优化算法处理模型的不确定性；文献[10]将挠性航天器受到的外干扰和执行机构约束考虑在内，基于Sontag型公式和Lyapunov方法设计了一种新型鲁棒逆最优控制策略实现姿态的机动控制; 文献[11]针对无角速度敏感器的挠性卫星提出了一种将ADRC和输入成型技术相融合的新型控制方案，采用机动路径规划与输入成型相结合的过渡过程削弱振动响应，设计ESO估计干扰和姿态角速度信息，并引入了非线性反馈控制律实现期望姿态跟踪和实时干扰补偿.如上所述，有大量的控制方法可以实现卫星姿态的收敛，然而对于控制系统而言，有限时间收敛与现有控制方法的渐近收敛特性相比，往往意味着更好的控制性能和鲁棒性，而采用连续状态反馈的终端滑模方法就是一种性能优良的有限时间控制方法[12-13].但其中很大一部分文献忽略或简化了卫星的刚柔耦合效应，并简单的将外干扰力矩设为零或常值，而忽视了卫星在轨运行的真实特性.

因此，致力于实现挠性卫星的有限时间姿态稳定控制，并充分考虑卫星在轨运行时的真实特性，本文提出了一种基于双幂次趋近律的终端滑模控制器，并通过两种不同类型的观测器将外干扰力矩和刚柔耦合效应考虑在内.论文结构如下所述：第1节建立了挠性卫星的数学模型；第2节构造了非线性干扰观测器、超螺旋观测器和终端滑模控制器，并采用Lyapunov理论证明了闭环控制系统的稳定性；最后，在第3节通过仿真验证了所提控制算法的有效性.

1 挠性卫星的数学模型

1.1 姿态运动学模型

基于四元数描述的卫星姿态运动学方程如下[14]：

1.2 姿态动力学方程

考虑在姿态控制过程中，帆板相对于卫星主体无转动的情况，采用混合坐标建立挠性卫星的姿态动力学模型[14]：

根据卫星的动力学方程可以很明显的看出，卫星本体的角速度影响帆板附件的挠性模态，相应的，帆板模态的振动响应也对卫星姿态产生影响.

2 挠性卫星有限时间姿态控制器设计

将卫星运行过程中受到的外干扰力矩和刚柔耦合效应考虑在内，本文结合两种不同的观测器设计了终端滑模控制器实现挠性卫星的有限时间姿态稳定控制.

2.1 非线性干扰观测器设计

在卫星的动力学模型(2)中存在未知的外界干扰Td,为了提高挠性卫星控制系统的控制精度，基于物理意义明确、工程实现便捷的考虑，本文设计了非线性干扰观测器来逼近不确定系统(2)中的未知干扰，从而补偿干扰给系统带来的影响，提高系统的控制性能.

J-1Tc+J-1Td(3)

可以得到状态空间方程如下：

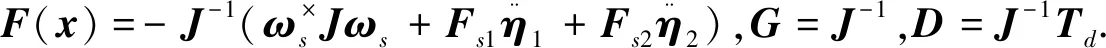
针对系统(4)可以设计如下形式的NDO：

根据式(5)及卫星动力学方程(2)可以得到如下表达式

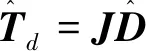
为证明干扰估计的有效性，定义Lyapunov函数

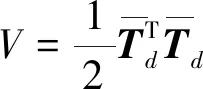
对式(7)求导得

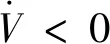
2.2 超螺旋观测器设计

引理1[16].考虑系统

设计超螺旋观测器形式如下：

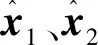
2.3 终端滑模控制器设计

首先假设期望的姿态四元数为qd,则姿态的误差四元数可以定义为

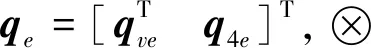
其次，假设期望的姿态角速度为ωd,则姿态的误差角速度可以定义为

ωe=ωs-ωr(13)

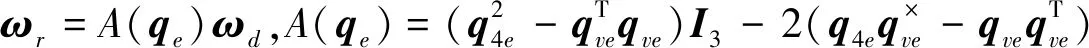
根据式(11)～式(14)，可以由运动学和动力学方程(1)、(2)获得挠性卫星的姿态误差方程如下：

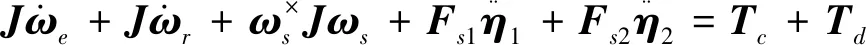
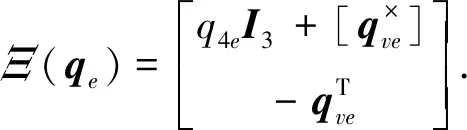
s=x2+α0sigχ0(x1)(16)

其中：α0>0，χ0∈(0,1)，sigχ0(x)=|x|χ0sgn(x). 由于“抖振”现象是传统滑模控制中的一个显著缺点，容易对控制系统的稳定性产生威胁，因此，为同时实现削弱系统抖振和提高状态远离滑模面时的运动速度，采用如下形式的双幂次趋近律：

其中：α>1,0<β<1,k1>0,k2>0.

采用上述趋近律时，在滑模面附近，k1sigα(s)项可以忽略，则由0<β<1可知，趋近滑动模态的速度逐渐减小，抖振现象有所削减；在远离滑模面时，k2sigβ(s)项可以忽略，则由α>1可知，趋近滑动模态的速度显著加快，减小了运动时间.

为了同时实现系统状态到达滑模面和在滑模面上趋近零平衡点的有限时间特性，本文选取如下形式的控制律：

Tc=ueq+ureach(18)

其中，ueq为等效控制律.

式(18)中的第二项主要在到达阶段发生作用，用于确保系统状态在到达阶段的有限时间特性.控制律的形式如下：

ureach=-J[k1sigα(s)+k2sigβ(s)](21)

因此，本文设计的挠性卫星终端滑模控制律形式如下：

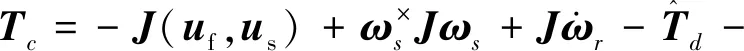
引理2[17].考虑系统

(1)V是正定函数

(2) 存在k1>0,00且为常值时，如果V满足下列任一微分不等式

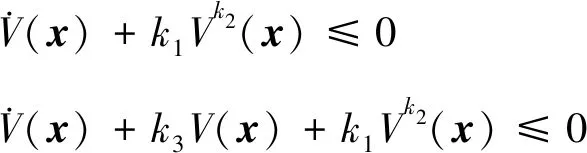
则系统(23)是有限时间稳定的.

定理1.对系统(15)采用控制律(22)可使得卫星姿态在有限时间内趋于平衡点.

(1) 当系统状态(x1,x2)位于A区域时，式(22)中的饱和函数取为

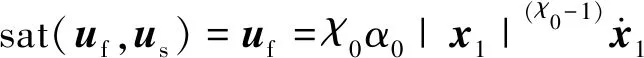
因此可将控制律改写为

定义Lyapunov函数

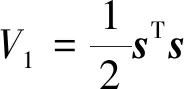
对其求导得

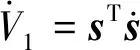
根据引理2可知，系统(15)将在有限时间内到达滑模面(16).

图1 状态空间的区域划分示意图Fig.1 Regional division of state space

(2) 当系统状态(x1,x2)位于B区域时，式(22)中的饱和函数取为

sat(uf,us)=us(30)

则可以将控制律(22)改写为

J[k1sigα(s)+k2sigβ(s)](31)

则有

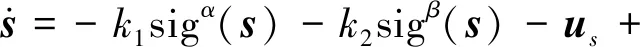
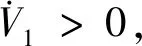
因此在区域B上总有以下情况成立：

根据式(15)可知，状态x1(t)的解可以表示为

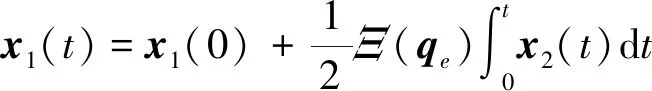
则根据图1可知，在区域B内，当x2(t)>0时，x1(t)单调递增直到穿越区域B和区域A的边界；当x2(t)<0时，x1(t)单调递减直到穿越区域B和区域A的边界.因此可知，状态(x1,x2)不会始终保持在区域B内，而是会在有限时间内从区域B穿越到区域A.一旦状态(x1,x2)到达区域A,系统将满足s有限时间稳定条件.

最后，当系统到达滑模面s=0以后，定义Lyapunov函数

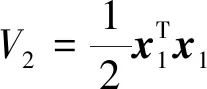
对其求导得

根据引理2可知，系统(15)的状态将在有限时间收敛到(0,0).

证明完毕.

3 仿真结果与分析

为了验证本文提出的控制器的控制效果，本节对带有两副太阳帆板的挠性卫星进行仿真分析，并与采用一般滑模控制方法的仿真结果进行对比.

用于对比的滑模控制律如下：

u=-K1s-D1F(s)+ueq(38)

式中K1=diag{ki}，D1=diag{di}，ki>0，di>0，i=1,2,3,F(s)={sgn(s1),sgn(s2),sgn(s3)}T.

滑模控制器采用的切换函数为

s=ωe+kqve(39)

(1) 卫星本体相关参数的取值如表1所示.

(2) 定义Ci=2εΩ，Ki=Ω2(i=1,2),相关参数取值如表2所示.

(3) 仿真过程中选取控制参数如表3所示.

表1 卫星本体相关参数Tab.1 Parameters of the satellite body

表2 太阳帆板前六阶振型频率与阻尼比Tab.2 Parameters of solar panel

表3 仿真过程控制参数Tab.3 Parameters of observer and controller

首先，为了验证本文提出的非线性干扰观测器(5)对环境干扰力矩的估计效果，给出环境干扰力矩观测误差曲线如下图2所示.

图2 环境干扰力矩观测误差曲线Fig.2 Response of observing error of disturbance torque

根据图2可知，仿真施加的环境干扰力矩与非线性干扰观测器估计的干扰力矩误差收敛迅速，100 s内误差收敛到0附近，400 s后稳态观测误差达到2.3×10-4N·m数量级，说明本文提出的非线性干扰观测器对环境干扰力矩具有良好的观测效果.

下面首先给出一般滑模控制器(38)的仿真结果.图3～图6给出了采用一般滑模控制器对卫星姿态稳定控制的仿真结果，根据图3和图4可知，卫星姿态四元数误差及姿态角速度误差曲线在50 s后收敛到5×10-3数量级，但“抖振”现象剧烈，卫星姿态稳定控制的误差在平衡点附近产生了振荡，卫星姿态角速度误差最大达到0.27(°)/s，且姿态角速度误差在370s后才收敛到1×10-5数量级.图5和图6给出了挠性帆板的6阶模态振动响应，可以看出在50 s后两块帆板的振动幅值均收敛到1×10-4数量级，但是模态坐标曲线波动剧烈.图7～图10给出了本文所提终端滑模控制器对卫星姿态稳定控制的仿真结果，根据图7和图8可以看出，虽然仍旧存在“抖振”现象，但姿态角速度误差最大值仅为-0.025(°)/s，且卫星姿态四元数误差及姿态角速度误差曲线在50 s后分别收敛到6.5×10-3和1×10-5数量级；图9及图10给出了卫星+Y及-Y方向挠性太阳帆板的6阶模态振动响应，从图中可以看出，模态坐标收敛迅速，在50 s后两块帆板的振动幅值均收敛到5×10-5数量级.从上述变化曲线及数据分析可以看出，本文提出的终端滑模控制器较一般控制器而言具有良好的收敛速度、控制精度和稳定度，在有效抑制挠性帆板结构振动响应的同时实现了卫星姿态的高精度高稳定度控制.

图3 姿态四元数误差曲线Fig.3 Response of quaternion error

图4 姿态角速度误差曲线Fig.4 Response of attitude angular velocity error

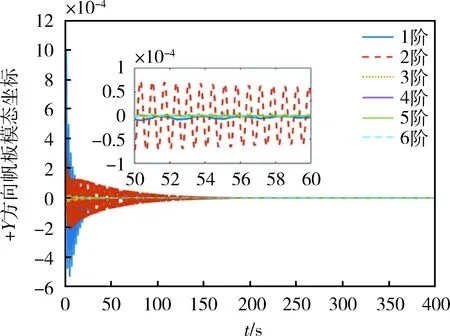
图5 +Y方向帆板模态坐标曲线Fig.5 Response of vibration modes in +Y

图6 -Y方向帆板模态坐标曲线Fig.6 Response of vibration modes in -Y

图7 姿态四元数误差曲线Fig.7 Response of quaternion error

图8 姿态角速度误差曲线Fig.8 Response of attitude angular velocity error

图9 +Y方向帆板模态坐标曲线Fig.9 Response of vibration modes in +Y

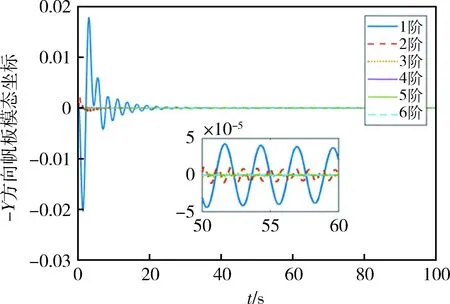
图10 -Y方向帆板模态坐标曲线Fig.10 Response of vibration modes in -Y

4 结 论

本文针对存在外部干扰和刚柔耦合效应的挠性卫星，采用观测器估计未知信息，提出了一种终端滑模有限时间控制方法，该控制方法具有以下优点：

(1) 通过非线性干扰观测器和超螺旋观测器估计了外部干扰力矩和卫星角加速度信息；

(2) 采用双幂次趋近律实现了在削弱系统抖振的同时提高状态远离滑模面时的运动速度；

(3) 通过Lyapunov理论证明和数据仿真分析验证了该方法在有效抑制挠性振动的同时可以快速、高效的实现卫星姿态的有限时间稳定.