在模型化思想下用角度关系处理立体几何问题
余亮


高中立体几何的基础是点、线、面位置关系和空间几何体结构.立体几何中外接球、异面直线夹角等问题常常通过将几何体补全成长方体、平行六面体、“三节棍”等模型来解决.反之,我们也能从长方体、平行六面体等模型中一部分来得到角的数量等价关系,再通过模型化思想和角的等价关系式来解决立体几何中角的问题.首先给出两个引例.
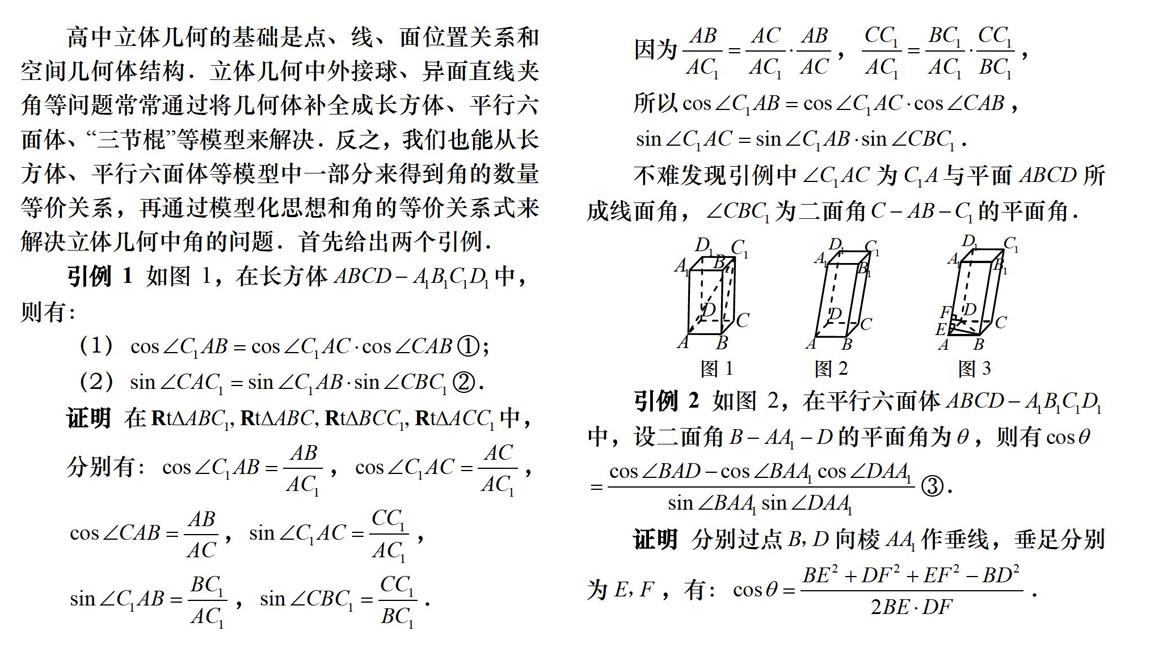
引例1如图l,在长方体ABCD-A1B1C1D1中,则有:
(1)cos∠C1AB=cos∠C1AC·cos∠CAB①;
(2) sin∠CAC1=sin∠CiAB·sin∠CBC1②.
证明在Rt△ABC1,Rt△ABC,Rt△BCC1,Rt△ACC1中,
所以cos∠C1AB=cos∠C1AC·cos∠CAB,
sin∠C1AC=sin∠C1AB·sin∠CBC1.
不难发现引例中∠C1AC为C1A与平面ABCD所成线面角,∠CBC1为二面角C-AB-C1的平面角.
引例2 如图2,在平行六面体ABCD-A1B1C1D1中,设二面角B-AA1-D的平面角为θ,则有cosθ
证明 分别过点B,D向棱AA1作垂线,垂足分别
引例l和引例2的三个结论为相关问题的解决提供了模型化的结论,以下例说之.
例1 (2017年高考全国III卷理.16)a,b为空间中两条互相垂直的直线,等腰直角三角形ABC的直角边AC所在直线与a,6都垂直,斜边AB以直线AC为旋转轴旋转,有下列结论:
①当直线AB与a成60°角时,AB与6成30。角;
②当直线AB与a成60°角时,AB与b成60°角;
③直线AB与a所成角的最小值为45°;
④直线AB与a所成角的最小值为60°.
其中正确的是_________.(填写所有正确结论的编号)
解析 平移直线a,b为相交直线,并交于点B,则构造成长方体(一部分)(如图所示),设AB与a所成角为θl,AB与b所成角为θ2·
由结论①得cosθi=cos∠ABC·cos∠CBM,
cosθ2=cos∠ABC·cos∠CBN,
评注 (l)空间直线位置关系问题通过补形,将无形化为有形,借助长方体或平行六面体处理直线位置关系极为直观、方便;
(2)结论①描述的本质是三余弦定理:平面口的一条斜线/与a所成角为θl,a内的直线m与/在a上的射影/'夹角为θ2,/与m所成角为θ,则cosθ=cOsθl·COSθ2;
(3)由线面角的定义(最小角定理),易得直
例2 (2017年高考全国I卷理.18)如图5,在四棱锥P-ABCD中,AB//CD,且∠BAP=∠CDP=90°.
(I)略;
(Ⅱ)若PA=PD=AB DC,∠APD=90°,求二面角A-PB-C的余弦值.
(Ⅱ)解以BA,BP,BC为边构造平行六面体(如图所示),不难得到△PAB为等腰直角三形,△PBC为等边三角形;底面四边形ABCD为矩形,
则∠PBA=45°,∠PBC=60°,∠ABC=90°;
设二面角由A-BP-C平面角为θ,
由结论③有cosθ
评注 (l)长方体与平行六面体构造方式一样,都是以三边来构造四棱柱;
(2)结论③描述的本质是三面角三余弦定理:三面角中任一二面角的余弦值,等于其所对面角的余弦减去另两个面角的余弦之积,再除以这两个面角的正弦之积.
例4 (2017年高考全国II卷理.19)如图7,四棱锥P-ABCD中,侧面PAD为等边三角形且垂直90°,E是PD的中点.
(I)略;(Ⅱ)点M在棱PC上,且直线BM与底面ABCD所成角为45°,求二面角M-AB-D的余弦值.
解 以BM为长方体体对角线,BC为长方体一条棱,CM为长方体一条面对角线,AB为长方体一条棱所在直线构造长方体.过程如下:取AD边上中点O,连接PO,CO;再过点M作PO的平行线MD1交CO于点Dl;再过点D1作BC的平行线交AB于点A1(如图8),以D1C,D1M,D1A1构造长方体A1BCD1-M1N1NM(如图9)由结论②不难得到,∠MA1D1为二面角M-AB-D的平面角.
因为BM与底面ABCD所成角为45°,
则sin45°=sin∠MA1D1·sin∠MBA1.
评注 (l)对于模型化思想,引例不仅仅提供了角与角关系,更提供了得到线面角、二面角的方法.
(2)结论②描述的本质是三正弦定理:二面角M-AB-N的度数为a,在平面M上有一条射线AC,它和棱AB所成角为β,和平面Ⅳ所成的角为y,则siny=sina·sinβ.
參考文献
[1]王强芳.立体几何问题的模型化处理[J].中学数学教学参考,2006 (07):17-19

