带有多未知性的无人车编队控制

王晓森， 曹国华

(长春理工大学 机电工程学院长春 130022)

近二十年来,多智能体系统的分布式控制得到了学者的极大关注[1-5],现已广泛用于智能电网,移动传感器网络,无人车编队等领域[6-8].编队控制作为分布式控制的典型问题得到了控制学者的广泛关注[9-12], 它意味着利用局部信息设计分布式控制协议使得智能体能够收敛到指定的几何队形.由于多智能体系统不可避免受到未知参数,外部干扰等因素的影响,因此文献[10-12]分别利用滑模方法,自适应方法和内模原理解决了带有未知参数和干扰的多智能体系统分布式编队控制问题.

非完整无人小车是一种典型的非线性系统,它在原点处的线性化系统是不可控的但其本身是可控的[13],从而导致反馈可线性化技术不再适用,需设计本质非线性的控制器.为控制多个小车的编队问题,文献[14-15]通过设计非线性分布式控制协议,研究了其跟踪控制问题，但值得注意的是文献[14-15]需要已知的期望轨迹.

文中致力于研究具有多未知性的非完整无人车编队控制问题.多未知性主要表现在领导者的线速度、角速度及其上界是未知的，这使得已有方法不再适用.为补偿这些未知性,文章设计了时变反馈控制协议，从而在该协议下实现了系统的编队.

1 建模与问题描述

考虑由N个具有相同结构的无人车组成的系统，第i个无人车模型如图1所示.

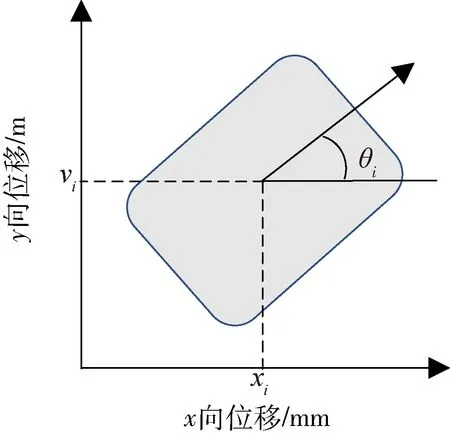
图1 无人车模型

根据文献[16]，其动力学方程为

(1)

式中：(xi,yi)是第i个小车的位置;ωi和vi分别是第i个小车的角速度和线速度.

令qi=[xi，yi，θi]T，则(1)可以写成如下矩阵形式:

(2)

无人车之间的通信图用一个有向权重图G=(V，ε，A)表示，其中V={1，…，N}表示图的节点集，ε⊆V×V表示图的有向边集，A=[aij]表示权重矩阵.在有向图G中, (i，j)表示节点i的信息流向节点j,而反过来不行.若边(i，j)∈E,则节点i称为节点j的一个邻居.

设最终由N个无人车构成的几何队形为F,每一个无人车的正交坐标为(pix,piy)且满足

(3)

其中(p0x,p0y)是几何队形F的中心坐标.不失一般性,设p0x=0,且p0y=0.

文中的控制目标是设计控制输入vi和ωi使得:

(1)所有的无人车收敛到期望的几何队形F;

(2)每一个无人车的角度收敛到期望的角度θ0;

(3)队形的中心收敛到期望的轨迹(x0(t)，y0(t)).

即，控制目标满足下式

(4)

所期望几何队形中心轨迹(x0(t)，y0(t))和期望角度θ0(t)可以看成虚拟领导者的坐标和角度且满足

(5)

为叙述方便,我们将N个无人车称为跟随者.令bi表示无人车i和虚拟领导者的通信关系且B=diag[b1,…,bn].若无人车i能够接受虚拟领导者的信息,则bi>0;否则bi=0.

为解决上述控制目标,我们给出如下假设.

假设1对每一个无人车,θi是有界的且ωi是一致激励的.

假设2系统存在多种未知性,即v0,ω0上界未知.

假设3至少存在一个跟随者能够获得领导者的信息.

2 分布式控制协议设计

定义如下变换：

(6)

其中u1i和u2i是控制输入且k0>0.对上述式子微分得到:

(7)

由式(6)和(7)可知,控制目标(4)变为

(8)

根据文献[17]可知,若(8)满足,则N个无人车能够收敛到几何队形F,即(4)满足.值得注意的是上述变换将无人车的编队问题变为一致性问题.为此,我们给出如下的分布式时变控制器：

(9)

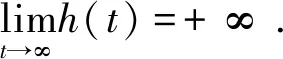
将控制器(9)代入系统(7)可得

(10)

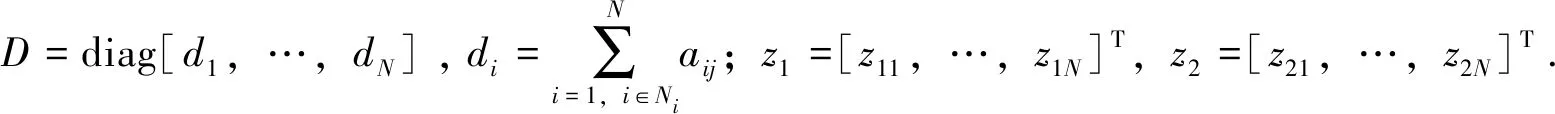
(11)

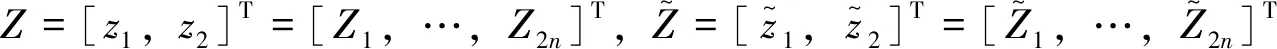
(12)

其中M=diag{L+B，L+B}.

由于符号函数是可测的且局部必然有界的,因此方程(12)的Filippov解存在,从而可以写成如下微分包含形式：

(13)

推理1 若通信图G是连通的且假设3满足，则系统(7)在分布式控制协议(9)下存在有限时间T满足

且

证:考虑如下Lypunov候选函数

则有

其中

.

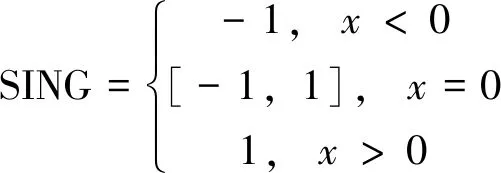
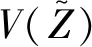
(14)

此外,由函数h(t)的性质可知,存在一个充分大的时间T1和正常数k1使得

h(t)-k>k1，t∈[T1,∞)

.

,

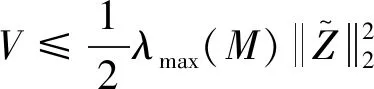
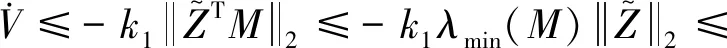
(15)

式中：λmax(M)和λmin(M)分别表示矩阵的最大特征值和最小特征值.

从上式得

因此，当

时，V(t)=0.进而可以得到z1i，z2i在有限时间内趋于z10，z20.再由分布式控制协议(9)可知u1i在有限时间内收敛到u10.

推理2 若通信图G是连通的且假设3满足,则z3i在分布式控制协议(9)下指数收敛到z30.

证:根据文献[17]中定理3.3的证明,可类似得到相应结论,故在这里省略证明.

注1:由定理1和2可知控制目标(8)满足,根据文献[17]可知N个无人车能够收敛到几何队形F,即(4)满足.

3 数值仿真

在本节中,我们通过设计一个数值仿真算例来验证所提出的控制算法的有效性.考虑一个由3个跟随者(记为1-3)和1个虚拟领导者(记为0)组成的多无人车系统，其通信关系如图2所示.

图2 三个跟随者和一个领导者组成的通信图

简便起见,若跟随者i能够接收跟随者j的信息,则aij=1；若跟随者i能够接收虚拟领导者的信息,则bi=1.期望的几何队形为(p1x，p1y)=(0，2)，(p1x，p1y)=(-2，-1)，(p1x，p1y)=(2，-1).虚拟领导者的参考轨迹可以选为x0=9sint/3,y0=9cost/3.选增益参数α=1,且增益函数h(t)=1+t.令初始条件[z1i(0),z2i(0)，z3i(0)]=[1，2，3].则我们可以得到图3-5.从图3-5可以看出(8)满足,即实现了系统的编队控制.

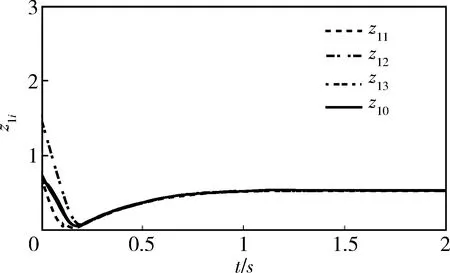
图3 状态z1i，i=0，1,2，3

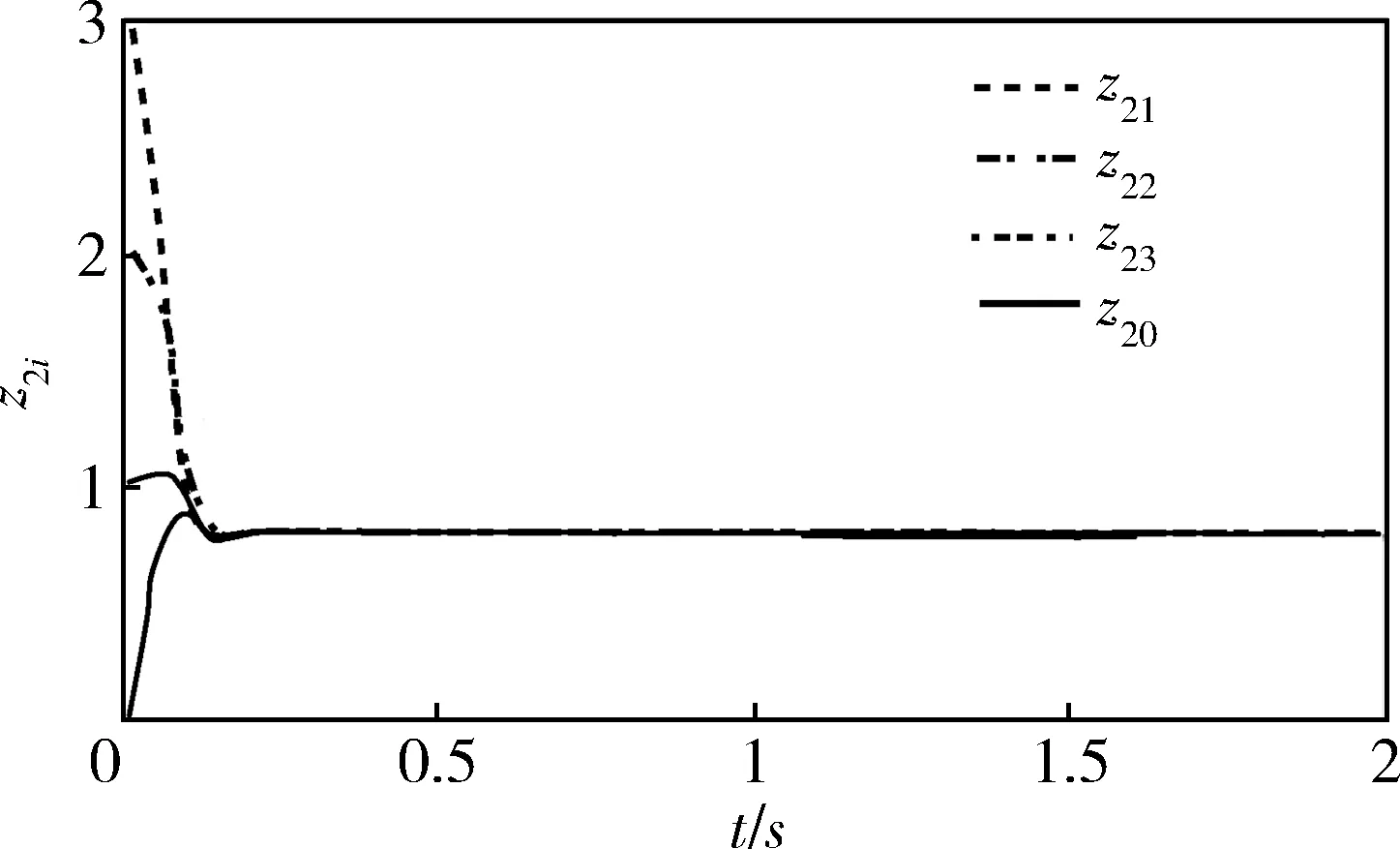
图4 状态z2i，i=0，1,2，3

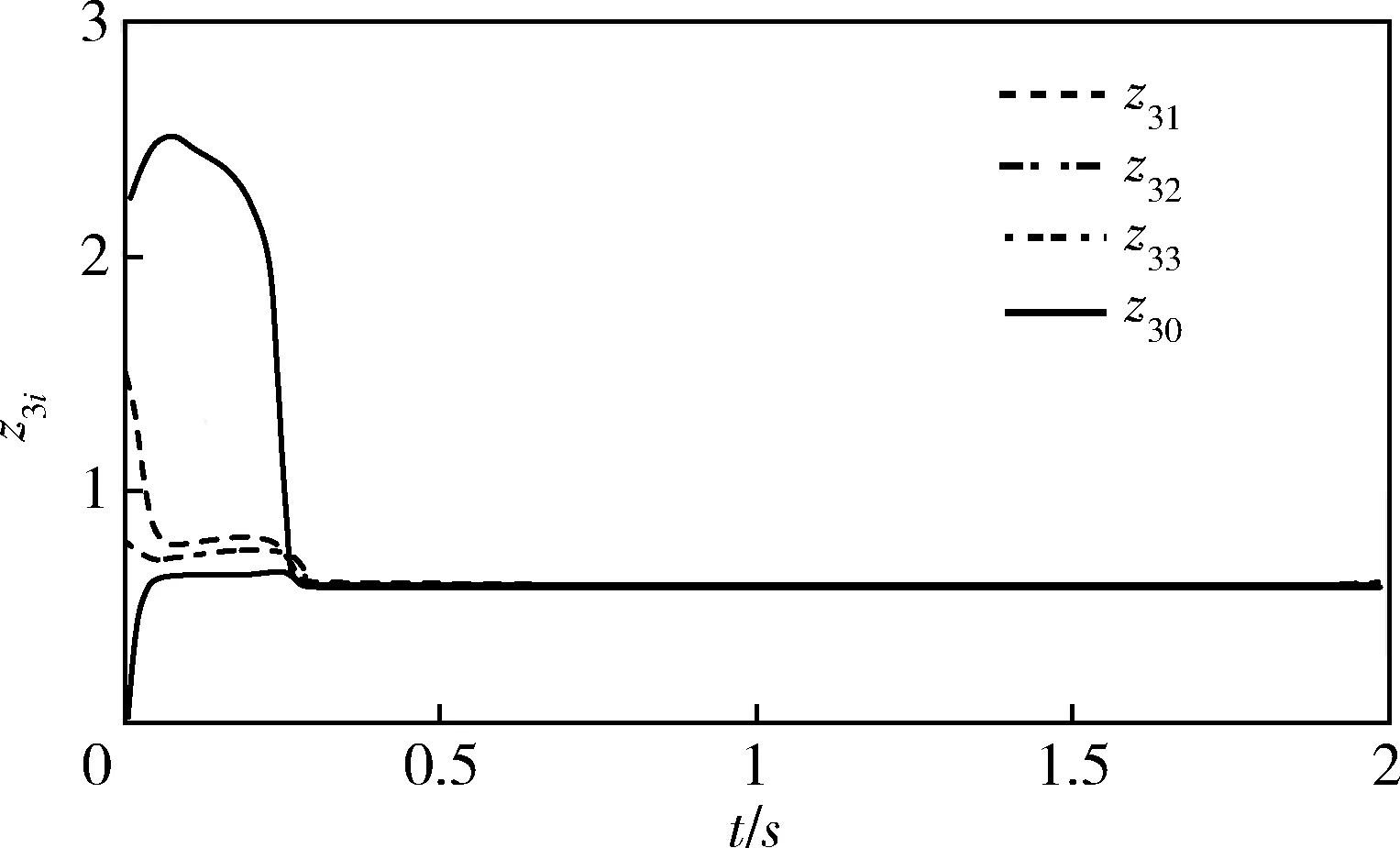
图5 状态z3i，i=0，1,2，3

4 结 论

文中主要针对无人车领导者带有未知线速度、角速度及其未知上界等多种未知性的无人车系统，解决了其编队控制问题.首先通过一个变换将无人车编队问题转化为一致性问题.然后,针对带有多未知性的无人车一致性问题,设计了时变反馈控制策略，有效地补偿了系统中存在的多种未知性.该时变策略的核心是在控制器中引入一个合适的纯时间函数使得随着时间的增加，未知性能够被补偿.最后，我们通过数值仿真算例验证了控制算法的有效性.