一种改进的汽车安全状态判断方法

时 利， 张一营, 张锐陈， 李印祥， 曾 伟， 徐春梅

(1.江淮汽车技术中心，合肥230091；2.合肥工业大学 汽车与交通工程学院，合肥230009)

随着智能汽车和智能交通的发展，汽车主动避障系统也成为了国内外研究热点.目前汽车安全距离模型大致可以分为3种.

第1种是基于制动过程运动学分析的安全距离模型[1-2],这种模型假设前方障碍物是静止的，是以自车停车后车头刚好抵达后车车尾为条件的，即停车距离为零.第2种是基于车头时距的安全距离模型[3-4],这种模型没有考虑前车运动状态的影响，当两车相对速度较大的时，不能确保行车的安全性.第3种是基于驾驶员预瞄的安全距离模型[5-6]，这种方法所建立的安全距离模型，具有强烈的主观特性，会因为驾驶员的不同而具有较大差异.

综上所述，目前已有的汽车安全状态判断方法存在以下不足：1)目前的安全距离模型没有考虑路面附着条件的限制，在低附着路面上轮胎所能提供的最大纵向力较小，即减速度较小，在相同的初始条件下，在低附着路面时需要更远的制动距离；2)目前的安全距离模型，未考虑前车运动状态，并假设前方障碍车和自车具有相近的速度，均未考虑驾驶员或者乘客心理因素.

针对目前汽车安全状态判断模型中存在的问题，文中提出一种改进的安全状态判断模型，综合考虑汽车行驶过程中的路面附着信息、前车运动状态信息、驾驶员乘客等心理安全因素和道路交通法规的影响，并建立安全距离模型.

1 路面附着系数识别

目前，路面附着系数的识别方法大致可以分为两类：基于原因的识别方法(Cause-based)和基于效果的识别方法(Effect-based)[7].Effect-based识别算法[8]是一种基于汽车动力学参数响应的间接路面附着系数识别算法，根据汽车制动过程的动力学响应，识别当前路面附着系数.

汽车在制动的过程中车轮的滑移率s和利用附着系数p的计算公式如下.

(1)

(2)

式中：ω为轮速；r为车轮滚动半径；V为车速；Fx为地面对车轮的纵向力；Fy为地面对车轮的侧向力；Fz为地面对车轮的法向力.

假如汽车在直线制动的情况下，忽略地面给车轮的侧向力，则有：

(3)

不同附着系数的路面s-p如图1所示，从图中可以看出，在滑移率较小时，轮胎的滑移率和利用附着系数满足一个线性的关系.文中在进行路面附着识别时，仅利用轮胎在线性区域时的汽车动力学模型对路面附着情况进行辨识.

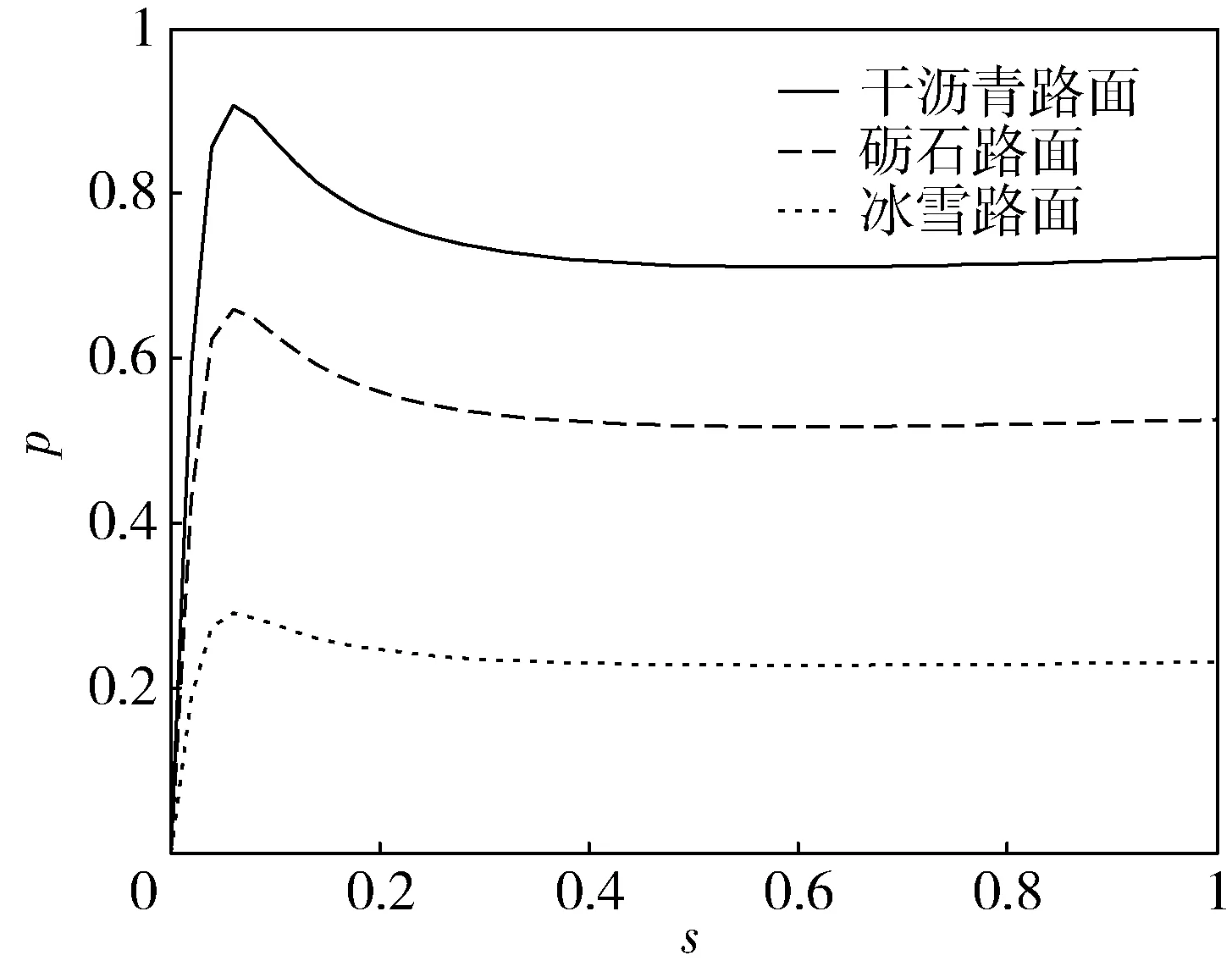
图1 路面附着系数s-p曲线

根据前面建立的魔术轮胎模型，汽车在道路行驶时，在轮胎滑移率较小时(滑移率满足0≤s≤0.05)，轮胎的滑移率和路面附着系数成正比，这时利用附着系数可以表示为

(4)

式中：K(μ)为滑移率与路面附着系数曲线的斜率.

从图1中可以看出，在高附着路面上，K(μ)值较大；在低附着路面上，K(μ)的值较小.假设轮胎处在线性区域，如果可以识别出这时的K(μ)，就可以计算出路面附着系数的值.

将汽车纵向动力学模型改写成如下式所示：

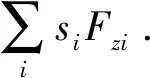
(5)

整理为最小递归二乘法的基本形式：

y(t)=φT(t)θ(t)+e(t)，

(6)

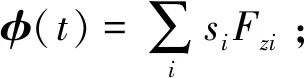
汽车的行驶状态是一个动态变化的过程.因此，为了跟踪时变的参数，提高估计精度，同时为了后面识别的结果可以反映前面的变化，采用递推最小二乘法进行识别[9].带遗忘因子的递推最小二乘法能够通过遗忘因子的选择加强新数据提供的信息量、减弱旧数据对系统模型无关性的影响，防止数据饱和等特点，步骤如下.

(1)初始化参数θ(0),P(0)，以及遗忘因子λ.一般取θ(0)=0或极小的数，这里取θ(0)=0，P(0)=106(值越大收敛速度越快)，遗忘因子λ取值范围为0.9≤λ≤1，这里取0.95；

(2)测量系统输出y(t)，计算回归矩阵φ(t)；

(3)计算估计误差：e(t)=y(t)-φT(t)θ(t-1)；

(4)计算增益矩阵K(t)：

(5)计算协方差矩阵：

(6)更新估计参数向量：θ(t)=θ(t-1)+K(t)e(t)；

(7)每个时间拍重复步骤(2)-(6).

采用这种方法估计出来的路面附着系数会存在一定的波动，因此,为了获得平稳的估计值，需要进行滤波处理[10].如图2所示，假设路面附着系数的初始识别为μ*，如果μi-μ*大于等于一个预先设定的门限值Δ1，则计数器k增加1，增加m个周期以后更新估计值；同理，如果μi-μ*小于等于预先设定的门限值Δ2，则L增加1，当增加到n个周期的时候更新估计值.否则，估计值μ*保持不变.通过这种改变更新周期m和n的大小，即可以调整估计值更新的频率，进而得到滤波的效果.其算法流程如图2所示.

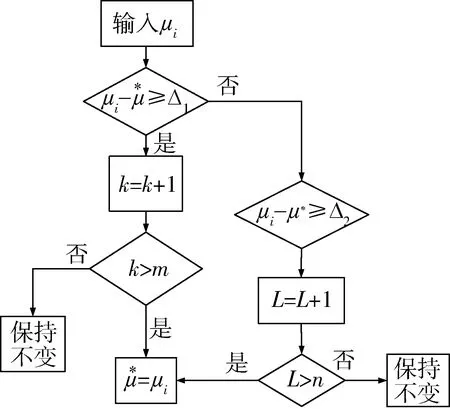
图2 路面识别滤波算法

为了验证所设计的路面识别算法和滤波算法的有效性，设置3种不同的路面情况来验证，验证结果如图3、4、5所示.

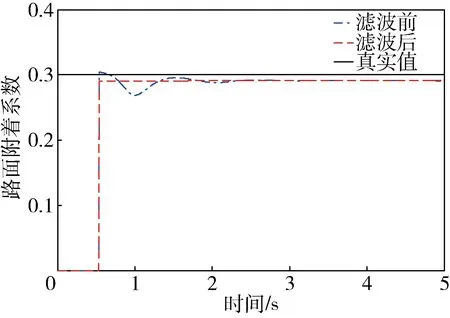
图3 路面附着系数μ=0.3识别效果

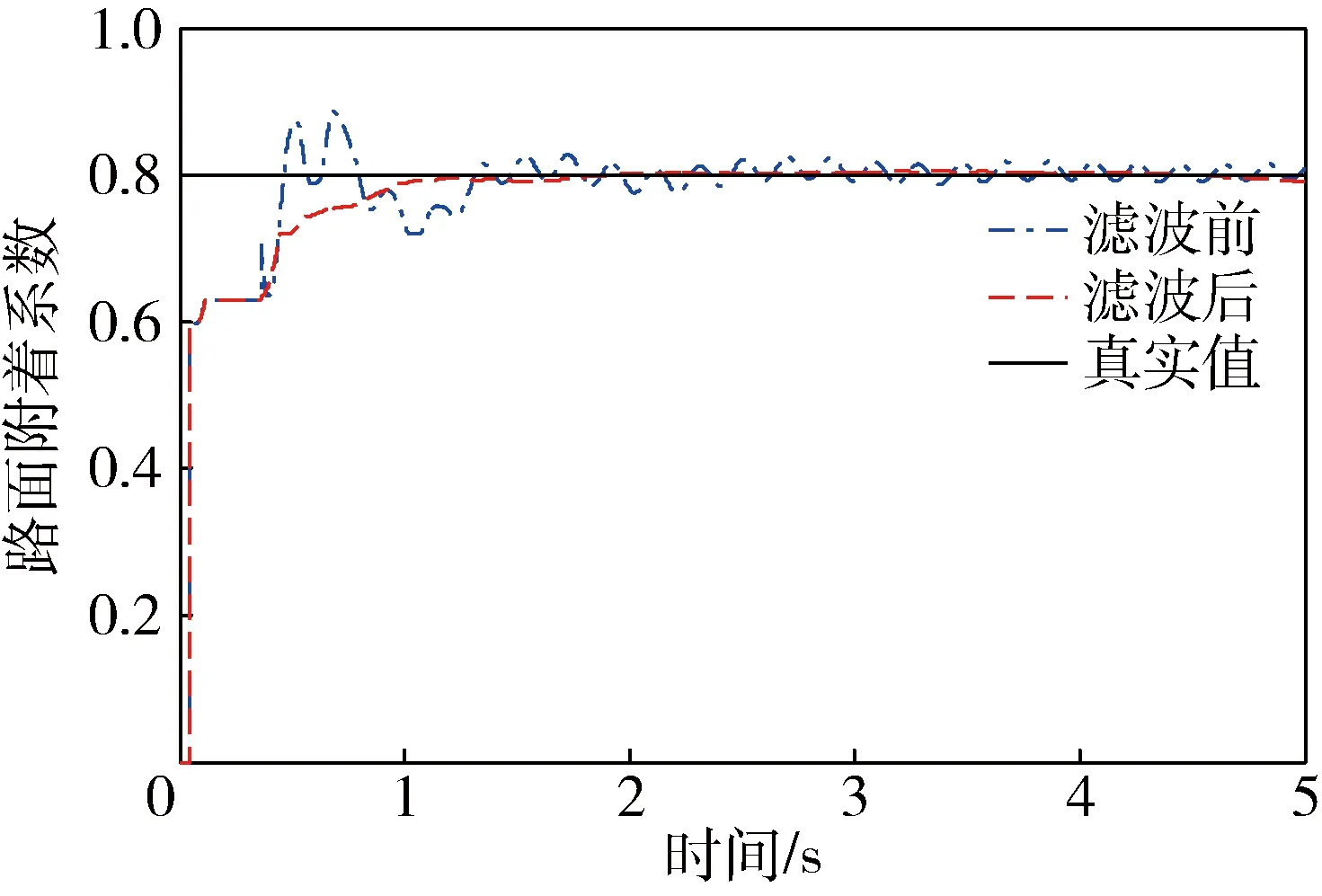
图4 路面附着系数μ=0.8识别效果

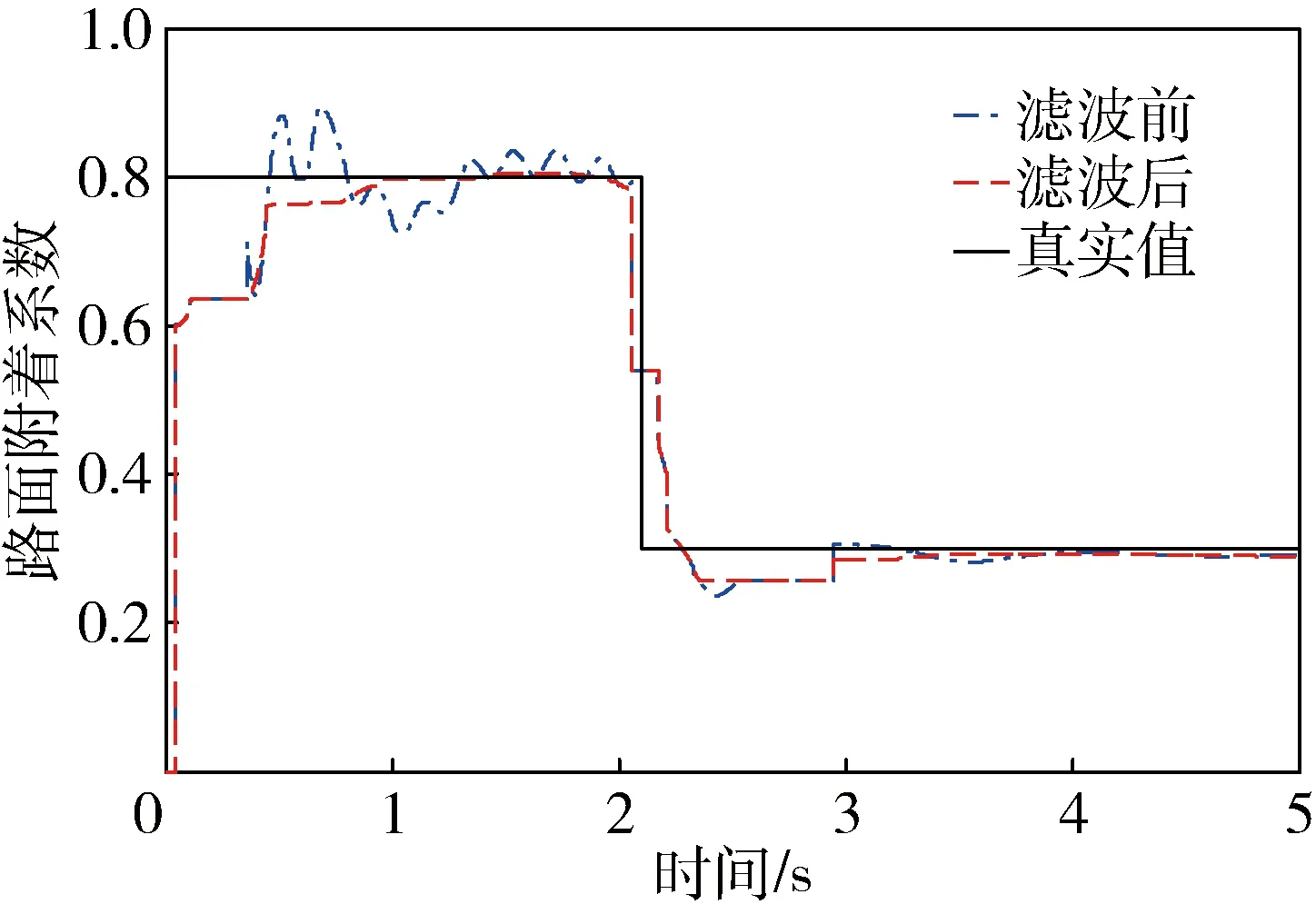
图5 变附着系数路面识别结果

图3和4是在固定附着系数的路面的识别结果，从图中可以看出，该算法在初始时刻有一定的波动，但最后的识别结果是在设定的路面附着系数附近.图5是变附着系数路面的识别结果，从图中可以看出，该算法在路面附着出现变化的时候有一定波动，但是总体的识别效果也较为理想.综上这3张图可以看出，所设计的路面附着系数识别算法和滤波算法具有良好的识别效果，识别稳定可靠.

2 安全距离模型建立

考虑如图6的避障场景，在这种情况下，不满足换道条件，自车只能通过制动避障来保持汽车安全行驶.

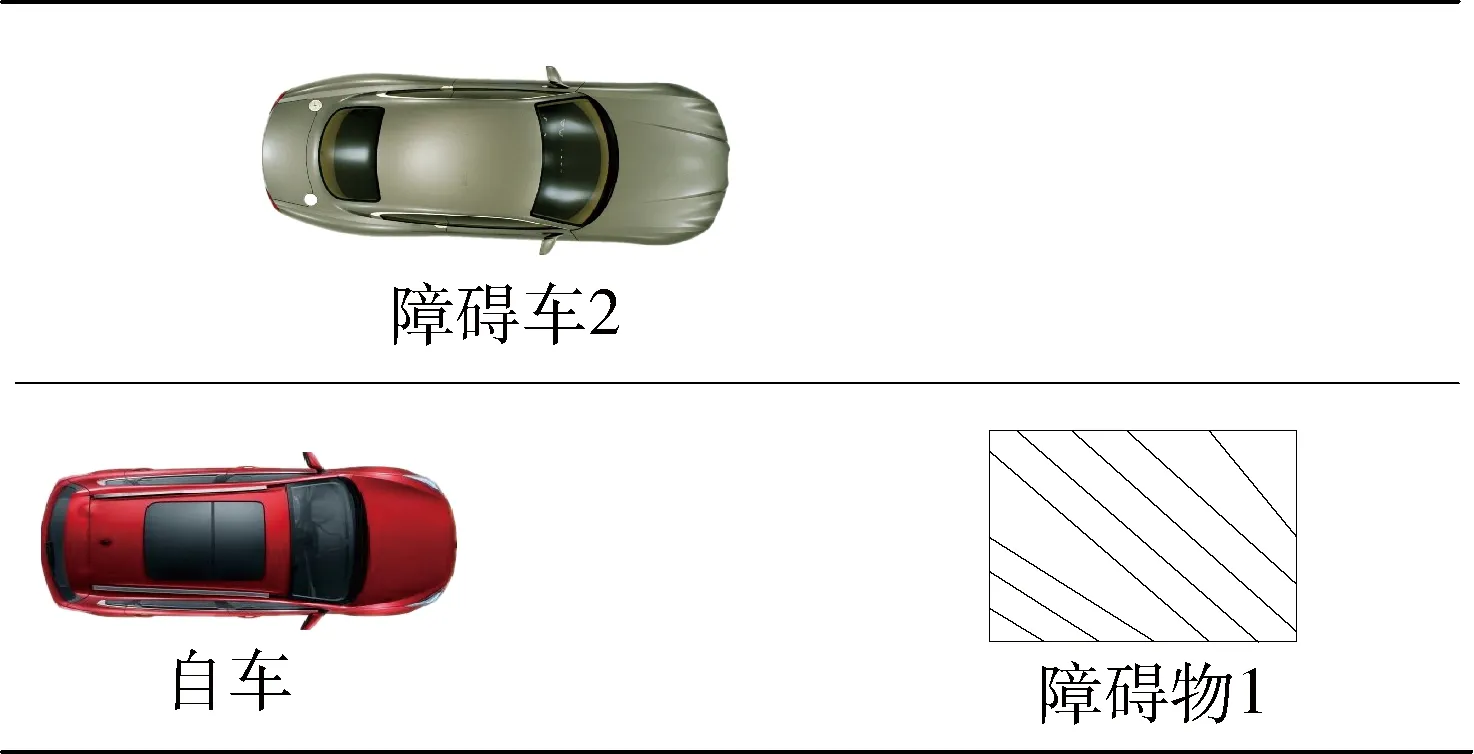
图6 汽车制动避障场景

一个准确的安全距离模型对于行车是否安全有很大的影响，文中在对汽车的纵向避障过程分析的基础上，提出汽车避障过程中纵向距离的3种状态：安全车距、预警车距和主动制动车距.根据状态的不同分别进行了分析和建模.图7表示车辆一般的制动避障过程.

根据汽车制动过程分析，安全距离可保证自车在任何工况都可以有充足的时间反应并做出相应的动作来保证车辆安全行驶的距离，因此，关于安全距离的计算需要考虑路面附着、前车状态、驾驶员反应和制动作用过程的延迟等因素的影响.因此，车辆安全距离模型如下式所示[1].

(7)

式中：tr、td分别表示主动制动系统的反应时间和制动协调时间，tr一般为0.5 s，td一般为0.2 s；v1表示自车的行驶速度；v2表示前车的行驶速度；μ表示路面附着系数；g表示重力加速度；s0表示停车时自车与前车安全车距，一般为车身长度；a1为自车最大减速度；a2是前车最大减速度，一般取a1=6 m/s2，a2=8 m/s2.

同理，可以得到报警车距为

(8)

同样可以得到汽车主动制动车距为

(9)

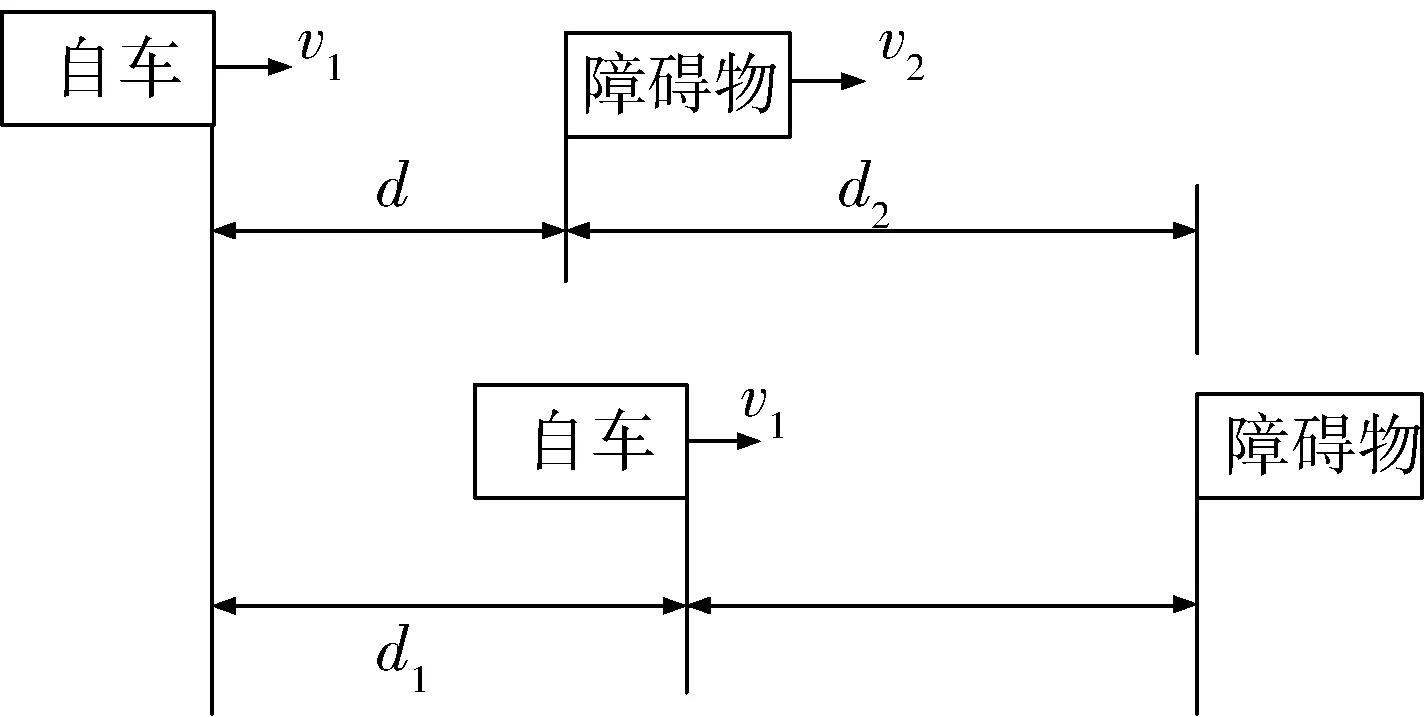
图7 制动避障过程

基于制动过程分析发现，该方法虽能在一定程度上反映汽车安全状态，但是并未充分考虑路面附着系数的影响、两车速度相差不大的情况以及道路交通法规的影响.因此，针对以上问题，建立改进的安全距离模型如下.

(10)

(11)

(12)

式中：η表示报警系数为0.8，ζ表示安全系数为0.6，车速单位为m/s.

改进的模型与原有的模型相比，根据两车车速对安全距离模型进行了区间的划分，同时引入了路面附着系数，并根据《中华人民共和国道路交通安全法实施条例》：在高速公路上行驶时，应当与同车道前车保持一定的时距，文中取k=3.6.改进的模型可以保证自车与前车始终保持一个合适的距离，虽然原模型可以保证两车保持一个安全距离，但某些工况会使两车相距较近，会使驾驶员感觉不安全，引起心理负担.

3 安全距离模型仿真

为了验证所建立的安全距离模型，搭建了Carsim和Simulink联合仿真模型.在Carsim软件中,建立整车动力学模型，自车为C-class级轿车，障碍车为B-class级轿车，Carsim输出参数包括前车速度、自车距前方障碍车的距离及自车速度等.在汽车距障碍物的实际距离小于预警距离时，采用PID控制施加期望的制动力保证汽车安全行驶.

工况一：前车以40 km/h匀速行驶，路面附着系数为0.8，自车与前方障碍物的初始距离为50 m，自车初速度为80 km/h.仿真结果如图8、9所示.

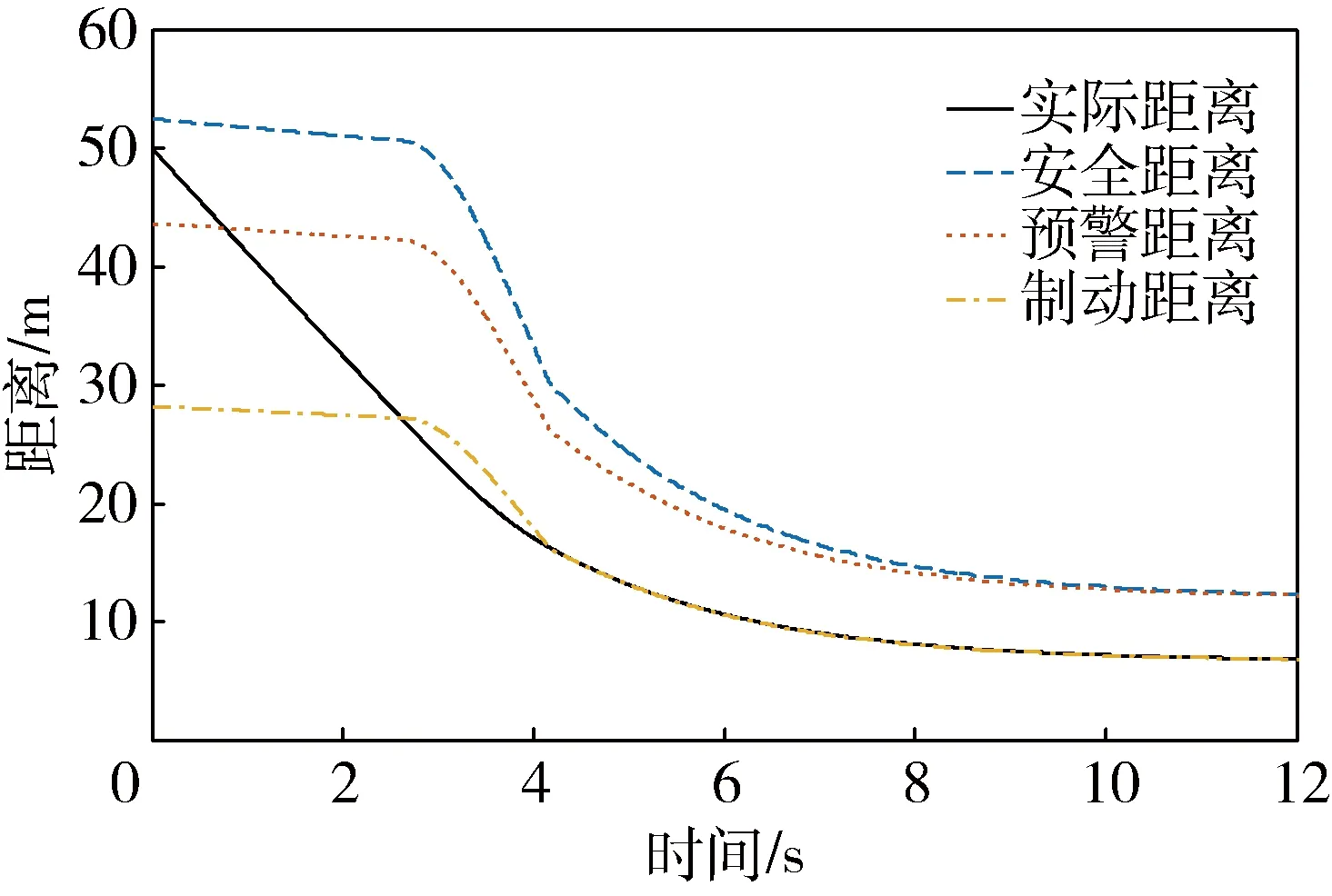
图8 安全距离(工况一)

从图8中可以看出，当汽车实际的距离小于建立的主动制动距离时，该系统能够及时地做出反应，来保证汽车安全行驶，汽车的实际距离也保持在主动制动距离附近，说明此时汽车能在保证安全行驶的同时保证道路交通利用率.图9是改进的主动制动距离模型和原模型在同一仿真工况下所计算出来的主动制动距离，从图中可以看出，汽车在3 s左右以后原模型计算出来的主动制动距离明显大于改进的主动制动距离模型计算的距离，虽然更远的跟车距离更能保证行车的安全性，但是却降低了道路交通利用率.

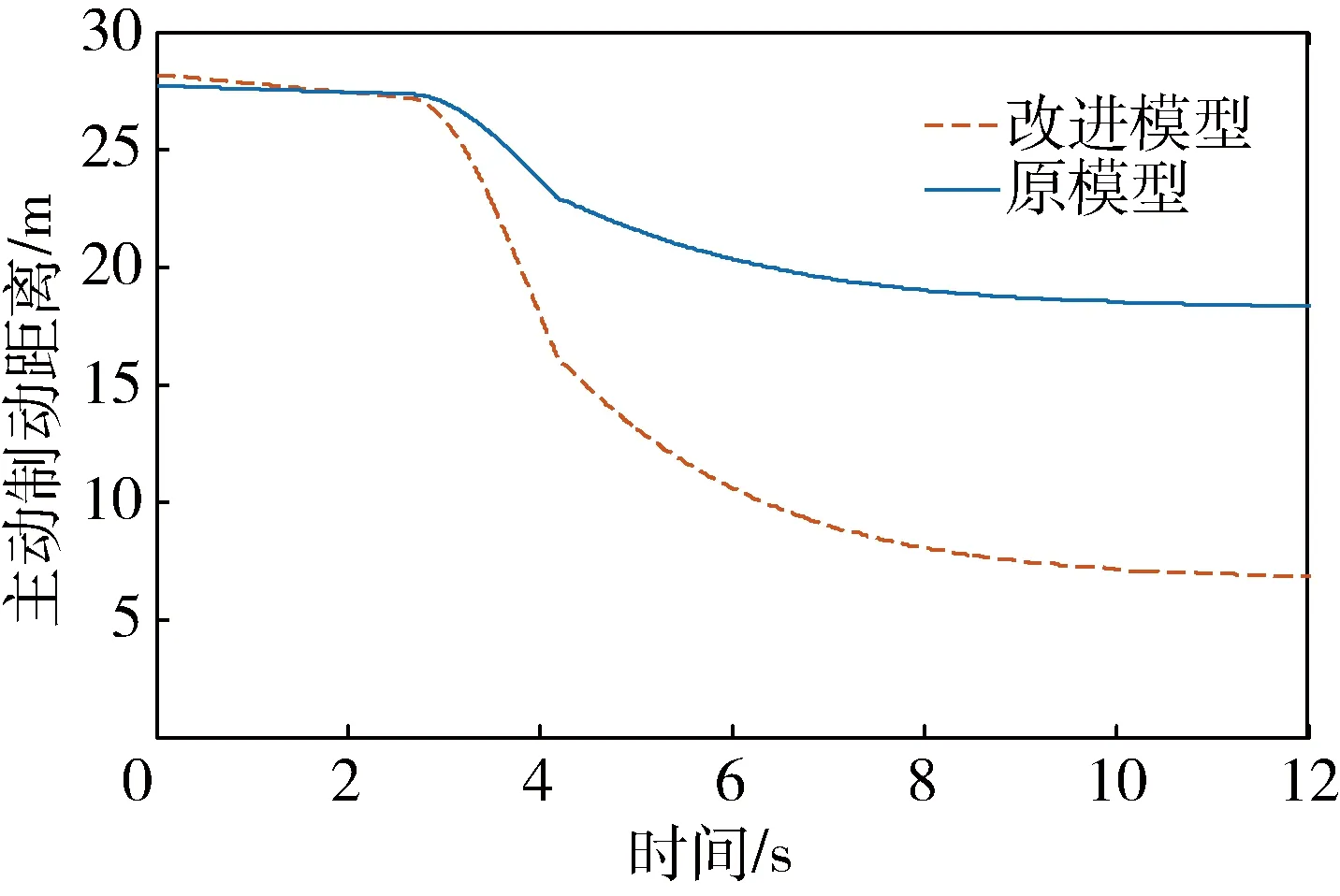
图9 主动制动距离对比(工况一)

工况二：前方车辆以40 km/h的恒定速度行驶，路面附着系数为0.4，自车初速度为80 km/h，两车初始间距为50 m.仿真结果如图10、11、12所示.

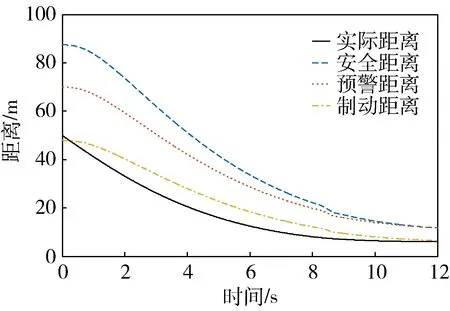
图10 安全距离(工况二)

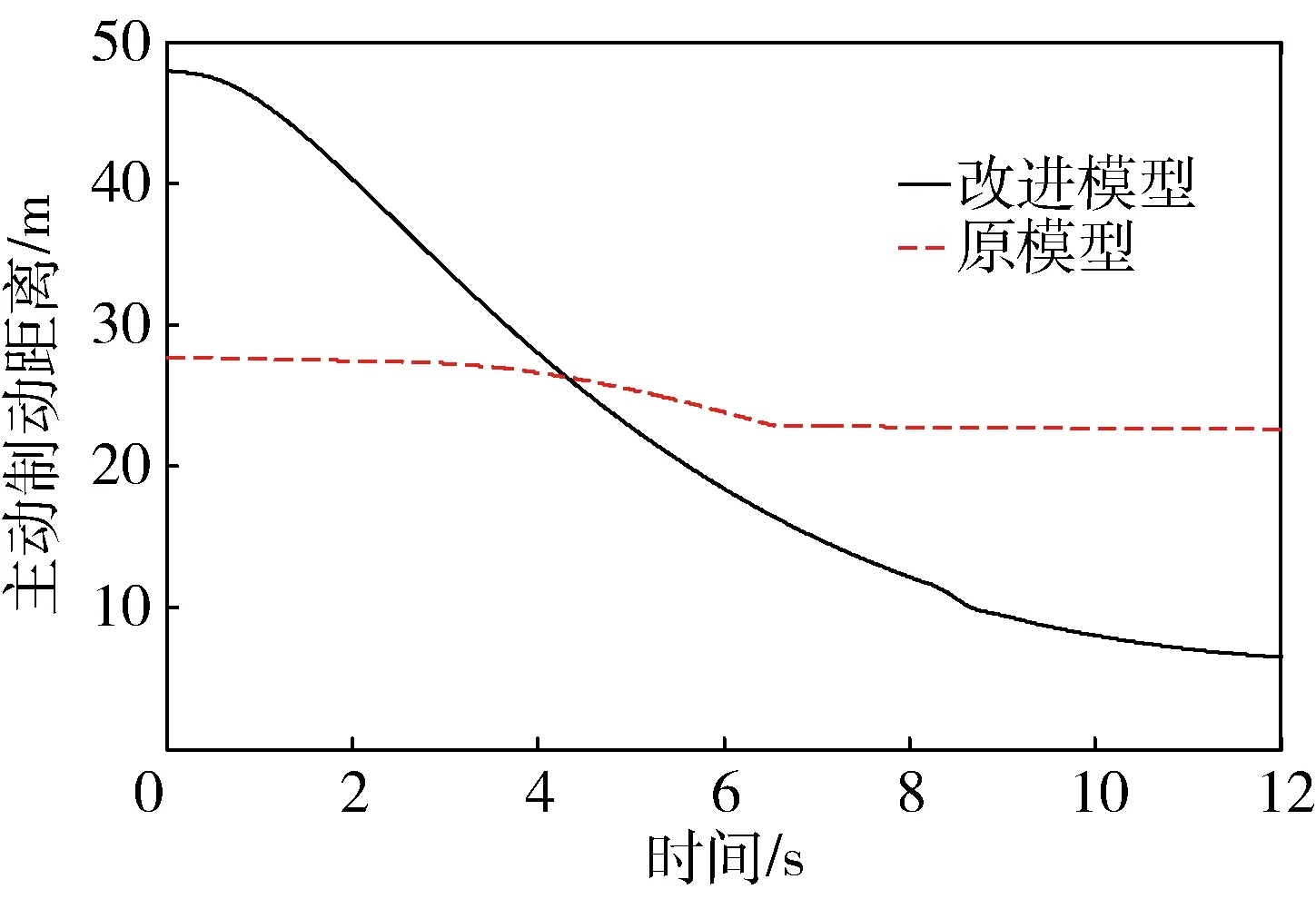
图11 主动制动距离对比(工况二)

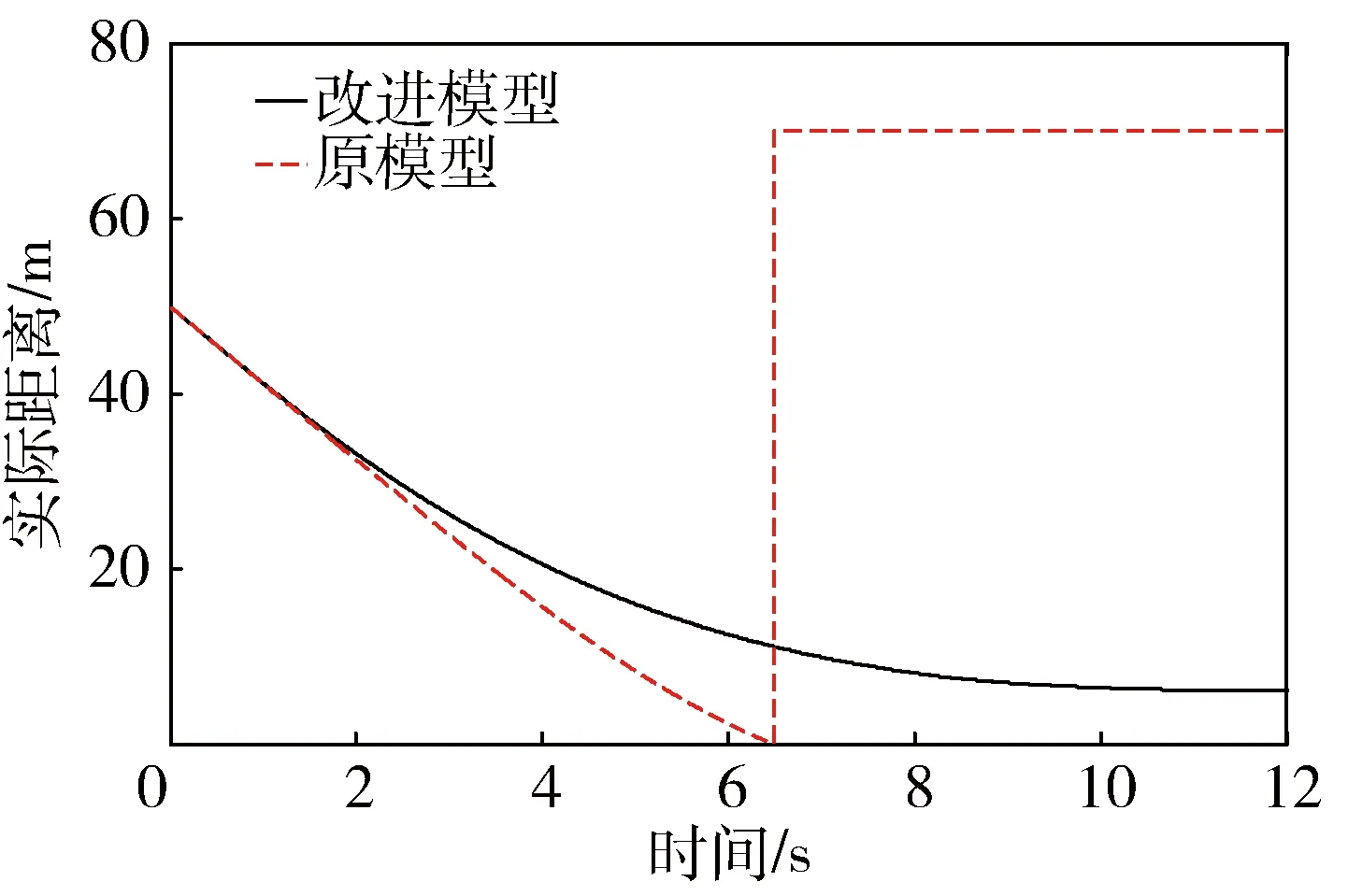
图12 实际距离对比

从图10中可以看出，系统能够及时的做出反应，使实际距离稳定在主动制动距离附近，保持跟车稳定性的同时提高道路利用率.图11为原模型和改进模型所计算的期望主动制动距离对比图，从图中可以看出原模型在路面附着系数低的情况下，计算的主动制动距离和高附路面一样，这样就会导致汽车错误的判断安全状态，造成追尾危险.从图12中我们可以看出，在6.4秒时原模型中自车和前方障碍物的距离已经到零，之后迅速增大，这是因为在6.4秒的时候，自车已经和前方障碍车发生碰撞并超过前方车辆，自车雷达最远测距为70 m.而改进的模型中，自车可以及时的判断危险状态，做出相应的动作，使自车和前方障碍物保持一个安全的距离.

4 实车试验

图13为制动实验平台，主要包含以下几个部分.

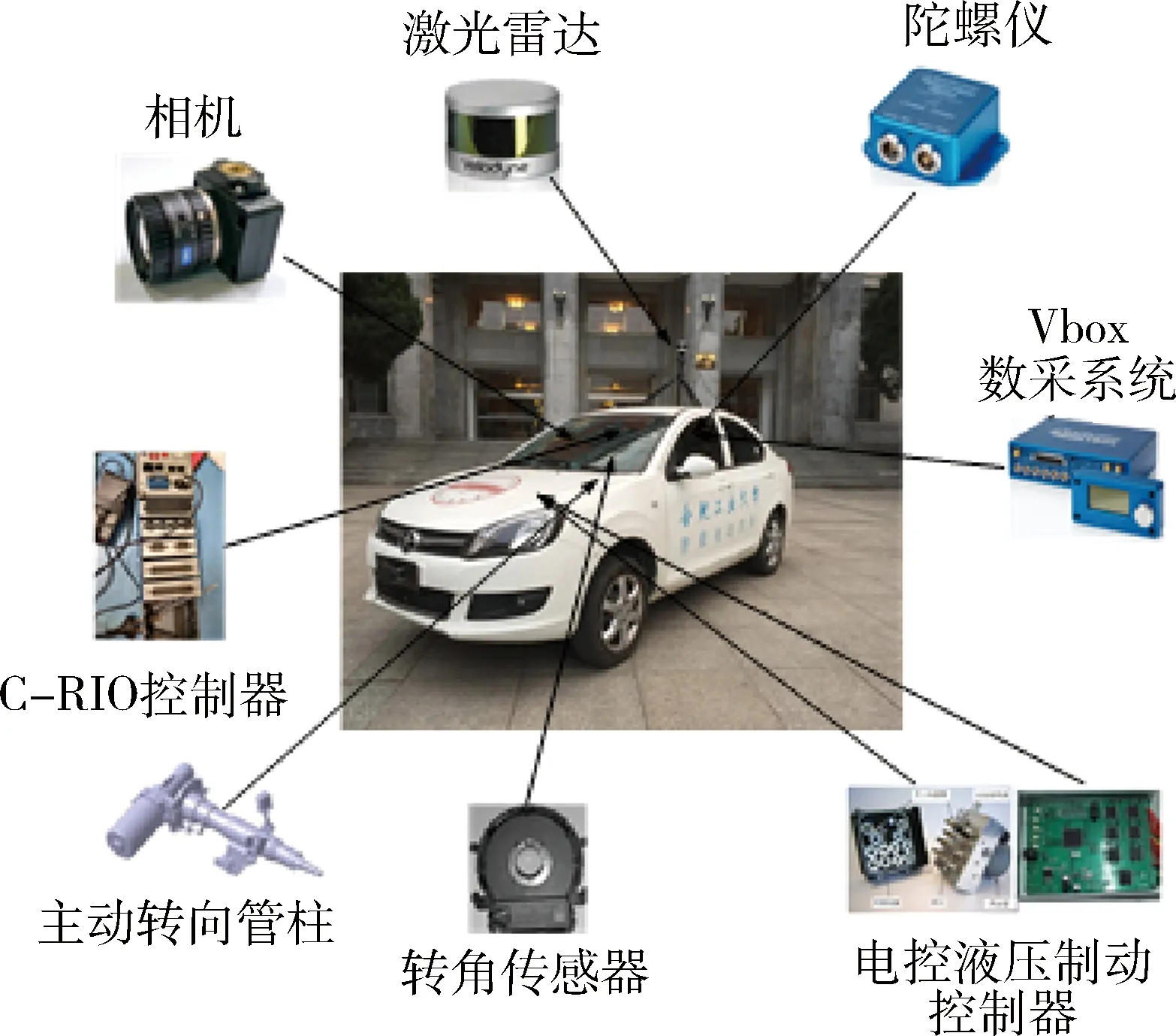
图13 实验车平台

汽车主动制动试验控制流程如图14所示：激光雷达将测得的障碍物信息通过CAN传递给车载c-RIO控制器，当控制器计算出存在可能碰撞的危险时，即将计算的期望制动压力信号传递给控制板，进而控制汽车进行主动制动避障.

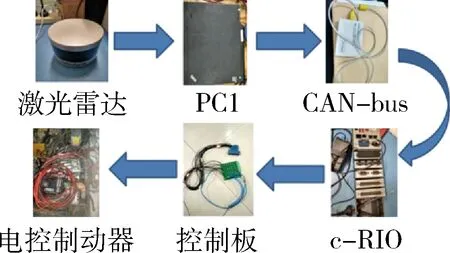
图14 实车实验控制流程

实车实验在良好的沥青路面上进行，前方存在一个固定的障碍物，自车初始速度为40 km/h，实验结果如图15、16所示.

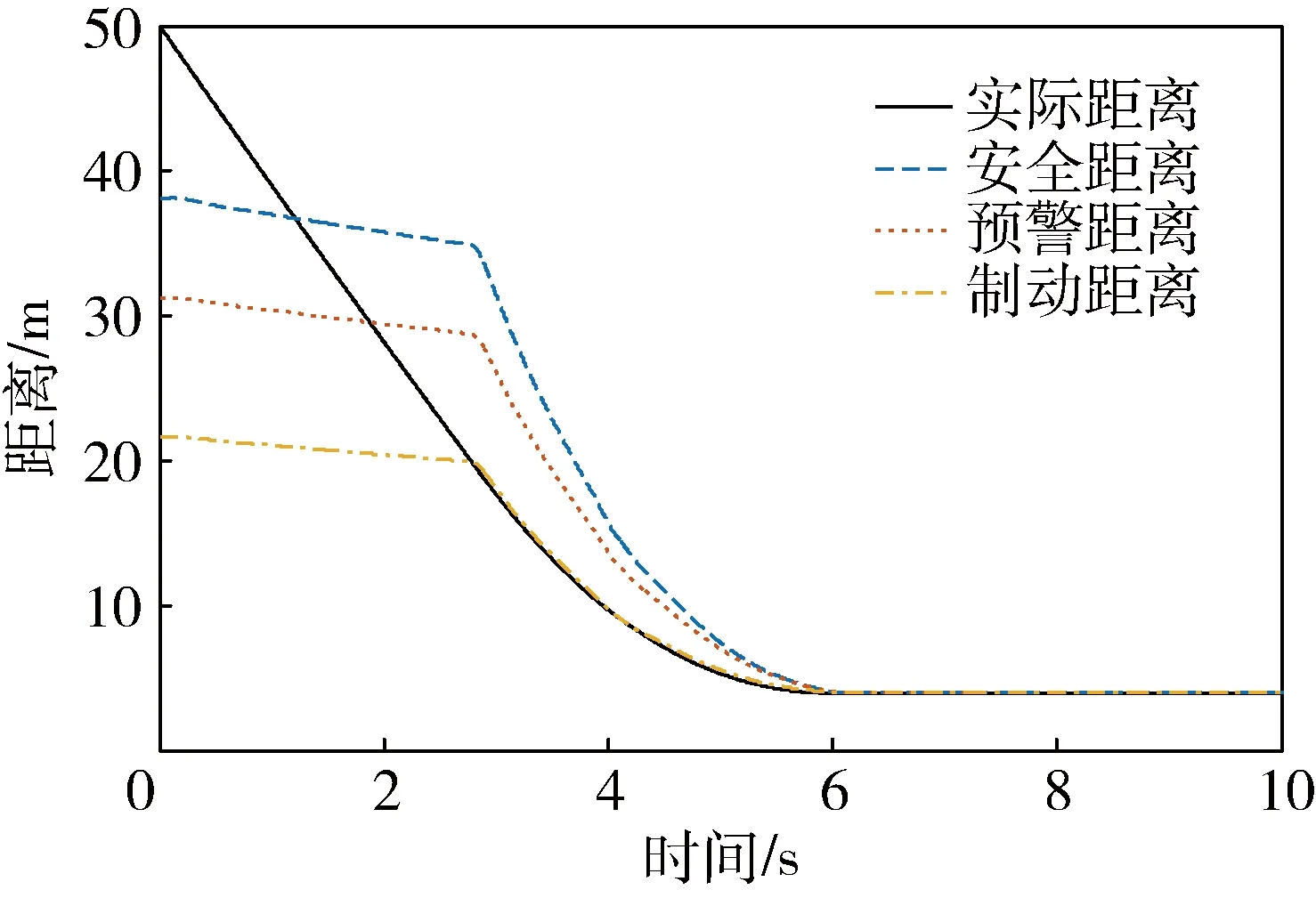
图15 实车实验距离对比

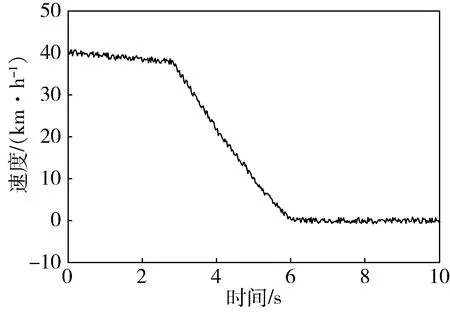
图16 实车速度

从图15中可知，在进行实验时，所建立的安全距离模型能够使汽车最后停车并和前方静止障碍物保持一个安全的车距.图16是这个过程中车速的变化，从中可以看出汽车制动过程平稳.

5 结 论

1)文中在考虑汽车主动安全方面，对已存在的安全距离模型缺陷分析的基础上，提出一种考虑路面附着影响和前方障碍物速度的安全距离模型.

2)在进行路面附着系数识别的时候，采用一种基于递推最小二乘法的路面附着系数识别算法，并通过仿真验证了其有效性.

3)在高附着和低附着路面工况下分别对提出的安全距离模型算法和传统的安全距离模型进行了仿真对比，仿真结果表明，所提出的安全距离模型能够在保证汽车安全行驶的同时，保证道路交通利用率.