定向延迟组合激发正演照明方法及应用
冯浩宇, 俞海龙, 王 典, 刘 财
(吉林大学 地球探测科学与技术学院,长春 130026)
0 引言
随着地震勘探程度的不断深入以及地震勘探方法技术的发展,人们对地震数据采集的质量、数据处理方法和数据解释的合理性具有越来越高的要求,其中野外地震数据的质量尤为重要,要想采集到准确的、高质量的野外地震数据,就应该针对不同的地质目标体,设置恰当的观测方式,采用合理的采集参数[1],才能更多的获取到所要研究的目标体的地质信息,对于那些地质构造复杂的地区,应用地震定向照明分析技术,可以有效的解决在地震数据采集中所存在的问题。
积分方程法、射线追踪法和波动方程法是目前地震数值模拟三种常用的方法,射线追踪法由于缺少地震波动力学信息以及高频近似和奇点问题,当地质构造变得复杂时会产生很大的计算误差,积分方程法由于受几何形态地影响较大,使其难以在实际中得到应用,而同时用到了地震波运动学和动力学信息的波动方程的地震数值模拟方法,能够很好地适应横向速度强烈变化介质,与实际中所观测到的地震波场非常接近[2]。因此,我们进行声波的波动方程数值模拟[3-4],进而实现基于声波波动方程的定向照明分析。
地震照明分析是通过地震波场数值模拟的方法来研究地震波在地下介质的传播规律和能量分布的定量分析方法[5],通常采用对地震波场的角度域分解或震源直接激发产生定向地震波场两种方法来实现定向照明分析,对于波场的角度域分解方法,Wu等[6]利用Radon 变换方法分解平面波并获取了波场的角度域信息,Xie等[7]利用小波变换分解波场的方法来获得角域信息,并将地震波在地下介质中的能量分布作为照明度,用于地震定向照明分析,裴正林[8]根据地震波能量理论,对地震波场进行方向性分解,并给出了地震波定向照明度的计算方法,计算出了基于声波方程的震源定向照明度和源-检定向照明度,Mao等[9]提出了一种基于局部指数标架的局部角度域地震定向照明分析方法,通过局部余弦和正弦变换的线性组合将不同发射接收系统的空间域波场分解为局部角度域,该方法相比于传统的方法具有更高的效率,耿瑜等[10]在局部指数标架角度域方向照明的基础上,将方向照明分析应用在盐丘下部目标区域上,研究采集系统对成像质量的影响,从而达到提高成像质量的目的,冯伟[11-12]、陈生昌[13]、谢小碧[15]、Tao等[14]也采用不同的变换方法对地震波场进行角度域分解,实现了对地下介质的定向照明分析。对于直接产生定向地震波场方法,王忠仁等[16]利用有限差分法对相控震源chirp信号扫描的地震响应进行了数值模拟,得到了相比于常规组合激发方法更好的信号,为了提高原始地震数据的信噪比,姜弢等[17-18]提出了一种基于可控震源阵列的定向照明控制方法,Tomas等[19]对组合震源激发原理进行了系统的总结,并给出了其在提高地震分辨率的应用,蔡纪琰等[20]利用4种常用的震源进行了波动方程有限差分正演模拟,从理论上研究了不同激发方式在震源药量相同的情况下的波场传播特征,以及所对应的能量照明关系,巩向博等[21]给出了在地表起伏条件下,组合震源所产生的定向地震波场的计算方法,秦龙[22]提出通过增加炮点的数目来提高地震照明的均匀性[22]。
对于角度域分解法,由于需要对地震波场逐点进行角度域分解以便获得角度信息,因此计算量大、计算效率低,对于直接产生定向地震波场方法,大多采用一阶压力-速度声波方程,相比于二阶声波方程,涉及公式多、编程实现难度大、计算效率低,鉴于此笔者直接基于二阶声波波动方程,利用规则网格有限差分技术对声波波场进行正演模拟,通过改变组合震源的数目来控制地震波主波束的集中程度、通过改变组合震源之间的激发时间,来调整地震波主波束的方向,然后计算地震波场能量在地下的分布情况,进而实现定向照明分析。
1 方法原理
基于二维声波方程采用时间2阶空间10阶的规则网格有限差分进行正演模拟,在二维空间域内,声波方程为式(1)。
(1)
式中:u为声波波场;v为声波速度;t为时间;x、z为空间坐标。
由于实际正演模拟的区域是有限的,当地震波传播到边界时会发生强烈的边界反射,严重影响着计算结果的准确度,完全匹配层(Perfectly Matched Layer,简称PML)吸收边界条件能能够很好的消除边界反射的影响,其基本思想是在所研究区域的边界上加上吸收衰减层,使地震波传播到边界时不会发生反射,并且在吸收区域地震波会快速衰减,以此来减弱边界反射所带来的影响。
我们采用的是王维红等[3]提出的完全匹配层吸收边界条件,其给出的二维声波方程完全匹配层的控制方程为式(2)。
(2)
式中,A(x,y)为吸收衰减因子,在实际正演模拟区域中,衰减因子A(x,y)为零,式(2)和式(1)完全相同,此时波场传播满足声波方程,在PML区域中,衰减因子A(x,y)不为零,地震波无反射的进入该区域后会快速衰减。
图1为完全匹配层示意图,内部区域是实际地震波场正演模拟的区域,在该区域中x和z方向的衰减因子均为零,在PML区域1、2、3中衰减因子均大于零,陈可洋等[23]提出的余弦衰减因子,其表达式为式(3)。
lx=0,1,2,…PML
lz=0,1,2,…PML
(3)
式中:B为衰减幅度因子;αz表示沿z方向即PML区域1中的衰减因子;αx表示沿x方向即PML区域2中的衰减因子;PML区域3中的衰减因子为αx+αz;PML表示吸收层厚度;lx和lz分别沿x和z方向网格点到边界的距离,从式(3)中可以看出,衰减因子随着点到边界距离的增加而逐渐增大,对应图1中的颜色逐渐加深。
由此可得到基于PML边界条件的时间2阶空间高阶(2K阶)有限差分方程:
(4)

图1 完全匹配层示意图Fig.1 Schematic diagram of complete matching layer

图2 未加边界条件的波场快照Fig.2 Snapshot of wave field without boundary conditions

图3 加边界条件的波场快照Fig.3 Snapshot of wave field with boundary conditions

图4 组合震源的方向性Fig.4 Directivity of the combined source
图2、图3分别是无边界条件和加入PML吸收边界条件的波场快照,从图2、图3中可以看出,当无边界条件时,波场传到边界会发生强烈的边界反射,对计算结果产生很大的影响,当加入PML吸收边界条件时,波场传到边界时无边界反射,具有很好地吸收效果。
如图4所示,地表有n个震源,分别为O1、O2、…、On,相邻两个震源之间的间距为d且保持恒定的相位差β,S是距离震源较远的位置处的一点,因此各震源到S点的射线可以看成是平行的,θ是射线方向与地表的夹角,由此可以得到S点来自相邻两个震源的地震波的相位差为ψ=kdcosθ+β,假设震源O1在S点产生的场强为E1,则震源O1、O2、…、On在S点产生的总场强为E=E1+E2+E3+…+En=E1(1+ejψ+ej2ψ+…+ej(n-1)ψ)=E1(sin(nψ/2)/sin(ψ/2))ejξ,式中ξ=((n-1)/2)ψ是总场强的相位角,与总场强的方向无关,因此可以取fa(θ)=sin(nψ/2)/sin(ψ/2),我们将fa(θ)称为组合震源地震波场的方向因子,当ψ=0时,fa(θ)取最大值,即
(5)
于是可以得到归一化的组合震源地震波场的方向因子F为:
(6)
其中:n为震源的数目;k为波数;d为相邻震源的间距;θ为传播角度;β为相邻震源间的恒定相位差。
当相邻两震源间的相位差(kdcosθ+β)发生变化时,地震波主波束方向会随之变化,主波束方向对应最大能量指向,所以最大能量的指向可以通过改变恒定相位差β来控制
θmax=arccos(-β/dk)=arccos(-βv/πfd)
(7)

图5 组合震源不同时间延迟的地震波场理论方向图Fig.5 Seismic wave field theory with different time delays in combination of earthquake source(a)n=5,τ=0.001 5 s;(b)n=5,τ=0.003 5 s ;(c)n=5,τ=-0.002 5 s(d)n=10,τ=0.001 5 s;(e)n=10,τ=0.003 5 s;(f)n=10,τ=-0.002 5 s
当相邻两震源间依次延时τ,则任意时刻引起的相位差为β=-2πfτ,由此引起的地震波主波束方向为:
(8)
由式(8可以得到选定地震波方向后,对应的延时时间为:
(9)
图5是震源个数分别为5和10,震源间距为10 m,地下介质速度为2 000 m/s,震源从左到右的延迟时间分别为0.001 5 s、0.003 5 s、-0.002 5 s所对应的地震波方向图。从图5中可以看出,不同的延迟时间,对应着不同的地震波主波束指向,且随着震源数目的增多,主波束指向更加集中。
假设位于(xn,zn)处的单个震源激发产生的地震波场在地下任意一点(x,z)处的分布为Us(xn,zn;x,z,t),那么多个震源组合激发产生的地震波场Us(θ;x,z,t)为式(10)。

图6 水平层状介质模型Fig.6 Horizontal layered medium model

(10)
根据地震照明理论,组合震源在二维模型空间点(x,z)处的照明度为[17]式(11)。
(11)
2 数值算例
2.1 水平层状介质模型
图6是四层水平层状介质模型,速度从上到分别为1 000 m/s、1 500 m/s、2 000 m/s、2 500 m/s,模型大小为2 000 m×2 000 m,图7(a)、图7(b)、图7(c)是炮点个数为9,分别位于960 m到1 040 m,炮点间隔为10 m,激发延时为0 ms、3 ms、5 ms的照明结果。图7(d)、图7(e)、图7(f)为对应的波场快照,从图中可以看出,当炮点无延时激发时,波场垂直地表向下传播,能量延垂直地表向下分布,且随着与炮点距离的增加,能量分布范围逐渐变大;当炮点激发有延迟时,随着延迟时间的增加,能量传播方向与垂向角度逐渐增大,且地层速度越高,对应的角度越大。

图7 不同激发延时能量照明及波场快照Fig.7 Energy illumination and wave field snapshots with different excitation time delay(a)无时间延迟;(b)从左到右延迟3 ms;(c)从左到右延迟5 ms(d)无时间延迟波场;(e)从左到右延迟3 ms波场;(f)从左到右延迟5 ms波场

图8 逆冲推覆构造模型及照明结果Fig.8 Thrust nappe structure model and lighting results(a)逆冲推覆构造模型;(b)从左到右延迟7 ms;(c)从右到左延迟7 ms;(d)从右到左延迟8.7 ms

图9 Marmousi速度模型Fig.9 The marmousi model
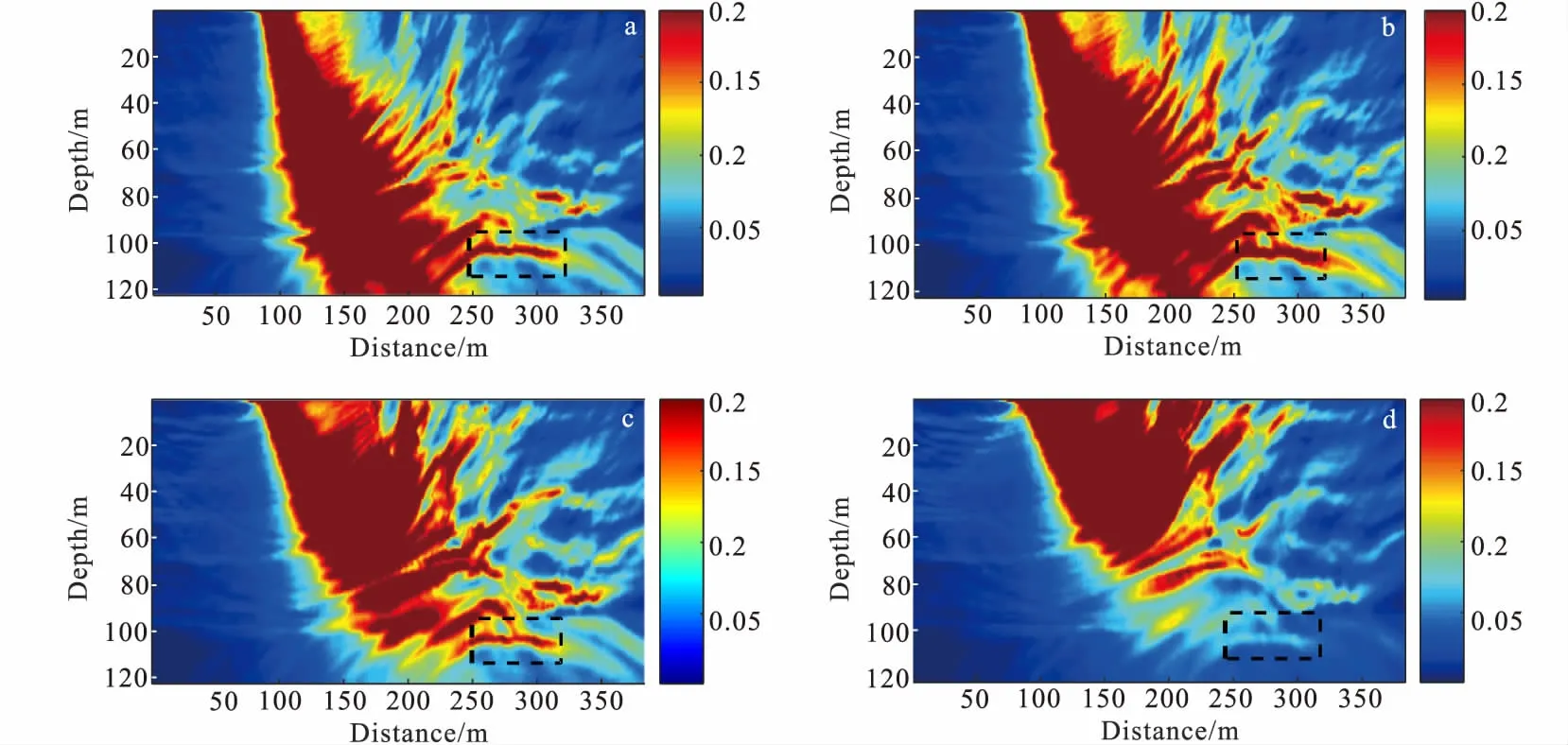
图10 不同激发延时照明结果Fig.10 Illumination results of different excitation delays(a)从左到右延迟5 ms; (b)从左到右延迟6 ms ;(c)从左到右延迟7.5 ms; (d)从左到右延迟9 ms
2.2 逆冲推覆构造模型
图8 (a)是逆冲推覆构造模型,从上到下各层的速度分别为1 000 m/s、1 500 m/s、1 800 m/s、2 200 m/s、2 500 m/s,模型大小为2 070 m×1 270 m,本文所要研究的是断层所在的区域,图(b)是炮点个数为9,分别位于460 m到540 m,炮点间隔为10 m,从左到右相邻炮点激发延时为7 ms的能量分布图,波场延与地表垂向向右夹角大约为45。方向传播,能量主要集中在此方向上,使其与断层方向大致平行,图8(c)是炮点个数为9,分别位于960 m到1 040 m,炮点间隔为10 m,从右到左相邻炮点激发延时为7 ms的能量分布图,波场延与地表垂向向左夹角大约为45。方向传播,能量主要集中在此方向上,使能量尽可能多的分布在断层所在的区域;图8(d)是炮点个数为9,分别位于1 460 m到1 540 m,炮点间隔为10 m,从右到左相邻炮点激发延时为8.7 ms的能量分布图,波场延与地表垂向向左夹角大约为60.5。方向传播,能量主要集中在此方向上,使能量尽可能多的分布在断层所在的区域,从中可以看出,采用上述方法设计炮点位置,能量主要分布在断层区域,可以获得更多的该区域的反射信息,进而能够很好的对该区域进行深入的研究。

图11 目标层不同激发延时能量曲线Fig.11 Different excitation delay energy curves of the target layer
2.3 marmousi模型
图9是二维复杂的marmousi速度模型,模型大小为1 220 m×3 840 m,模型上部有三条大的断裂,中部有一盐丘,深部靠近模型的左右两侧有两个高速异常体,在深度1000 m ~1 100 m、水平2 500 m ~3 000 m位置处存在一低速目标层,网格点数为122×384,网格间距为10 m,时间步长为0.5 ms,采样时间为2.0 s。图10是采用雷克子波(主频为30 Hz),炮点个数为9,分别位于1 380 m到1 540 m,炮点间隔为20 m,从左到右相邻炮点激发延时间分别为5 ms、6 ms、7.5 ms、9 ms的能量分布图,所要研究的目标区域为图中黑色虚线所在的低速区域,从图9中可以看出,在相同震源数目的情况下,组合震源不同的延迟时间,目标区域的能量分布是不同的,当延迟时间为6 ms时,目标区域的能量分布明显高于延迟时间为5 ms、7.5 ms和9 ms所对应的能量分布,因此,在实际野外勘探时,为了得到目标区域而更多的反射信息,获取高信噪比的数据,延迟时间应设置为6 ms。
图11是在深度为1 040 m、水平方向为2 500 m~3 000 m处的组合震源不同激发延时的能量曲线,从图11中可以看出,延迟时间为6 ms时目标层具有最高的能量分布,其余能量分布由大到小的延迟时间依次为5 ms、7.5 ms和9 ms,这也进一步说明延迟时间为6 ms时,可以获取更多的与目标层相关的反射信息,能够得到最佳的勘探效果。
3 结论
1)基于二阶标量声波波动方程,利用规则网格有限差分技术,对声波波场进行正演模拟,相比于一阶压力-速度方程容易编程实现、计算效率高。
2)采用组合震源的激发方式,通过改变相邻两个震源之间的激发延迟时间来产生定向地震波场,进而实现组合震源定向照明分析,从层状介质模型试验中可以看出,延迟时间越大,能量传播方向与垂向夹角越大,地层速度越高对应的角度也越大。
3)将定向照明方法应用于复杂的逆冲推覆构造模型和marmousi速度模型中,对于不同的炮点位置,通过改变激发时间来实现对目标区域的照明分析,当炮点位置相同时,可以通过调整激发时间来获取最佳的照明效果。
4)笔者是在二维水平地表的情况进行研究的,当地表起伏时该方法不再适用,此后会将该方法推广到起伏地表和三维模型中,以便更好地满足实际勘探的要求。

