广义S变换时频分析在广域电磁法数据处理中的应用

吴 桐， 李帝铨， 索光运， 房 瑞

(中南大学 地球科学与信息物理学院，长沙 410083)

0 引言

电磁法作为地质勘探当中重要的手段，在实际应用中不可避免地会受到各式各样的干扰而无法获得理想的有效信息，特别是在干扰强的地区无法区分噪声和有效信号[1-3]。因此，在噪声条件下提取有效信号显得尤为重要。电磁信号处理的过程中，主要基于傅里叶变换获得信号的频谱进行信号的分析。由于傅里叶变换是所有频率成分在总时间上的集成，获得的频谱响应很容易受到噪声的影响，仅采用傅里叶变换难以获取真实有效的信息。为了提高有效信号的挖掘能力，在时间尺度进行时间-频率的分析就很有必要[4-7]。

时频分析主要描述信号的频谱随时间的变化，理想情况下，时频分析可提供每个时间点下精确的频谱信息，基于此国内、外学者进行了大量的研究，提出了多种时频分析方法。S变换是由Stockwell[8]提出来的时频分析方法，结合了短时傅里叶变换和小波变换，它既含有快速傅里叶变换的相位信息，同时又保留了小波变换的多尺度分辨能力，是两者的延伸和推广。在实际应用当中，S变换对时频分析的分辨率调节力度不够，能量聚集性不足，许多的学者又对S变换进行了研究，提出了不同的广义S变换。周竹生等[10]将可调因子引入S变换，Djurovic＇ 等[11]提出了最优化S变换；Pinnegar等[12]提出了可调节时-频分辨率的改进S变换；陈学华等[9]改进了S变换；Robert Pinnegar[12]提出了两种频率函数来控制变换窗口的广义S变换。笔者采用离散信号可分辨最高频率Fmax为线性因子，基于可变因子广义S变换的思想，提出基于广义S变换的广域电磁信号处理流程，并把此方法应用到广域电磁信号处理中。

1 广义S变换

1.1 S变换

S变换是Stockwell提出来的方法，是一种时频谱局部化的方法，类似于短时傅里叶变换，信号h(t)的S变换定义为式(1)。

(1)

其中：τ为时间(s)；f为频率(Hz)；i为虚数单位。

S变换能写成h(t)的傅里叶变换H(f)的形式：

f≠0

(2)

其一维的连续逆变换为：

(3)

式(1)中S变换的高斯窗宽度与频率成反比关系,其时频分辨率是根据时频的变换而相应变化，高频时，信号变化剧烈，时域窗函数相应的缩小；低频时，信号变化缓慢，时域窗函数相应的扩展，以提高频率分辨率。因此，S变换有着类似小波变尺度的能力。式(2)表明S变换可以借助傅里叶变换形式提高自身计算效率。式(3)表明S变换有相应的逆变换，能进行时频相互转换，有较高的实用性。

1.2 广义S变换(GST)

理想的时频-分析表达(Ideal time-frequency representation，ITFR)指频谱特性随时间变化，其提供瞬时时间点上信号所有频率的信息，不与相邻时刻或者相邻频率信息的交叉，即其无论在在时间域还是频率域都有高分辨能力[13-15]。

时频-分析尽可能地接近于理想时间-频率的表达，获得高分辨率的时变频谱。由于S变换的窗函数是高斯窗，其随频率变化的灵活性不足，能量的聚集性不高，对时频分析的分辨率调节力度不够(如图1(e)、图1(f)所示)且很难达到理想的时频-分析表达的形式，所以众多学者提出了各式的广义S变换来提高其分辨能力。周竹生等对S变换做了改进增加可调因子令：

(4)

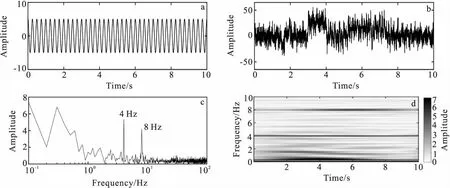
图2 含噪广义S变换时频-分析Fig.2 Waveforms of signal and results of general S-transform with noise(a)理论信号；(b)理论信号中加入三角波、方波噪声和-20 dB的高斯白噪声；(c)含噪信号傅里叶变换振幅谱；(d)含噪信号广义s变换时-频分析谱

参数σf能比较灵活的控制高斯窗口，σf有多种函数形式，如σf(f)=k/f+b、σf(f)=(k/f+b)2，k、b为常数。姬战怀[16]等联系了离散信号处理的过程，根据奈奎斯定理加入了离散信号最高频率Fmax，把Fmax加入到σf形式中去，形成：

σf(f)=α+βf/Fmax

(5)

式中，α和β为正实常数。其对比了多种广义S变换的效果，这种形式的常规广义S变换聚集效果较好，在时频-分析调节上有更大的灵活性，恰当地调节参数可以获得比较好的时频-分析的效果[17-21]。经过多次调节分析，信号提取方法常数参数都取α=0.4、β=4，表达式为式(6)。

(6)

2 仿真实验

人工源电磁法信号在无干扰的条件下，所获得的信号具有长周期、幅值稳定的特点[21]。但是实际测量的信号会受到各式各样的干扰，使得我们不能准确地获得有效信息。因此分析噪声的时频特性并采用合适的处理方法有助于提高数据质量。笔者采用广义S变换对广域电磁方法在干扰条件下的数据进行仿真实验，干扰源为电磁信号当中常见的方波、三角波、高斯白噪声[1-2]。

法律应当合理区分双方行为的市场范围，充分发挥他们在不同市场领域中的信息处理优势。实际上，宏观市场的调控、服务一直是我国政府的职责，只是在民间融资市场监管方面不明确。法律可明确把宏观市场作为监管者的行动领域，其主要职责是利用组织化、专业化能力优势，为民间融资主体提供宏观上的信息服务和引导，教育融资者在了解市场风险基础上自主决策，自担风险，理性行动；健全信用信息记录，建立信息共享平台，降低融资主体信息获取成本等。同时，法律应赋予监管者可以强制要求融资主体披露信息的权力、实行登记备案管理掌握市场动态的权力以及其他信息收集的权力。微观上主要是融资主体的活动空间，其在法律范围内自由行动。

定义4 Hz和8 Hz的余弦信号作为理论信号：

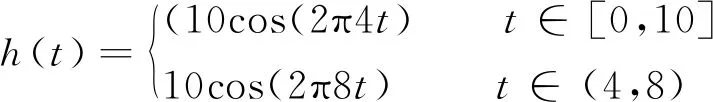
(7)

该信号的采样率为256 Hz，采样点数N为2 560。方波和充放电是电磁法时间序列数据比较常见的噪声，从图2(c)分析噪声主要集中于低频部分，从图2 (d)能分析出4 Hz长周期的信号一直存在，短周期信号8 Hz余弦信号在4 s到8 s存在，能确定噪声主要在2 s、4 s、6 s呈现一个干扰区域，而高斯白噪声则存在于所有的频点上。因此，通过分析时频谱避免干扰噪声区域来提取有效信号，对实际广域电磁方法比傅里叶变换更有优势。

3 广义S变换数据分析处理流程

广域电磁勘探中，发送信号为2n序列伪随机的信号[21-23]，其能量分布在以2为底的指数的主频信号上，且频率在对数坐标上均匀分布，这种良好的能量分布特性对于频率域电磁勘探非常适合，且能通过高强度、多周期采集压制的方式获得高信噪比的信号。针对广域电磁数据的特点，笔者设计了广义S变换在广域电磁数据处理的流程：

1)输入时间域数据，进行基本的傅里叶变换进行频谱分析。

2)根据傅里叶变换谱，选择对应不同频段要求的合适的广义S变换因子。

3)对数据进行广义S变换，划定噪声区域，进行主频频点的时频-分析。

4)对时频分析数据进行分析，选取动态阈值，选择数据稳定区间。波动较大数据进行滤波处理，以保留有效信号。

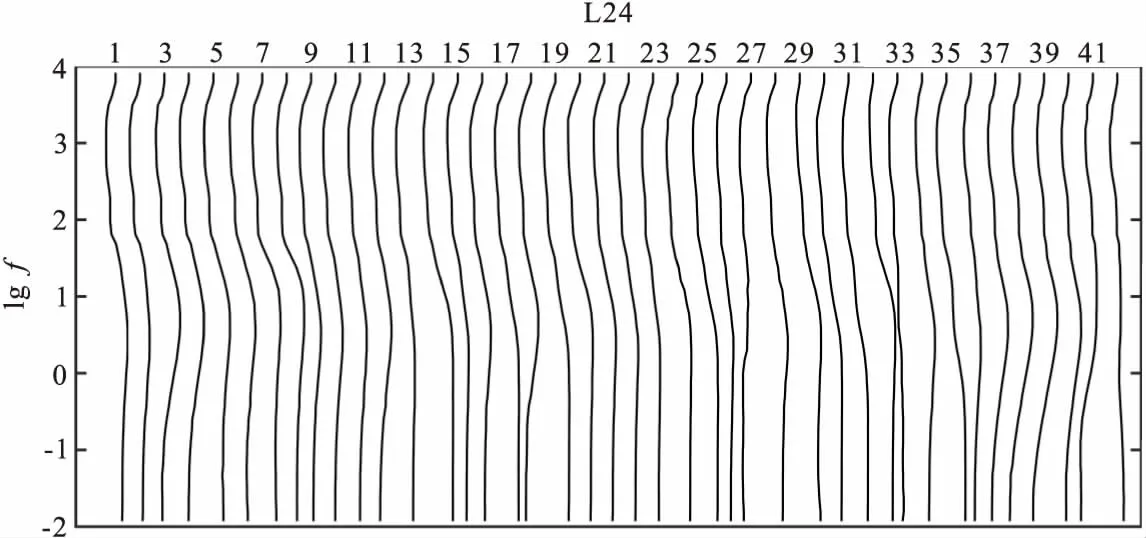
图3 某工区的视电阻率测深曲线图Fig.3 Resistivity sounding curves

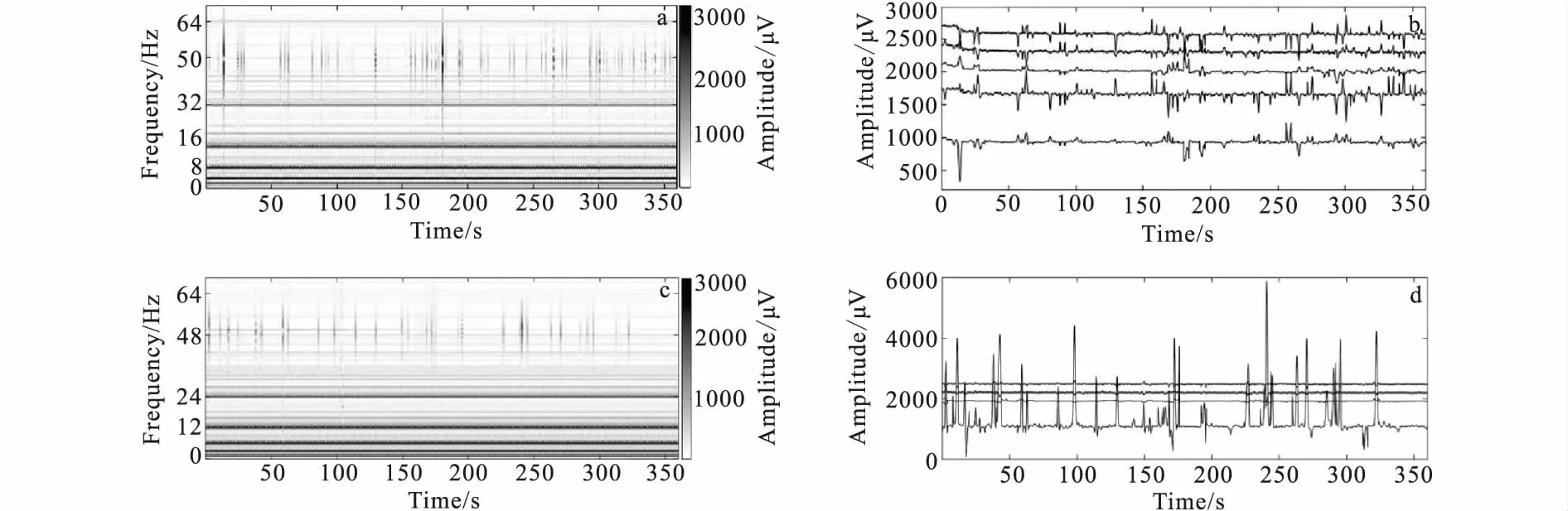
图4 高信噪比实测资料的广义S变换分析Fig.4 Analysis of the measured data of the generalized S transform(a)2频组信号1 Hz～64 Hz的S变换谱；(b)由上至下为4 Hz、2 Hz、1 Hz、32 Hz、64 Hz的幅值-时间图；(c)3频组信号0.75 Hz～48 Hz的S变换谱；(d)由上至下为3 Hz、1.5 Hz、0.75 Hz、48 Hz的信号幅值-时间图

图5 广义S变换与广域电磁法原处理效果对比Fig.5 The effect of generalized S transform is compared with the original processing method(a)信号48 Hz选取有效区间示意图；(b)通过数据矫正后广义S变换和原处理手段的电场曲线图

4 实测资料的处理效果与分析

4.1 高信噪比广域电磁数据处理

利用广义S变换数据分析处理流程,对实测的高信噪比的广域电磁数据进行处理和分析。选取的是广域电磁法某工区的高信噪比的实际测量点，工区的广域视电阻率测深曲线如图3所示，测深曲线光滑，与相邻测点具有良好的一致性，数据质量可靠。本文选取的是第8个测点的数据作为分析。

广域电磁数据发送的信号有6个频组(0频组～5频组)，一个频组包含多个频率信息。本文选取其中2频组和3频组(其中主要分析频率为0.75 Hz～64 Hz)作分析，处理的信号为电场信号，广义S变换时频分析结果如图4。实测的数据通过广域电磁法数据分析处理流程，进行数据处理得到的效果如图5所示。

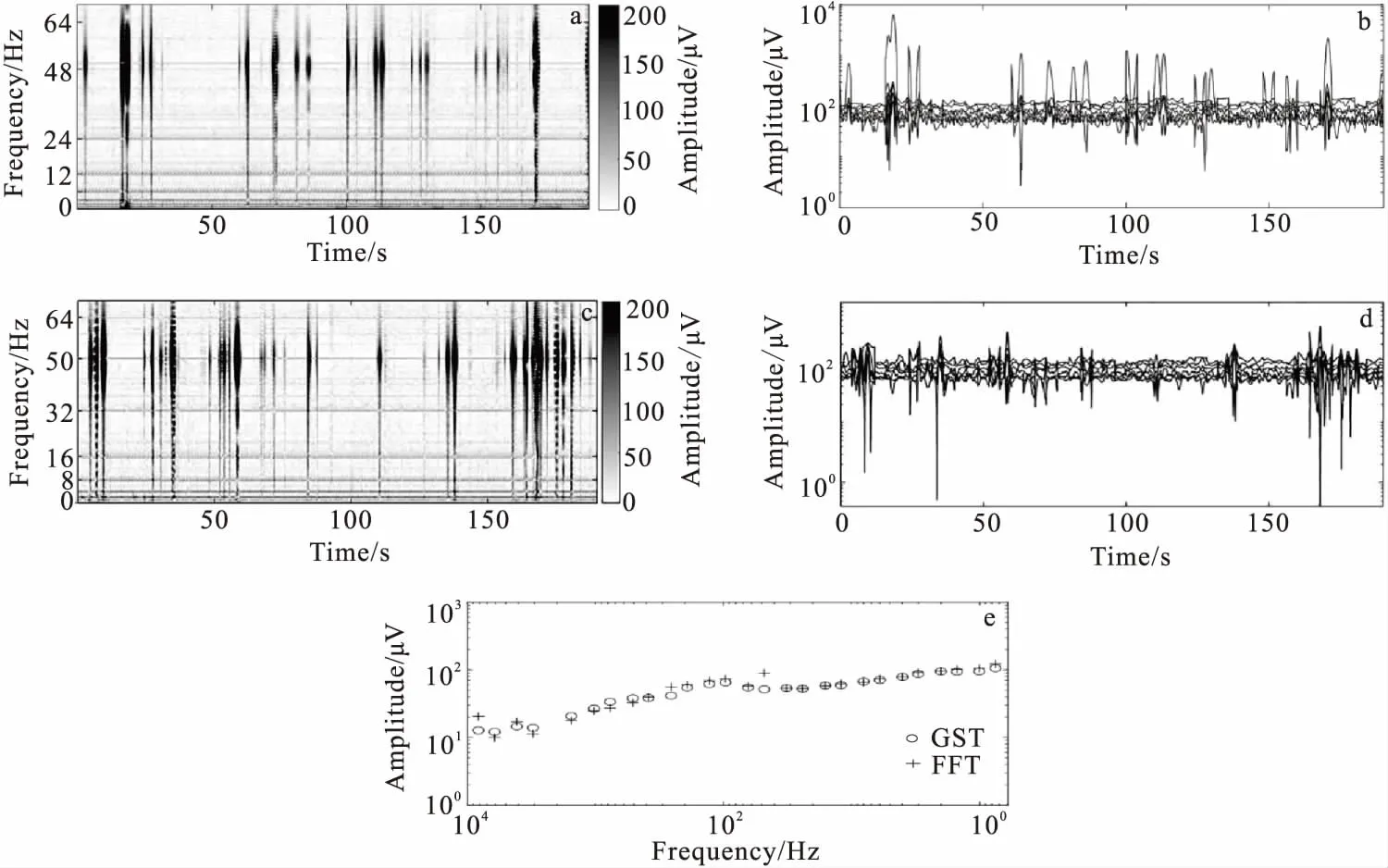
图6 实测资料干扰较大的广义S变换处与广域电磁法原处理效果对比Fig.6 Comparison of generalized S transform and original effect(a)2频组广义S变换谱；(b)(a)中信号幅值-时间图；(c)3频组广义S变换谱；(d)(c)中信号幅值-时间图；(e)原处理手段和广义S变换处理电场曲线

由图5(a)可见，在噪声干扰下，大部分时间区域幅值数据发生了波动。按流程划定噪声点选取合适时间段进行处理，能有效提高数据的质量(图5(a)中虚线框)。图5(b)为高信噪比数据经过广义S变换和基于傅里叶变换的原处理手段的效果对比。图5(b)显示广义S变换方法处理的结果同原处理手段的结果相比一致性高，证实了本方法的正确性。对比结果还表明，广义S变换时频-分析能反映幅值在时间上的变化情况，能避开噪声干扰区域、提高数据质量。

4.2 强干扰广域电磁数据处理

图6为某工区的较强干扰的广域电磁法的数据，主要分析了其180 s的电场数据，提取出对应主频频率的电场信息(0.75 Hz到8 192 Hz)。由图6(a)、图6(c)可知，以50 Hz工频干扰为中心的区域噪声对数据影响比较大，图6(b)、图6(d)中明显看出，目的主频信号在对应干扰区波动比较大，所以在处理数据时要尽量避免选取这些区域的数据。

电场数据经过本文提出的处理流程而获得图6(e)的电场曲线图。对比图6中两方法的效果能看出广义S变换获得的电场数据曲线更平滑、更稳定，得到的效果更好。证明了在干扰较强地区，选取有效的处理信号区间是十分重要的。广义S变换这种划定噪声区间提高数据质量的方法，应用到实际资料处理当中是很适合的。

5 结论与讨论

1)广义S变换不仅可以提供更多的频谱系数，还能形象呈现广域电磁主频率点幅值实时变化信息。

2)针对广域电磁时间数据，广义S变换可以圈定噪声在时频面上的分布特征，避开干扰区域为获得有效信息提供依据。

3)根据本文数据分析流程，实际处理后的数据效果更好，稳定性佳。

尽管广义S变化被众多的学者进行讨论分析，应用到实际中去，但本身并不能达到理想时频-表达ITFR的这种形式。因此，通过别的方式增加广义S变换能量聚集能力逼近ITFR有待进一步的研究。