井地2.5维DC反演研究

付德俊

(广东核力工程勘察院， 广州 510800)

0 引言

直流电阻率法(DC)是利用地下介质的电阻率参数来实现对地下地质结构的分辨和研究，该方法被广泛应用到环境与工程勘察中，其已成为目前常用的物探方法之一。

常规直流电阻率法将观测电极布设在地表，来观测地表电位的变化，并采用特定观测装置来刻画出需要的参数(如视电阻率等)，显示出地下地质体在水平或垂直方向存在电性差异，从而实现对地质体的定性分析。但是，对于特殊地质情况，地表观测到电位或视电阻率数据很难对深部地质体进行约束，较难地刻画地下地质体的边界范围，无法满足中深部工程勘察需求，为了弥补这一缺陷，开展井地直流电阻率法反演成像研究具有重要的研究意义，其弥补了纵向上深部数据对地下地质体约束。

井地直流电阻率常用的观测装置可以分为井-地、地-井-地、井-井以及井-地-井等，为了研究不同观测装置对地下地质体的分辨能力，具有重要意义。目前，国内、外研究学者进行很多相关的研究工作，Zhou等[1-2]采用解析偏导数矩阵完成了2D/3D井间DC快速成像研究；Wikinson等[3]重点分析了矿井DC反演成像技术的研究工作；国内学者同样在这方面做了大量的研究工作；王志刚等[4-6]实现积分方程法的Born 近似井地DC三维快速成像研究；吕玉增等[7]实现了井间三维直接成像研究；岳建华等[8]开展了巷道井地DC快速成像研究；徐凯军等[9]开展了基于共轭梯度算法的三维井地电阻率成像研究；蓝泽鸾等[10]开展了基于TV约束的2.5维井地直流电阻率反演研究。

笔者采用变分原理推导2.5维井地DC满足边值问题，构建了基于二阶最大平滑因子的井地DC正则化反演目标函数，采用共轭梯度算法实现了该目标函数最优化求解，最终完成不同观测方式的井地2.5维直流电阻率稳定、高效的反演研究。研究结果表明，不同观测方式的反演对异常体的约束存在明显的差异，靠近井所在的位置对异常体的约束较为明显，但是若没有地表数据的约束可能出现对异常体过渡约束，使异常体的范围出现明显的偏差。

1 井地2.5维直流电阻率正演

1.1 边值问题

在波数域，井地2.5维DC满足的边值问题[11]如式(1)所示。

(1)

式中:区域Ω为二维研究区域；Γs、Γ∞是二维区域的边界，Γs为区域Ω的地表边界，Γ∞为区域Ω的地下边界；σ为电导率；r为点电源到边界的距离；n为无穷远边界的外法向方向；k为波数；K0、K1分别为零阶、一阶第二类贝塞尔函数。

将公式(1)转化为变分问题：

Iδ(A)U]dΩ+

(2)

对计算区离散、构造插值函数，式(2)离散为：

(3)

其中，P为除供电点为0.5以外全为零的列向量。

对式(3)求变分并令其为零，得到线性方程组

KU=P

(4)

通过求解线性式(4)，得到波数域的电位U，然后通过傅氏反变换得到电位：

(5)

式中:r为点的位置；km是波数；gm是加权系数[11]。

表1 傅氏变换系数km和gm

1.2 2.5维井地DC观测方式

常用的井地DC观测装置可以分解成一下四种：①井-地；②地-井-地；③井-地-井；④井-井测量装置，其野外布置方式图1所示。

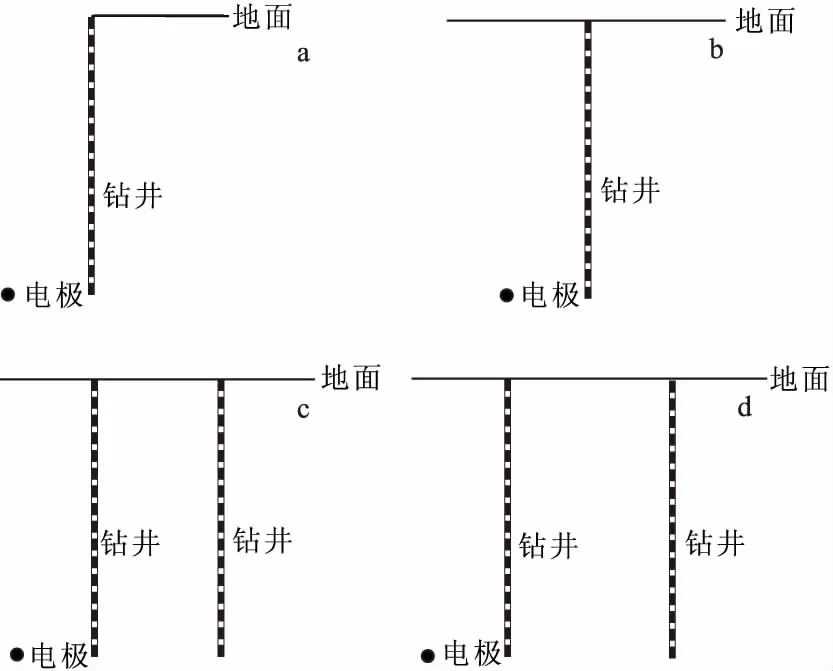
图1 2.5维井地DC观测装置示意图Fig.1 Schematic diagram of2.5-D well ground DC observation device(a)井-地;(b)地-井-地; (c)井-地-井;(d)井-井

2 共轭梯度正则化反演

构建正则化反演目标函数[12]：

φ(m,α)=φd(m)+αφm(m)

(6)

其中：φ(m,α)为构建的正则化目标函数；α是正则化因子；φd(m)为数据约束项；φm(m)为模型约束项；m为模型参数。数据约束项与模型约束项表达式分别为：

φd(m)=Wd(A(m)-dobs)TWd(A(m)-dobs)

φm(m)= (m-mapr)T(m-mapr)

(7)

其中：A表示为正演算子；dobs表示为观测数据；mapr为已知地下结构的先验信息；Wd为数据权重矩阵。为了获得最优的解，必须对正则化目标函数求最小，即

φ(m,α)=φd(m)+αφm(m)→min

(8)

笔者采用共轭梯度算法求解公式的最优化问题，其采用的基本思想为最速下降法[13]：

mn+1=mn+Δm

(9)

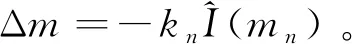
初始梯度迭代向量表达式为：

(10)

首次迭代方向为梯度向量与首次迭代共轭梯度向量的线性组合

(11)

第n+1次迭代的方法为：

(12)

采用线性搜索求解目标函数最小来获取最速下降迭代步长：

(13)

通过简化，可获取到下降步长为式(14)。

(14)

3 算例分析

3.1 算法验证

图2展示了电导率为0.01 s/m均匀半空间的理论电位曲线与数值模拟的电位曲线对比图，相对误差范围在2%以内,对比结果表明本文正演算法正确可靠。

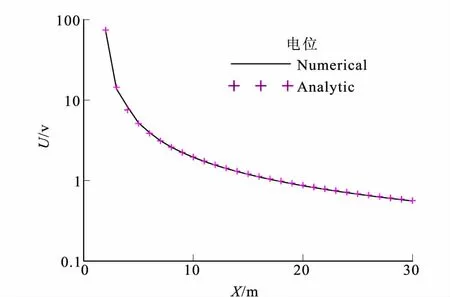
图2 数值解与解析解电位对比曲线图Fig.2 Comparision of FEM numerical and one- dimensional analytical solutions

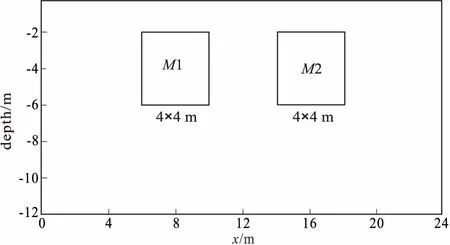
图3 地电模型断面图Fig.3 Sectional view of the electric model

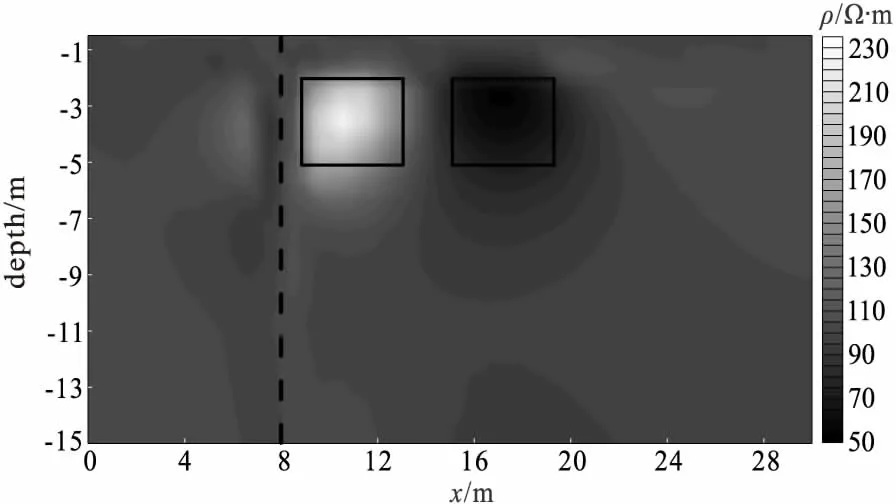
图4 井-地反演断面图Fig.4 Sketch map of borehole-surface dc resistivity

图5 地-井-地反演断面图Fig.5 Sketch map of surface-borehole- surface dc resistivity

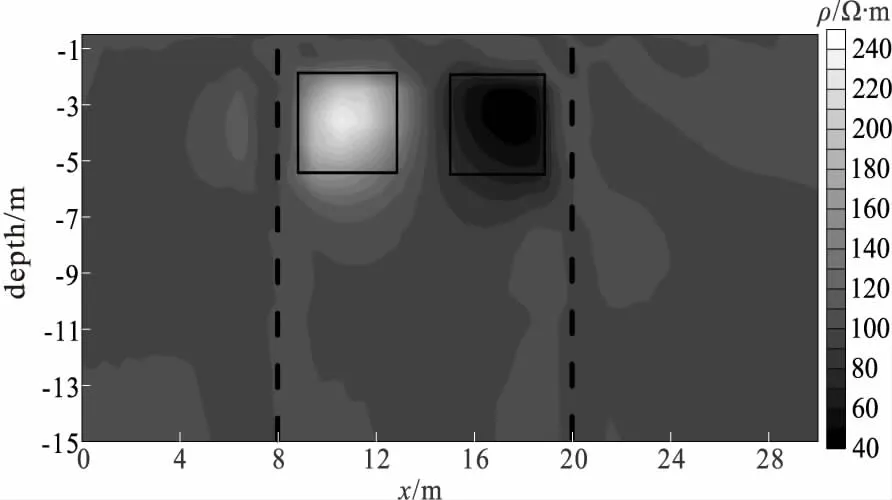
图6 井-地-井反演断面图Fig.6 Sketch map of well - to - well dc resistivity

图7 井-井反演断面图Fig.7 Sketch map ofcrosshole dc resistivity

3.2 不同观测方式反演对比分析

图3为地电模型，均匀半空间下存在埋深以及大小相同而不同电导率的两个异常体，异常体1的电导率为0.005 s/m ，异常体2的电导率为0.02 s/m，背景电导率为0.01 s/m，异常体尺寸为4 m×4 m，异常体的顶部埋深为2 m，设计了如上所述的四种井地直流电阻率的观测方式，图(4)～图(7)的虚线表示井设计的位置。理论正演得到的合成数据(直接采用观测电位作为数据来源)加入3%的高斯白噪声后作为反演输入数据，此次反演网格与正演网格一致，网格大小为42×20，并向外进行了网格延拓以降低截断边界带来的数值误差。采用Pole-Pole采集装置，对于井-地测量方式总电极数为20个，地表布设12个，井中布设8个；地-井-地测量方式总电极数为24个，地表布设16个，井中布设8个；井-地-井测量方式总电极数为32个，地表布设16个，井中布设16个；井-井测量方式总电极数为16个，地表布设0个，井中布设16个。最后采用共轭梯度法实现了不同观测装置的井地电阻率2.5维二阶平滑模型正则化反演研究。

图4～图7分别展示了井-地、地-井-地、井-地-井以及井-井四种观测方式的反演结果。此次反演最大迭代次数为20次，图8、图9分别展示数据误差与迭代次数的衰减图以及正则化因子α与迭代次数的变化曲线。从反演结果中可以看出，反演结果都能够较好体现异常所在的位置，反演结果较为明显。但是对于不同观测方式其反演结果得到细节不一样，对异常体边界的识别程度不一致。从图4的反演结果可以看出，靠井所在位置的异常体，其反演的结果呈现的范围更加集中，而远离井的异常体反映的区域相对较大。图5展示了地-井-地的观测装置的反演结果，当井位于两个异常体的中间时，井所采集的数据对两个异常体都存在约束，两个异常体都能较为明显分辨。对比图4～图5可发现，地-井-地的观测方式相对井-地方式提高提高了异常体的分辨率，其对井旁左右的异常体都有较好地约束，而井-地观测方式对靠近井的异常体约束权重相对大。

图6井-地-井观测方式的反演结果表明，异常体的边界相对前两种的反演结果更为集中，反演的结果与实际模型的吻合度高，反演得到的电阻率值与真实电阻率值相差不大。图7的井-井观测方式的反演结果表明，其反演得到的异常体范围与真实结果相差较大，由于缺乏地表数据的约束导致异常反演趋向井所在的位置，井附近的细节较为明显，总体上异常体相应位置得到体现。从图6～图7的对比发现，地表观测数据能够较为全面进行约束，避免了过渡依赖井中数据，避免假异常的存在。

综合分析图4～图7的结果可以表明，井中数据能够较好弥补地表观测数据对纵向约束减弱的缺陷，同时能够提高反演非唯一性。从反演的结果表明，井-地-井的观测方式对异常体的边界圈定相对其他三种观测方式较好，但是存在一些小的细节异常，地-井-地观测方式能够较好对井两旁异常体都有较好的约束效果，而远离井的异常体其约束能力逐渐降低，这一现象在井-地测量方式得到体现。

图8、图9分别展示了数据误差随迭代次数的增加而逐渐减小，正则化因子α随迭代次数的增加而逐渐减小的这一规律。当模型达到一定时，即随着迭代次数的增加人为的减少模型约束权重，使反演结果更加倾向对数据的拟合来降低反演的数据误差，最终达到稳定的反演结果。

4 结论

不同观测方式的井地电阻率2.5维共轭梯度反演结果表明，我们开发的算法正确可靠，反演算法稳定高效。根据以上的研究可以得出以下几点认识：

1)井中数据能够较好弥补地表观测数据对纵向约束减弱的缺陷，能够有效地降低反演非唯一性，同时井-地-井观测方式所采用电极数量大于其他观测方式，其获得的地下异常体信息较为丰富，其反演的异常范围更为集中，其对异常体的圈定要优于其他观测方式。

图8 数据误差与迭代次数曲线图Fig.8 Curve of between iterationserror and iterations

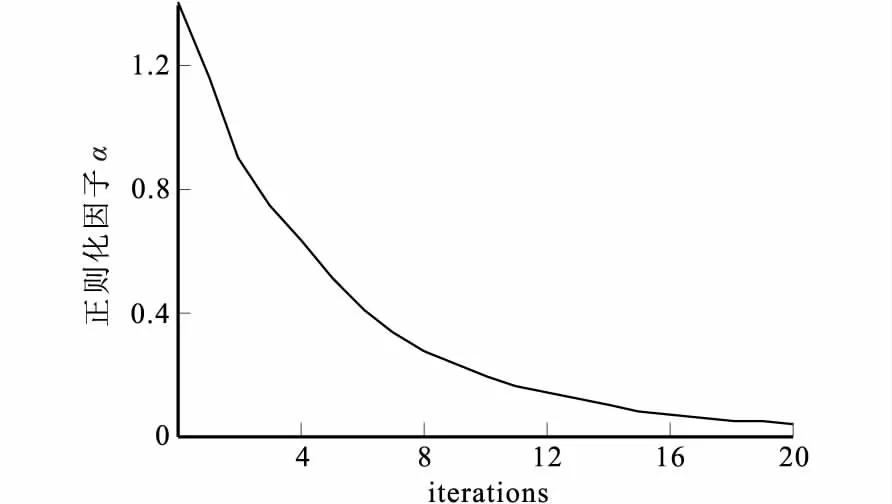
图9 正则化因子α与迭代次数变化曲线图Fig.9 The graph of the change of regularization factor and iteration number

2)由于地表测量电极的缺失，导致井-井观测方式在横向上对异常体的约束减少，数据量的减少很大程度上增加反演的非唯一性，导致反演精度差，使得井的左右两侧出现假异常，但也能大致地反应异常的范围，能够给实际情况提供参考。

3)基于平滑约束的二阶最大平滑稳定因子的共轭梯度法迭代反演方法，能够较为稳定获取反演结果，同时模型约束项增加提高反演的稳定性，其为后期开发更为稳定模型约束项提供借鉴。