海洋可控源电磁法多参数正演响应特征分析
兰怀慷,熊 彬,罗天涯,黄业中,梁 卓,李祖强,唐 杰
(1.桂林理工大学 地球科学学院,桂林 541006;2.防城港市国土资源局,防城港 538001)
0 引言
地球上海洋面积达到3.6亿多平方公里,约占地球总面积的71%,在人类面临人口剧增、资源匮乏的当今,开发利用海洋是解决这一难题的有效途径之一,21世纪将是人类开发利用海洋的世纪[1-4],是“海洋开发的时代”。随着海洋CSEM对海洋地质构造调查、油气储层预测、固体矿产探测及海底工程勘查等的大量需求,国内、外学者均加大了对于海洋CSEM探测方法的数值模拟研究和试验分析力度。Cox[5-6]首次在浅水域环境下进行了水平电偶极子CSEM研究且进行了试验,此种方法在海底发送电偶极子信号,并在各测点接收海洋地层和海水层的电场响应。CSEM电磁场相对于天然场高频部分不会被海水屏蔽,对海底浅部有较高的分辨率,因此广泛应用于海洋岩石圈研究、洋中脊研究以及海底天然气水合物研究[7-9]。随着海洋CSEM数据采集技术和数值计算方法的高速发展,CSEM在石油勘探方面取得了长足的发展[10-12]。选取合适的频率和偏移距对高阻层的探测是非常关键的,观测垂直电场Ez和水平磁场分量Hx可以带来海底高阻层更多的信息,须指出的是,在浅海水环境中测量垂直电场Ez是有益的。
在大多数的数值模拟中,常常假定介质是线性的、各向同性的,介质的介电常数ε、磁导率μ、电导率σ与时间、温度、压力等无关;介质的磁导率等于真空中的磁导率μ。严格地说,描写介质电磁性质的参数ε、μ、σ不一定是常数。不仅因时间、空间而变化,还因物质成分、温度、压力、频率等而变,正是如此,基于海洋电磁法多参数正演响应研究是很有必要的。笔者讨论了海洋CSEM勘探受到多个因素影响,如海水深度、海底目标层电阻率、磁导率、介电常数、地层厚度等变化时的电磁场响应。总结这些因素与响应结果之间的影响规律,并提出一些新认识,这对今后实际资料的处理、反演、解释有一定的借鉴。
1 水平电性源频率域电磁响应
1.1 长导线源海水层中电磁场的解
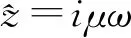
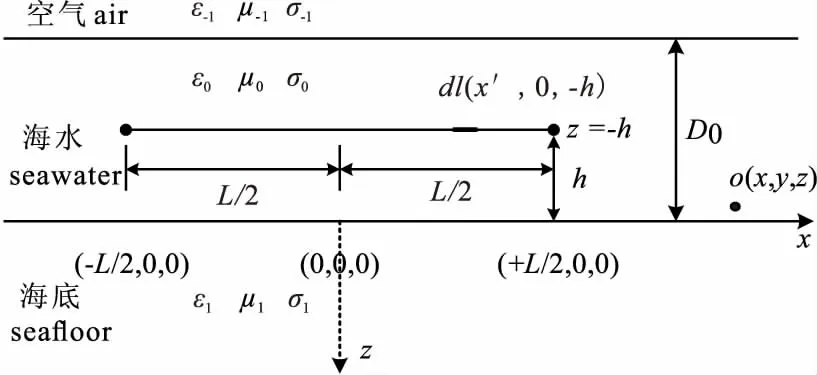
图1 海底长导线源示意图Fig.1 The schematic diagram of long wire source at the bottom of the sea
将发射源作为偶极子进行处理时,可以大大简化电磁场的求解,但这只适用于大偏移距,当偏移距较小时,计算结果存在较大误差。因此有必要求解长导线源的电磁场。建立图1所示直角坐标系,设长导线源的长度为L,位于海底z=-h,选取电偶源中点在海底的投影为坐标原点,x轴与偶极矩方向一致,z轴垂直向下。根据电磁场的可叠加性原理,该长导线源产生的电磁场等于单位长度电偶极子产生的电磁场沿导线长度的线积分。首先,对长导线进行剖分,根据电偶源的电磁场表达式,写出位于x轴x'处的任意线元的电磁场表达式,然后[-L/2,L/2]在范围内对变量积分,得到长导线源的电磁场公式如下:
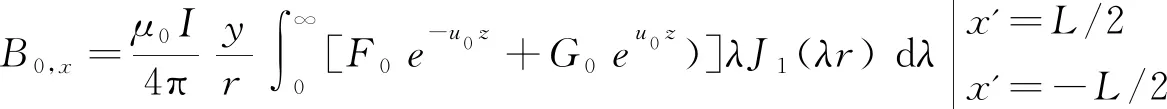
(1)
(2)
(3)
(4)
(5)
(6)
(7)
(8)
1.2 常用数值滤波算法
针对式(1)中的Hankel积分,对比研究了五套数字滤波的快速汉克尔变换算法(Anderson,1979,1982,1989,1991;Johansen and Sorensen,1979;Kong,2007;Guptasarma and Singh,1997)[14-17]的计算精度。选用常用的存在解析解的汉克尔数值积分来对比分析:
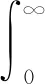
(9)
图2和图3分别是Hankel零阶滤波系数的数值解与解析解对比曲线及其相对误差曲线,积分函数自变量取r=0.01~5.0。结果表明,五套数字滤波的快速汉克尔变换算法在逼近相应的理论解析解时,均不存在振荡现象,且计算精度高[18]。从整体上看,滤波方法计算精度从高到低,依次为Kong241、 Kong121、Anderson801、G&S120、Johanson200;其中Kong241计算精度约 数量级,其余四套滤波计算精度都低于Kong241;这表明Kong241滤波方法具有较高的稳定性。因而文中采用Kong241对上述Hankel积分进行求解。
2 数值算例
如图4所示的观测系统:发射源为水平电性源长度L=300 m,距离海底高度h=30 m,频率f=0.25 Hz;观测点x在0 m~15 000 m,采样点个数为200,y在0 m~2000 m,z=-0.5 m。以下算例中不特殊指出均用以上装置参数和表1给出的地电模型参数。
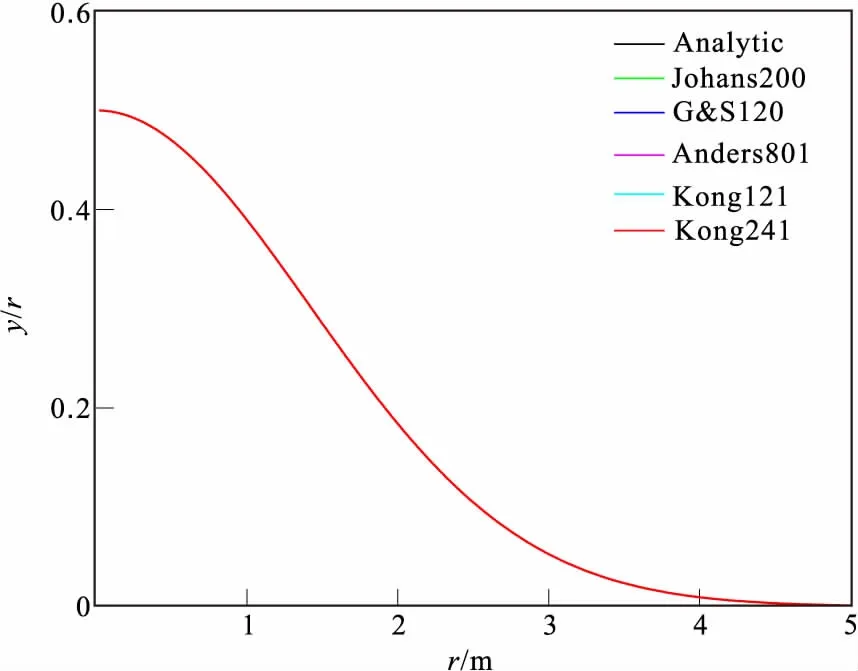
图2 数值解与解析解的对比Fig.2 Compared with analytical solution of numerical calculation
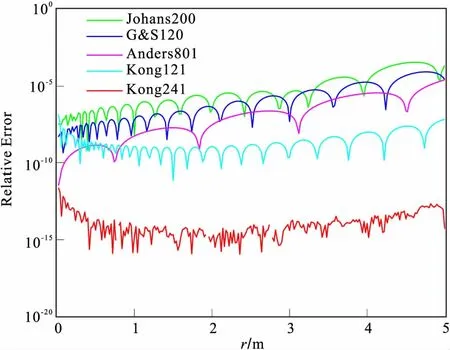
图3 数值解与解析解的相对误差曲线Fig.3 The relative error curve of numerical solution with analytical solution
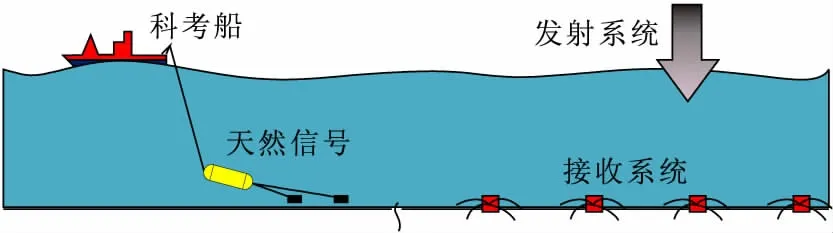
图4 CSEM 探测示意图Fig.4 The schematic diagram of CSEM detection
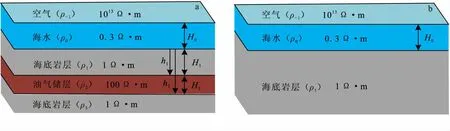
图5 经典一维海洋地电模型Fig.5 The canonical 1D ocean model(a)海底岩层含高阻层;(b)海底岩层为均匀半空间
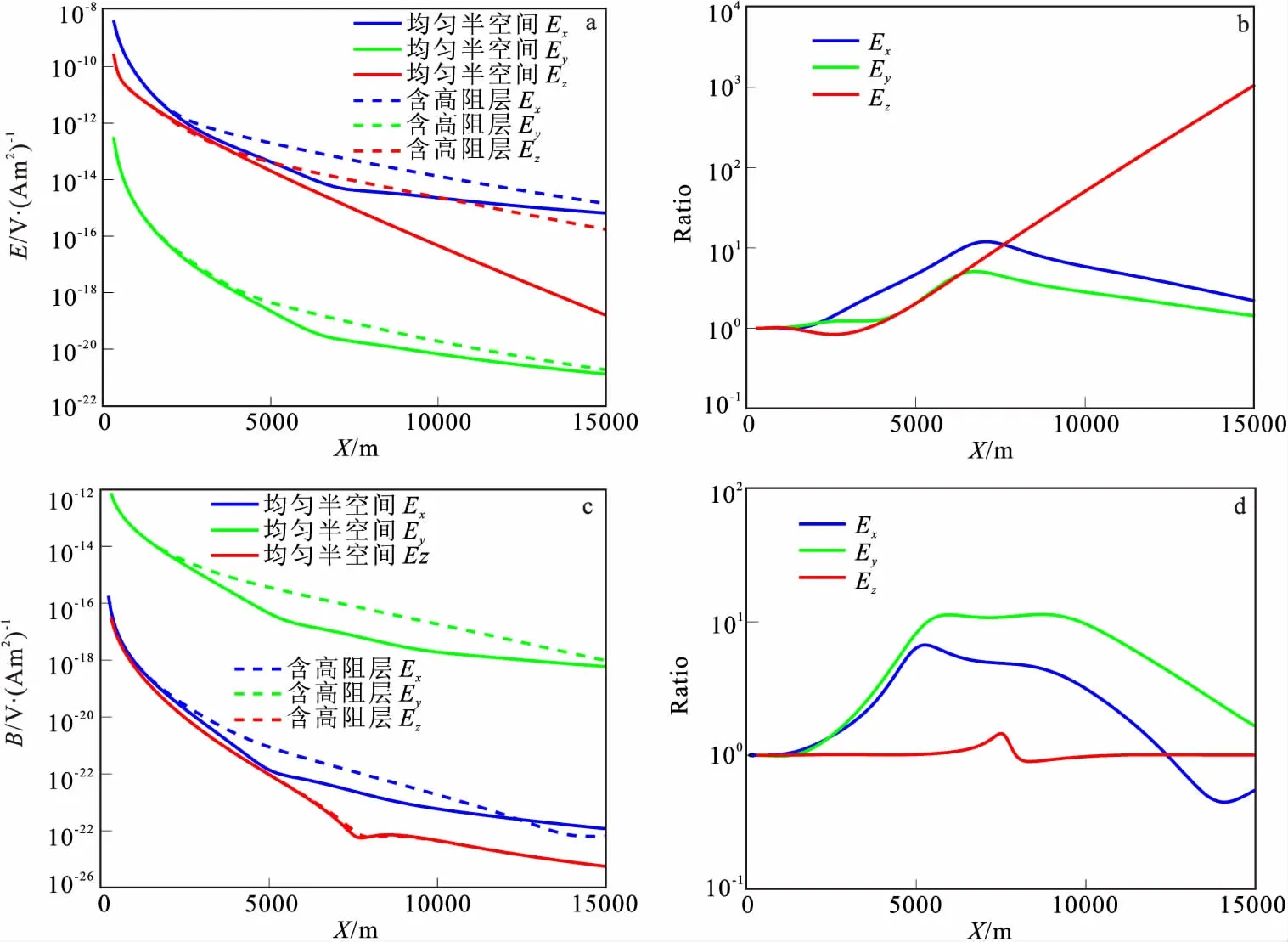
图6 主测线经典海洋模型电磁场响应曲线及其比值Fig.6 The electromagnetic response curve and its ratio of the canonical ocean model(a)电场分量;(b)电场分量比值;(c)磁场分量;(d)磁场分量比值
2.1 不同电磁分量分析
由于海水的温度和含盐度比较稳定(除了地中海和地球两极附近),因此,可以认为海水的电导率是稳定的(在3 S/m~5 S/m范围内)。海壳与陆壳相比,有很多不同的特点,尤其是在导电性上。因为海底岩层高的孔隙度和渗透性,所以几乎所有的海洋地壳上部实际上是海水饱和的,特别是海底的第一层、第二层(海底沉积物和枕状玄武岩),使得海底岩层不像陆地那样近地表小范围内往往存在导电不均匀性,也不再像陆地那样岩石成分是其导电性的主宰因素。相反,岩层的孔隙度和充填其中的介质决定了海洋地壳导电性,因此,海洋海底沉积物的电阻率一般较低,变化范围也不大。
如图5所示的海洋地电模型,按照表1给出的参数取值,根据第二节中给出的公式计算两种模型下电磁响应如图6所示。由图6(a)和图6(c)可以看到,电磁场各分量幅值均随着偏移距x的增大而逐渐减小,减小的幅度越来越小;含高阻层地电模型电磁场(除y方向磁场分量By大偏移距外)各分量(虚线)的幅值均比均匀半空间地电模型电磁场各分量(实线)的幅值均大,电场y分量比x和z分量幅值小4个数量级,而磁场分量比和分量幅值大4个数量级。图6(b)表明,电场各分量中垂直分量Ez的比值在探测区间内随偏移距增大而逐渐增大,水平分量Ex和Ey,比值随偏移距增大呈现先增后减的趋势,并且在较大偏移距时比值趋于1,高阻层引起的异常逐渐不明显。图6(d)表明,在磁场各分量中水平分量By和Bz异常随偏移距增大先增后减,y分量异常幅值更加明显,而垂直Ez分量这只有在偏移距x=7 000 m~8 000 m处存在较小异常。且在较小偏移距x<3 000 m时,海底高阻层引起的异常均不明显。综上所述,Ez和Ey对海底高阻层的探测更加有益。
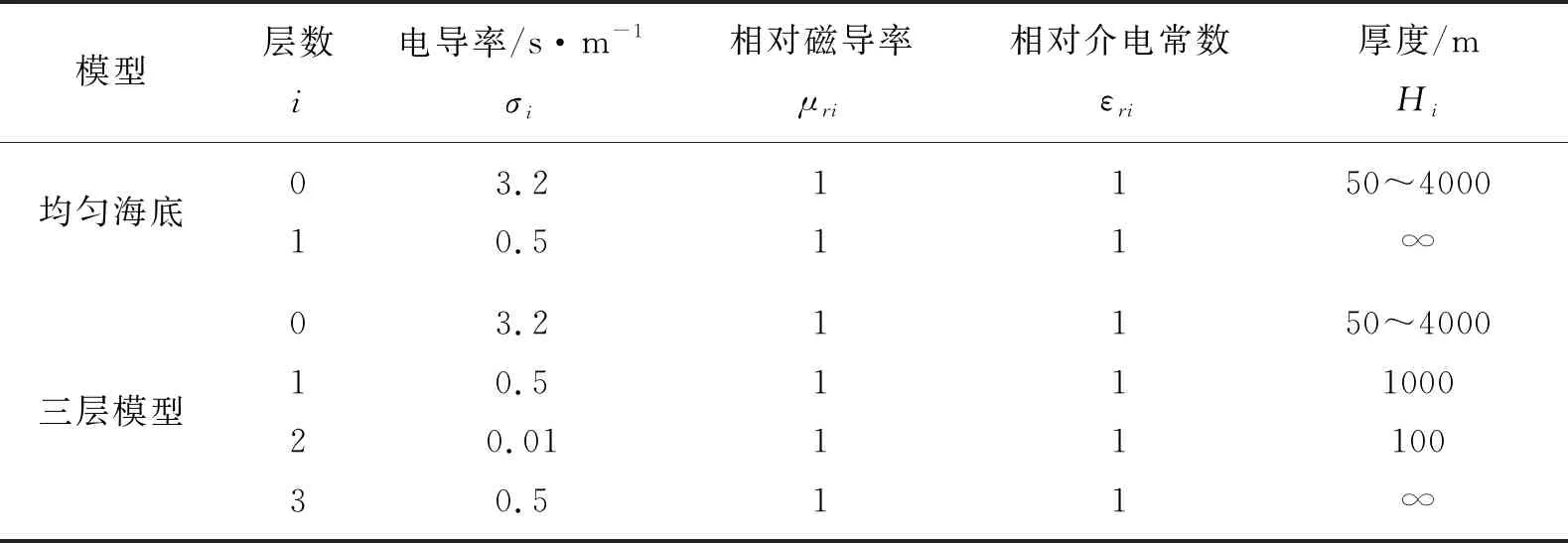
表1 海洋地电模型参
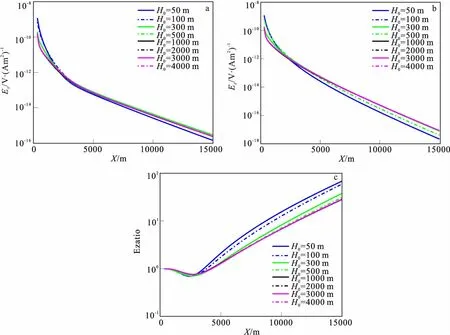
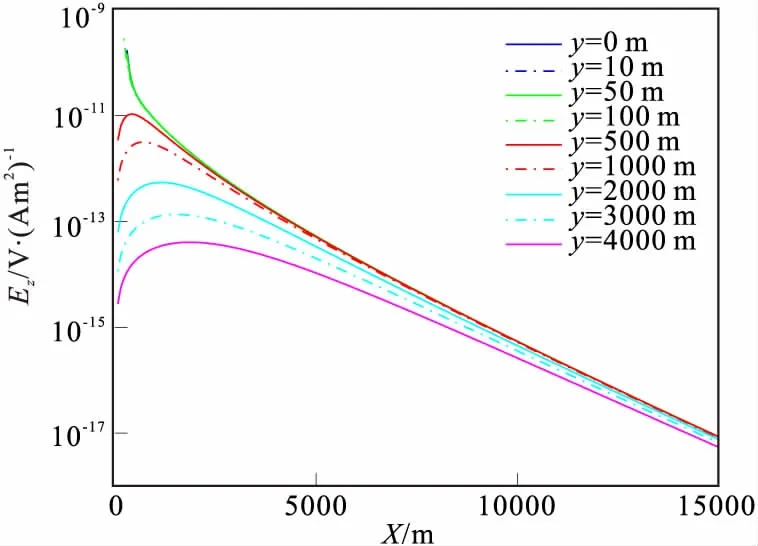
图7 不同海水深度时的电场分量Fig.7 The vertical component of electric field in different seawater depth(a)均匀海底的电场分量;(b)含高阻层的电场分量;(c)高阻层引起的相对异常
2.2 海水深度变化的电磁响应
为了考察空气波对电磁场的影响与海水深度的关系,设海水厚度H0在50 m~4 000 m之间变化,分别计算了不同海水深度时,海底均匀半空间和海底三层地电模型的电场Ez分量和磁场Bx分量的幅值和相对异常(图7、图8)。从图7(a)、图7(b)可知,无论海底是否含有高阻层,Ez分量与海水深度H0正相关,随着x增大其幅值差异变大。
图8(a)、图8(b)表明,分量幅值大小与海水深度反相关。图7(c)和图6(c)为高阻层引起的相对异常(海底岩层含高阻层时与海底为均匀半空间的电磁响应比值),从图7(c)可知,水深从50 m~4 000 m变化时,随着偏移距的增大,异常的差异逐渐增大。同时可以发现,海水深度越小Ez相对异常越强,对高阻层的探测能力越好。但是,较小偏移距时,异常曲线幅值趋于1,表明小偏移距时探测能力较差。因此,根据地质资料设计合适的偏移距对野外测量有重要的指导意义。
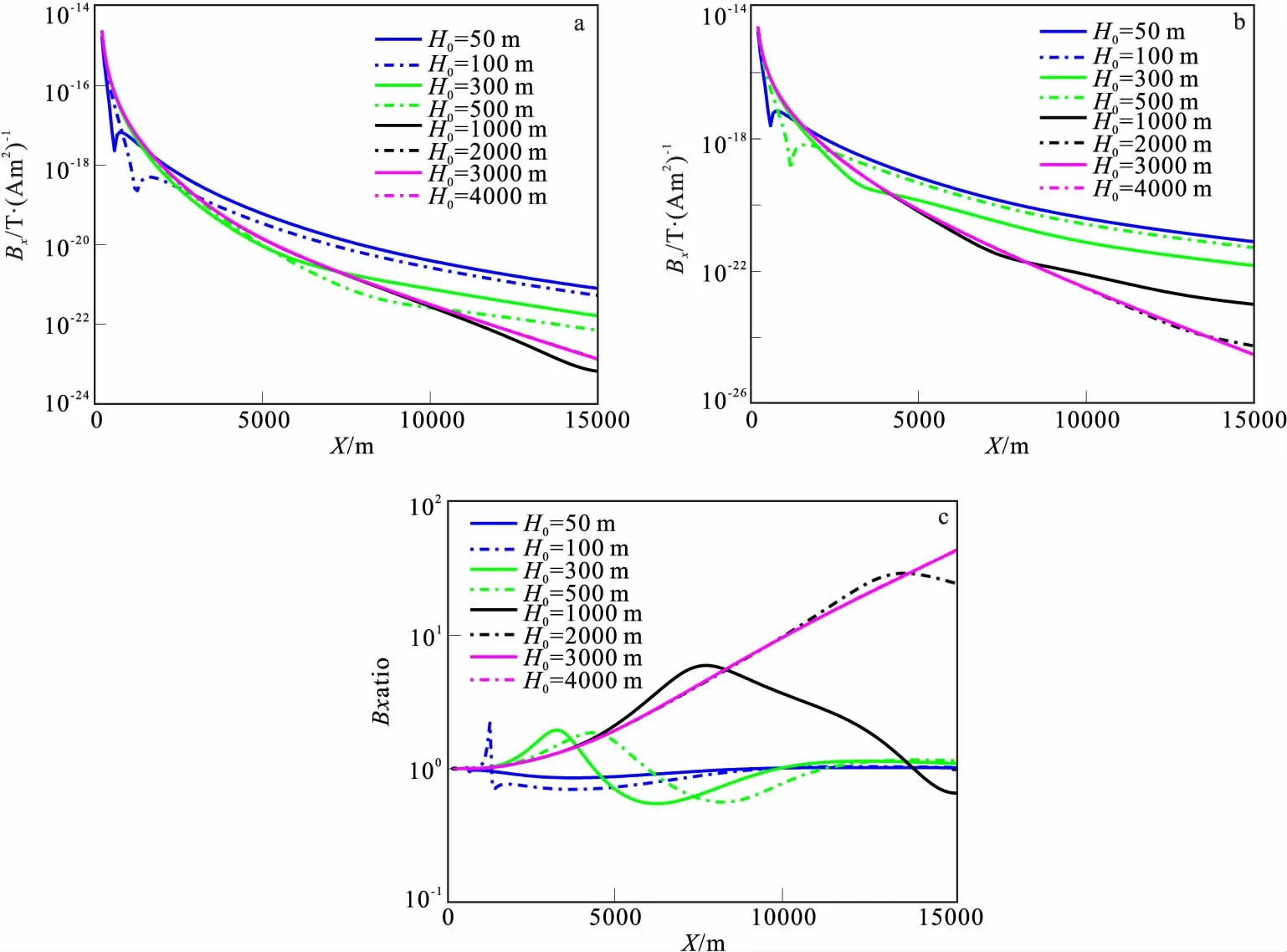
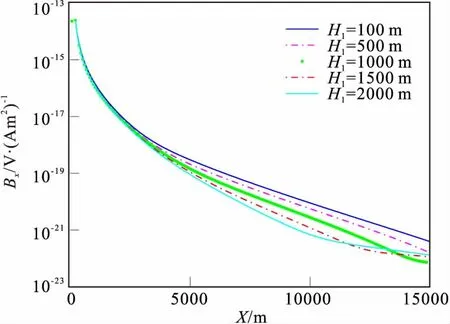
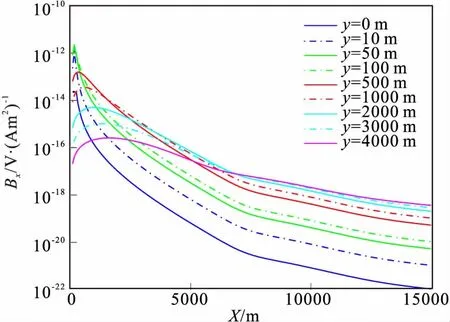
图8 不同海水深度时的磁场分量Fig.8 The horizontal component of magnetic field of different water depth(a)均匀海底的磁场分量;(b)含高阻层的磁场分量;(c)高阻层引起的相对异常
从图8(c)可知,海水深度H0小于500 m时,在观测偏移距范围内磁场Bx分量相对异常值不大,变化没有Ez分量那么明显;H0>1 000 m时,异常较为突出,且存在一定变化规律,相对异常曲线存在极大值和极小值两个峰值,随着海水深度加大,它们极值有所增大,且向偏移距增大方向移动;当水深大于3 000 m以后,相对异常曲线在测区内变成单调性随偏移距增大而增大。总之Bx分量对高阻层探测能力在浅水区不显著,受空气波影响较大,深水区探测能力较好。
2.3 不同介电常数的电磁响应
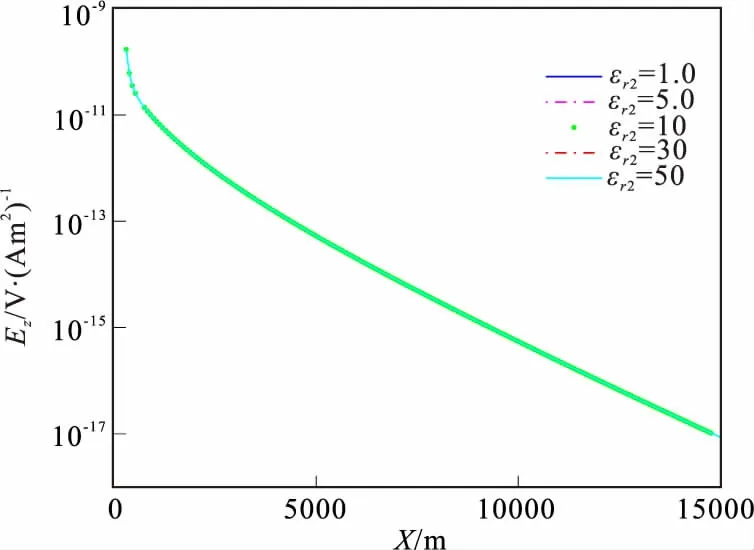
图9 不同介电常数时电场Ez分量Fig.9 The vertical component of electric field of different dielectric constant
取海水深度为H0=1 000 m,根据表1的参数计算三层模型中电磁场随相对介电常数变化的规律,其中海水层和海底第一层、第三层岩层的磁导率和介电常数分别取真空中的磁导率和介电常数,第二层岩层中磁导率取真空中的值,相对介电常数分别选取εr2=1、5、10、30、50。图9和图10分别为介质的介电常数变化时电场Ez分量和磁场Bx分量的幅值随x偏移距的变化曲线。结果表明,介质的介电常数变化时对电场Ez和磁场Bx分量的幅值基本没有影响。因此海洋可控源电磁法可以不考虑介电常数的变化。

图10 不同介电常数时磁场Bx分量Fig.10 The horizontal component of magnetic field of different dielectric constant
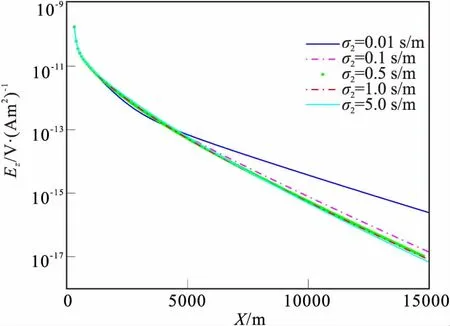
图11 不同电导率时电场Ez分量Fig.11 The vertical component of magnetic field of different electrical conductivity
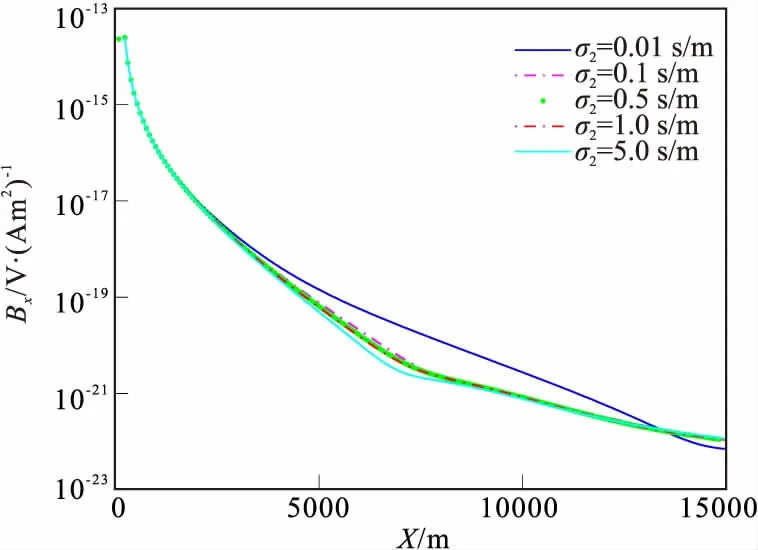
图12 不同电导率时磁场Bx分量Fig.12 The horizontal component of magnetic field of different electrical conductivity

图13 不同磁导率时电场Ez分量Fig.13 The vertical component of electric field of different magnetic permeability
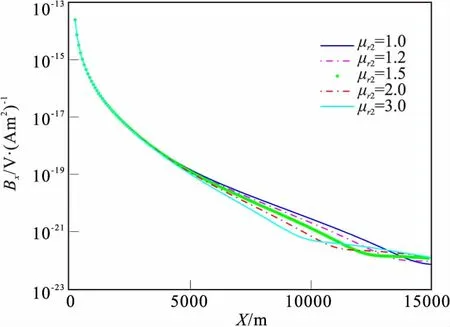
图14 不同磁导率时磁场Bx分量Fig.14 The horizontal component of magnetic field of different magnetic permeability
2.4 目标层不同电导率的电磁响应
假设目标层电导率在0.01 S/m~5.0 S/m之间变化,从图11和图12可知,在小的偏移距处(x<5 000 m),随着目标层电导率的变化,Ez分量的幅值影响不显著,x>5 000 m时,含高阻层曲线异常明显,含低阻层曲线异常不显著,表明Ez分量对高电阻层探测分辨能力显著,对低阻层探测能力较差。Ex分量,除了电导率σ2=0.01 S/m曲线外,其余曲线均逼近同一幅值,这里值得注意的是,Ez分量对高电阻层探测分辨能力显著(如σ2=0.01 S/m)曲线),然而对低阻层探测能力不明显(如σ2=2.0 S/m、5.0 S/m曲线);Bx分量在偏移距为3 000 m~12 000 m时,探测能力显著。
2.5 目标层不同磁导率的电磁响应
选取目标层的相对磁导率μr2=1、1.2、1.5、2.0和3.0。由图13和图14可得,Ez分量的幅值变化规律与海底目标层磁导率变化反相关,小偏移距(x<5 000 m)时,差异不明显;而Bx分量的幅值在适中偏移距(5 000 m 图15 目标层不同埋深时电场Ez分量Fig.15 The vertical component of electric field when the target layer buried depth are different 图16 目标层不同埋深时磁场Bx分量Fig.16 The horizontal component of magnetic field when the target layer buried depth are different 图17 目标层不同厚度时电场Ez分量Fig.17 The vertical component of electric field when the target layer have different thickness 图18 目标层不同厚度时磁场Bx分量Fig.18 The horizontal component of magnetic field when the target layer have different thickness 图19 不同旁测线电场Ez分量Fig.19 The vertical component of electric Field by the different line 图20 不同旁测线磁场Bx分量Fig.20 The horizontal component of magnetic field by the different line 假设海底目标层埋深在100 m~2 000 m变化。图15表明,偏移距一定时,电场Ez分量的幅值随着目标层埋深增大而减小,小偏移距处(x<3 000 m)Ez分量的幅值受到目标层埋深变化影响小且规律不明显;图16容易看出,适中偏移距时磁场Bx分量的幅值随着目标层埋深变化规律明显呈反相关,目标高阻层埋深越深,Bx的幅值越小。这表明了大偏移距时电场Ez分量比磁场Bx分量具有更高探测分辨能力,小偏移距时磁场分量具有更高探测分辨能力。 目标层为高阻层(σ2=0.01 S/m),假设海底目标层厚度H2在5 m~200 m之间变化。从图17容易看出,电场Ez分量的幅值受到海底目标层厚度变化而影响,主要在大偏移距期间段,当偏移距一定时,随着海底高阻目标层厚度的增加Ez分量的幅值增大,小偏移距处变化不显著。图18表明,磁场Bx分量的幅值曲线存在一个拐点,拐点位置随高阻层厚度增大向偏移距增大方向移动。 按照表1均匀海底设置参数,取旁侧距y为0 m~4 000 m变化时,图19表明,电场Ez分量的幅值与y呈反相关,随着偏移距x的正大幅值趋于一致,注意到,y<100 m时,Ez曲线与主测线一致,y>500 m时,小偏移距处存在一个极大值点。图20表明,磁场Bx分量的幅值整体与y呈正相关。因此,在进行数据分析时要充分了解各分量曲线特征,根据不同旁侧线的位置具体分析,才能得到可靠的结论。 1)电场Ez分量和磁场Bx分量受介质的介电常数变化的影响微小,海洋可控源电磁法中介质介电常数的影响可以忽略。 2)海洋可控源电磁法中电场Ez分量和磁场Bx分量对海底高阻层的探测效果明显好于对低阻层的探测,且对高阻层厚度、埋深、磁导率变化等均有良好的探测效果。 3)海洋可控源的探测效果与偏移距的选择有密切关系,综合分析,有利偏移距范围为3 000 m~12 000 m。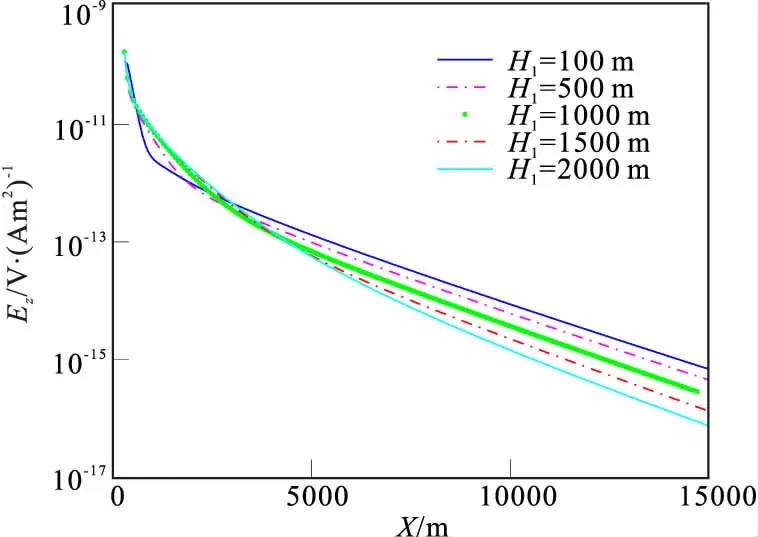
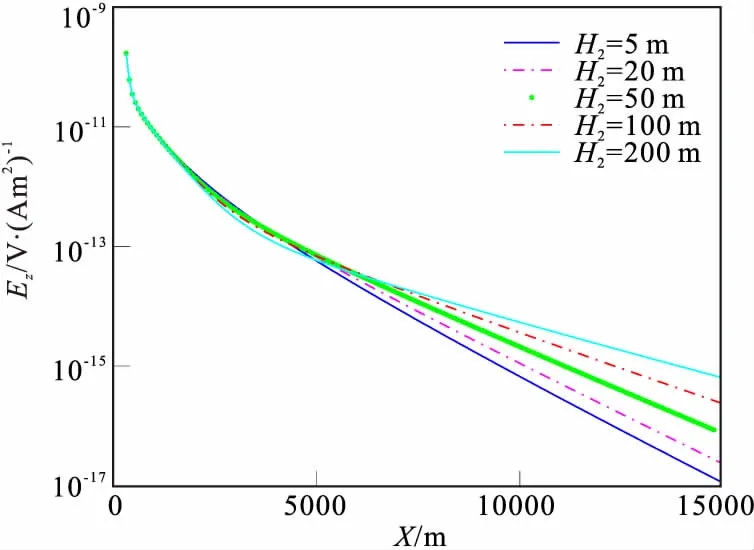
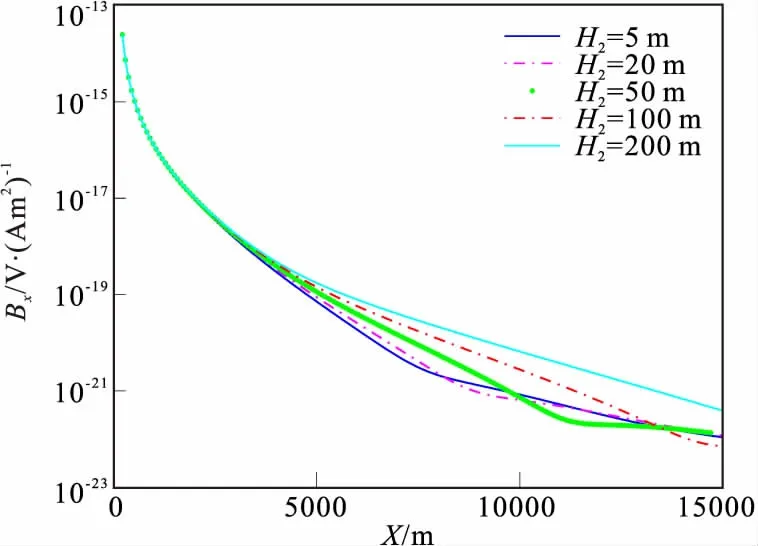
2.6 海底目标层不同埋深的电磁响应
2.7 目标层不同厚度的电磁响应
2.8 不同旁侧线的电磁响应
4 结论

