直觉模糊决策系统的知识约简*

张 炜，王加阳，帅 勇，龙陈锋

1.中南大学 信息科学与工程学院，长沙 410006

2.湖南农业大学 信息科学技术学院，长沙 410128

1 引言

粗糙集理论[1-2]由Pawlak于1982年提出，是一种处理不确定性信息的数学工具，已在机器学习、模式识别、决策分析和知识发现等领域[3-6]广泛应用。该理论的主要思想是用等价关系形成的知识粒来近似表示信息，其主要应用之一是属性约简。如，景运革等人[7]提出的知识增量属性约简算法，然而随着现实数据结构复杂化、多样化，经典粗糙集已无法满足求解需要，众多学者从不同角度出发对其进行扩展，模糊粗糙集也是其中一个重要分支。Pawlak等人在文献[8]给出了将经典粗糙集推广到模糊粗糙集的可能性。随后Mi和Sun等人[9-10]将信息表中条件属性和决策属性均模糊化处理，使得经典粗糙集中的相似关系变为模糊等价关系。文献[11-14]进一步研究了模糊粗糙集的约简，并提出了多重约简方法。然而研究发现模糊粗糙集存在缺陷：它仅用隶属度来刻画“完全肯定”的程度，缺少对“完全否定”的判断。接下来，Atanassov[15]提出用直觉模糊对模糊理论进行扩充，克服了上述缺陷。吴伟志等人[16]和苗夺谦等人[17-18]将直觉模糊理论同粗糙集结合，提出了直觉模糊粗糙集模型并给出了约简方法。

Dempster提出的证据理论[19]是处理不确定性问题的另一种方法。它通过一对对偶函数（信任函数和似然函数）定量表示信息的不确定性。粗糙集理论和证据理论这两种工具相似却又不同，众多学者对它们之间的关系进一步展开了研究。Yao等人[20]给出了用信任函数和似然函数来刻画经典粗糙集中上下近似的可能性；Wu等人[21]从证据理论角度出发研究了Pawlak的粗糙约简。上述研究均是刻画经典Pawlak粗糙集同证据理论的联系，但没提及功能更强大的直觉模糊粗糙集与证据理论之间的关系以及通过两者结合进行知识约简，且国内外对此方向的研究较少。

2 基本知识

首先介绍直觉模糊粗糙集和证据理论的基本知识。

2.1 直觉模糊粗糙集

定义1（直觉模糊粗糙集[15]）设U为非空集合函数μ:U→[0,1]，ν:U→[0,1]，且 ∀x∈U，满足 0≤μ(x)+ν(x)≤1，则称集合A={＜x,μ(x),ν(x)＞|x∈U}为直觉模糊集。μ(x)、ν(x)分别表示U中元素属于A的隶属度和非隶属度，πA(x)=1-μ(x)-ν(x)表示对元素x属于A的怀疑度；s(A(x))=μ(x)-ν(x)为集合A关于x的得分函数；h(A(x))=μ(x)+ν(x)为集合A关于x的精确函数。

从上述定义可知，传统集合是直觉模糊的特例。用直觉模糊集合形式表示，即对A∈P(U)，如果x∈A，则A(x)=(1,0)；如果x∉A,则A(x)=(0,1)。

定义2（直觉模糊粗糙集运算[15]）有模糊集A={＜x,μA(x),νA(x)＞|x∈U}和B={＜x,μB(x),νB(x)＞|x∈U}则可得如下运算：

（1）s(A(x))＜s(B(x))⇒A(x)≺B(x)

（2）s(A(x))=s(B(x))∧h(A(x))=h(B(x))⇒A(x)=B(x)

（3）s(A(x))=s(B(x))∧h(A(x))＜h(B(x))⇒A(x)≺B(x)

（4）s(A(x))=s(B(x))∧h(A(x))＞h(B(x))⇒A(x)≻B(x)

由定义可知，若A(x)=(0.2,0.5)，B(x)=(0.3,0.6)，则s(A(x))=s(B(x))=-0.3,h(A(x))=0.7,h(B(x))=0.9，故A(x)≺B(x)。

性质1对模糊集A={＜x,μA(x),νA(x)＞|x∈U}和B={＜x,μB(x),νB(x)＞|x∈U}而言，具有以下性质：

（1）A⊆B⇔μA≤μB,νA≥νB

（2）A⋂B⇔{＜x,min(μA,μB),max(νA,νB)＞|x∈U}

（3）A⋃B⇔{＜x,max(μA,μB),min(νA,νB)＞|x∈U}

（4）A⊕B={＜x,μA+μB-μA∗μB,νA(x)∗νB(x)＞|x∈U}

（5）A⊗B={＜x,μA∗μB,νA(x)+νB(x)-νA(x)∗νB(x)＞|x∈U}

（6）λA={＜x,1-(1-μA)λ,(ν(x))λ＞|x∈U}

（7）Aλ={＜x,(μ(x))λ,1-(1-ν(x)λ)＞}

（8）～A={＜x,νA(x),μA(x)＞ |x∈U}

由性质1可得如下定义。

定义3（模糊集和运算、积运算[9]）模糊集簇Ai={＜x,μAi(x),νAi(x)|x∈U＞}，且i=1,2,…,n，则关于和⊕运算算子和积⊗运算算子的定义如下：

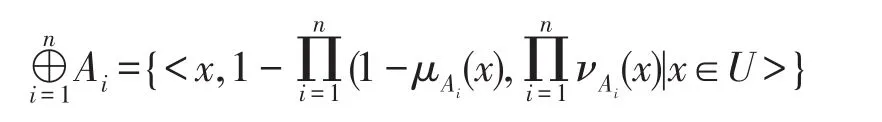
定义4（普通优势关系[9]）直觉模糊信息系统IFIS=(U,AT=C,V,f)且U为非空论域，C为条件属性集，函数f为值域函数，f(x,c)=(μc(x),νc(x)),c∈C可得关系，则称为普通优势关系。

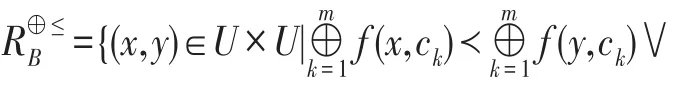
定义6（广义和优势的上、下近似关系[10]）IFIS=(U,AT=C,V,f)为直觉模糊信息系统，对∀X⊆U有：

根据广义和优势关系的上近似和下近似的定义可知其具有如下性质。

性质2IFIS=(U,AT=C,V,f)为直觉模糊信息系统，C={c1,c2,…,cm}，∀X,Y⊆U有：

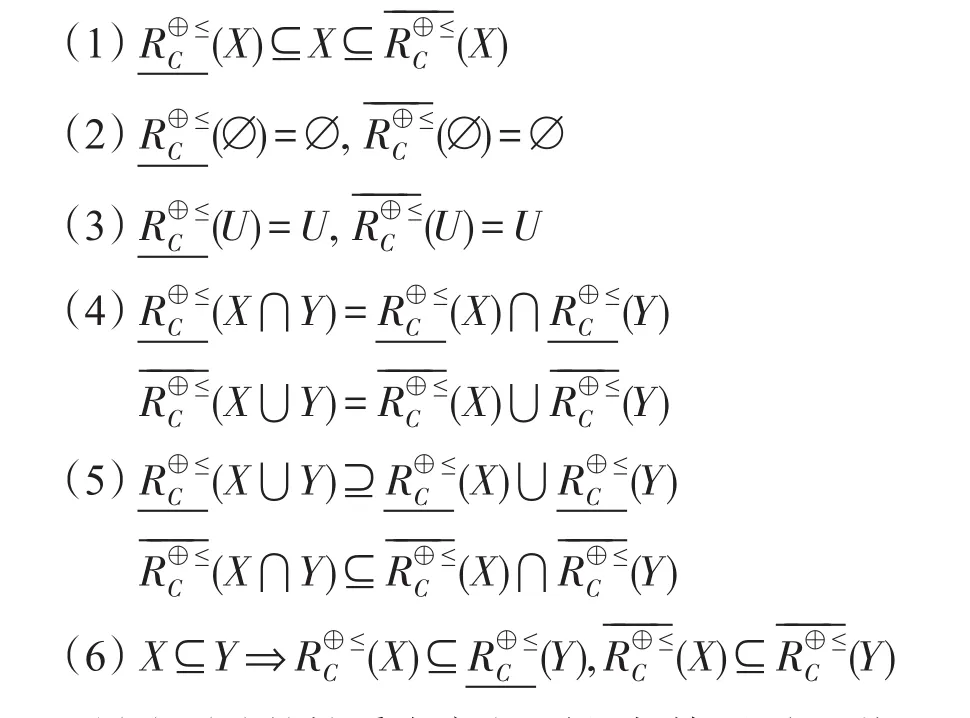
因（1）～（6）的性质由定义5得到，故不再证明。

2.2 证据理论

定义7（mass函数[19]）设Θ为识别框架，A是Θ中的任意子集，定义在识别框架Θ的函数m:2Θ→[0,1]满足如下条件：

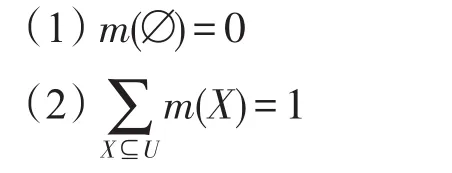
则称函数m为2Θ上的基本可信度分配函数或mass函数。

m(A)表示证据对A的信任度。若m(A)＞0，则A为焦元，所有焦元的并称为核，记作F。同时根据基本可信度分配函数可得出信任函数和似然函数的定义。

定义8（信任函数、似然函数[19]）设Θ为识别框架，A是Θ的任意子集，m是识别框架Θ上的基本可信度分配函数。

则称Bel(X)和Pl(X)分别为信任函数和似然函数。

信任函数Bel(X)表示对X为真的信任度，似然函数Pl(X)表示不怀疑X为真的信任度，且Bel(X)=1-Pl(～X)。同样也可以根据半加性定义信任函数。

定义9（信度函数[19]）对识别框架Θ的任意子集2Θ，若函数Bel:2Θ→[0,1]满足如下条件：

则称函数Bel:2Θ→[0,1]为信度函数。

3 直觉模糊粗糙集与证据理论的关系

文献[20]研究表明Pawlak粗糙集和基于覆盖的粗糙集所获得的下、上近似均可通过证据理论的信任函数和似然函数分别刻画。接下来，将分析直觉模糊粗糙集和证据理论之间的关系，是否也能满足以上特征。

定理1IFIS=(U,AT=C,V,f)为直觉模糊信息系统，A⊆AT=C,∀X⊆U，则：

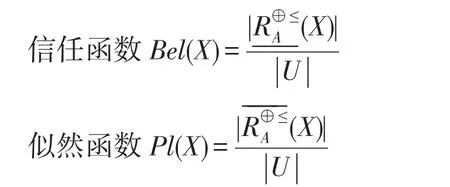
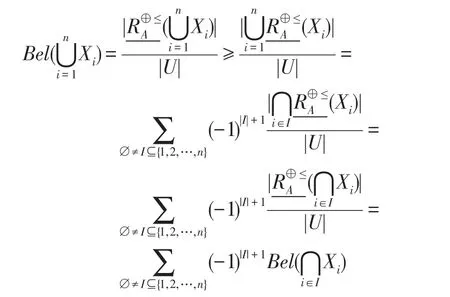
通过对上述定理分析得出，直觉模糊粗糙集的下、上近似也可以用证据理论的信任函数和似然函数分别刻画。接下来，给出此时的mass函数表达式。

如果不满足上面的条件，m(X)=0。

证明由定理1可得如下结果：

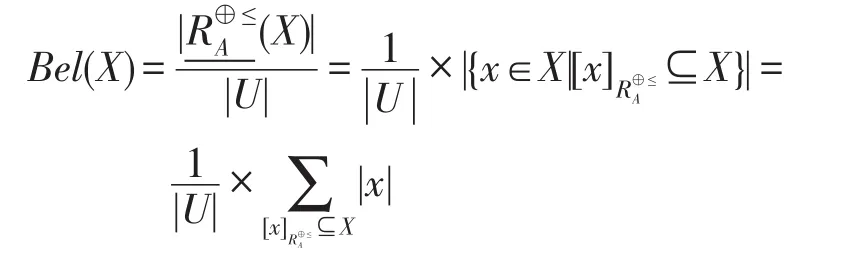
下面给出实例说明直觉模糊粗糙集和证据理论相结合的属性约简方法。

例1现有一组数据如表1，用于判断硬盘是否为损坏。其中论域U={x1,x2,x3,x4,x5,x6,x7,x8,x9,x10}，条件属性为C={c1,c2,c3,c4,c5}。

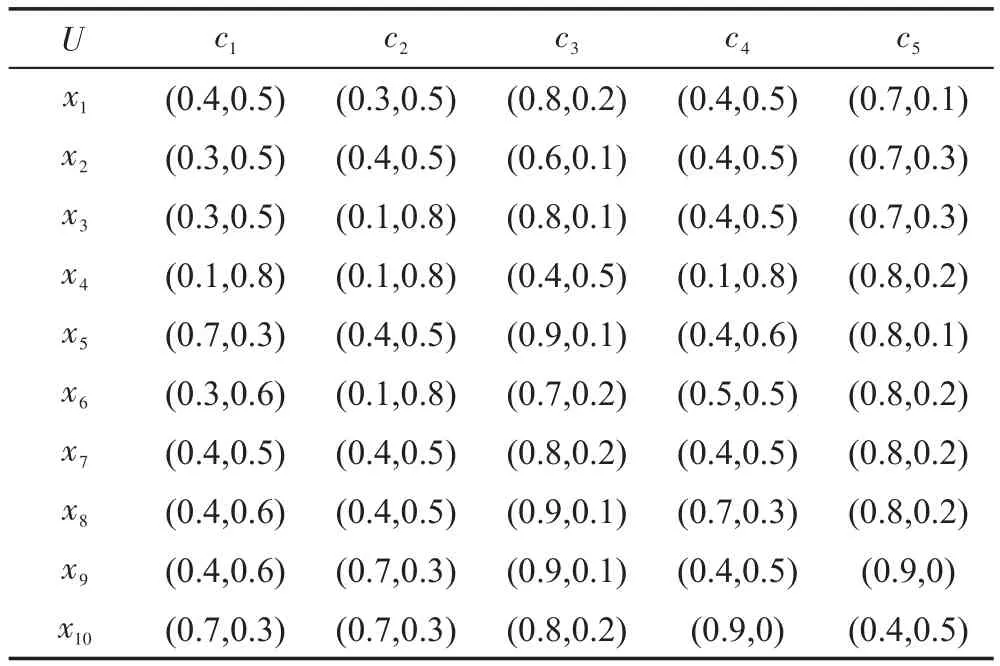
Table 1 Intuitive fuzzy information systems表1 直觉模糊信息系统

由定义3计算可得如下结果：

同理可得：

由定义1可得各元素的得分：

故可得如下排序结果：

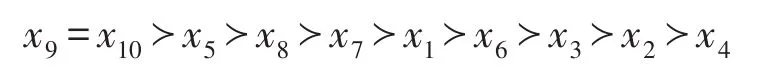
对应的广义和优势关系的等价类为：

令X={x8,x9,x10}，则对应的上、下近似为：

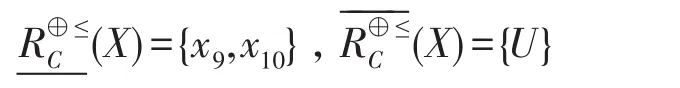
对应的质量函数为：

4 决策系统的约简

决策系统可分为协调决策表和不协调决策表两种。进行属性约简前，先给出协调决策表和不协调决策表的定义。

定义10（直觉模糊不协调决策系统[20]）IFDS=(U,AT=C⋃{d},V,f)为直觉模糊决策系统，分别为基于条件属性集C和决策属性集d计算而得到的广义和优势关系{Cl1,Cl2,…,Cln}。若∀x∈U有，则IFDS=(U,AT=C⋃{d},V,f)为协调决策系统；若∃x∈U有，则称IFDS=(U,AT=C⋃{d},V,f)为不协调决策系统。

定义11（直觉模糊决策系统的三种约简[20]）IFDS=(U,AT=C⋃{d},V,f)为直觉模糊决策系统，属性子集A⊆C，则：

（2）若∀Clt,1≤t≤n，BelA(Clt)=BelAT(Clt)，则称A是相对信任协调集。若A为相对信任协调集且A的任意非空真子集B不为相对信任协调集，则称A是相对信任约简。

（3）若∀Clt,1≤t≤n，PlA(Clt)=PlAT(Clt)则称A是相对似然协调集。若A为相对似然协调集且A的任意非空真子集B不为相对似然协调集，则称A是相对似然约简。

定义11从分类、信任度和似然度三个角度给出了相对约简的概念。接下来，协调决策系统中分析三者的一致性。

定理4IFDS=(U,AT=C⋃{d},V,f)为协调直觉模糊决策系统，属性子集A⊆C，则有：

（1）A为相对协调集、相对信任协调集和相对似然协调集三者等价。

（2）A为相对约简、相对信任约简和相对似然约简三者等价。

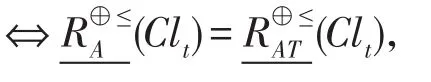
（2）同（1）可证。

由定理4可知在协调直觉模糊决策系统中，相对约简、相对信任约简和相对似然约简等价，要获得三者，只需确定其中之一即可。接下来，将研究不协调直觉模糊决策系统的约简关系。针对不协调决策系统，其处理方式是将它转化为协调决策系统。同理,给出由不协调直觉模糊决策系统得到广义直觉模糊决策系统的定义12。

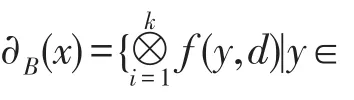
定义13（广义直觉模糊系统的三种约简[20]）IFDS=(U,AT=C⋃{∂C},V,f)为广义直觉模糊决策系统，属性子集A⊆C，则：

以下将给出一个算例表明如何将不协调决策系统转化为协调决策系统。

例2给定决策表2，用于判断硬盘是否损坏。其中论域U={x1,x2,x3,x4,x5,x6,x7,x8,x9,x10}，条件属性为C={c1,c2,c3,c4,c5}，决策属性d表示接受硬盘的与否概率。

Table 2 Intuitionistic fuzzy decision making system表2 直觉模糊决策系统

由定义1的得分函数和精确函数可计算属性论域的覆盖如表3。

Table 3 Dominant class of decision attributes表3 决策属性的优势类

根据定义5可得广义优势关系对论域的覆盖如表4。

Table 4 Dominant class of condition attributes表4 条件属性的优势类

根据定义10可知，决策表3为不协调决策系统，故可根据定义11来计算转换后的决策值。

同理可得：

直觉模糊广义决策系统如表5所示。

Table 5 Intuitionistic fuzzy generalized decision system表5 直觉模糊广义决策系统

接下来，分析广义相对约简和相对约简之间的关系。

定理5IFDS=(U,AT=C⋃{∂C},V,f)为广义直觉模糊决策系统，属性子集A⊆C，则：

（1）A为广义相对协调集当且仅当A为相对协调集。

（2）A为广义相对约简当且仅当A为相对协调集。

证明（1）由定义可知，若，故A是相对协调集；同理可得，若A是相对协调集，则A是广义相对协调集，故结论成立。

定理6IFDS=(U,AT=C⋃{d},V,f)为广义直觉模糊决策系统，属性子集A⊆C，则：

（1）A为广义相对协调集、广义相对信任协调集和广义相对似然协调集三者等价。

（2）A为广义相对约简、广义相对信任约简和广义相对似然约简三者等价。

证明同定理4，故不再赘述。

5 结束语

协调决策系统和不协调决策系统的约简通常不一致。本文首先分析了直觉模糊粗糙集与证据理论之间的关系，即当上、下近似具有可加性和可乘性时，直觉模糊粗糙集所获得下、上近似可通过证据理论的信任函数和似然函数分别刻画。接下来，分析了决策系统约简的一致性，当为协调决策系统时，直觉模糊决策系统的相对约简、相对信任约简和相对似然约简三者等价；当为不协调决策系统时，在广义决策优势关系下，协调决策系统的约简与不协调决策系统的约简一致。通过上述研究，进一步完善了直觉模糊粗糙集决策约简理论。