融合网络结构和节点属性的链接预测方法*

张 昱，高克宁，陈 默，于 戈

东北大学 计算机科学与工程学院，沈阳 110819

1 引言

近年来，链接预测作为社会网络研究的一个基本问题一直都是网络研究的重点。早期的链接预测研究方法集中于利用网络结构信息计算出网络中两个节点间的相似性[1-3]，以相似性的度量值来确定节点间能否产生链接的概率，从而达到预测的目的。共同邻居数（common neighbors，CN）即是其中一种典型方法，即通过两个节点所拥有的共同邻居数量来预测两者建立链接的可能性，共同邻居越多，两者建立联系的可能性就越大。共同邻居数具有计算简单且效果好的优点，一直是链接预测方法的基准指标。此外，还有很多类似的根据网络结构计算节点相似性的方法，如Adamic-Adar（AA）[4]、Katz[5]等。

社会学的研究表明，网络中的两个节点既可能因为在网络结构上相近而产生联系，也可能因为两者属性相似而产生联系。随着信息社会网络的发展，越来越多的网络数据包含了大量的节点属性信息，这给社会网络链接预测的研究带来了很大的机遇和挑战。传统的基于网络结构的方法大都忽略或弱化了节点的属性信息，而近年来不少研究都表明这些属性信息对于网络的链接预测效果有明显提升[6-10]。但如何将网络结构信息和节点属性信息有效地结合起来用于链接预测一直是一个研究的难题。

传统的计算节点相似性方法中，RWR（random walk with restart）方法[11]具有较好的预测效果。RWR方法本质上是PageRank算法的变形，其假设在一个具有N个节点的网络中，一个随机游走粒子从节点i出发，并在每走一步时都以一定的概率返回初始位置，其更新规则如下：

其中，向量πi是一个N×1的向量，每一个元素πi,j都表示节点i到j的可能性度量值；P是概率转移矩阵，P的元素Pij表示节点i到j的转移概率，这里实际上就是经过归一化的网络权值矩阵；ei也是N×1的向量，表示初始态，只有第i个元素为1，其他元素为0；d是一个常数，它的取值实际上是收敛性和有效性的一个折中，d越小收敛速度越快，但收敛值的意义也越小。最终πi的收敛值即是节点i到其他节点的相似性度量值，也就是它们是否形成链接的概率值。

RWR方法相对于其他相似性度量方法有一个天然的优势，即转移概率矩阵P实际上是由网络的边权生成的。如果仅仅知道网络结构，那边权只能平均分配，即每一个节点游走到它的任意一个邻居节点的概率是相等的。如果网络数据中还包含节点的属性信息，那就可以将两个相邻节点的属性映射成两个节点连边的边权重，这样就保证了游走粒子更倾向于游走到与当前节点属性上更相似的邻居节点上。如此，网络结构信息和节点属性信息就在RWR方法的框架下自然地统一在一起用于链接预测。文献[7]采用此方法并通过优化算法学习出网络边权重，取得了较好的效果。但是，此类传统的RWR方法有一个固有的缺陷，就是随机游走被限制在网络拓扑结构上。例如，两个在网络中不连通的节点，其节点属性相似度很高，在实际上是有可能组成新的连边，但应用传统RWR的方法则无法预测出来。

本文针对此问题设计了一种将网络结构信息和节点属性信息统一在一个层次的框架内的方法，并给出了针对大规模网络的近似计算算法，通过在网络公开数据集上进行的实验表明该方法相对于其他链接预测方法有较为明显的效果提升。

2 方法

2.1 方法概述

社会网络图可由G=(V,E)表示，其中V和E分别为网络的节点集合和边集合。对于每个节点i∈V，都带有一个属性向量，表示为xi。本文的目标就是利用这些输入设计一个新的基于RWR方法的链接预测框架。

本文方法结合了两种链接预测的基本假设：（1）两个节点在网络拓扑中的联系越“近”，两者越有可能产生链接；（2）两个节点的属性越相似，两者越有可能产生链接。本文提出的方法是基于属性相似性的随机游走方法，简称为“ARWR（attributed random walk with restart）”。基于假设（2），如果两个节点的属性相似，即使它们在网络上的“距离”远，也可能产生链接。因此，ARWR方法将网络虚拟成为一个全联通图H，这样对于随机游走粒子而言，它在每一步游走过程中，都有机会走向任意一个节点，而不是像传统的RWR方法只能走向网络上与其相邻的节点。文献[12]提出了将节点属性也当成网络中的节点，从而将节点属性融合到网络中再采用随机游走的方式进行链接预测。文献[13]则提出了类似的计算含属性网络的PageRank值方法，将网络分解成原始社会网络无权图G和带有属性权重的全联通网络H，并使随机游走粒子同时在两个网络中游走。本文与上述文献不同之处是在不增加网络节点数量的条件下融合了节点属性信息，并且随机游走粒子按照传统RWR方法每走一步都可能以一定的概率返回出发点，最终给出了面向链接预测问题的实验结果。

为了简化问题，可以将ARWR方法理解为随机游走粒子在每一步行动中，既有机会按照传统的RWR形式在原始只有网络拓扑结构信息的网络G中移动，也有可能在只包括属性相似度信息的全联通的网络H中移动。G的转移概率矩阵P维持不变，而H的转移概率矩阵Q则是通过节点间的属性相似度生成的权值矩阵。因此ARWR的更新规则可调整为：

其中，α和β分别表示粒子在G和H中游走的可能性。P为网络图G的转移概率矩阵，按传统的定义，每一个粒子都有均等的机会移动到它的邻居节点。

Q是全连通网络H的转移概率矩阵，其元素Qij应体现节点i和j的属性相似程度，因此定义如下：

其中，sij表示节点i和j的属性相似度，对其进行标准化处理，使得每个节点上的粒子向其他节点游走的概率总和为1。如果已知两个节点i和j的属性向量，则衡量它们的属性相似度有多种方法，本文采用了皮尔逊相关系数，sij的范围从-1到+1，数值越大说明i和j的相似性越高，本文采用了一个映射函数f(x)=(x+1)/2将该系数的范围映射至[0,1]。本文还尝试了其他若干种标准的相似性度量方法，如欧氏距离、余弦相似度等，结果发现对最终的链接预测效果影响非常小。因此，本文仅采用皮尔逊相关系数报告最终的结果。

2.2 模型简化与计算

首先，α和β的选择对预测结果至关重要，它们分别表示游走粒子在G和H上游走的概率，同时也表示着网络结构和节点属性这两类不同的信息对链接形成的贡献程度。然而，各种实际的社会网络千差万别，并且实际采集到的数据也不同，因此很难确定究竟是网络结构还是节点属性对链接预测的结果影响更大，也很难度量它们各自的影响程度。因此，也就很难确定出α和β的比例。此外，游走粒子在每一步返回初始节点的概率θ=1-α-β同样需要 确定。

为简化模型，首先选择固定的返回概率θ。在PageRank和RWR的很多经典文献中都给出θ=0.15[11,14]的取值，它代表着RWR方法在收敛速度和收敛结果有效性上的折中，本文的实验也采用这个取值计算并给出结果。一旦θ确定，因为α+β=1-θ，所以可表示β=1-θ-α。

为实现快速的计算，本文对式（2）进行进一步的简化。首先定义一个N维向量r，其元素ri定义为：

证明如下。对于每一个节点i：

如前所述，α和β的比例无法确定，因此将其当成随机变量来处理并建立它们的概率分布模型。最终ARWR将计算基于α和β的分布的π的期望E(π)作为节点间的链接可能性度量结果。对上式整理后得到其稳态解为：

使用矩阵的Neumann级数展开，得到：

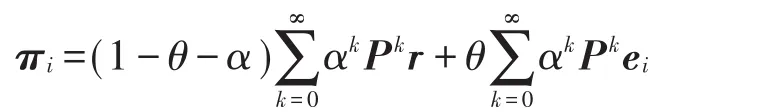
于是得到πi的期望，写成：

由上式可看出，为计算这个E(πi)，需要计算两个分量各自从0到∞的和。于是可做如下处理：

因为P、r、ei都是非负的量，而α则是(0,1-θ)之间的一个随机量，这就保证了上式的所有分项都是非负的，所以可通过循环累加的方式计算E(πi)的近似值，即：

接下来就是为α选择一个合适的概率分布模型，但关于此参数并没有任何先验知识，因此本文在实验中首先假设α为一固定值，然后分别测试不同的α取值并根据测试结果选择合适的概率分布，概率分布确定后即可计算E(αk)的值代入获得E(πi)的结果。本文将在实验环节对α取值做进一步分析。

至此，本文方法叙述完毕，下面用一个完整的伪代码算法描述将上述方法整合在一起。

算法1ARWR计算算法

输入：图G=(V,E)，其中每一个节点i∈V都有一个属性向量xi，随机游走粒子的返回概率θ、α具有确定的概率分布，以及收敛容差ε。

输出：每一个节点i游走到网络中其他节点的概率πi。

1.标准化所有的属性向量xi；

2.利用式（5）生成r；

3.利用式（3）生成P；

4.ρA=(1-θ-E(α))r

5.ρB=θei

6.π=ρA+ρB

7.k=1

8.whileρ＞εdo

11.π=π+ρA+ρB

12.k=k+1

13.end while

由算法的伪代码可知，P和r均为一次性计算，在P和r固定的情况下，算法中的每一次迭代中主要的计算消耗为PρA，其计算的时间复杂度为O(N)。因此，使用ARWR算法计算出网络中所有节点对相似性的时间取决于网络规模（N）和针对每一个节点进行计算的迭代次数，这与传统的RWR方法的时间复杂度是一致的[15]，这表明了ARWR算法与原始的RWR算法相比并不会降低运算速度。

3 实验

3.1 实验数据集

为了测试本文方法的适应性和有效性，选取了两种不同类型的数据集。数据集均从斯坦福大学的网络数据网站（http://snap.stanford.edu/data/）下载，是在社会网络研究中使用广泛的公开数据集。

数据集1（CA-HepPh）此数据集为一个论文合作网络，涵盖了1993年1月至2003年4月间高能物理某领域的论文数据。数据集中，每个节点表示一个论文作者，如果作者i和作者j至少有1篇共同署名的论文，则i和j之间产生一条无向边。

数据集2（soc-Pokec）Pokec是斯洛伐克的一个非常流行的在线社交网络。此数据集包含该网络的带方向的好友关系以及用户的多种属性信息，如性别、年龄、爱好等。

数据集1是具有社会网络性质的合作网络，仅包含网络结构数据且网络边是无方向的。数据集2是标准的在线社会网络，连边是有方向的，并且其除了好友关系之外还包括节点的多种属性数据。这两个数据集涵盖了各种不同的情况，具有广泛的代表性。表1总结了两个数据集的典型网络特征。

Table1 Network characteristics of datasets表1 实验数据集的网络特征

3.2 数据整理

数据集1是无向图，为了使用本文算法，将其看成是有向图，即将每一条无向边转换为两条方向相对的有向边。在数据集1中，只有网络结构信息，即节点间的好友关系，并不包括节点的属性信息。但在实际应用中，可以从网络结构信息中提取出节点的属性信息，这部分基于结构的属性信息实际上对链接预测有很大帮助。因为最终基于RWR方法的随机游走虽然是基于网络结构的方法，但是其遵循的是一阶马尔可夫模型，而网络结构中的更高阶的信息被掩盖了。因此，将更多的这类网络结构信息转换成节点的属性信息即可更好地服务于链接预测模型。

使用网络拓扑结构信息提取属性相似度不能按照计算两者属性向量相似度的方式进行。例如，两个节点的度数都很大并不能说明两者可能产生链接。因此本文针对数据集1选取了能够表示出节点间结构相似性的若干个度量指标用于计算sij，包括：（1）共同好友数；（2）2-hop共同好友数；（3）3-hop共同好友数。为避免上述的属性值过大，计算时均进行了归一化处理，之后再对各指标进行加和形成节点的相似性取值sij。

数据集2本身包含节点的自然属性信息，为验证属性信息对链接形成的影响，本文选取了其中5种有代表性的可用于度量节点相似性的属性：（1）年龄；（2）所在地区；（3）工作领域；（4）所讲语言；（5）爱好。

由于数据集2的数据量过大且属性信息不全，本文从该数据集中选取了属性信息完整并度数大于10的节点形成了一个子集用于实验。上述属性中只有年龄为数值型数据，做归一化处理即可；其他属性为非数值型离散数据，在计算属性向量相似度时，先对其进行one-hot code方式的编码，再采用皮尔逊相关系数计算节点间的属性相似度。

3.3 比较和评价方法

本文使用如下4种链接预测指标与本文提出的方法进行比较。

（1）共同邻居数（CN），此指标为链接预测领域的基准指标。

（2）AA，该指标最早提出时用作度量两个网页间的相似性[4]，表示为：

此处N表示节点的好友集合，这个指标的基本思想是两个节点的共同好友对于两节点建立链接的支持程度不同，其中度数较大的好友对建立链接的支持度被削弱。

（3）RWR，如前所述，该指标仅基于网络拓扑结构进行随机游走。

（4）RWRW（RWR on weighted network），这是将属性相似性信息与网络结构信息相结合的最基本的方法，使用节点间属性相似度作为其边权值，随机游走则按照边权形成的概率进行。

链接预测的评价采用的是标准AUC（area under curve）值，简述如下：将网络数据集分成训练集和验证集，首先随机取出网络中10%的链接作为有链接的验证集，余下的含有原始网络90%链接的网络作为训练集，此外从无链接节点对中随机取出与有链接验证集等量的节点对作为无链接验证集。分别计算两个验证集中的各节点对在训练集网络上的各个度量指标（5种），得出各类度量值的AUC值以比较预测结果。AUC值的计算方法如下：

从链接集合与非链接集合中随机取出链接进行测试，比较其在训练数据集上各度量指标的值，实验共重复n次，n′表示链接集的分值高于非链接集分值的次数，n″表示两者相等的次数，最终得到AUC分值作为此类链接预测方法的评估值。

3.4 实验结果与分析

本文方法将参数α当作随机变量来处理，在没有任何先验知识的情况下，最合理的假设是α服从[0,θ]间的均匀分布。但为了分析不同数据集下采用不同α的实际效果，实验中除了设α服从[0,0.85]间的均匀分布外，还对α取[0,θ]间的多个固定取值，步长为0.1，针对两种不同的数据集，得到AUC预测结果，如图1所示。

Fig.1 Performance of link prediction with different parametersα图1 参数α在不同取值下的链接预测效果

首先，由图1可知，不同数据集下α的最优取值并不相同，这也说明了在不同的网络中，链接形成的机制十分复杂，不是由网络结构或是节点属性独立决定的；其次，将α看成服从均匀分布并不能保证得到最优的结果，α在不同类型网络下的分布还有待进一步大量的实验分析；最后，从本文的两种实验数据集的结果观察可知，α偏大更有可能取得较好的预测效果，说明网络结构信息对链接预测的影响还是非常大。但当α达到最大时（如图中α=0.8），预测的效果有一定程度的降低，说明节点属性信息对提高预测效果是有帮助的。

实验选取了图1中的最优AUC值作为本文方法的最终预测结果，与其他4种预测指标进行比较，结果如表2所示。

Table 2 AUC comparison of different methods表2 不同方法的AUC比较

这个结果表明本文方法可以有效地利用节点的属性信息提高链接预测的效果。

4 结束语

社会网络中大量的节点属性信息可以与网络结构信息相结合用于网络的链接预测已经成为研究者的共识，本文基于此构建了一种基于随机游走的方法进行链接预测，并将节点的属性相似度信息融合进网络中参与随机游走过程，并给出了一种可适用于大规模网络计算的近似算法。最后在不同的数据集上进行了方法的验证，实验表明此方法可有效地提高链接预测的效果。

未来尚有两个问题需要进一步研究和实验：一是如何针对不同类型的网络，快速地找到参数α的最优值，从而提高链接预测的精确度；二是借鉴其他的研究成果[16-17]，采用更有效的机器学习模型得到节点间的属性相似度，从而建立更为精确的转移概率矩阵。