粗糙集的Mallow’s Cp选择算法*

杨贵军，于 洋

天津财经大学 统计学院，天津 300222

1 引言

由Pawlak提出的粗糙集是一种有效的机器学习特征提取方法[1]，能从数据中归纳出易于理解的分类规则以揭示数据背后蕴藏的信息特征，不受限于数据分布，在经济[2-4]、文本挖掘[5-6]等多个领域有广泛应用。不同粗糙集构造方法得到的粗糙规则一般不同，在实际应用中，为了较好反映数据的真实关系，选择优良粗糙集至关重要。

通常，择优粗糙集的标准是其在新样本上的泛化误差。泛化误差小的粗糙集为优良粗糙集，在新样本上具有强泛化能力。然而新样本事先并不可知，无法计算泛化误差，许多文献以测试集上的误判率或正确率作为泛化能力替代来评估粗糙集[7]。如Jaworski基于粗糙集分类规则的正确率与覆盖率构建了粗糙集的新评估指标[8]。Cornelis等比较了多种基于模糊容差关系的粗糙集属性约简方法，并给出了具有高正确率的实证结果[9]。张维等组合集成学习与半监督学习给出了新粗糙集属性约简方法，用正确率评估了新方法的效果[10]。刘偲等结合测试代价提出测试代价敏感的决策粗糙集正域约简算法，并以分类正确率评估新算法的分类效果[11]。徐健锋等提出基于混淆矩阵的多目标优化三支决策模型，新方法的准确率更高[12]。

综上所述，目前研究者大多以误判率为粗糙集择优标准。然而，误判率虽然计算简单直观，但其仅关注粗糙集在测试集中的分类准确性，未考虑粗糙集的复杂度[13-14]。且误判率并非总能真实反映出粗糙集的泛化能力，粗糙集在测试集中误判率最低，在新样本上的泛化能力并不总是最强。如本文第4章显示，对于Breastcancer数据集，分别采用基于最大概率的粗糙集方法和基于贝叶斯的粗糙集方法构造500对粗糙集，其中在测试集中最低误判率的500个粗糙集，只有362个粗糙集在新样本上泛化能力最强。特别是当测试集中多个粗糙集之间的误判率相差小时，采用误判率标准不易选出在新样本上泛化能力最强的粗糙集。

Mallow’s Cp准则最早用于模型中的变量选择。研究者如Hansen、张新雨等进一步将其思想推广应用到模型选择与模型平均等问题[15-16]。Mallow’s Cp准则兼顾了模型的数据拟合度与模型复杂程度，能有效减小过拟合风险。针对决策属性为两分类的数据集，本文引入粗糙集的Mallow’s Cp选择算法。利用Logistic模型表示非线性粗糙集分类规则，Logistic模型的Cp值即为对应粗糙集的Cp值，以Cp值为粗糙集的择优标准。Mallow’s Cp准则在多个粗糙集的择优时兼顾粗糙规则的分类准确性与复杂度，常选择出强泛化能力的粗糙集。实验结果显示，当多个粗糙集在测试集中误判率差异小时，新算法常常选出强泛化能力的粗糙集。

2 预备知识

2.1 Pawlak粗糙集

定义1[17（]信息系统）假设S=(U,A,V,f)为一个信息系统，其中U={u1,u2,…,un}为样本的非空有限集合，即论域；X={x1,x2,…,xk}为k维条件属性，Y 为决策属性，A=X⋃Y为属性全体(X⋂Y=∅)；属性值的集合记为；f:U×A→V是信息函数，为每个样本的每个属性赋予一个信息值，即：∀a∈A,u∈U,f(u,a)∈Va。

定义2[18（]粗糙集）定义R为U上的等价关系，以U R={[u]R|u∈U}表示R的所有等价类构成的集合，其中[u]R表示样本u关于R的等价类，则∀B⊆U,B的上下近似集定义为：

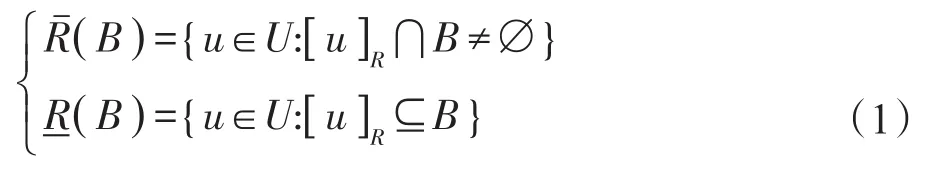
2.2 粗糙集构造方法

采用不同粗糙集构造方法，得到不同的粗糙集，分析结果往往有差异。择优准则是为了选择出在新样本上强泛化能力的粗糙集。目前，粗糙集构造方法主要有基于最大概率的粗糙集方法和基于贝叶斯的粗糙集方法[19]。本文研究二分类问题，决策属性Y取值为0或1。为简化叙述，记一类取值为c，则另一类取值为1-c(c=0,1。)

方法1[19（]基于最大概率的粗糙集方法）该方法通过比较第i(i=1,2,…,n)个样本ui的条件属性Xi={xi1,xi2,…,xik}在第c类和第1-c类上的概率大小来判断分类，第c(c=0,1)类上的概率公式为：

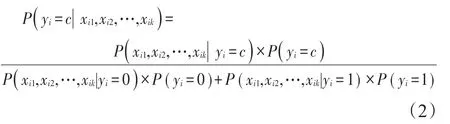
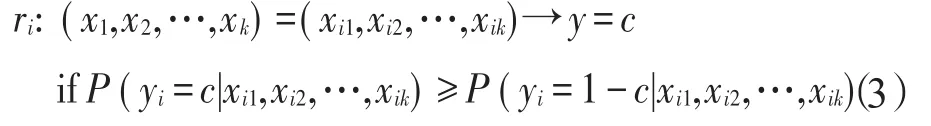
方法2[19（]基于贝叶斯的粗糙集方法）该方法通过比较本属于1-c(或c)类的第i(i=1,2,…,n)个样本ui的条件属性 Xi={xi1,xi2,…,xik},被判为c(或1-c)类的误判平均损失大小来判断分类。将条件属性为xi1,xi2,…,xik时属于1-c(c=0,1)类的第 i(i=1,2,…,n)个样本ui判为c类的误判损失记为λ(yi=c|xi1,xi2,…,xik)≥0，则将ui误判为c类的误判平均损失为：

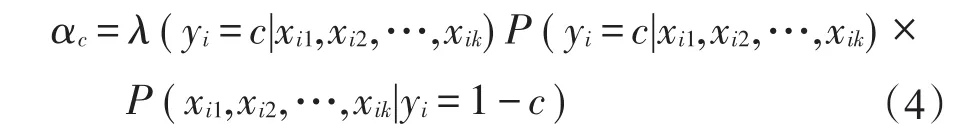
若αc≤α1-c，则将样本ui判为第c类，分类规则为：

两种方法构造的粗糙集分类规则并不总是一致，两者的误判率也往往不一样。

2.3 基于误判率的粗糙集择优

记两种方法得到的粗糙集分别为B1和B2，则对应的误判率为粗糙集Bh分类错误的样本数占样本总数的比例，记为E(Bh;U)(h=1,2)[7]。误判率准则选择的较优粗糙集Bh满足：

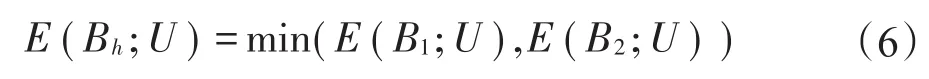
误判率关注粗糙集的分类准确性，利用粗糙集分类误判率反映粗糙集的优良性，仅考虑粗糙集的分类结果，未考虑粗糙集的复杂程度，容易出现过拟合问题，导致在测试集上误判率低的粗糙集不一定具有强泛化能力。

3 粗糙集的Mallow’s Cp择优

上述提到误判率择优粗糙集时可能出现过拟合问题，从而选择的粗糙集并非总是具有强泛化能力，针对该问题，本文引入同时考虑分类精度与粗糙集复杂度的Mallow’s Cp准则，以期减少过拟合情况，择优出强泛化能力的粗糙集。为将Mallow’s Cp准则用于粗糙集择优，需要利用Logistic模型将非线性的粗糙集分类规则表达为线性形式。此时，基于粗糙集分类规则，Logistic模型与粗糙集一一对应。计算Logistic模型的Cp值，最小Cp值的Logistic模型最优，其对应的粗糙集为所选择的最优粗糙集。其中，Logistic模型的因变量为决策属性yi，解释变量由粗糙集的分类规则定义，为避免共线性问题，仅选取判为c类的分类规则，记为第一类。

定义3（解释变量）设由数据得到的第一类粗糙集分类规则共有m个，为：则相应Logistic模型的解释变量定义为：

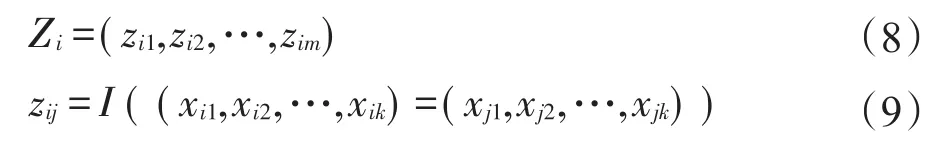
其中，zij为由第j个分类规则所定义的解释变量，是判断第i个观测是否符合分类规则rj的条件(x1,x2,…,xk)=(xj1,xj2,…,xjk)的示性函数，i=1,2,…,n(n为观测个数)，j=1,2,…,m(m为新变量个数)。

定义 4（Logistic模型） 以Zi=(zi1,zi2,…,zim)为解释变量，yi为因变量构建的Logistic模型定义为：

Logistic模型与粗糙集存在一一对应关系，本文认为最优Logistic模型对应的粗糙集为最优粗糙集。

定义5（Cp值）记两种不同的粗糙集分别为B1和B2，第一类粗糙集分类规则个数分别为m1和m2个，对应Logistic模型的残差平方和分别为sse1和sse2，则Cp值定义为：

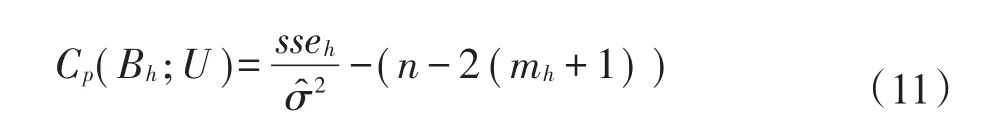
其中，以两种粗糙集构造方法得到的第一类粗糙集分类规则组成规则全集，并剔除重复规则，设共有m1+m2-p个（p为m1和m2个规则中重复的规则个数），为对应Logistic模型的方差σ2的最大似然估计，h=1,2。

这里，Mallow’s Cp准则将两种粗糙集构造方法得到的第一类粗糙集分类规则看作是两个规则子集，将两个规则子集汇总并剔除重复规则后的规则视为规则全集，选择的是在同一规则全集下兼顾精度与复杂程度的最优规则子集。Cp值分为两部分，第一部分依据规则子集与规则全集的相对解释程度考察粗糙集的准确度，第二部分依据规则子集个数的函数考察粗糙集的复杂程度。当两个规则子集的准确度相差较大时，第一部分起决定作用。准确度高的规则子集对应第一部分值较小，对应Cp值较小。当两个规则子集的准确度相近时第一部分值相差较小，此时选择结果主要取决于第二部分。规则个数较少的子集复杂度较低，对应第二部分函数值较大，对应Cp值较小。Mallow’s Cp准则兼顾粗糙集的准确度与复杂程度。满足Cp(Bh;U)=min(Cp(B1;U),Cp(B2;U))的Logistic模型更优，满足Cp(Bh;U)=min(|Cp(B1;U)-(m1+1)|,|Cp(B2;U)-(m2+1)|)的粗糙集Bh也更优。选择模型应考虑选择Cp值最小或是与mh+1最接近的模型[20]。在实际应用中，研究者通常以Cp值最小的模型为最优模型，如Olejnik等[20]、张新雨等[16]。本文认为，最小Cp值对应的Logistic模型最优，相应的粗糙集为所选择的最优粗糙集。Mallow’s Cp准则计算简单，在所有可能的规则子集中进行选择，是最优规则子集的有效选择方法。下文模拟结果显示，粗糙集的Mallow’s Cp选择算法能够很好地选择出较优的粗糙集。

算法1粗糙集的Mallow’s Cp选择算法

步骤1给定待选的两组粗糙集分类规则，针对一组分类规则，从中选取第一类的规则，定义新变量并赋值，记为类似地，另一组分类规则定义的新变量记为，其 中 ，i=1,2,…,n，m1、m2为新变量个数。将两组分类规则定义的新变量汇总，去掉重复的变量，变量全集记为

步骤2将分别作为Logistic模型的解释变量，决策属性yi作为Logistic模型的因变量，构建Logistic模型，分别记为模型1、2和3。计算模型1和2的残差平方和sse1、sse2以及模型3中方差的最大似然估计，依据公式计算模型1和2的Cp值。

步骤3比较所有粗糙集的Cp值，选择Cp值最小的Logistic模型。该Logistic模型所对应的粗糙集为最终选择的最优粗糙集。

在算法1中，步骤1选取第一类规则的时间复杂度为O(1)，定义并赋值新变量z1i和z2i的时间复杂度分别为O(m1×n)和O(m2×n)，汇总得到变量 z3i的时间复杂度为O(1)；步骤2的时间复杂度为O(1)；步骤3的时间复杂度为O(1)。因此算法1的时间复杂度取决于新变量个数m1和m2，为O(m1×n)和O(m2×n)中的较大值。

4 实验及结果分析

本章选用规模大小和属性个数各异的4个UCI数据集进行实验，验证粗糙集的Mallow’s Cp选择算法的有效性。实验环境为Intel®CoreTMi7-3770 CPU，4 GB内存，64位Windows 7操作系统的PC机，实验平台为R。主要考察数据集的分类问题，其中将数据集Abalone的非两分类决策属性，以9为界限合并为两分类（1表示决策属性值大于9，0表示决策属性值不大于9）。对每个数据集，从中随机抽取80%的数据作为训练集与测试集，用于粗糙集的构建与选择；剩余20%记为预留数据集，作为“新样本”，以粗糙集在预留数据集上的误判率为其泛化能力的考量指标。若所选粗糙集在预留数据集上的误判率最低，则认为择优算法选择了“正确”的粗糙集，否则，认为选择“错误”。共进行100次5折交叉验证，各数据集的具体信息见表1。针对4个数据集，表1第2列至第4列对应给出了训练集、测试集与预留数据集的容量，第5列给出条件属性的个数。

Table 1 Basic information of data sets表1 数据集的基本信息

对每个数据集，分别采用基于最大概率的粗糙集方法和基于贝叶斯的粗糙集方法，会得到两类不同的粗糙集分类规则。本研究采用粗糙集的Mallow’s Cp选择算法可从中选择出预测准确度更高的一类规则。每次模拟时，对数据分别采用两种方法构建粗糙集分类规则，利用第一类的规则定义两组解释变量，以决策属性为因变量拟合两个Logistic模型，以所有变量汇总并剔除重复后的变量拟合的Logistic模型为全模型，计算相应的Cp值。4个数据集的实验分别重复500次的结果如表2所示。表2第2至5列给出了分别采用误判率准则与Mallow’s Cp准则选择粗糙集的正确次数与错误次数，第6列给出了两种准则均选择正确的次数，第7列给出了Mallow’s Cp准则选择正确粗糙集而误判率准则未选择正确粗糙集的次数，第8列给出了误判率准则选择正确而Mallow’s Cp准则选择错误的次数。由表2可知，在500次重复过程中两种准则同时选择正确的次数都很多，除数据集Haberman外，正确率均超过72%。此外，对4个数据集，Mallow’s Cp准则选择正确而误判率准则选择错误的情况分别出现了69、113、91和68次，误判率准则选择正确而Mallow’s Cp准则选择错误的次数则分别为32、3、57和11次。后者的次数远小于前者，几乎均不超过Mallow’s Cp准则更好次数的一半，且在500次实验中占比均不超过11%。说明误判率准则更好的情况出现概率较少，多数情况下Mallow’s Cp准则的择优效果更好。出现误判率准则更好情况的主要原因是在两个粗糙集的分类精度相差较小但复杂度相差较大的情况下，若此时精度稍高的粗糙集对应的复杂度较高，则Mallow’s Cp准则倾向于选择精度稍低且复杂度低的粗糙集，而误判率准则倾向于选择精度稍高的粗糙集，从而出现误判率准则选择正确而Mallow’s Cp准则选择错误的情况。综上所述，Mallow’s Cp准则适用于粗糙集选择，相对误判率准则择优正确概率更大，择优效果更好。

Table 2 Comparison of 4 data sets(500 times)表2 4个数据集的对比情况（500次）

进一步考察两个粗糙集在测试集的误判率之差小于3%的情况，结果见表3。由表3可知，对4个数据集而言，两个粗糙集间的Mallow’s Cp准则相对差异大，容易选择出正确的粗糙集。而两个粗糙集在测试集的误判率之差小的情况较为普遍，分别达到471、282、160和192次，其中两种准则同时选择正确的次数分别为304、143、45和108次，Mallow’s Cp准则选择正确的次数分别达到373、254、83和139次，且出现69、111、38和31次Mallow’s Cp准则比误判率准则好的情况，明显高于误判率准则比Mallow’s Cp准则好的次数32、3、22和8次，此时Mallow’s Cp准则优于误判率准则，选择出具有强泛化能力的粗糙集的频率更高。Mallow’s Cp准则可以代替误判率准则择优粗糙集，是粗糙集择优的较好准则。

Fig.1 Average precision of two criterions in process of repeating 500 times(Abalone）图1 重复500次过程中两种准则的平均正确率（Abalone）

Fig.2 Average precision of two criterions in process of repeating 500 times(Breastcancer）图2 重复500次过程中两种准则的平均正确率（Breastcancer）

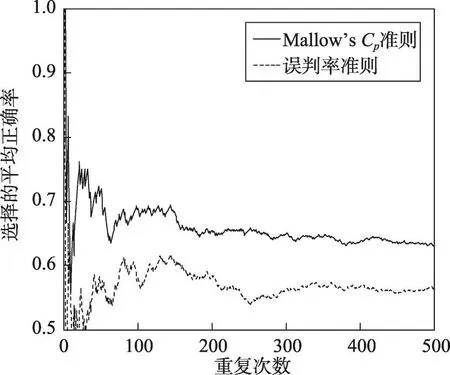
Fig.3 Average precision of two criterions in process of repeating 500 times(Haberman）图3 重复500次过程中两种准则的平均正确率（Haberman）

Table 3 Comparison of 4 data sets(when the difference of misclassification rates in test sets is small)表3 4个数据集的对比情况（在测试集的误判率差异小时）

针对4个数据集，从进行1次至重复500次的过程中误判率准则和Mallow’s Cp准则选择粗糙集的平均正确率的变化过程分别如图1～图4所示。每幅图的横坐标为重复次数，纵坐标为选择的平均正确率，虚线代表误判率准则的结果，实线代表Mallow’s Cp准则的结果。

Fig.4 Average precision of two criterions in process of repeating 500 times(Ionosphere）图4 重复500次过程中两种准则的平均正确率（Ionosphere）

图1～图4显示，在不同重复次数下，除数据集Haberman外，Mallow’s Cp准则和误判率准则选择粗糙集的平均正确率几乎都在70%以上。随着重复次数的增多，两种准则的平均正确率均趋于稳定。对4个数据集，误判率准则的平均正确率分别稳定在74%、73%、56%及77%左右，Mallow’s Cp准则的平均正确率分别稳定在81%、95%、64%及89%左右，均高于误判率准则。整个动态过程中，Mallow’s Cp准则的平均正确率普遍高于误判率准则，采用Mallow’s Cp准则更可能正确选择出泛化能力强的粗糙集。

5 结束语

实际问题中，粗糙集的泛化能力是评估粗糙集的关键，相应的粗糙集择优算法至关重要。本文引入Mallow’s Cp准则，构建粗糙集的Mallow’s Cp选择算法。新算法兼顾了粗糙集的分类正确概率与模型复杂度，能选择出具有强泛化能力的粗糙集，为粗糙集择优提供了新思路。实验分析结果显示，Mallow’s Cp准则与误判率准则选择强泛化能力的粗糙集的频率都较高。对误判率差异小的粗糙集，Mallow’s Cp准则选出泛化能力强的粗糙集的频率更高。