加权好友推荐模型链路预测算法*

钱付兰，杨 强，马 闯，张燕平

1.安徽大学 计算机科学与技术学院，合肥 230601

2.安徽大学 数学科学学院，合肥 230601

3.安徽大学 信息保障技术研究中心，合肥 230601

1 引言

网络已经成为描述形形色色复杂系统最重要的工具之一[1]，网络科学随着社交媒体和大数据的发展，以复杂网络和社交网络为目标的网络研究日新月异。网络中的链路预测问题主要是根据网络本身的拓扑结构和网络的外部信息寻找一些算法进行预测，估计网络中未产生连边的两点之间连接边的可能性[2]。链路预测作为网络科学中的重要研究内容，在众多现实问题中有着广泛的应用背景，业已成为横跨多个学科的核心科学问题。

无论是计算机领域的数据挖掘[3-4]还是社交网络中的朋友推荐[5-6]，无论是恐怖分子网络中的威胁发现还是生物领域中的蛋白质交互[7]，在实际的链路预测应用中，如何从现有的链路预测算法中选择较为合适的算法或针对具体网络结构和应用背景设计合理的算法，以取得较好的预测效果，是链路预测所要解决的首要问题。

常见的算法主要基于节点属性和网络局部结构进行链路预测。虽然利用节点属性等外部信息通常可以得到很好的预测效果，但是节点属性很多时候是难以获得的，即使获取也经常伴有噪声。相比而言，网络局部结构更易获得也更可靠[8]。因此近年来，基于网络局部结构的链路预测算法日益受到关注。

本文组织结构如下：第2章介绍了一些与本文有关的链路预测的研究工作。第3章主要介绍本文提出的链路预测算法。第4章是实验以及结果分析。第5章为结束语，总结本文的工作，对下一步研究进行展望。

2 相关工作

基于网络局部结构进行链路预测的算法有很多。其中，最简单的相似性算法是共同邻居算法[9]（common neighbor，CN），将两个节点间的相似性定义为共同邻居节点数。Adamic等人[10]考虑了节点间共同邻居的度，根据共同邻居节点的度为每个节点赋予一个权重值，提出Adamic-Adar，即AA算法。Zhou等人[11]受网络资源分配过程的启发，提出了资源分配指标（resource allocation，RA）算法，与AA算法有异曲同工之处。尹永超等人[12]考虑到不同邻居节点对两个终节点的影响，提出了CRA（common resource allocation）算法。基于网络局部结构的链路预测算法大体上可以分为如下几方面：

（1）融合局部结构性指标如聚类系数等提出新算法。

文献[13]受局部结构思想的影响，使用网络共同邻居节点的聚类系数直接表达网络的局部结构信息，提出的CCLP（clustering coefficient for link prediction）指标在预测缺失边的效果优于CAR（Cannistrai-Alanis-Ravai）指标。文献[14]利用三元闭包机制结合网络拓扑结构特性，提出了一种基于三元闭包的节点相似性链路预测算法并且提高了预测精度。文献[15]认为小度的邻居节点应该赋予较大的权值，在相似性度量中考虑所有节点和路径，提出了PNC（path and node combined approach）算法，并且提升了基于相似性的链路预测算法的性能，该算法好于节点依赖性和路径依赖性的方法。文献[16]考虑局部信息和偏好连接的影响，提出了CN+PA（common neighbor+preferential attachment）相似性指标，并且提升了链路预测算法的性能。

（2）刻画某种特殊局部特征并针对该特征提出新算法。

文献[17]首先刻画了网络中大多存在PWCS（nodes are preferentially linked to the nodes with weak clique structure）现象，即节点更偏向连接具有局部群落结构的节点。然后，该论文据此提出了一种朋友推荐模型——FR（friend recommendation）链路预测相似性计算指标，FR无论是AUC还是Precision都普遍优于传统指标。文献[18]从信息论的角度进行链路预测应用，链路预测中不同结构特征的贡献以信息的值的形式度量，并且提出了应用多种结构特征的信息论模型。基于此模型，该论文提出了NSI（neighbor set information）指标，优于一些经典的链路预测算法。文献[19]通过结构一致性指标刻画了一个网络的可预测性，并基于结构一致性提出了一种新的链路预测方法，取得了很好的效果。

（3）引入社会学/传播学等其他学科知识提出新算法。

文献[20]引入了3步之内为强关系，强关系引发行为的社会学知识，在考虑2步路径上的节点（共同邻居节点）对链接产生贡献的同时又考虑了3步路径上的节点的贡献，提出了CCN（cohesive common neighbors）相似性指标并且取得了较好的预测效果。文献[21]提出了一种假设，即每个节点吸引链路的能力不仅依靠其结构重要性，而且依靠其当前的流行度（活跃度）。然后，该论文提出了一种称为PBSPM（popularity based structural perturbation method）的新方法。在6个演化网络上的实验表明提出的方法在精度和鲁棒性上优于最新的方法。文献[22]定义了一种称为社团相关性指标的社团相似性特征，这一特征使用了不同社团间的直接信息和潜在信息。然后该论文为了预测缺失边，提出了一种基于社团相关性的新算法。实验表明提出的方法具有更有效的预测精度，社团相关性特征使得预测的时间复杂度更低。

在上面几种基于网络局部结构进行链路预测的算法中较为常见的是将网络局部特性和依据社会学/传播学中网络节点信息相结合，获得较为合理有效的链路预测策略，或针对某一网络结构特征构建适合该特征的链路预测算法。上述所提的FR算法基于好友推荐策略，中间人无差别将自身的好友介绍给目标用户，该过程与真实社交行为并不相符。因此本文利用真实社交网络好友推荐策略，中间人倾向于将自己更熟悉的人介绍给目标用户，提出了一种节点相似性度量指标。该指标结合局部特征描述并有效区分了用户节点之间影响力的不同，更适用于PWCS这类特定的局部群落结构。依据该指标提出的加权朋友推荐模型链路预测算法（link prediction algorithm based on weighted friend recommendation model，WFR）在12个公用数据上的实验结果表明其预测效果在AUC和Precision两个指标上都有较大的优势，在符合PWCS现象的网络中优势更为显著。本文最后通过对一般的人工数据上的实验，进一步讨论了WFR算法的适用范围。

3 算法描述

本文利用两个节点间共同邻居的数目来描述其连边的强弱。如果两个节点间的共同邻居数大于阈值α,则将这两个节点的连边称为强连接，否则就为弱连接。以图1中的无向图为例，这里选取α=3,图1①～③中节点A、B、C组成的连通子图可以转化为图1④～⑥简单情况。其中，粗线表示强连接边，细线表示弱连接边。

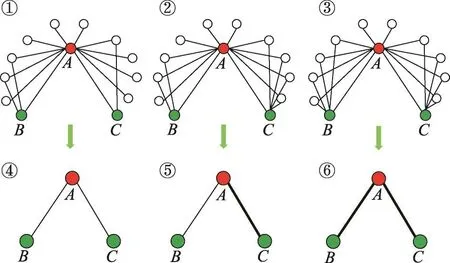
Fig.1 Transformation diagrams of 3 connected subgraphs图1 3种连通子图转换图

图2为包含3个节点的所有区分强弱连接的7个连通子图Ni,i=1,2,…,7（粗线表示强连接，细线表示弱连接）。P1、P2、P3分别是图2子图中有两条强连接边；图2子图中有一条为强连接边，另一条为弱连接边；图2子图中有两条弱连接边时，其余边相连接的概率。如式（1）～式（3）所示：

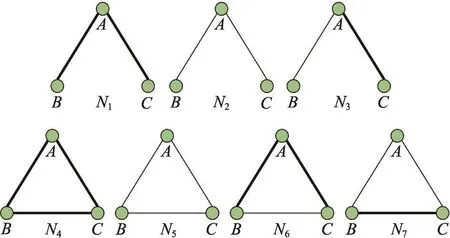
Fig.2 7 possible connected subgraphs with 3 nodes图2 包含3个节点的7个可能的连通子图

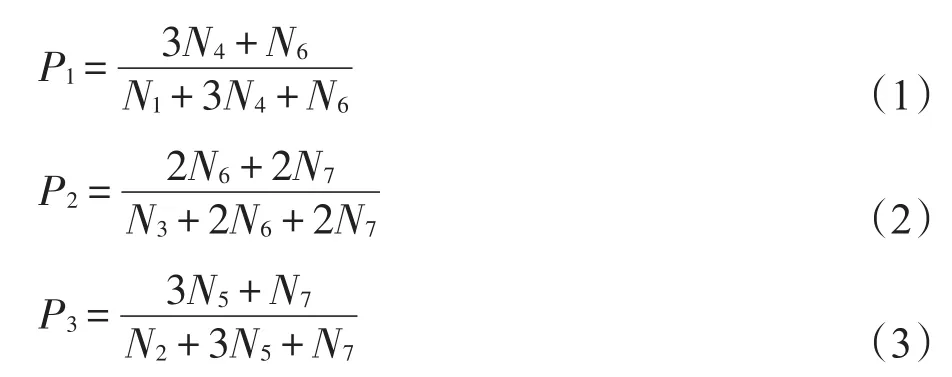
其中，P1中N4的系数为3，表示在两条强连接边的情形下，子图N4上取一条边为测试边的方式有3种。P2分子中N6的系数为2表示有且只有其中的一条为强连接边的情形下，子图N6上取一条边为测试边的方式有两种。以此类推得到式（1）～式（3）。

若P1＞P2且P1＞P3，说明网络节点间趋向于更紧密的局部连接，可以认为PWCS现象存在于网络中。若P1＞P2＞P3，可以认为PWCS现象是最明显的。当P1＞P3≥P2时，PWCS现象不明显。

基于PWCS现象提出的FR[17]算法通过式（4）计算节点l将自己的邻居节点i介绍给另一个邻居节点j的可能性。

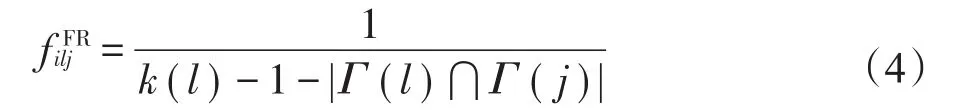
式中，l为中介节点，j为目标节点，i为候选节点，且j和i均是l的邻居节点。其中，k(l)为中介节点l的度，Γ(l)为节点l的邻居节点集合，|Γ(l)⋂Γ(j)|表示中介节点l与目标节点j的共同邻居节点数。分母中的“-1”是因为中介节点l不会推荐目标节点j给j,而“-|Γ(l)⋂Γ(j)|”表示当中介节点l推荐其相连的候选节点给目标节点j时，应该排除l和j的共同朋友。

由式（4）可得，分母为通过中介节点l推荐给目标节点j的所有候选节点i的个数，即中介节点l介绍给目标节点j的所有候选节点i的概率均相等，而实际情况中不同的候选节点i和中介节点l的亲疏程度存在着明显的差异。如图3所示，按照FR算法，候选节点1和节点4通过中介节点2推荐给目标节点6的概率是相同的，然而真实情况中节点4更容易被节点2推荐给节点6，即与中介节点l越相似的节点i，越容易被推荐给目标节点j。基于上述观点，本文提出一种基于加权好友推荐模型的链路预测算法，利用权重对候选节点和中介节点间的亲疏关系加以描述区分，称为 WFR（weighted friend recommendation）算法。设表示这种亲疏关系：

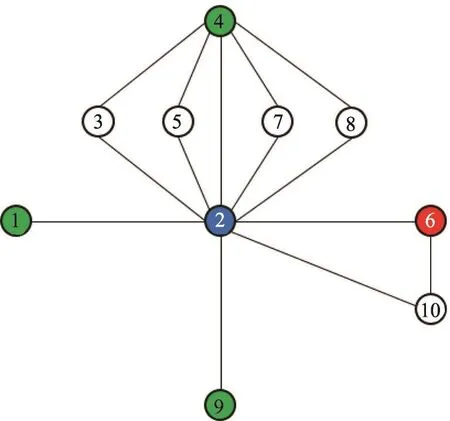
Fig.3 Asimple network图3 一个简单网络

节点i和节点j的相似性可以定义为：

WFR算法

输入：无向无权网络network。

输出：评价指标结果（AUC、Precision）。

开始

1.输入训练数据集。

2.统计被预测节点对(i,j)的共同邻居节点common_nodes。

3.根据式（6）计算被预测节点对(i,j)之间的相似度SWFRij。最后求得相似度矩阵SIM。

4.根据相似度矩阵SIM和测试数据集计算评价指标的结果。

结束

4 实验与结果

本文使用AUC（area under the receiver operating characteristic curve）[23]和精确度[24]（Precision）来评价算法性能，其中Precision排序列表长度为100。实验随机将原网络划分为训练集train和测试集test，其中训练集占90%，测试集占10%。

4.1 实验数据和对比算法

4.1.1 实验数据

本文使用Matlab软件作为实验平台，采用线虫的神经网络（C.elegans）[25]、爵士音乐家合作网络（Jazz）[26]、美国航空网络（USAir，http：//vlado.fmf.uni-lj.si/pub/networks/data/mix/USAir97.net）、蛋白质相互作用网络（Yeast）[27]、政治博客网络（PB）[28]、Facebook社交网络（FB，http：//snap.stanford.edu/data/）、电力网络（Power）[25]、路由器网络（Router）[29]以及4个食物链网络（FWFD、FWEW、FWMW、FWFW）（http：//vlado.fmf.uni-lj.si/pub/networks/data/bio/foodweb/foodweb.htm）。如表1所示，12个网络中，FWFD、FWEW、FWMW、FWFW、C.elegans、PB、Power和Router这8个网络中P1＞P2＞P3（用斜体表示），这些网络中PWCS现象更加明显。

4.1.2 对比算法

4.2 实验结果分析

为了有效验证WFR算法的性能和适用范围，实验由如下三部分组成。

（1）相似性指标的选取对算法的影响。

这部分实验通过在式（5）中代入多种相似性指标，验证WFR算法中加入权重指标的性能。

（2）权重比例变化对算法的影响。

考察权重对算法的影响，通过调节权重比例，观测WFR算法在AUC和Precision上的性能。

（3）人工生成的典型网络环境下算法的适用分析。

考察在人工生成的典型网络：一般的小世界网络和规则网络中，WFR算法的适用情况。

4.2.1 相似性指标的选取对算法的影响

式（5）中分别使用CN、AA、RA来计算中介节点和候选节点间的亲疏关系性权重Sil,分别为：

与之相对应的WFR算法分别记为WFR-CN、WFR-AA、WFR-RA，与一般的链路预测经典算法的比较结果如表2所示。从表2得到，WFR相对于FR和经典算法而言整体性能较好。尤其是在具有显著PWCS特性的8个网络（相关数据用斜线表示）：FWFD、FWEW、FWMW、FWFW、C.elegans、PB、Power和Router中，无论权重Sil如何计算，WFR算法均具有明显优势。其中WFR-CN这一相似性指标使用计算共同邻居的CN，更符合PWCS结构的定义，效果最优。表2中加粗字体表明效果最好。

图4（a）是对图3依据图1进一步抽象化后得到的简单连通子图。目标节点与中介节点连接可强可弱，因而图4（b）给出了另一种情形及其抽象化后的连通子图。根据式（1）～（3），图4（a）中边（2,4）为强连接，边（2,6）为弱连接，边（2,1）为弱连接，边（4,6）连接的概率为P2,边（1,6）连接的概率为P3;若要得到候选节点4与6连接的概率大于候选节点1与6连接的概率需要满足条件P2＞P3;同理，图4（b）中需要满足条件P1＞P2。显然WFR通过加权进一步强化了关系P1＞P2＞P3,在具有PWCS现象显著存在的网络中WFR可以得到较好的结果。

4.2.2 权重比例变化对算法的影响

为了进一步考察权重对预测效果的影响，式（6）进一步被改写为式（16）的形式，记为GWFR（generalized weighted friend recommendation）指标。

Table 2 Results ofAUC and Precision on 12 real-networks表2 12个真实网络上AUC、Precision的结果

图5给出了12种不同网络中随着α取值的不同，式（16）中GWFR相似性指标(Sil,Sjl)分别取CN、AA、RA时（分别表示为GWFR-CN、GWFR-AA、GWFRRA），与GFR指标在Precision上的比较结果。图5给出了P1、P2、P3取值的柱状图，由图5可以得到在符合P1＞P2＞P3的显著PWCS现象的网络中，不论α的取值如何，3种加权的GWFR算法效果都明显好于GFR算法。当α=1时，GWFR即为WFR，GFR即为FR。

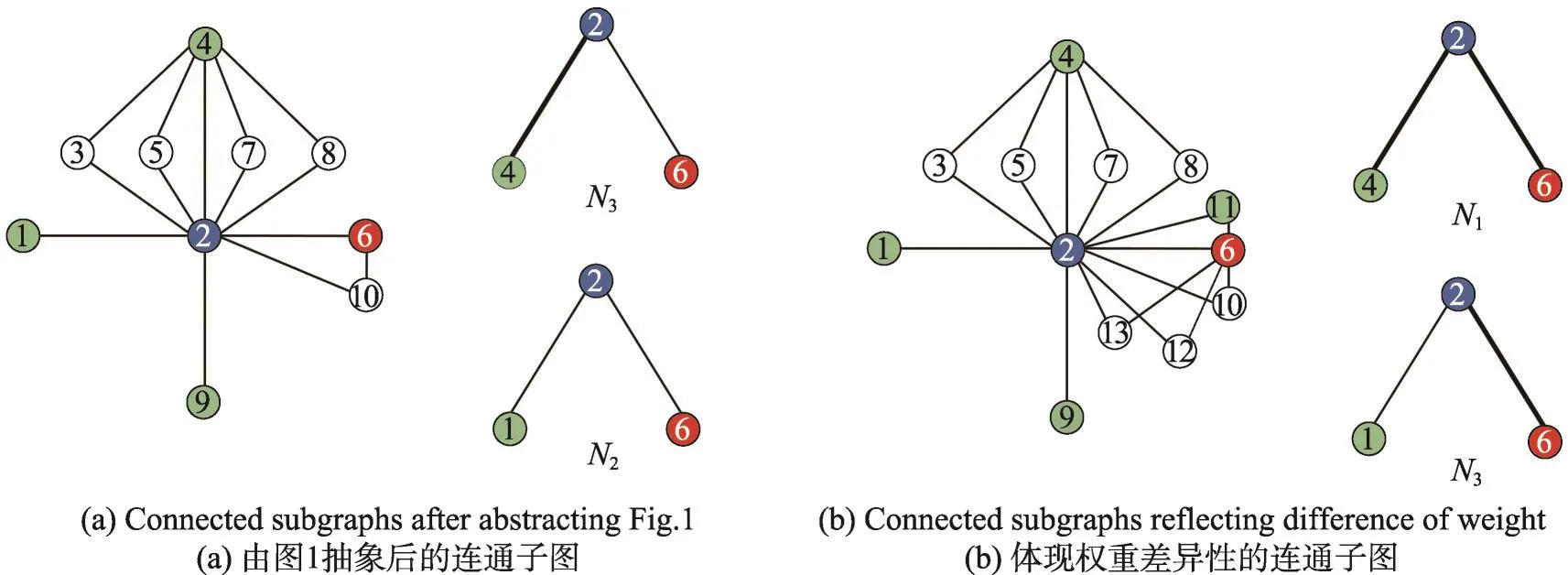
Fig.4 Analysis of effect of WFR algorithm on PWCS phenomenon图4 WFR算法对PWCS现象的影响分析

4.2.3 人工生成的典型网络环境下算法的效果

真实网络中的一些特征很难发现，提供一个适合所有网络的链路预测算法是非常困难的。本文考虑了两种典型网络生成模型——小世界网络和规则网络，对WFR算法的普适性进行考察。本文使用NW（Newman-Watts）小世界构造算法设置不同的参数生成了10个小世界网络，参数K的功能是调节网络的平均度，参数p的功能是调节网络的平均聚类系数，其特征信息如表3所示，本文设置网络的节点数N=1 000,其中每个节点都与它左右相邻的各K/2个节点相连，K是偶数。相应的AUC和Precision的结果如图6所示。

本文同样使用相应的规则网络构造算法生成了10个规则网络即最近邻耦合网络。其中每个节点都与它左右各K/2个邻居点相连，这里K是一个偶数。本文设置K值分别为2，4，…，20，网络的节点数N=1 000,网络的特征信息如表4所示，从net1到net10，网络由稀疏到稠密。相应的AUC和Precision的结果如图7所示。

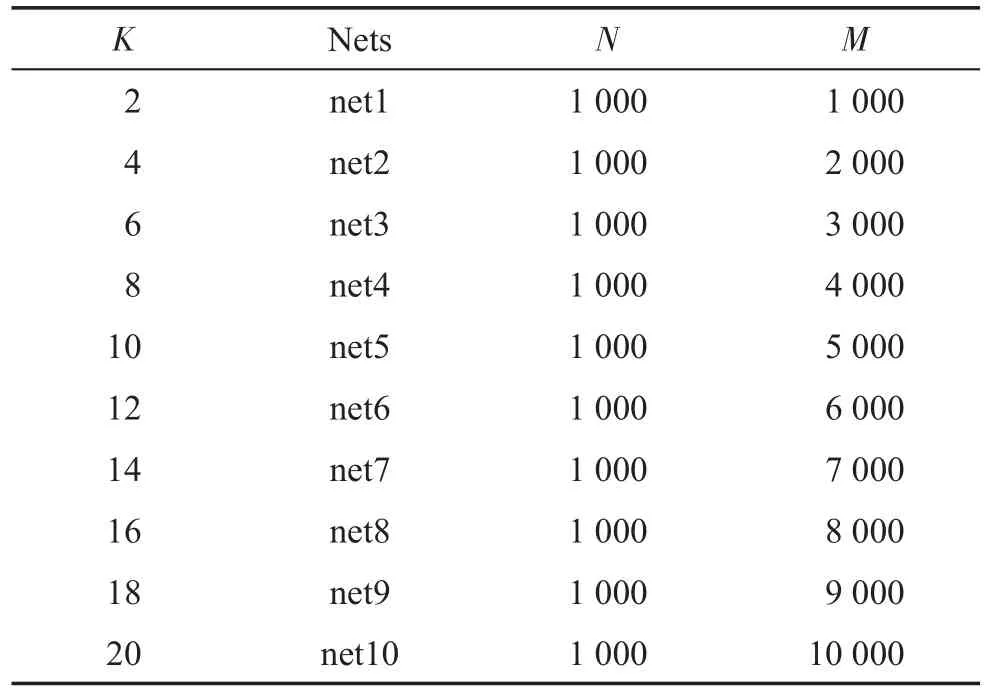
Table 4 ParameterKand features of 10 regular networks表4 参数K和10个规则网络的特征

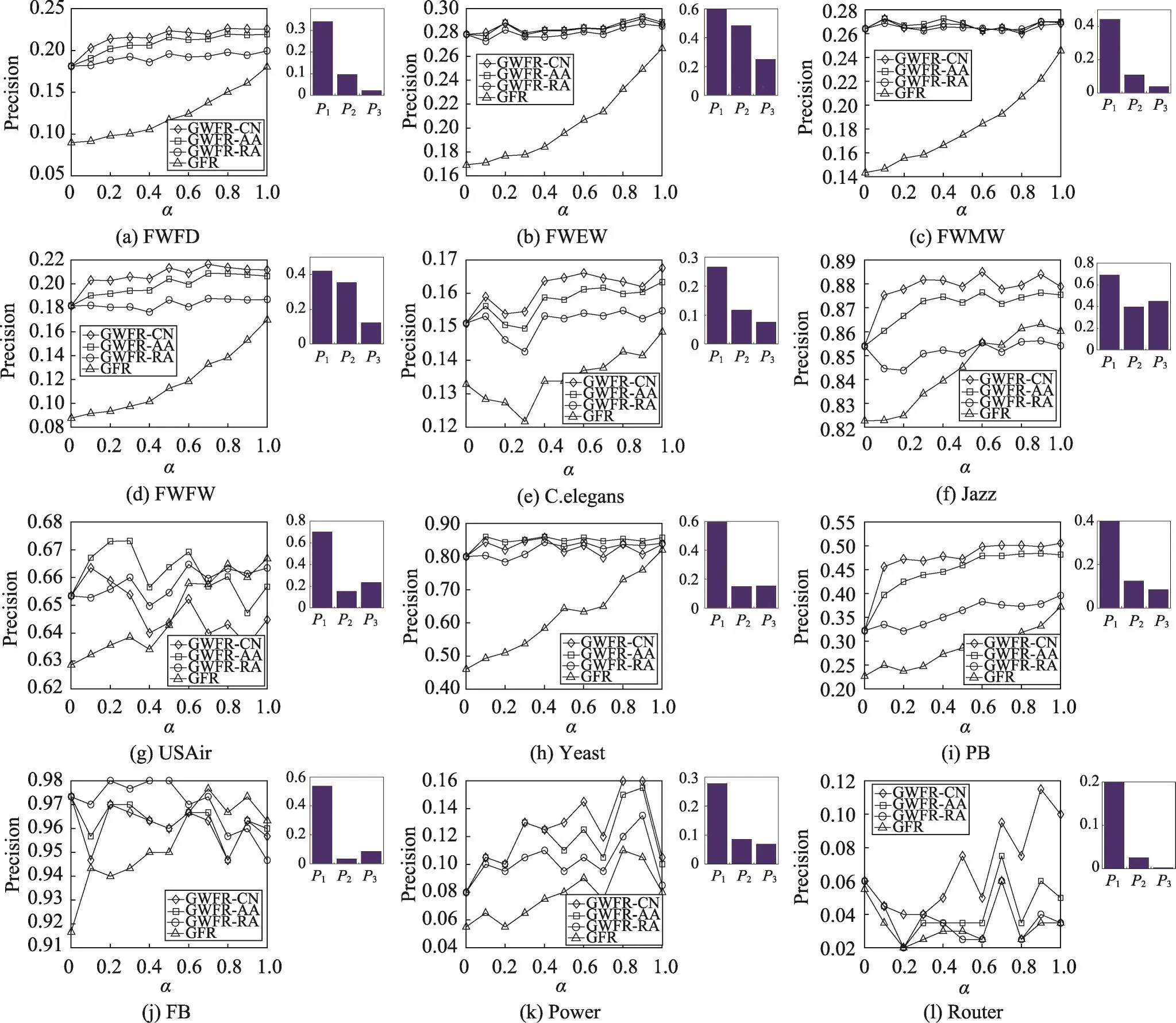
Fig.5 Relationship between Precision andα图5 Precision与参数α之间的关系

从图6、图7中可以看出，总体而言，无论在小世界网络还是规则网络中，本文提出的WFR算法与FR算法相比在网络更为稠密的情况下，WFR算法效果要明显优于FR算法。而相对稠密的网络具有局部群落特点的PWCS现象也更为明显，因而WFR算法优于FR算法。

4.3 算法时间复杂度分析

在基于共同邻居的链路预测算法中，计算节点对的共同邻居的时间复杂度为,表示网络的平均度。AA、RA两种算法与CN算法有着相同的计算过程，因此与CN算法的时间复杂度相同。FR、WFR算法预测过程与基于共同邻居的其他算法的预测过程相同，即与CN、AA、RA算法的预测结果相同。如CN算法的时间复杂度为O(n2×k)。因此WFR-CN算法的时间复杂度为O(n2×k),保证了该算法的时间复杂度不大的情况下，取得了比CN、AA、RA、FR算法更优的预测效果。

5 结束语

WFR算法是一种基于加权朋友推荐的链路预测算法，该算法利用社交网络好友推荐策略，中介人倾向于将自己更熟悉的人介绍给目标用户的特点，结合局部特征构建节点相似性度量指标。WFR有效区分了用户节点之间影响力的不同，更适用于具有局部群落结构现象（PWCS）特征的网络环境。与CN、AA、RA、FR这些基于共同邻居的链路预测算法相比，WFR算法在保证时间复杂度大致相同的情况下，整体上取得了较好的预测效果。本文研究的链路预测算法主要考虑共同邻居节点和局部结构特征，对网络的描述刻画仍不够全面。下一步的研究工作主要有两方面：一是如何利用更多的网络结构信息来提高链路预测的效果；二是如何针对具有不同特征的网络结构提出合适的高效链路预测算法。

Fig.6 AUC and Precision of FR and WFR-CN in NW small world networks图6 小世界网络中AUC、Precision下的FR、WFR-CN指标

Fig.7 AUC and Precision of FR and WFR-CN in regular networks图7 规则网络中AUC、Precision下的FR、WFR-CN指标