关于草原合理放牧的数学模型及其定性分析
——以乌兰布统大草原为例
王崇奂,张乐予,陈晓玥,王秋爽
(吉林师范大学 数学学院 ,吉林 长春 130012 )
0 引言
假设在同一生境(乌兰布统大草原)中,短期内捕食者(牛、羊等食草性动物)与食饵(草原上的牧草)的数量不受突发状况如:疫情、生物入侵、自然灾害等影响。由于动物出生、死亡,牧草生长、枯萎,两种群的数量都会随时间的变化而变化.本文运用数学的方法建立并研究两种群数量的动态系统。
在同一生境中的捕食者和食饵种群数量关系的数学模型[1]如下:
(1)
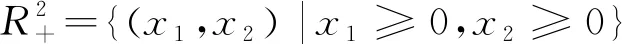
1 系统分析
模型(1)右端函数为0时,解得系统共有四个平衡点:
其中
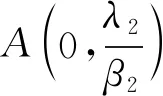
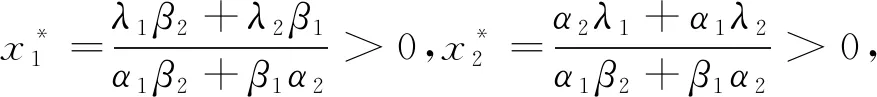
(2)
令F1(x1,x2)=0;F2(x1,x2)=0,
定理1(零点定理):若函数f(x)是闭区间[a,b]上的连续函数,且f(a)与f(b)异号(即f(a)·f(b)<0),那么函数f(x)在开区间(a,b)内至少有一个零点,即至少存在一点ξ,ξ(a<ξ 定理3当Δ=α1β2>0时,系统(2)的一切由第一象限出发的轨线是正向有界的. 在这些集合区域里,分别所对应的系统(2)的向量场方向变化.如图1. 图1 系统(2)的向量场 由各区域方向场分析:以及平衡点的唯一性和无环性可得:系统(2)的一切由第一象限出发的轨线是正向有界,系统(1)的正平衡点C(x*,y*)是全局渐近稳定的[4]. 生态系统的平衡稳定指的是生态系统的相对平衡,它是由生态系统自身的内部平衡与外部平衡所构成的,并且是一种动态性质的平衡[5].每个生态系统都具备着自身的一定范围内的弹性与可塑性,拥有着适应外来干扰的一定限度的反馈能力.本文通过对系统(i)的分析讨论,可以找到乌兰布统大草原上的捕食者(牛、羊等食草性动物)和食饵(牧草)最适合生存的数量C(x*,y*).由于两种群之间存在捕食关系,可以通过调节捕食者或食饵数量来维持生态平衡[6],即:当食饵种群(牧草)繁殖较快或生长较为茂盛时,我们可以人为引入捕食者(牛、羊等食草性动物)来控制其增长速度,既不会资源浪费还可以带来一定经济效益,但如果捕食者过量又会导致放牧过度食饵枯竭,也不利于捕食者生长,此时需要对捕食者进行适量捕杀.只有两种群数量达到C(x*,y*)时,才可以达到生态平衡稳定[7],从而实现保护牧草资源,又实现牧业经济最大化的目的.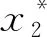
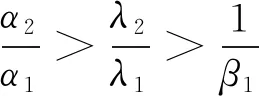
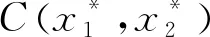
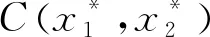
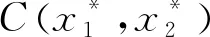
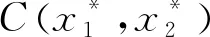
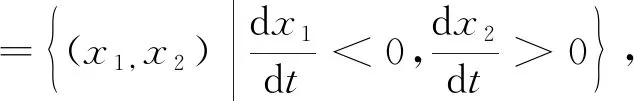
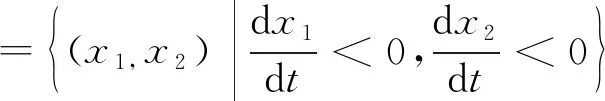
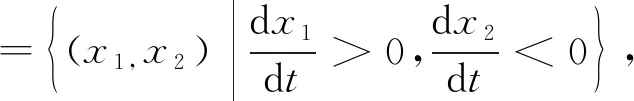

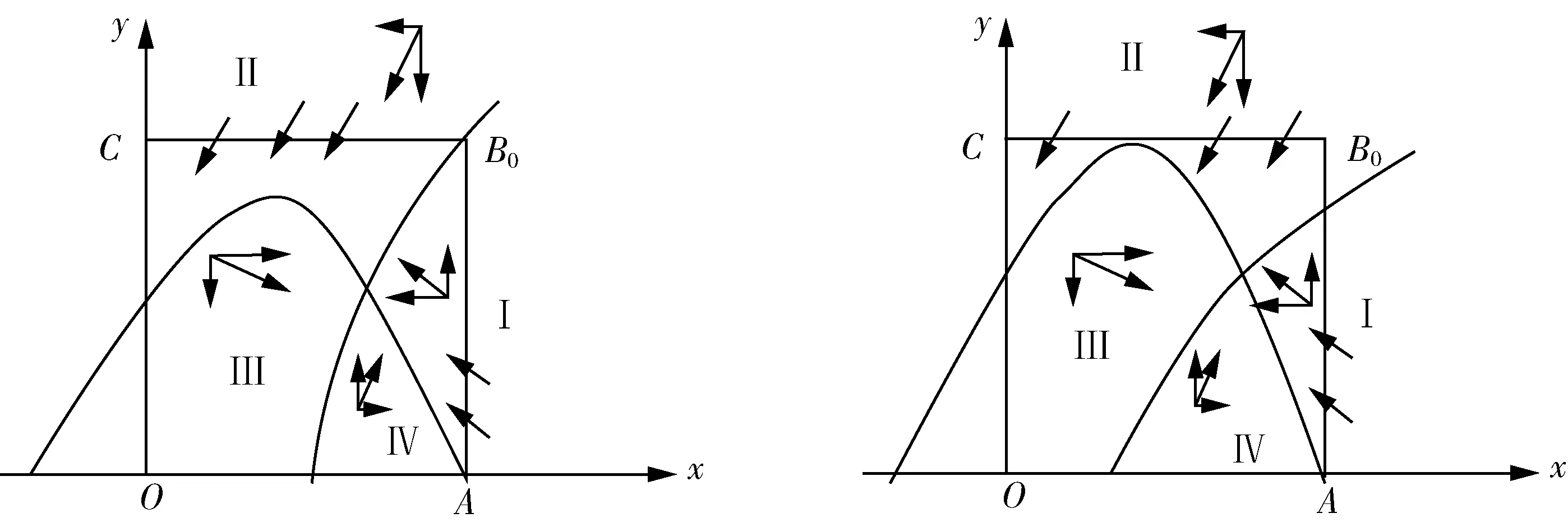
2 生物意义

