实解析函数空间上两个Phragme′n-Lindelöf条件的等价性

张 婧,曹 峰，王 光

(1.太原学院 应用数学系，太原 030001；2.山西大学 计算机与信息技术学院，太原 030006；3.山西大学 数学科学学院，太原 030006)

0 引言

自Hömander在1973年开创性地应用代数族V上Phragme′n-Lindelöf条件研究常系数线性偏微分算子P(D)解的性质以来[1]，许多学者应用代数族V上Phragme′n-Lindelöf条件来探讨常系数线性偏微分算子P(D)解的情况，如R.Meise、吴密景等学者研究了常系数线性偏微分算子P(D)的右逆存在性[2-3].在此基础上，众多学者研究了常系数线性偏微分算子P(D)的扰动问题[4-6]；乔蕾等学者研究了广义带形区域中的Phragme′n-Lindelöf型定理[7]；Ederson等学者证明了完全非线性方程的一个Phragme′n-Lindelöf定理[8].因此，进一步研究代数族上的Phragme′n-Lindelöf条件，明确各种Phragme′n-Lindelöf条件之间的关系[9],尤其是研究与常系数线性偏微分算子P(D)解存在性密切相关的Phragme′n-Lindelöf条件，才能在处理实解析函数空间上P(D)满射性等相关问题时，可以通过选择适当的Phragme′n-Lindelöf条件让研究过程更便捷.

1 基本概念

定义1.1[9]通常意义下多重次调和函数的定义

(1)设u为定义在中开集Ω上取值于[-∞,+∞)的函数，且满足

(α)u是上半连续的；

(β)对每个紧集K⊂Ω和每个在intK(K的内点集)中调和在K上连续的函数h，若在∂K上有u≤h，在K上就有u≤h成立.

则称u为Ω上的次调和函数.

(2)设u为定义在n中开集Ω上取值于[-∞,+∞)的函数，且满足

(α)u是上半连续的；

(β)对n中每个z和w，函数τ→u(z+τw)关于τ∈为次调和的.

则称u为Ω上的多重次调和函数.

代数族V上的多重次调和函数的定义

(α)u是局部上有界的；

(β)u在Ω中V的正则点Ωreg上按通常意义是多重次调和的；

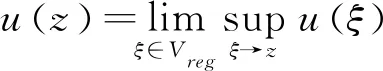
则称u在Ω上是多重次调和的.V上多重次调和函数的全体记作PSH(V).

定义1.2[9]支撑函数

设K⊂n是紧凸集，则hK(ξ)=sup{x*ξ:x∈K}表示K的支撑函数.

定义1.3[9]HPL(Ω)条件

若对每个紧凸集K⊂Ω，存在紧凸集K′⊂Ω及δ>0，使得对Ω的每个紧凸集K″⊂Ω及η>0，都存在常数η′>0，使当u∈PSH(V)满足条件1)、2)时必满足条件3)，则称代数族V满足HPL(Ω)条件.

1)u(z)≤hk(Imz)+δ|z|z∈V

2)u(z)≤hk″(Imz)+η′|z|z∈V

3)u(z)≤hK′(Imz)+η|z|z∈V

定义1.4[9]HAPL(Ω)条件

将定义1.3中的多重次调和函数u换成u=log|f|，其中f为n上的整函数，则称代数族V满足HAPL(Ω)条件.

符号说明[10]：

z=(s,w)=(z1,…,zn-k,w1,…,wk)∈n-k×k

映射π:z=(s,w)→w是V到k的满射.

B=B(0,ε(z))={τ∈k:|τ|<ε(z)}

z(τ)=(sj(w+τ),(w+τ))∈V∩Ω

|z(τ)-z|<1

2 主要结论

引理2.1[10]1)若u是V∩S0上多重次调和函数，则对所有z∈V∩S0，u(z)≤max{u(ζ) |ζ∈VS0,|ζ-z|≤1}

2)存在常数ε1，c1，使得对z=(sj(w),w)∈VS0,ε(z)=ε1(1+|w|)-c1有：

z(τ)=(sj(w+τ),w+τ)∈Ω

B(z(τ),8ε(z))⊂Ω

|z(τ)-z|≤1 对一切|τ|≤8ε(z)

引理2.2[10]设0<θ<1，则存在常数c2>0，对所有V上正则点处的多重次调和函数u，有0≤u(z)≤ρ|z|z∈V ；对所有z=(sj(w),w)∈Vs0，存在B的子集E使得下列结论成立：

(1)|E|≤|B|max(1,ρ)(1+|z|)-2

(2)对∀τ∈BE，存在Cn上的整函数fτ,log|fτ(z(τ))|≥θu(z(τ))-c2log(2+|z(τ)|)

(3)对∀ζ∈V，有log|fτ(ζ)|≤max{u(ζ′)|ζ′∈V,|ζ′-ζ|≤1}+c2log(2+|ζ|)

定理2.3代数族V满足HPL(Ω)条件的等价条件是V满足HAPL(Ω)条件.

证明：必要性

根据HPL(Ω)条件和HAPL(Ω)条件的定义，代数族V满足HPL(Ω)条件时显然HAPL(Ω)条件也成立.

充分性

若代数族V满足HAPL(Ω)条件，设u是代数族V上的多重次调和函数，并且V满足HPL(Ω)条件中的1)、2)：

1)u(z)≤hk(Imz)+δ|z|z∈V

2)u(z)≤hk″(Imz)+η′|z|z∈V

不妨设u≥0.

对于u=log|f|，f为Cn上的整函数从而log|f|为V上的多重次调和函数.由于代数族V满足HAPL(Ω)条件：对任意的紧凸子集K⊂Ω，存在紧凸子集K′⊂Ω及δ>0，使得对任意紧凸子集K″⊂Ω和η>0，存在常数η′>0，使得下列1)、2)成立时3)也成立.

1)log|f|≤hk(Imz)+δ|z|z∈V

2)log|f|≤hk″(Imz)+η′|z|z∈V

3)log|f|≤hk′(Imz)+η|z|z∈V

所以，只须证明对任意的多重次调和函数

即可(0<θ<1).

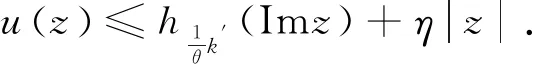
根据多重次调和函数的平均性质

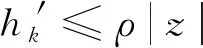
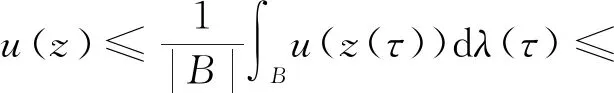
由引理2.2得

fτ(ζ)满足HAPL(Ω)条件中1)、2)

1)log|fτ(ζ)|≤hk(Imζ)+δ|ζ|ζ∈V

2)log|fτ(ζ)|≤hk″(Imζ)+η′|ζ|ζ∈V

从而fτ满足log|fτ(ζ)|≤hk′(Imζ)+η|ζ|ζ∈V

根据引理2.2中对fτ的估计可知

其中c与θ、η、c2、ρ、V有关.

于是u(z)≤ρ2+sup{u(z(τ))|τ∈BE}≤

(η1与c、ρ、θ、η有关，且η1>η)

定理2.3证明了代数族V满足关于一般多重次调和函数u的HPL(Ω)条件和代数族V满足关于特殊的多重次调和函数u=log|f|的HAPL(Ω)条件是等价的.由于常系数线性偏微分算子P(D)在实解析函数空间上的满射性又可用HPL(Ω)条件来刻画，因此，在研究常系数线性偏微分算子在实解析函数空间上解的存在性等问题时可以通过选择适当的HPL(Ω)条件，这无疑为常系数线性偏微分算子的研究另辟蹊径.