由圆围成两个圆锥体积和的最大值的讨论

赵 虹 王丽新

(长春师范大学数学学院 130032)

遇到这样一个问题，在一个圆上剪去一个扇形做成一个正圆锥，发现剪去的扇形圆心角太大或太小时做成的圆锥体积都较小，那么一个很自然的问题是剪去的扇形圆心角多大时做成的圆锥体积最大？这个问题在中学教学过程中也是有可能被学生问到的问题，这个问题利用均值不等式或高中的导数知识不难解决，但余下的扇形也能做成一个圆锥，若问剪去的扇形圆心角多大时做成的两个圆锥体积和最大，却发现是一个稍复杂的问题.本文将对此进行讨论.

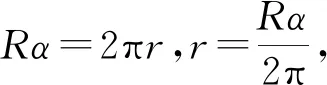
由以上讨论易知余下的扇形做成的圆锥的体积为

则这两个圆锥的体积和为

V=V1+V2

下面讨论函数

的最大值.

记1-x=y，则此函数的最大值转化为求二元函数

在条件x+y=1下的最大值.

利用条件极值的拉格朗日(Lagrange)乘数法[1]，设

令

整理得

或

(1)式两边平方可整理为

9(x6-y6)-3(3x2y2+4)(x4-y4)+4(3x2y2+1)(x2-y2)=0，

(x-y)[9(x5+x4y+x3y2+x2y3+xy4+y5)-3(3x2y2+4)(x3+x2y+xy2+y3)+4(3x2y2+1)(x+y)]=0,

或

(x-y)[9(x4(x+y)+x2y2(x+y)+y4(x+y))-3(3x2y2+4)(x2(x+y)+y2(x+y))+4(3x2y2+1)(x+y)]=0,

注意到x+y=1，则上式可继续化为

(x-y)(9(x4+x2y2+y4)-3(3x2y2+4)·(x2+y2)+4(3x2y2+1))=0，

又由x+y=1，则

x2+y2=(x+y)2-2xy=1-2xy,

x4+y4=(x2+y2)2-2x2y2

=1-4xy+4x2y2-2x2y2

=1-4xy+2x2y2.

(1)式可最终整理为

(x-y)(18x3y3+30x2y2-12xy+1)=0，

则x-y=0或18x3y3+30x2y2-12xy+1=0.

又

18x3y3+30x2y2-12xy+1=0

为关于xy的三次方程，利用三次方程的求根公式[2]得三个根为

由

舍去这个根，另两个根和x+y=1联合解得

(其中k1=(xy)1,k2=(xy)3.)

对应的

f(x1)=f(x2)

f(x3)=f(x4)

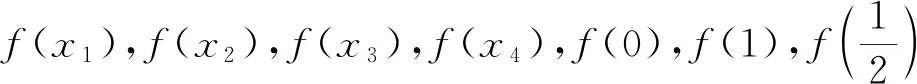
(2x-1)(18x6-54x5+24x4+42x3-42x2+12x-1)=0

注3若对一般的(圆)扇形(不一定为整个圆)，如何分成两个或多个扇形使围成的两个或多个圆锥体积和最大，也是一个值得讨论的问题.