以匹配课堂的数学文化作为探究的抓手
孙晓红
【摘要】依据史海寻根——课堂匹配——活动支撑——效果检测——拓展延伸这四大关键环节,让数学史从历史知识形态走向教育教学形态融入小学数学课堂。基于数学史实去琢磨数学家曾经走过的弯路、碰到的认知障碍,才会对数学教育有新的感悟,才能有效实现数学文化在课堂教学中的有机融入,有效发展理性思维。
【关键词】数学文化 课堂 探究 抓手 理性思维
数学学科本身有着漫长的发展之路,每一个定理,每一个分支,每一段历史,每一个国家,每一个数学家等都有着鲜明的历史印迹。能沉淀下来的,保留至今的都是宝贵的财富。学生在课堂上遇到的学习障碍正是数学家曾经遇到过的。我们学习数学的过程,应该和人类认识数学的过程一样。我们应该按照数学发展历史的顺序学习数学,体会数学发展的每个瓶颈,体会先有直观思维再给出形式化描述的艰难。只有理解人类如何获得某些事实或概念的知识,我们才能对学生应该如何获得这样的知识做出更好的判断。
学情调研(问题调研+访谈)
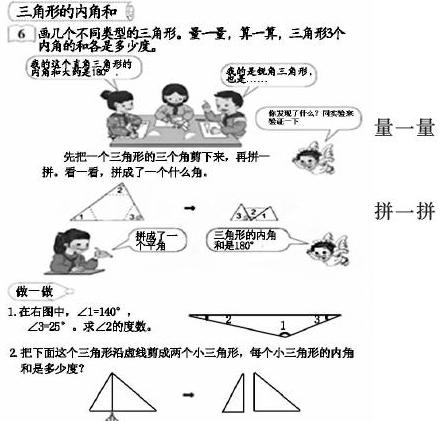
1.三角形内角和是多少度?
2.你是怎样得出来的?(量、拼、折)
3.你当时得到的每次刚好都是180°吗?你确信你拼的一定是一个平角吗?
4.你现在确信三角形内角和一定是180°吗?
从调研结果和访谈看,有一些学生对任意三角形内角和是180°存有质疑。从E、F两个班的数据来看没有质疑,调查了解到這个教师比较权威化,对学生要求也严格,他所带的学生必须听话,所以学生从来不质疑。探究时最后一个角很多学生是算出来的,并没有真正去量。 其他班也存在这样的情况,当孩子在课前从教师、书本等不同渠道得到这一结论时,他们的做法是什么?(1.更改角的度数,凑180°;2.量2个角,第三个是算出来的)因为四年的学习经验就已经告诉学生,教师和课本永远是对的。
更改数据背后反映的是什么?学生不质疑、不求真的学习态度与习惯!对于前面四个班的还有质疑火花的孩子们,如果我们置之不理,他们在若干年以后是否也就成了前一批直接更改数据的孩子呢?对这些存在质疑的孩子,我们应该如何帮助他们呢?
比较有意思的是,同样的问题,在经历了一年的成长之后,对五年级学生做追踪调研,数据出现了变化。
追踪调查D班学生,这节课的内容是苏教版四年级下册,这学期他们上升到五年级,同样的上面4个问题,统计结果如下:
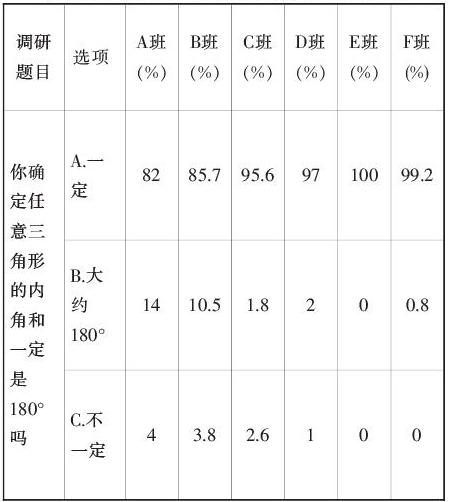
随着年龄的增长,一句“因为有误差,大家测量的不够准确,正确的应该是180°”,一直是孩子心中的一个结,有的孩子认为,自己已经尽心尽力的测量,已经够准确了,“误差”这个词的理解,学生心理接受是有一定困难的。
思考:
1.测量三个角,然后相加,是谁想出来的?
2.内角和是180°的结论是谁发现的?
3.教学中怎样引导学生去发现这个结论?
4.初中几何证明添加辅助线是怎么想到的?
5.怎样给学生解释小学测量有误差?
……
不鼓励学生问什么,不讲证明,数学就失去了灵魂!是否可以在课堂上引入小学生能理解的更为严谨的证明呢?利用符合学生心理特点的理性思维来避开“误差”带来的尴尬,使得实验几何向论证几何迈出一小步。
依据笔者课堂实践总结的经验:史海寻根—课堂匹配—活动支撑—效果检测—拓展延伸这四大关键环节,让数学史从历史知识形态走向教育教学形态融入小学数学课堂。
史海寻根:三角形内角和的发现与证明—泰勒斯、毕达哥拉斯、帕斯卡、欧几里得……
通过与古人的深入“交流”体验,运用古人解决问题的方式、方法把“实践操作”和“演绎推理”结合起来,让孩子了解数学的本质,培养理性精神,触摸数学的灵魂。构思出如下课堂结构:
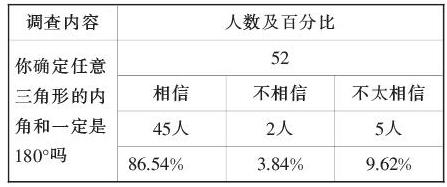
基于以上分析,制定如下目标:
1.经历从特殊到一般的推算三角形内角和的方法,质疑结论的正确、真实,以及方法的科学性,培养学生崇尚真理、探求真知的科学思维和精神。
2.触摸数学历史,感受数学文化,挑战数学家,养成勇于挑战,能做和数学家一样的事,提升探究的勇气。学习主动探究新知的方法,了解转化迁移的数学思想,发展合情推理和演绎推理能力。
3.通过数学拓展,将数学知识与“红色文化”有机融合,提升学科育人功能。
实践操作
通过课前的一个话题:老师和老黄牛比,有什么不同?从学生的回答中引出“问”与“思”,本节课从问与思开始,经历问什么,思什么,最后明白怎么问,怎么思。在这个过程中体验科学的质疑、求真之道,这是课堂的明线。然后再把四个关键环节有机融入“推理+计算=推算环节”多种方法进行说理,这个活动的放手使得学生在探究中呈现出了异彩纷呈的创新。现撷取几个精彩片段:
一、引导质疑、聚焦问思
师:运用这些方法,得出的三个内角的和都是180°吗?为什么?
依据学生的问题:三个内角的和到底是不是180°?量的时候有多有少啊?拼的也不见得平,所以不是很准确!为什么要让我们往一起拼,和是怎么想到的?……相机板书:180°?、不准确、怎么想到和?(其实这是对知识的三种质疑——结果的正确性、方法的科学性、知识的来源)
二、匹配课堂、推算说理
(一)推算活动
师:用这些方法得出的三角形内角和是180°并不能使我们信服,看来我们需要寻求另外的途径,也就是思考怎样解决(板书:怎样解决)。其实,关于内角和是多少度我们可以从前面的一些经验中得出,比如正方形的内角和是多少度?
生:360°。
师:你怎样得出的?
生:每个角都是90°,4×90°=360°。
师:听出来没有,就刚才这位同学所说的,其实就是推理+计算(板书:推算)。通过推算,得出正方形的内角和是360°,你确信吗?(确信)这就是数学中的讲道理,通过推算,以理服人。
师:你觉得哪类三角形的内角和与正方形最有关联?(等腰直角三角形)你能像刚才这样推算出等腰直角三角形的内角和吗?
学生想出从对角线分割360°÷2=180°
师:推理加计算,你们认可这个结论吗?
我们这时候能不能下结论说,所有任意直角三角形的内角和是180°?

生:不能,目前只能得到等腰直角三角形的内角和是180°。
师:如果要得到所有直角三角形内角和是180°,还得研究谁?它又会与哪个图形联系紧密呢?
生:还得研究一般的直角三角形,它与长方形联系紧密。我们也可以把长方形分割成两个直角三角形,然后用360°÷2=180°得出一般的直角三角形内角和是180°。

师:这时,我们可以下结论说(学生说出,任意直角三角形内角和是180°)。
要想得出任意三角形内角和是180°,你觉得还得研究哪些三角形?
出示研学单:
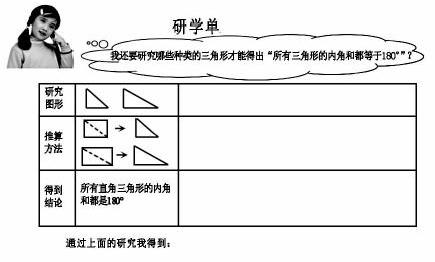
这个研学单与一般的学习单不同的地方在于,一般的学习单是老师设计好的学习过程,学生只需按要求操作就可,思维含量低。这个研学单是放手让学生自己设计下一步研究的方向,主动探究、思考,更利于学生的素养落地。而由正方形开始到最后探究得出任意三角形内角和是180°的由特殊到一般的思维过程,正是当年12岁的帕斯卡得出的方法。据说他是用炭块在墙上完成的。这个环节我不是像贴标签式的讲述一段历史,而是通过设计匹配的活动,让学生重走数学家的道路,体会能做和数学家一样的事。当学生经历由一般到特殊的过程,最后得出结果,笔者说出,刚才我们探究的过程就是神童数学家帕斯卡12岁发现的方法,你们才11岁,比他还厉害以后肯定会成为数学高手的时候,学生的那种自豪感,对数学探究的激情洋溢于表。
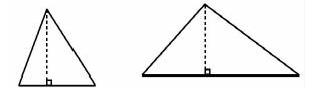
孩子们大多通过做高,转化为两个直角三角形,180°×2=360°,360°-90°×2=180°推算出锐角三角形、钝角三角形,最后得出任意三角形内角和事180°。由于放手让学生研究,汇报中的那些有问题的学生通过其他学生的质疑、互辩,精彩不断。
2、体验活动
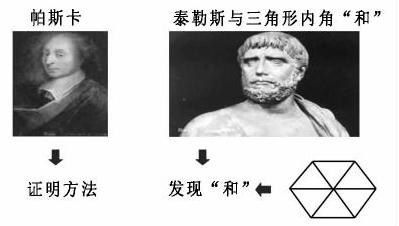
师:开始的时候有同学问道,和是怎么想到的?據说与希腊的大数学家泰勒斯有关,他有一次用等边三角形砖铺地的时候发现了等边三角形内角和是180°。你们能利用下面的图说说为什么吗?

善于思考的泰勒斯想,其他的三角形会是怎样呢?
请同学们以四人小组为单位,分别用六个同样的等腰三角形或六个同样的不等边三角形来拼图,感受泰勒斯当年的探究“三角形内角和为180°”的发现过程。
学生通过拼图、说明,重温了泰勒斯当年的过程。以下为学生部分作品。
数学文化的有机融入,一定要有匹配的活动,让学生去体验,而不是一句口号,而且这样以文化为暗线的活动是学生探究的有效抓手。
三、拓展延伸、效果检测
(一)拓展
师:同学们,我们刚才的拼图还有这样的惊喜呢!你们看:
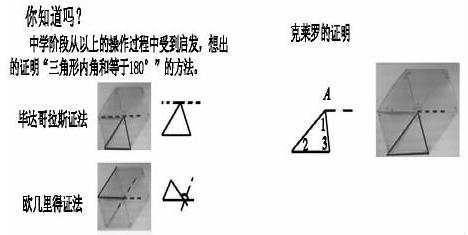
为学生呈现初中论证的源头,体会知识的链接,为后续的学习铺好道路。

(二)检测
1.变与不变
仔细观察在千斤顶下放的过程中,三角形的内角是怎样变化的?其中什么没变?

(2)算一算
红领巾的这个角师多少度
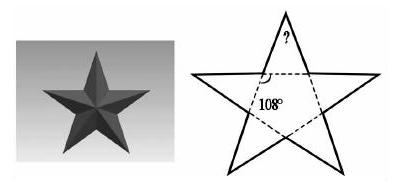
五角星的这个角是多少度?
本节课学生经历了数学发现的理性道路:特殊到一般归纳思维方式,学会了以理服人。学生学习数学的过程是数学史的快进,怎样能自然的融入,达到润物细无声的有机匹配,笔者上面的实践提供了一种可参考的途径即:史海寻根—课堂匹配—活动支撑—效果检测—拓展延伸 。以匹配的数学文化为探究的抓手,实践证明学生喜欢上这样的课,学生在这样的课中素养提升效果明显。

