一道原创试题的编制历程与思考——以直线与圆的位置关系为例

江苏

随着考试理论的不断发展和命题技术水平的不断提高，高考命题也在与时俱进，新背景的试题在高考中层出不穷，这些试题虽然不难，但学生往往无法应对，造成这种现象的主要原因是在平时的教学活动中，教师大都采用的是现成的陈题，一旦出现背景新颖的试题，学生缺乏应对体验及策略.因此，适当原创试题，并运用在平时联考中，是提高学生应变能力的重要途径.在一定程度上，一道好的原创试题不仅可以引导教师改进教学方法，更能唤起学生学习数学的激情.

事实上，命制试题早已是高中一线教师的“家常饭”，也成为教师提高教学水平的基本手段之一，只不过有时为了节省时间，在平时考试中，教师们往往从一些现有的模考题或高考题中直接选取或者稍作改变，并没有真正理解和体悟考题的价值和发挥其对课堂教学的导向作用.近期，南京市六校联合体组织了一次高三年级摸底考试，要求本次联合考试题必须为原创试题，笔者有幸成为命题组成员，被要求命制一道直线和圆的填空题，且该题在整个试卷的13题位置，属于中档难度试题，以下笔者分享和交流命制这道试题的历程及思考，欢迎批评指正.

一、原创试题

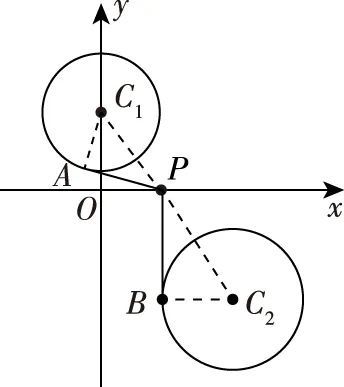
题目：平面直角坐标系xOy中，点P在x轴上，从点P向圆C1：x2+(y-3)2=5引切线，切线长为d1，从点P向圆C2：(x-5)2+(y+4)2=7引切线，切线长为d2，则d1+d2的最小值为________.

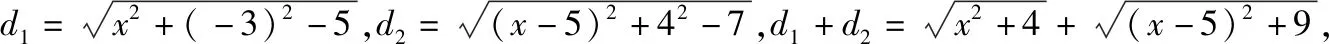
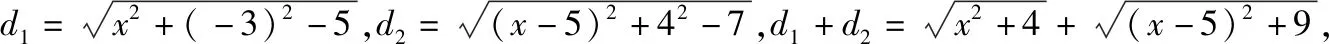
二、设计思路

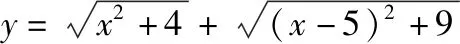
三、编题的过程

1.命题要求

题目内容：直线与圆的位置关系.

题目难度：中档题，难度和要求与高考考纲一致.

2.研读高考题

结合以上基本要求，为了更好地完成本次命题任务，保证命制的试题符合江苏高考试题模式，所以笔者认真学习了自2008年以来的江苏高考真题中所有有关距离的试题，以期从中找到灵感.

(1)研读考查直线和圆的位置关系的问题

对2008年以来的直线和圆的问题进行了梳理和归纳，其目的是把握命题的难度和方向以及寻找命题的灵感.笔者发现绝大多数直线和圆的问题都是借助圆的方程来研究圆或直线的性质，有时候利用几何性质可以简化运算.比如：

题目1(2010·江苏卷·9)在平面直角坐标系xOy中，已知圆x2+y2=4上有且仅有四个点到直线12x-5y+c=0的距离为1，则实数c的取值范围是________.

(2)研读考查非直线和圆的位置关系的问题

目的是迁移、发散思维，寻找命题的灵感.比如：

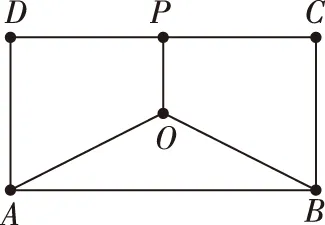
题目2(2008·江苏卷·17)如图，某地有三家工厂，分别位于矩形ABCD的两个顶点A，B及CD的中点P处，AB=20 km，BC=10 km.为了处理三家工厂的污水，现要在该矩形区域上(含边界)，且与A，B等距离的一点O处，建造一个污水处理厂，并铺设三条排污管道AO，BO，PO.记排污管道的总长度为ykm.

(Ⅰ)按下列要求建立函数关系：

(ⅰ)设∠BAO=θ(rad)，将y表示为θ的函数；

(ⅱ)设PO=x(km)，将y表示为x的函数.

(Ⅱ)请你选用(Ⅰ)中的一个函数关系，确定污水处理厂的位置，使铺设的排污管道的总长度最短.

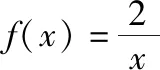
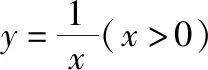
通过对江苏高考真题的研读，笔者发现，距离最短问题是江苏高考常考点，每年的高考试题中都会有所体现.而且，以直线和圆为背景的最值问题很好地考查了学生的理性思维、分类思想以及综合运用所学知识分析问题、解决问题的能力，倍受高考命题专家的青睐.

3.研读教材

根据多年的教学实践，笔者发现，经典的高考试题大多是从教材中题目演变而来的，教材中的习题可分为练习、习题、复习参考题、本章测试，不同题目的指向目标也不一样.因此，作为一线教师，应该多研究教材上的题目之间的联系，研究高考试题和教材中的习题之间的联系，认真思考，发现联系，对于原创试题很有指导意义.因此，笔者试图从教材苏教版《必修2》中“直线与圆的位置关系”一节的内容寻找命题的点.比如，苏教版《必修2》中“直线与圆的位置关系”一节后练习题第6题：从圆(x-1)2+(y-1)2=1外一点P(2，3)向圆引切线，求切线长.笔者从中得到启发.

通过以上两方面的研读、学习，切线长问题是自2008年以来高考尚未涉及的内容，容易成为学生学习的盲点，所以笔者试图以这方面知识为背景命制一道试题.

4.原创雏形

初稿：平面直角坐标系xOy中，从动点P向圆C：x2+(y-3)2=1引切线，切线长为d1，点P到x轴的距离为d2，则d1+d2的最小值为________.

基本想法：以直线和圆为背景，将切线长(距离)与其他距离进行组合命制试题，具体想考查二元变量最值问题的基本解决方法.但因为这个问题没有最小值，只能证明无限接近2，况且这类问题高考也从未涉及，所以考虑给动点加个限制条件，减少变量个数.

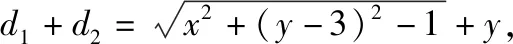
【评注】最值问题一般通过函数的单调性或者不等式求解，通过不等式求解的方法中很多都是和完全平方式联系在一起的，比如二次函数的顶点式，判别式法，基本不等式等等.本题虽可为教学中贯穿基本方法以及基本方法之间的联系提供资源，但设参数，将最值问题转化成方程的有解问题的解题思路，学生不常用，不易想到；一道好题还应该体现出学生的差异性，让不同的学生有不同的收获，因此，放弃了本稿.

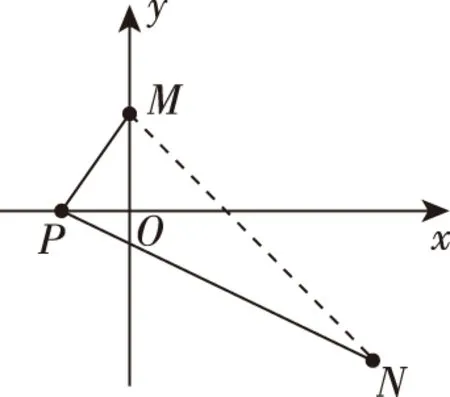
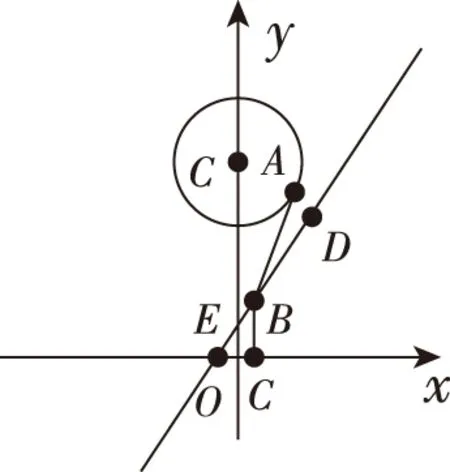
再稿2：平面直角坐标系xOy中，点P在x轴上，从点P向圆C1：x2+(y-2)2=1引切线，切线长为d1，从点P向圆C2：x2+(y+3)2=1引切线，切线长为d2，则|d1-d2|的最大值为________.

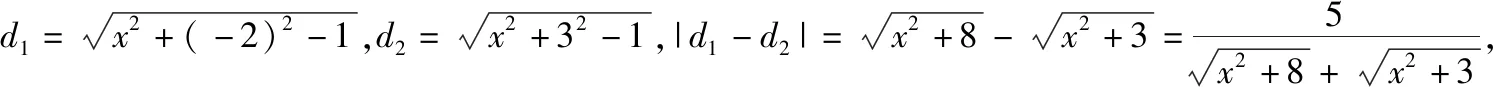
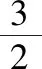
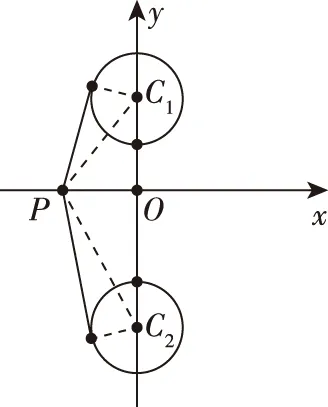
再稿3：平面直角坐标系xOy中，点P在x轴上，从点P向圆C1：x2+(y-2)2=1引切线，切线长为d1，从点P向圆C2：x2+(y+3)2=1引切线，切线长为d2，则d1+d2的最小值为________.

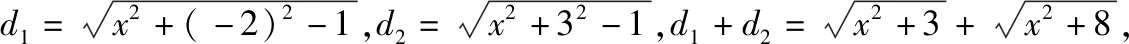
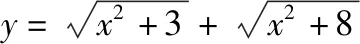
5.其他变式

变式1.平面直角坐标系xOy中，点P在x轴上，从点P向圆C1：(x+3)2+(y-2)2=3引切线，切线长为d1，从点P向圆C2：(x-3)2+(y+3)2=8引切线，切线长为d2，若d1+d2=10，求点P的坐标.

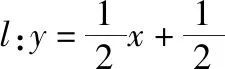
上述变式考虑的均是以圆的切线长为背景的问题，当然，我们还可以发散到以二次曲线的切线长为背景的问题，将直线上的动点，发散到曲线上的动点等，更期待各位同仁的参与.

四、试题测量与评价

考试结束后，笔者对学生的答题情况进行了全面的统计与分析，获得了试题的质量指标，试题难度为0.448，区分度为0.606.从学生答题情况看，44.8%的同学得5分，其余的同学得0分，对得0分的同学进行后期调访时发现：40.7%是因为没有时间去做造成的，43.5%是因为没有读懂题意导致没有解题思路造成的,15.8%是直接放弃.

总的来讲，本题的设计科学、严谨、新颖，具有一定的美感，符合高考的考纲要求，对学生具有一定的针对性，高考是选拔性考试，高考试题一定要有区分度，以利于不同层次学校对人才的选拔.作为测试卷填空题的小压轴题，本题起到了较好的把关作用，有效地区分了学生的数学思维能力和学科素养.

五、思考

从试题涉及的知识体系看，原创试题要关注数学知识体系的主干内容，在知识的交会处设计试题；从试题涉及的思想方法看，原创试题要关注试题的“可持续发展”功能，试题立意要明确，不能廉价转化、机械组合，也不要有意设置陷阱，同时，原创试题时也要特别关注语言表述，尽量做到简洁，避免歧义.原创试题的“新”更要体现在情景与方法的选择上，不要让技巧和繁琐的运算淡化了主题，当然，原创试题也有它的时效性，需要不断更新，再好的新题，学生做过几次后也就成了旧题.