基于CW方程的航天器追逃问题半直接求解方法

孙松涛，祝强军，宋 斌

(上海宇航系统工程研究所，上海 201109)

0 引言

两航天器追逃问题是一个双方对抗的控制策略问题。因航天器的动力学模型复杂,且双方的对策目标相反，故此追逃问题的求解十分困难。在航天器追逃过程中，追逐航天器期望选择使支付函数最小的控制策略，而逃逸航天器则期望选择使支付函数最大的控制策略，此追逃过程可由微分对策表述。微分对策最早由ISAACS[1]提出。随着研究的深入，BERKOVITZ等[2-3]给出了微分对策鞍点存在定理和最优控制策略存在的必要条件的严格推导。

虽然已知最优策略的必要条件，但针对此必要条件进行求解难度较大。此必要条件对应一个两点边值问题，该问题一般没有解析解，只能运用数值算法，而数值算法各有优缺点。目前，已有的数值方法包括配点法[4]和多重打靶法[5]。配点法将微分方程在配点处近似成代数方程，从而求解满足两点边值约束和代数方程约束的变量，进而求解两点边值问题。这种方法虽然收敛性好，但计算结果精度不高，计算过程中运算量大，且初值需要选择。多重打靶法通过数值积分公式在众多子区间上将一个微分方程离散成代数方程，在任意子区间上求解一个初值问题，通过不断优化每个区间上的初始值，最终满足两点边值条件。与配点法相比，多重打靶法计算速度快，计算精度较高，但对初值非常敏感，因此收敛性差。航天器追逃问题多对应复杂的动力学模型。由配点法和多重打靶法的表述可知，这2种方法的收敛性都与初值选择有关，配点法虽对边值问题收敛性较强，但因航天器追逃模型为较复杂的非线性模型，若随机给出初值问题，则仍然不收敛。

本文为求解航天器追逃问题提供了一种新思路。采用半直接配点法求解此问题，避免了对两点边值问题的求解。研究思路来源于HORIE等[6-7]对导弹拦截问题的研究。该方法通过变换将微分对策问题转化成最优控制问题。将最优控制问题构造成一个非线性规划问题后，可运用序列二次规划(SQP)算法进行求解。但HORIE等提出的方法并不能说明半直接配点法求解微分对策问题与原问题的等价性。本文在文献[8]中证明了半直接配点法求解微分对策问题的等价性，为半直接配点法求解微分对策问题提供了理论依据。在求解两航天器追逃问题的过程中，通过半直接变化将微分对策问题转化成最优控制问题，采用Guass-Lobbato配点法对此问题进行数值求解，可提高数值方法的收敛性和稳定性。

本研究在地点为近地轨道附近，对抗双方均为连续小推力，对策时间较短，且瞬时状态信息完全已知的假设条件下，针对时间固定的追逃问题，以距离为支付建立对策模型，给出半直接配点法求解此追逃问题的数值方法。最终给出追逃双方在对策条件下的最优策略和仿真算例，为航天器追逃问题提供了一种有效的求解方法。

1 航天器追逃问题

针对两航天器轨道追逃问题，建立动力学方程，以描述追逐航天器P与逃逸航天器E在追逃过程中的运动规律，即

(1)

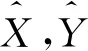
两航天器的位置关系如图1所示。

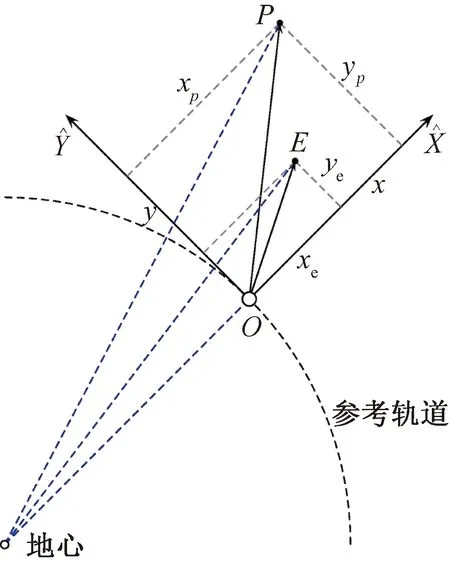
图1 两航天器对策的坐标示意图Fig.1 Coordinate schematic diagram of pursuer and evader

在式(1)中，追逐航天器P和逃逸航天器E的控制量满足约束条件

式中：‖·‖2为欧氏范数。

此航天器追逃问题的支付函数为

式中：

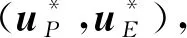
为说明上述航天器追逃问题的一般求解方法，下节将给出此追逃问题最优策略存在的必要条件。

2 最优策略存在的必要条件

在一般的微分对策数值求解中，针对最优策略必要条件的求解是解决微分对策问题的关键。

(2)

根据微分对策原理[3]，将Hamilton方程H定义为

H=HP+HE

(3)

式中：

为给出此追逃问题最优控制策略的必要条件，令

λP=[λ1Pλ2Pλ3Pλ4Pλ5Pλ6P]T

λE=[λ1Eλ2Eλ3Eλ4Eλ5Eλ6E]T

其中，λP和λE分别为协态向量，则式(3)可表示为

根据最优策略存在的必要条件[2]，协态方程为

(4)

(5)

式(4)，(5)相应的边值条件为

(6)

(7)

(8)

显然，最优策略的必要条件式(2)，(4)，(5)，(6)，(7)组成了一个两点边值问题，一般的两点边值问题可由多重打靶法求解[8]。

3 半直接配点法

在半直接配点法中，将由最优策略必要条件得到的追逐或逃逸航天器的协态变量加入到状态方程中，同时将对应航天器的最优控制量表达式代入对应的状态方程并加入约束条件，进而将微分对策问题转化为最优控制问题。在求解时，只需求解对应的支付函数最大或最小问题即可。相应的等价性证明参考文献[8]。

3.1 半直接转换

半直接配点法将微分对策问题转化为最优控制问题，这里将逃逸航天器对应的协态变量加入到微分方程中(对应的追逐航天器的半直接转化过程同理)，变换的方法简述如下，令

(9)

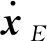
由于协态变量λE加入到式(9)中，相应的终端约束方程Ψ定义为

则变换后的支付函数为

显然，微分对策问题已被转化为最优控制问题。接下来，将给出基于配点法求解转化后最优问题的方法。

3.2 半直接配点法的数值求解方法

这里考虑计算的准确性[9]，将采用五阶Gauss-Lobbato配点法求解上述最优问题。为说明此方法，不妨设式(9)对应的微分方程为

(10)

根据配点法，在[ti，ti+1]区间上，需应用多项式近似式。由Gauss-Lobbato配点法[9]可知，除端点ti，ti+1外，其余3个配点tc1，tcm和tc2分别为

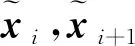
式中：Δti=ti+1-ti。

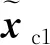
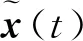
(11)

(12)

将式(11)，(12)相加可得

49fc2+9fi+1)

(13)

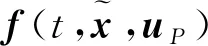
i=1,2,…,N

(14)

i=1,2,…,N

(15)

式中：N为区间数。

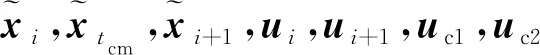
4 数值仿真结果

为说明半直接配点法求解的特点，将给出不同的仿真实例。因空间站和大量的卫星存在于地球低轨道，故在仿真中，将原点轨道高度分别设为500 km和1 000 km，并选择仿真时间均为500 s。对于同样的仿真实例，采用基于必要条件的数值方法(如多重打靶法)进行求解，若迭代初值不准确，则很难得到收敛的解。

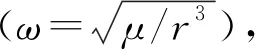
2个实例中，追逐航天器与逃逸航天器的初值见表1，两航天器的单位质量加速度见表2，其中，g=9.8×10-3km/s2。

表1 相对坐标系下的初值

表2 两航天器的单位质量加速度

为兼顾计算速度和计算准确性，选取10个子区间进行仿真。由子区间的选择可知，需要求解的变量为293个。在数值仿真计算中，运用Gauss-Lobatto配点法，将微分方程代数化后用SNOPT求解器进行求解[10]。在仿真中，选用处理器型号为Xeon E3-1230V2，内存为8 GB的台式机进行数值计算。设约束精度和优化允许误差均为10-9。

在实例2(原点轨道高度为1 000 km)中，两航天器轨迹和最优控制变量的变化曲线如图3所示。

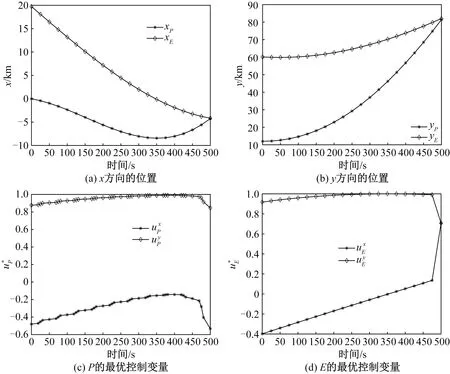
图2 实例1：追逐和逃逸航天器的轨迹和最优控制变量Fig.2 Test case 1: trajectories and optimal control variables of pursuer and evader

图3 实例2：追逐和逃逸航天器的轨迹和最优控制变量Fig.3 Test case 2: trajectories and optimal control variables of pursuer and evader

在图3中，各子图的表示方法同图2。由图3可知：追逐航天器可追上逃逸航天器。在仿真实例2中，根据数值计算结果可知：约束误差为2.551 2×10-10，计算时间为17.58 s。

由图2可知：在500 s的规定时间内，追逐航天器对逃逸航天器进行了成功拦截，追逐者和逃逸者的控制变量变化规律相似，两者采用了近似的追逃策略。由图3可知：追逐者和逃逸者的对策时间为500 s，在500 s内，追逐航天器对逃逸航天器进行了成功拦截。

5 结论

本文采用半直接配点法求解了近地轨道的追逃问题，得到了收敛的解，半直接配点法将一个微分对策问题转化成了一个最优控制问题，运用Gauss-Lobbato五阶配点法，并结合序列二次规划法，最终解决了一个非线性的数学规划问题。半直接配点法求解微分对策问题时，可避免求解困难的两点边值问题。该算法具有收敛性好、应用简单的特点。数值仿真实例验证了这种求解方法的可行性。该方法提高了求解两点边值问题的收敛性，为求解含有双方控制变量的微分对策问题提供了一种思路。