基于不同动力引力辅助模型的木星转移轨道设计

杨 彬，杨洪伟，李 爽，尤 伟

(1. 南京航空航天大学 航天学院，江苏 南京 210016； 2. 南京航空航天大学 航天新技术实验室，江苏 南京 210016； 3. 上海卫星工程研究所，上海 201109)

0 引言

随着空间技术的快速发展，我国的深空探测能力逐渐提高。以木星为代表的外太阳系天体成为我国下一步深空探测的目标[1]。对于这类距离地球遥远的目标，传统的直接转移方式因燃料消耗巨大而不再适用。引力辅助技术作为重要的节能技术，对于深空探测轨道设计具有重要意义。引力辅助技术的应用能有效减少任务的燃料消耗，使得原本无法完成的任务成为可能。而且，除了完成对既定目标的探测外，探测器在行星引力辅助过程中还能完成对引力辅助行星的飞越探测，增加任务的科学回报。国外包括旅行者号[2]、卡西尼号[3]在内的一系列深空探测器均采用了引力辅助技术，极大减少了任务的燃料消耗。

引力辅助技术，即在探测器靠近某一星球时，借助该星球的引力作用来改变探测器的轨道与速度，是一种无消耗的轨道机动方式。引力辅助技术的应用使得深空探测轨道设计变得更加复杂多样。为获得较好的引力辅助效果，针对复杂引力辅助轨迹的优化设计一直是轨道动力学的热点话题。CESARONE[4]推导了引力辅助过程中的参数表达式，并分析了近心点高度等引力辅助参数对引力辅助轨迹的影响。尽管引力辅助技术在节省燃料、提高效率等方面具有显著优势，但其对所涉及天体的相位关系要求十分严格，借力前后的速度必须严格匹配[5]。这使得引力辅助转移轨迹的发射窗口变得十分狭窄，造成搜索过程收敛困难。为提高发射窗口搜索算法的稳定性，LONGUSKI等[6]提出了特征能量C3匹配法，基于引力辅助前后探测器的特征能量进行引力辅助转移轨迹匹配。张旭辉等[7]采用蒂塞朗准则对C3匹配方法进行了验证。乔栋等[8]提出了软匹配策略，用以进行轨道拼接。软匹配策略的应用有效解决了传统方法对满足约束条件转移轨道方案的遗漏问题。虽然采用了各种方法来提高匹配的稳定性，但等待相关行星到达理想相位关系，往往需要数年时间。而且，针对多天体引力辅助情况，等待时间将更长。

为弱化引力辅助技术对能量匹配的约束，一些学者提出在引力辅助过程中，通过施加主动脉冲来改善引力辅助效果，增加任务窗口，减少相位等待时间。PRADO[9]对带有脉冲机动的引力辅助变轨进行了描述，并推导了探测器速度、能量变化量等参数，给出了特定条件下的最优脉冲机动方向。引力辅助过程中脉冲施加的具体位置目前仍是轨道动力学研究的热点问题[10-12]。李小玉等[13]研究了附加深空机动的引力辅助模型，推导了引力辅助后离开剩余速度的解析表达式。贾建华等[14]分析了平面引力辅助过程中施加脉冲的最优位置，给出了平面情况下的最优脉冲施加位置确定方法。CASALINO等[15]研究了在近拱点施加脉冲机动的引力辅助，但其所提方法只适用于脉冲幅值较小的情况。贾建华等[16]分析了三维情况下近拱点施加脉冲的大小和方向对探测器轨道的影响。除了在近拱点施加脉冲机动外，另一种方案是在引力辅助完成后施加脉冲机动。侯艳伟等[17]采用这种方式设计了基于金星引力辅助的火星转移轨道。

本文针对有动力引力辅助技术和木星探测转移轨迹进行了研究，主要对近心点脉冲机动和甩摆后脉冲机动2种引力辅助模型进行了对比分析，并完成了木星引力辅助转移轨迹的初始设计。首先，分别构建近心点机动引力辅助模型和甩摆后机动引力辅助模型。然后，提出基于引力辅助模型进行深空探测的转移轨道设计方法。随后，以木星探测任务为工程应用背景，基于不同引力辅助行星方案测试2种动力引力辅助模型的性能。数值仿真结果表明：近心点施加脉冲机动的引力辅助方案具有更好的节能效果。最后，应用近心点机动引力辅助模型，采用地球-金星-金星引力辅助序列，完成木星探测任务转移轨迹的设计。

1 动力引力辅助模型

引力辅助作为一种高效的节能技术，多次为深空探测任务所采用。但对于轨道设计而言，包含引力辅助的转移轨迹颇为复杂。因此，各种简化模型被采用，以在保证一定精度的前提下尽量提高计算效率。其中，圆锥曲线拼接法所采用的影响球模型是目前初始设计最常用的简化模型。根据圆锥曲线拼接法的原理，引力辅助过程被假设为一个瞬时速度突变。其中，速度突变量的大小根据影响球模型估算求解。无动力引力辅助方式受到安全飞越高度等因素限制，在大多数情况下不能满足任务要求。因此，在引力辅助过程中或引力辅助结束后通过施加脉冲机动来匹配引力辅助前后的转移轨迹是一种有效方式。这种将主动变轨和引力辅助相结合的方式被称为有动力引力辅助技术。本文将针对近心点机动和引力辅助后机动2种动力引力辅助方式进行建模分析。

1.1 近心点机动引力辅助模型

近心点机动引力辅助过程中只考虑引力辅助行星的引力作用，即探测器进入借力行星影响球后沿双曲线轨道接近借力行星。当其飞至近心点时，沿速度方向施加脉冲机动，以修正探测器引力辅助完成后的状态。随后，探测器沿调整后的逃逸轨道飞出借力行星的影响球，完成引力辅助。

相比于漫长的星际转移过程，引力辅助过程持续时间很短。因此，假设引力辅助瞬时完成，则引力辅助前后探测器的位置不变且与引力辅助行星位置重合。探测器引力辅助前后的速度v+和v-分别通过求解引力辅助前后2段转移轨迹的Lambert问题得到。因此，探测器进入借力行星影响球的剩余速度和理想的离开剩余速度分别为

(1)

式中：vP为借力行星在引力辅助时刻的速度。若探测器以理想剩余速度进入和离开引力辅助行星的影响球，则进入和离开影响球的真近点角等于双曲线轨道渐近线的真近点角。进入和离开的真近点角的数学表达式分别为

(2)

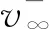
根据双曲线的性质，进入和离开真近点角和双曲线剩余速度偏转角δ满足几何约束，f+-f--δ-π=0。将式(2)带入几何约束方程，得到关于近心点高度的非线性方程

(3)

为求解非线性方程(3)，对其求一阶导数和二阶导数，即

(4)

(5)

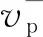
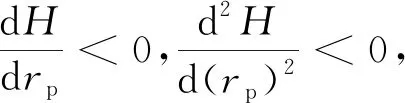
(6)

1.2 甩摆后机动引力辅助模型

动力引力辅助除在近心点添加机动外，另一种常见的方案是在引力辅助完成后立即施加速度脉冲进行调整，使得探测器的状态满足后续飞行任务的要求。施加的速度增量满足

v+=v-+ΔvGA+ΔvI

(7)

式中：ΔvGA为引力辅助行星提供的速度增量；ΔvI为引力辅助完成后探测器施加的速度增量。在式(7)中，当任务时间确定后，引力辅助前后探测器的速度是固定的。因此，为节省燃料，只能调节引力辅助提供的速度增量，使得探测器提供的速度增量最小。

为方便描述，本文采用引力辅助坐标系[12]描述引力辅助过程的参数，如图1所示。

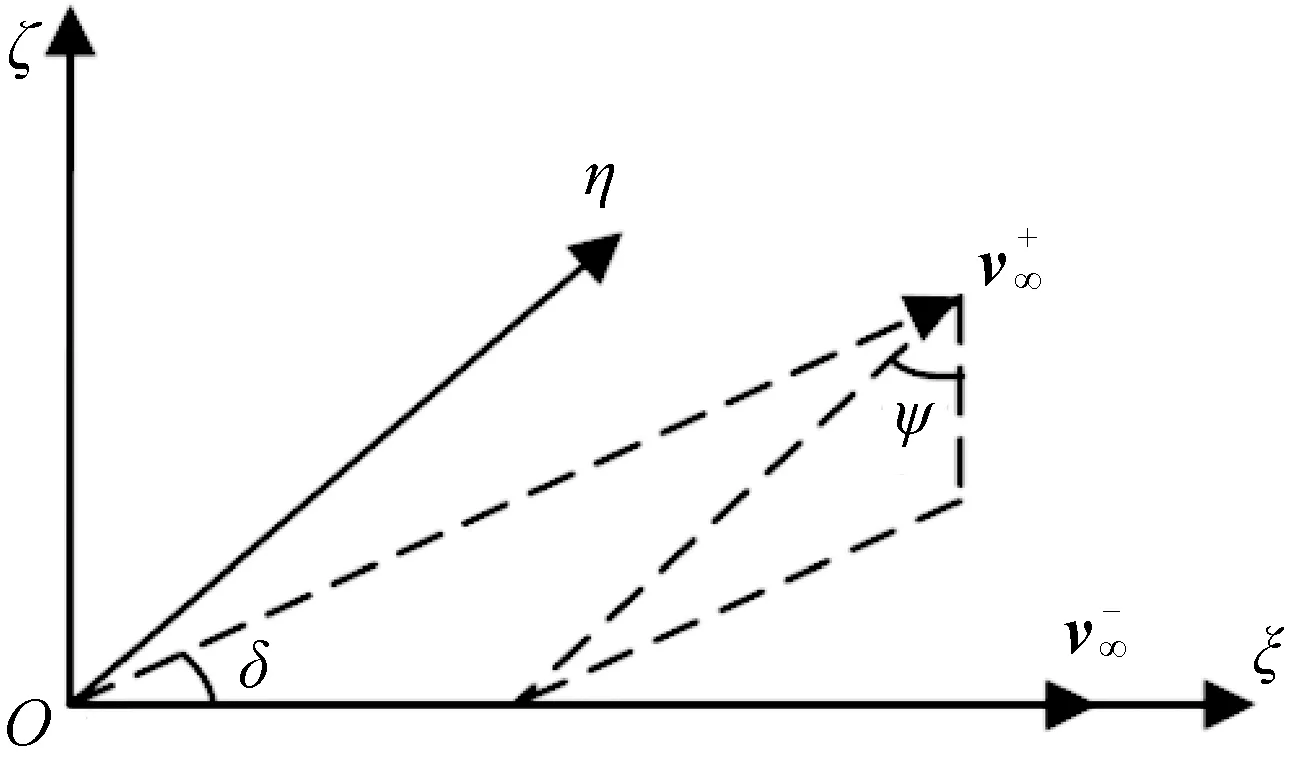
图1 引力辅助坐标系Fig.1 Gravity assist reference frame

图中：坐标原点O位于引力辅助行星的中心，ξ轴沿双曲线进入剩余速度方向，ζ轴垂直于引力辅助前探测器的速度与引力辅助行星速度所决定的平面，η轴与ζ轴和ξ轴构成右手坐标系。将坐标轴方向的单位矢量分别记为i，j和k，用剩余速度矢量和行星状态表示，如式(8)所示，具体推导过程详见文献[12]，此处不再赘述。

(8)

在引力辅助坐标系中，探测器进入和离开双曲线剩余速度表示为

(9)

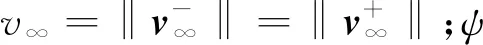
(10)

在引力辅助坐标系中，引力辅助行星提供的速度增量可表示为

(sinδsinψ)j+(cosδ-1)i]

(11)

此外，将引力辅助前后的速度差投影至引力辅助坐标系，即

v+-v-=v∞(κ1i+κ2j+κ3k)

(12)

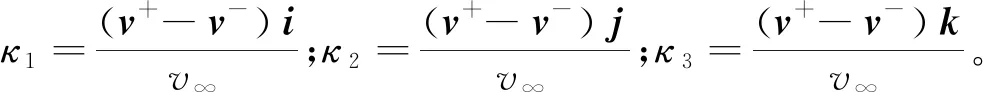
将式(11)，(12)带入式(7)，可得

ΔvI=v∞[(κ1-cosδ+1)2+(κ2-sinδsinψ)2+

(13)

因此，只要确定剩余速度偏转角δ和甩摆角度参数ψ，就能求得引力辅助完成后所需施加的脉冲机动速度增量。

2 转移轨迹设计

转移轨迹设计是空间任务规划的基础。圆锥曲线拼接法是经典的转移轨迹初始设计方法。采用该方法能快速完成转移轨迹初始设计。本文基于上述引力辅助简化模型，采用圆锥曲线拼接法进行复杂的引力辅助转移轨迹设计。嵌入引力辅助简化模型的圆锥曲线拼接法的执行过程如图2所示。

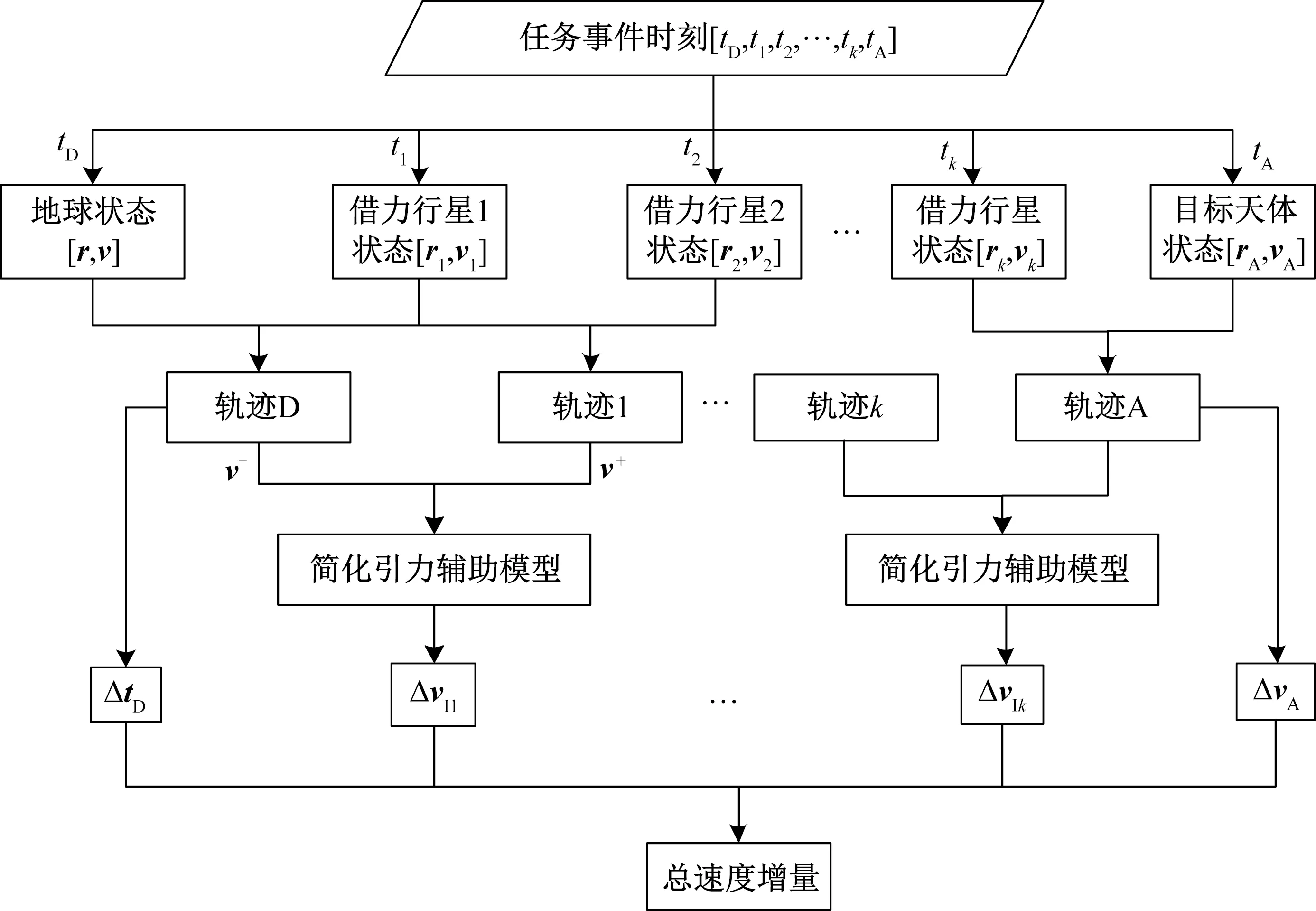
图2 嵌入动力引力辅助模型的圆锥曲线拼接法流程图Fig.2 Flowchart of patched conic method with powered gravity-assist model

首先，在已知探测器地球出发时刻、行星借力时刻和目标到达时刻的条件下，通过星历可求得相关天体在相应时刻的状态。然后，基于圆锥曲线拼接法的思想，求解Lambert问题，得到相邻天体之间的转移轨迹，如图2中所示的轨迹D和轨迹1。最后，利用引力辅助模型将这些转移轨迹段按顺序拼接，并计算引力辅助过程中所需施加的脉冲速度增量，进而得到任务所需的总速度增量。

因此，转移轨迹设计问题被转化为一个多变量优化问题，即通过挑选最优的任务时间节点和引力辅助参数(近心点高度、甩摆角度等)，使整个任务的燃料消耗最少。对于这种多变量全局优化问题，遗传算法具有明显优势。所以，本文后续的轨道设计将采用遗传算法进行优化，其性能指标为探测器提供的总速度增量。

3 仿真试验与结果分析

3.1 引力辅助方式比较

以基于单次引力辅助的木星探测任务为例，对比分析2种简化引力辅助方案。为方便对比，除引力辅助模型外，其他任务条件完全一致。探测器于2032年11月8日从地球出发，于2033年4月27日完成金星引力辅助后飞往木星，并最终于2036年9月1日抵达木星。根据第2节描述的转移轨迹设计方法，分别带入近心点机动引力辅助模型和甩摆后机动引力辅助模型，计算最终的速度增量。仿真结果见表1。

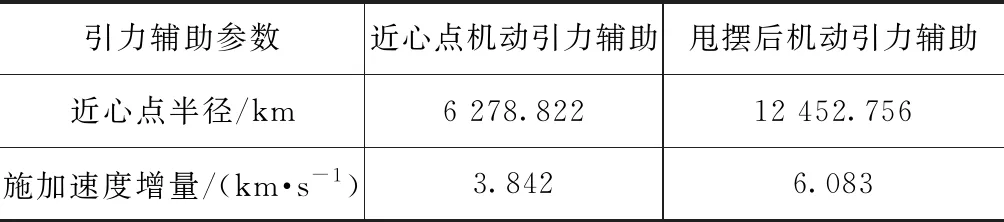
表 1 不同地球引力辅助方案的对比

由表可知：金星引力辅助过程中，近心点机动所需的速度增量要远远小于甩摆后机动所需的速度增量，且前者在引力辅助过程中的近心点半径也较小。这表明：在引力辅助过程中，探测器能从金星获取更多能量，从而减小自身所需提供的速度增量。由此可见：相比于甩摆后的机动方案，近心点机动方案能节省更多能量。为验证这一结论，针对地球和火星引力辅助任务进行仿真，结果见表2。

表 2 不同情况下的引力辅助模型对比

相比于表1，表2中引力辅助过程中需要施加的速度增量大大减小，且不同动力引力辅助方案的近心点半径差异并不明显。但是，相对于甩摆后机动的引力辅助方案，近心点机动方式的燃料消耗仍然较小，只是其优势并没有表1中那么明显。综上所述，近心点机动的引力辅助方式能使探测器以更少的燃料消耗完成引力辅助前后的轨迹拼接。因此，后续木星探测任务转移轨迹的设计将采用近心点机动引力辅助模型。

3.2 木星转移轨迹设计

木星是太阳系最大的行星，对于研究太阳系的起源具有重要意义。迄今为止，包括NASA，ESA在内的多家航天机构已发射了伽利略号、朱诺号等木星探测器。此外，木星探测也已纳入了我国未来的深空探测规划。

木星距离地球十分遥远，现有探测器均采用行星引力辅助技术转移至木星，且为进一步节省燃料，往往在抵达木星前实施多次行星引力辅助。金星-地球-地球引力辅助序列是常见的木星探测任务方案之一。本文将基于此序列完成木星转移轨迹的初始设计。结合我国的木星探测计划，将发射窗口搜索区间设定为2030年1月1日至2036年12月31日。性能指标为探测器提供的总速度增量，即

J=Δvtotal=‖ΔvD‖+‖ΔvA‖+

∑‖ΔvGAk‖

(14)

式中：ΔvD为探测器离开地球所需的速度增量；ΔvGAk为第k次引力辅助所需施加的速度增量，其值可通过1.1节中所述模型求解；ΔvA为探测器到达木星后完成木星捕获所需的速度增量。考虑到木星高强度的辐射，将木星目标捕获轨道的近木点半径设定为不得小于4倍的木星半径。另外，为减小木星捕获所需的速度增量，将捕获轨道的远木点半径设定为100倍的木星半径。因此，探测器的目标捕获轨道为100RJ×4RJ的大椭圆环木轨道。木星捕获所需的速度增量为

(15)

式中：vA∞为探测器到达木星时的剩余速度；μJ为木星引力常数；ra和rp分别为目标捕获轨道的近木点半径和远木点半径。

为确保探测器在引力辅助过程中的安全，对不同引力辅助行星的引力辅助轨迹的近心点半径添加必要的约束，约束条件见表3。

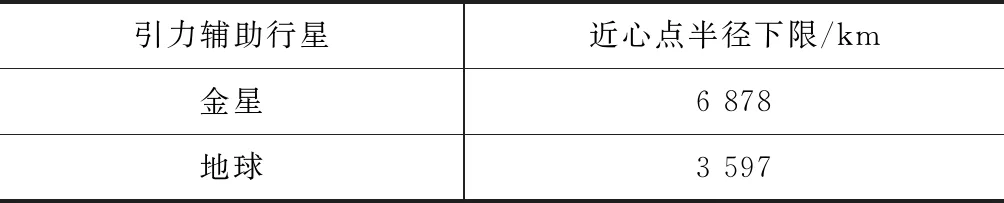
表3 不同行星引力辅助近心点半径下限

采用遗传算法进行寻优，其进化过程如图3所示。经过25代遗传搜索的最优速度增量为1.170 km/s，最优解的详细信息见表4。

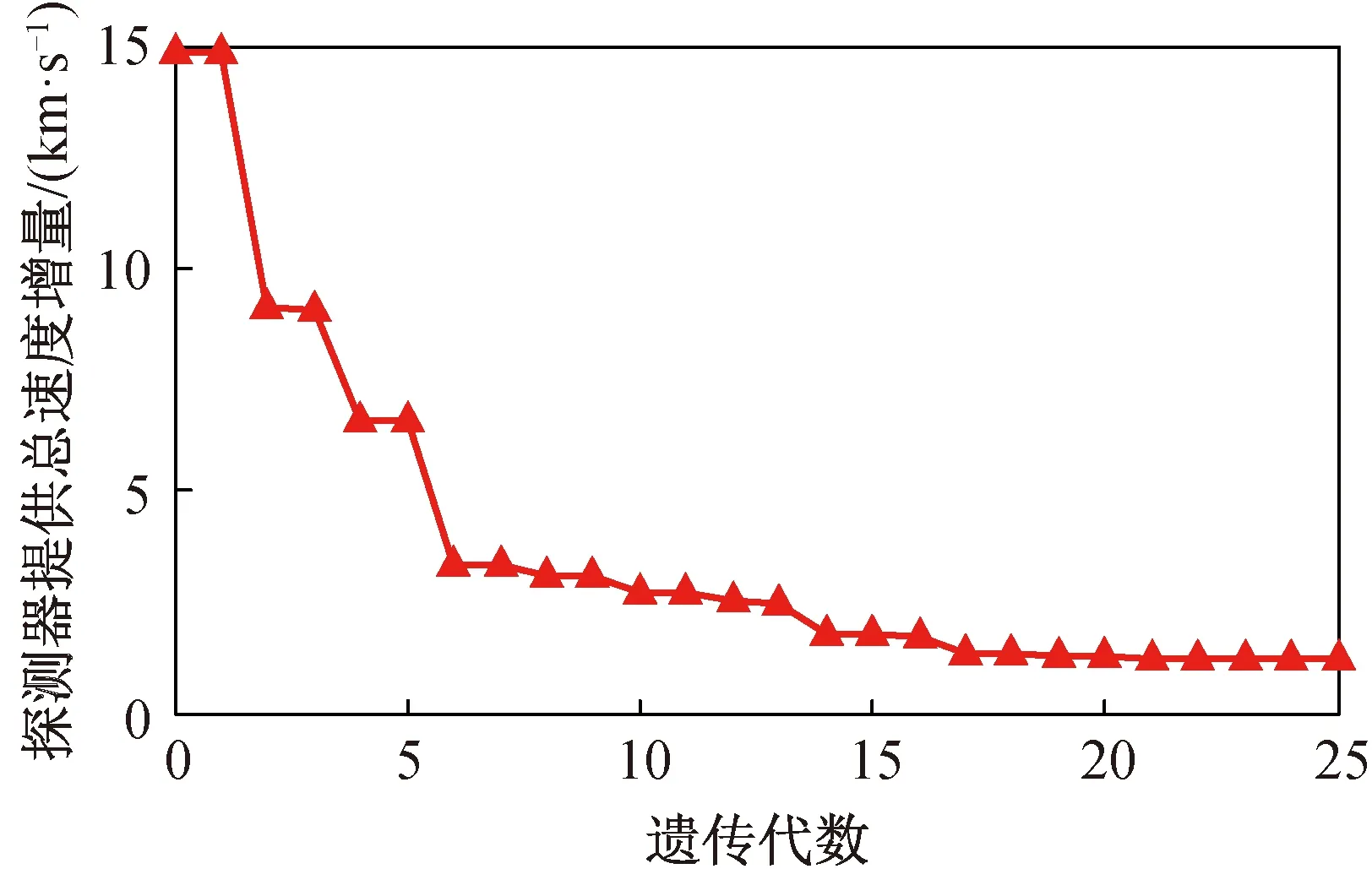
图3 遗传算法搜索进化图Fig.3 Search process of genetic algorithm

探测器于2033年1月11日从地球发射，经过159 d的星际转移，于2033年7月3日到达金星，完成金星引力辅助后返回地球。2034年6月2日，探测器首次返回地球，完成第一次地球引力辅助。探测器于334 d后再次返回地球，在完成第二次地球引力辅助后，进入前往木星的转移轨道，并于2039年6月12日到达木星。整个转移过程持续2 343 d，需要探测器提供的总速度增量为1.17 km/s。任务转移轨迹如图4所示。

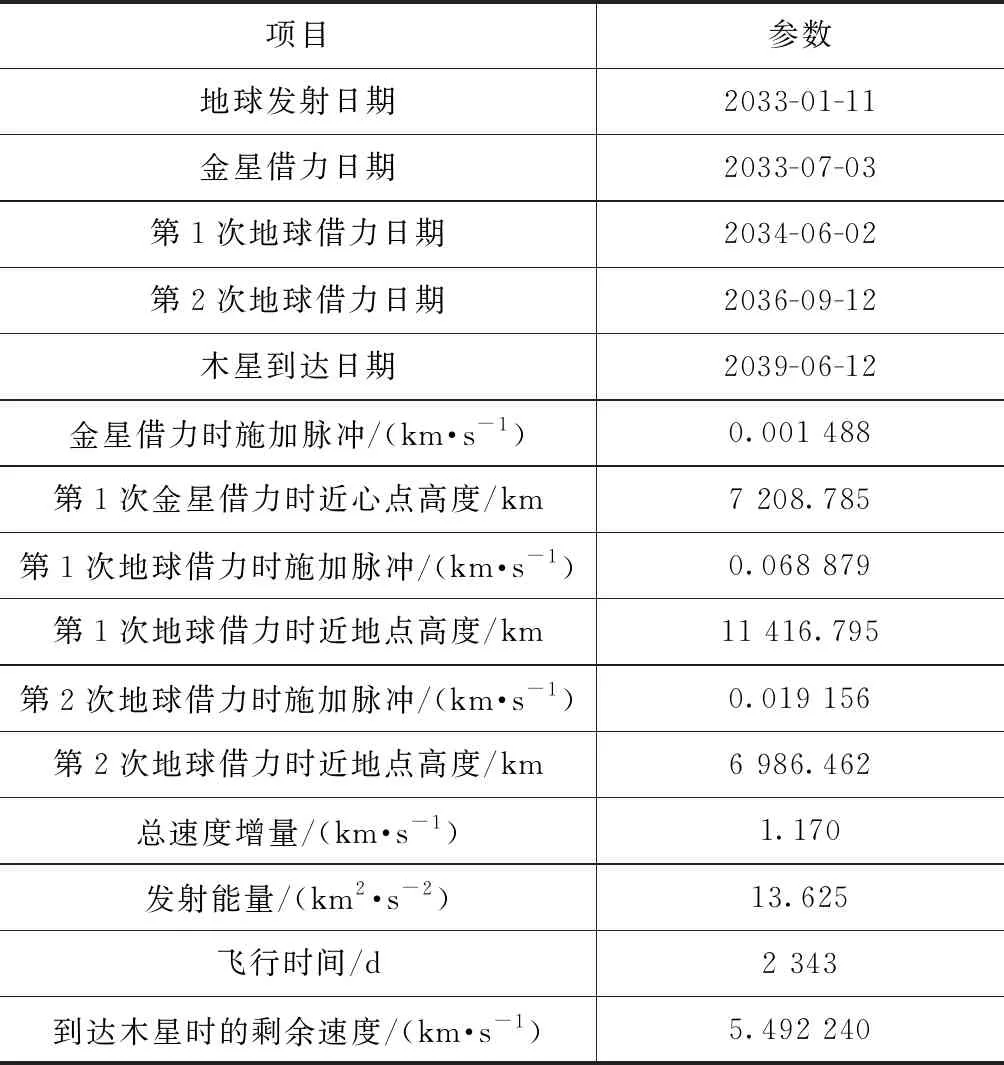
表4 遗传算法搜索结果详细信息表

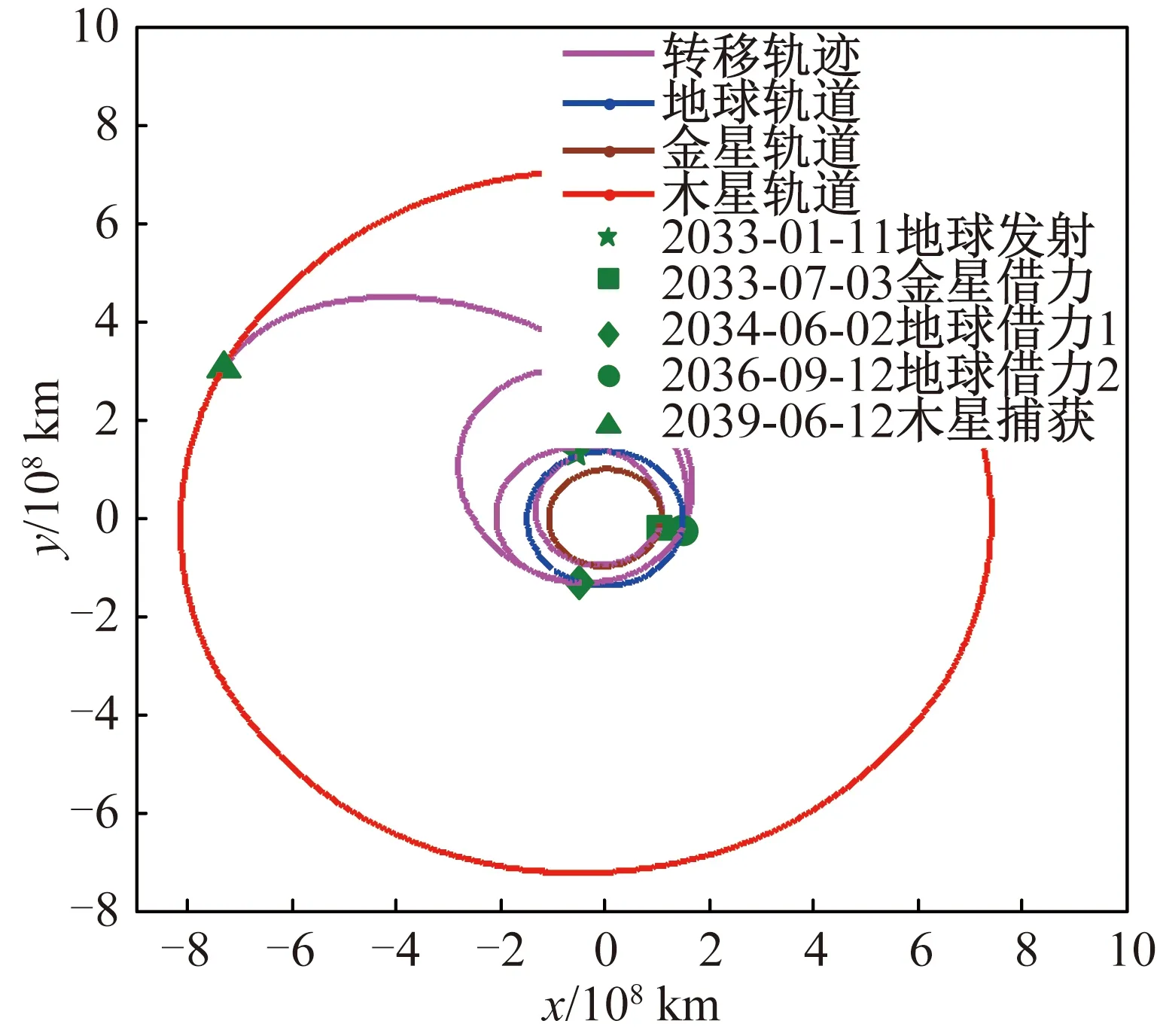
图4 木星探测转移轨迹示意图Fig.4 Transfer trajectory for Jupiter mission

4 结论

本文对比分析了近心点机动和甩摆后机动2种引力辅助方式。仿真结果表明：采用行星引力辅助时，在近心点施加脉冲机动比引力辅助完成后施加机动更加节能。基于此结论，本文完成了木星多天体引力辅助转移轨迹的初始设计，其中包含1次金星引力辅助和2次地球引力辅助。本文研究内容和结论对我国后续木星探测等深空探测任务具有一定的参考意义。但是，本文提出的模型只适用于脉冲机动方式。随着电推进等连续小推力推进技术的成熟和在工程中的应用，针对小推力和引力辅助相结合的轨道设计与优化将是未来轨道设计的热点。因此，后续将针对小推力引力辅助技术进行深入研究。