关注两个数列恒等式模型的解题功能

黄旭明

(福建省福安市第三中学 355002)

2017年版高中数学课程标准，提出了高中数学学科核心素养的六个要素，数学建模是其中之一.数学建模是数学应用的重要形式，是解决问题的基本的手段，也是推动数学发展的动力.在等差数列、等比数列的学习中，结合它们的定义，再将通项公式an=a1+(n-1)d,an=a1qn-1变形、引申，不难发现两个更为一般的数学模型——差式恒等式和商式恒等式：

①an=a1+(a2-a1)+(a3-a2)+…+(an-an-1);

这两个恒等式看似平常，其实在解答数列问题中有着广泛的应用.

一、求数列的通项公式

例1 (见人教版课标教科书必修5 P35)已知a1=1,an=2an-1+1(n>1),求通项an.

解将an+1=2an+1与an=2an-1+1相减，得an+1-an=2(an-an-1)(n>1).

可见新数列{an-an-1}是公比为2的等比数列，它的首项是a2-a1=(2a1+1)-1=2,因此an-an-1=2×2n-2=2n-1(n>1).

根据差式恒等式①有

an=a1+(a2-a1)+(a3-a2)+…+(an-an-1)

类似地，可解答2014年高考题：设a1=1,an+1=3an+1,求an.

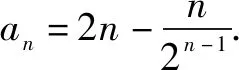
解将已知式分解因式，有

(an+1+an)[(n+1)an+1-nan]=0.

由an>0知an+1+an≠0,

由商式恒等式②有

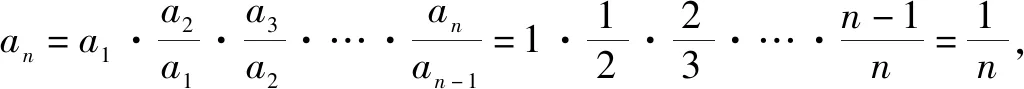
二、证明有关正整数的恒等式

有关正整数n的恒等式，通常习惯用数学归纳法来证明.实际上数学归纳法并不是唯一的方法，也不一定是最佳的方法，甚至有时无能为力.而这类题用两个恒等式来证明，有时会更为方便.

例4 (见人教版课标选修2-2 P94例1)求证：

两式相减，可得Sn-Sn-1=n2.由差式恒等式有

Sn=S1+(S2-S1)+(S3-S2)+…+(Sn-Sn-1)

=1+22+32+…+n2,

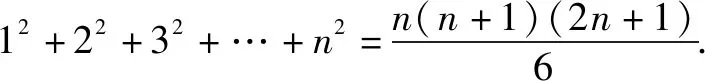
例5 求证(n+1)(n+2)(n+3)…+(n+n)=2n·1·3·5·…·(2n-1).

证明当n=1时，显然式子成立.当n≥2时，

记an=(n+1)(n+2)(n+3)+…+(n+n),则

an-1=n(n+1)(n+2)…(2n-2).

=2·(2×3)·(2×5)·…·[2×(2n-1)]

=2n·1·3·5·…·(2n-1),

所以(n+1)(n+2)(n+3)…(n+n)=2n·1·3·5·…·(2n-1).

三、证明有关正整数的不等式

对于a1+a2+…+an>(<)f(n)型的不等式，可记Sn=f(n),求出Sn-Sn-1的表达式，并与左端的对应项an比较，适当放缩，建立起Sn-Sn-1与an的不等关系，再用差式恒等式进行证明.对于a1a2a3…an>(<)g(n)型的不等式，类似地处理.

例6 (见人教版课标选修4-5P53习题3)求证：

所以Sn=S1+(S2-S1)+(S3-S2)+…+(Sn-Sn-1)

例7 (见人教版课标选修4-5P50下)求证n2<2n(n≥5).

证明记an=n2,则an-1=(n-1)2,

认识数学模型在解决问题中的作用，学会建立数学模型，这是发现问题，提出问题，分析问题，解决问题的重要手段.这不仅是数学知识的应用，更是数学思想、方法、价值所在，对学生数学核心素养的发展也起着支撑作用.