基于EMD和Hilbert包络谱分析的滚动轴承故障诊断研究

重庆交通大学 机电与车辆工程学院 重庆 400074

1 研究背景

滚动轴承是旋转机械中的重要零部件,也是最容易损坏的零部件。滚动轴承发生故障,将会对设备造成非常大的影响。因此,对滚动轴承的故障诊断技术进行研究,有十分重要的意义[1-2]。滚动轴承故障常用的诊断方法有经验模态分解(EMD)方法、短时傅里叶法、小波分析法等[3-4]。Norden E Huang等人在1998年提出对非平稳信号进行EMD,将其分成一系列本征模态函数(IMF),随后再通过Hilbert变换获取整个信号频谱[5]。张志刚等[6]提出一种改进的EMD方法,对信号的前期处理进行优化,但有较大的局限性。喻洋洋等[7]提出应用LabVIEW软件建立滚动轴承故障诊断系统,但缺乏必要的试验验证。孟宗等[8]提出基于压缩感知的方法来提取故障信息,但对硬件的采集及传输等方面要求较高,实现条件较为复杂。郝高岩等[9]提出一种改进阶次包络谱分析方法,这一方法对获取的信号进行包络分析后,再对信号进行滤波处理,能够较好地提取故障信息,但所需要的计算量较大,有较大的局限性。

上述方法都存在较大的局限性。为实现滚动轴承故障的检测与诊断,笔者针对滚动轴承的振动信号采用EMD方法,得到滚动轴承的IMF分量,再对这些IMF分量进行Hilbert包络解调分析,由此得到滚动轴承的故障特征信息,实现滚动轴承的故障诊断。

2 EMD概述

EMD方法本质是对信号的平稳化处理,尤其适用于非线性、非平稳信号的处理。这一方法可以将复杂非线性信号分解为有限个IMF分量[10],每个IMF分量必须满足两个条件[11]:一是在整个信号时域内的极点数与零点数相等,或者最多相差1;二是在信号上任意取一点,局部最大值所确定的包络线与局部最小值可确定的包络线均值为0。

对任何信号进行EMD时,对原始信号x(t)上的所有极大值点和极小值点分别采用三次样条函数进行拟合,所得到的两个函数拟合曲线作为原始信号x(t)的上下包络线。计算出它们的平均值,记为m1(t)。将原始信号x(t)与m1(t)相减,得到新的信号,记为h1(t):

h1(t)=x(t)-m1(t)

(1)

如果信号h1(t)不满足IMF的两个条件,那么需要将h1(t)作为原始信号重复上述步骤,筛选k次,直到信号h1k(t)满足IMF分量的两个条件,信号h1k(t)变为第一个IMF分量:

h1k(t)=h1(k-1)(t)-m1k(t)

(2)

式中:h1(k-1)(t)为筛选k-1次后的信号;m1k(t)为筛选k次后的上下包络线函数平均值。

由原始信号中分解得到一阶IMF分量,记为c1(t):

c1(t)=h1k(t)

(3)

从原始信号x(t)中减去c1(t),得到第一阶剩余信号,记为r1(t):

r1(t)=x(t)-c1(t)

(4)

再将r1(t)作为原始信号,重新按照式(1)～式(3)计算,得到第二个IMF分量c2(t)。

重复以上步骤,可以得到c3(t)、c4(t)、…、cn(t),直至rn(t)不能再被分解或者是满足给定的终止条件。通常rn(t)成为一个单调残余函数时退出循环,于是有:

(5)

式中:rn(t)代表信号的平均趋势。

3 Hilbert包络谱分析概述

Hilbert变换时,使测试信号产生一个90°的相移,从而与原信号构成一个解析信号,这个解析信号即为包络信号。

将一个原始信号x(t)的Hilbert变换H[x(t)]定义为:

(6)

H[x(t)]可以看作是x(t)通过滤波器的输出,则原始信号x(t)的解析信号z(t)可以表示为实部和虚部形式:

z(t)=x(t)+jH[x(t)]

(7)

Hilbert变换后的信号幅值记为a(t),a(t)定义为:

(8)

瞬时相位Φ(t)定义为:

(9)

由上述步骤可知,EMD方法所分解得到的IMF分量可以通过幅度或者频率进行调制,再通过Hilbert变换将信号高频振动分量去除,用含有缺陷激励分量的a(t)代替原始信号x(t)进行频谱分析,这样就可以有效提取故障信息,进行故障诊断。

4 滚动轴承故障诊断

笔者所研究的滚动轴承型号为6205,外径为52 mm,内径为25 mm,轴承节圆直径D为39 mm,滚动体直径d为7.938 mm,滚动体数量Z为9,轴承转速n为1 772 r/min,接触角α为0°,数据采样频率为12 000 Hz。

轴承内圈故障频率f为:

(10)

计算得到轴承内圈故障特征频率为159.95 Hz。

对轴承故障振动信号进行处理,得到故障振动信号时域图,如图1所示,同时得到频谱图,如图2所示。

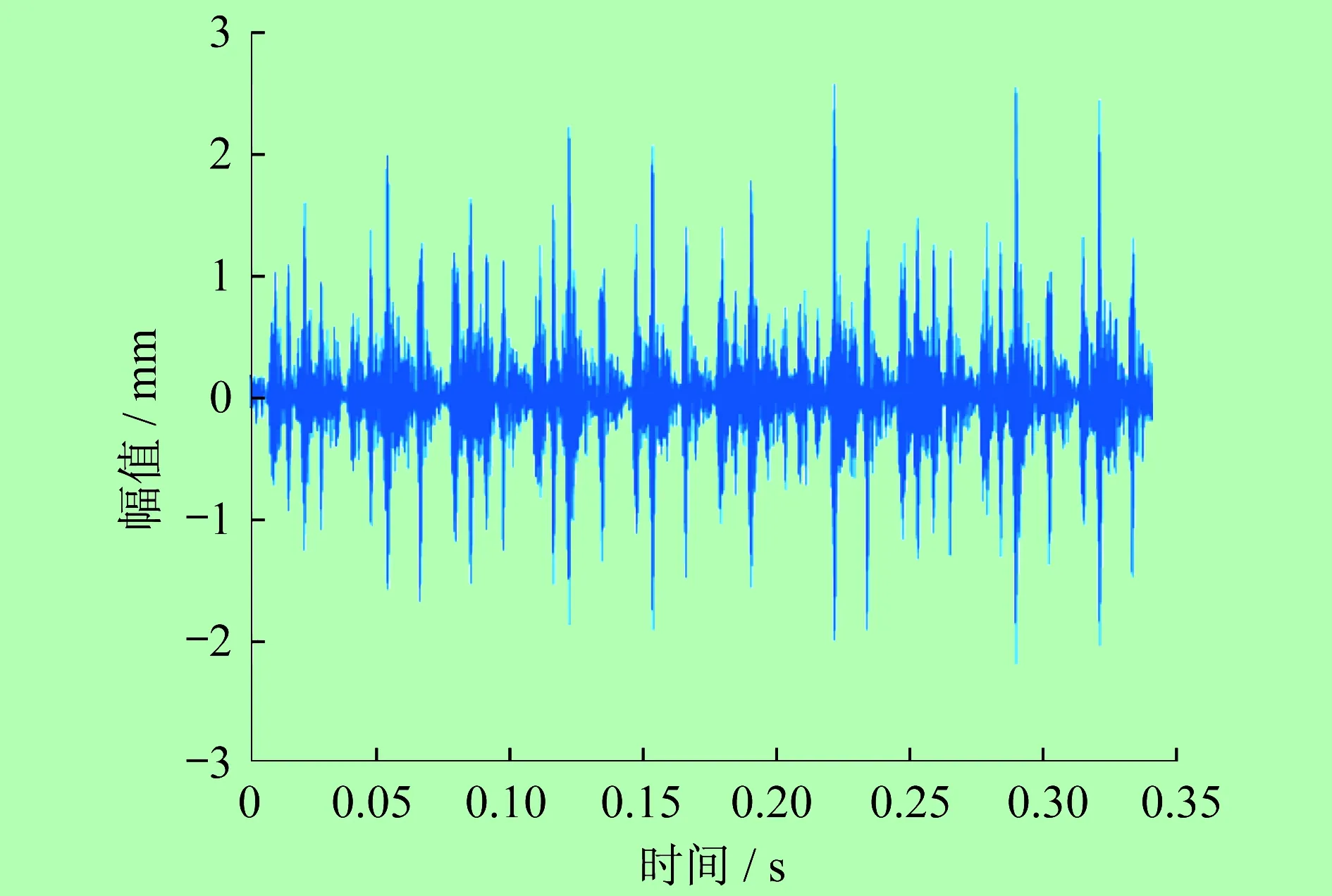
图1 故障振动信号时域图

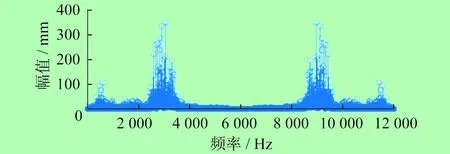
图2 故障振动信号频谱图

对滚动轴承故障振动信号采用EMD方法分解,得到各阶IMF分量,如图3所示。

基于EMD后得到的IMF分量,通过信号相关因数求解方程,可以计算出各阶IMF分量与原始信号的相关因数,见表1。

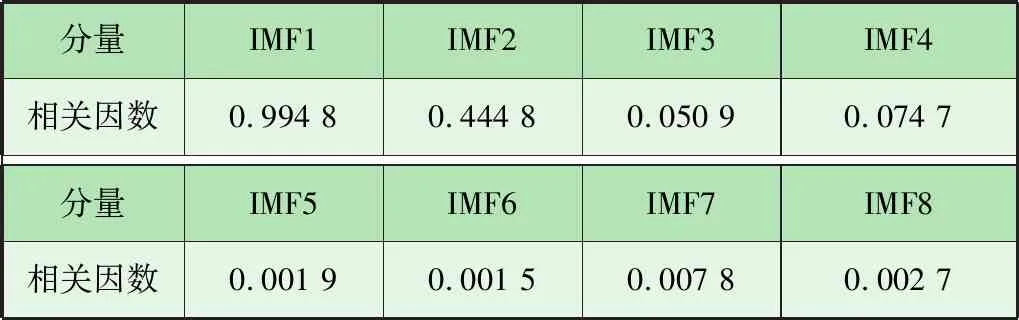
表1 各阶IMF分量与原始信号相关因数

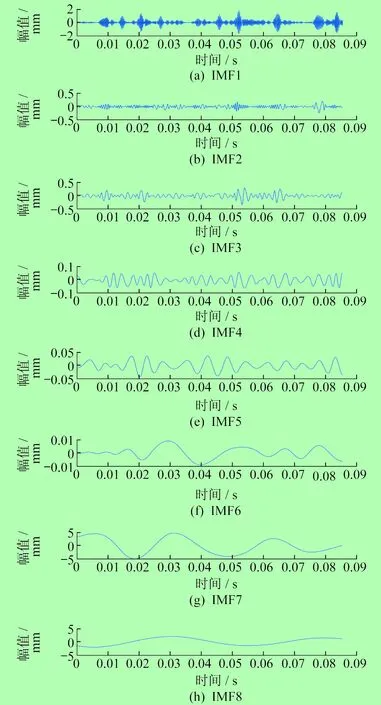
图3 故障振动信号各阶IMF分量

由表1可以看出,IMF1分量与原始信号的相关因数最大,因此,选取IMF1分量进行Hilbert包络谱分析,分析结果如图4所示。

由图4可以看出,滚动轴承的故障频率为159.4 Hz,这与理论计算所得的滚动轴承内圈故障频率159.95 Hz基本吻合。可见,所研究的滚动轴承内圈存在损伤。

5 结束语

笔者提出基于EMD与Hilbert包络谱分析的滚动轴承故障诊断方法,并对滚动轴承进行了故障诊断。这一方法通过EMD将非线性、非平稳振动信号分解出反映原始信号的IMF分量,应用Hilbert变换得到包络谱。试验结果表明,这一方法可以较为有效地获取滚动轴承的故障信息。

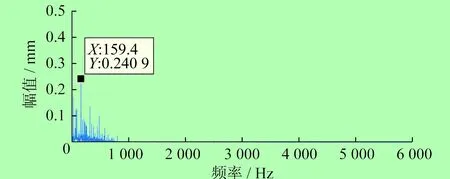
图4 Hilbert包络谱分析结果