RFID与GFSINS组合的地铁列车定位方法研究

兰州交通大学 机电技术研究所 兰州 730070

1 研究背景

随着我国城市化的持续快速发展,城市人口数量在不断增加,城市交通设施与城市化之间的矛盾正在逐步显现。在人们选择各种交通方式出行的同时,轨道交通越来越受到关注。从各国城市发展的实践来看,轨道交通因容量大、速度快、安全可靠、能耗低、污染少、准时舒适而受到公众的青睐。可见,城市轨道交通系统将成为我国公共交通的发展方向。轨道交通系统中的定位和导航是提高列车运行精度的重要部分。目前,地铁列车自动控制系统一般采用轨道和车辆设备实时定位列车,通过列车与轨道之间的信息传递,实现信息交换,实时控制列车。常用的列车定位技术包括卫星导航、惯性导航、查询应答器、里程表速度测量、多普勒雷达、轨道电路、航位推算、地图匹配等[1]。这些方法单独使用时都有一定的局限性,并且一旦出错,对乘客造成的危害是非常大的。为了提高地铁列车的导航定位精度,笔者提出射频识别(RFID)与无陀螺捷联惯导系统(GFSINS)组合的地铁列车定位方法,这样能够减小传感器的误差漂移积累,提高地铁列车定位的精度[2]。

2 原理概述

2.1 RFID定位

RFID定位主要由三个部分构成,分别为标签、读写器和中央信息系统。RFID系统通过使用阅读器和发射天线,将采集到的信息进行发送。当标签处于正常的工作状态时,内置的射频天线会将对应的编码信息发送至阅读器进行阅读及解码,最终使中央信息系统获得有效信息,并进行完整的识别和处理,以便完成对所采集信息的读写。RFID定位原理如图1所示[3-4]。

传统的捷联惯导系统(SINS)在确定载体的具体位置和姿态时采用加速度计测量物体运动的线速度,采用陀螺仪测量物体运行的角速度。GFSINS不再采用陀螺仪进行测量,而是使用加速度计代替陀螺仪,并且根据加速度计测量的比力进一步求解出载体的角速度,从而降低系统的复杂性,同时也能够节约成本。在对SINS加速度计进行安装操作的过程中,由于安装环境和安装者工艺水平的影响,并不能完全保证可以将加速度计安装到理想位置,进而造成安装于载体上的加速度计与质心位置有一定程度的偏移。当存在这种安装误差时,若载体做线性运动,则在进行测量时几乎没有影响;若载体在惯性空间内做旋转运动,则加速度计就会输出一定量的偏差,产生的这种偏差受载体旋转运动大小和加速度计安装误差大小两个方面的影响[5]。

图1 RFID定位原理

在SINS中,为达到理想的导航定位效果,必须采取一定的补偿办法修正该加速度计在空间运动时所产生的误差。而在GFSINS中,并不需要采用修正的方法补偿误差。因为GFSINS对于加速度值的测量是根据多个加速度计的合理设计并安装在载体非质心处来实现的,加速度计测量的加速度值可以转换为载体的角速度,这样就起到了SINS中陀螺仪的作用。由此可见,研究的重点是在省略陀螺仪的情况下如何获得旋转角速度和捷联矩阵[6]。GFSINS原理框图如图2所示[7]。

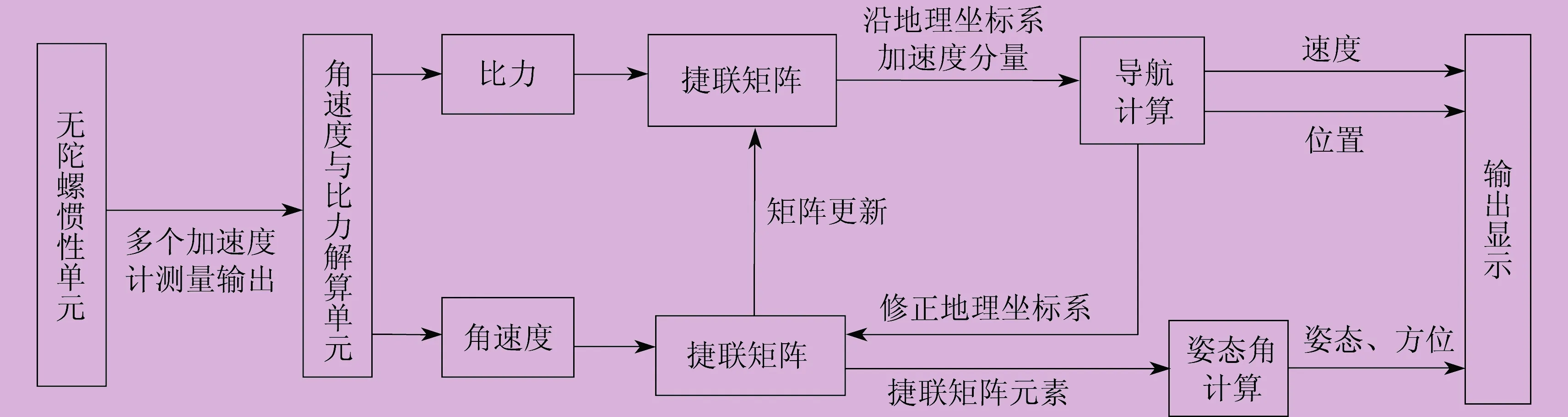
图2 GFSINS原理框图

2.2 RFID与GFSINS的组合

基于RFID和GFSINS的地铁列车定位方法,将地面RFID和列车控制系统有机结合在一起,无源标签以固定间隔放置,并且标签读取器和通信设备与安装在列车上的计算机相连。当地铁列车通过定位标签时,激活标签的有效工作状态,由此产生感应电流,同时车载读写设备读取标签中的位置信息数据,列车控制系统通过分析数据来实现定位[8]。

组合后RFID和GFSINS能够互不影响地正常工作。因为GFSINS具有较强的自主性和快速更新特性,所以一般归类为主体,而RFID则作为辅助。在对RFID和GFSINS进行组合时,需要充分考虑各个独立系统的工作特点,从而充分发挥各系统正常工作时的最优工作特性,因而需要设置合理的组合方案。根据目前地铁列车组合导航的功能要求,基于不同的组合深度,常采用松散组合和紧密组合两种不同的组合方式。

松散组合时,RFID和GFSINS阅读器均安装在地铁列车上。RFID和GFSINS在进行组合之后,各测量元件独立工作,彼此之间独立测量载体的数据信息,其中两个系统所测量的位置、速度及姿态等物理信息在输出时需要进行相减,进而在对应方程中对该测量值进行最优估计,最终系统对数据进行分析处理和反馈校正,输出组合导航的参数信息。在松散组合方式下,RFID辅助GFSINS工作。

紧密组合方式的复杂性和深度都甚于松散组合方式,在进行紧密组合时,采用GFSINS和RFID分别测算出地铁列车的伪距和伪距率,在此基础上将两系统测量值相减作为测量值,通过相应方程估算分析,进而达到最优输出。

以上两种组合方式无绝对优劣之分,具体采用哪种组合方式应该结合实际的项目需要进行综合分析。松散组合方式较紧密组合方式简单,有利于在工程中实现,并且松散组合方式中的两个系统能够独立对载体进行测量,当其中一个系统发生故障时,不影响另一个系统正常工作。因而出于综合考虑,笔者研究的地铁列车定位方法采用松散组合方式,既能有效提高定位精度和稳定性,又不会无谓增加运算量和提高系统的烦琐程度。

3 常用坐标系相互关系

坐标系转换是惯性导航的理论基础之一,在对GFSINS中的坐标系进行转换时,需要对常用坐标系相互关系进行描述。通过分析常用的惯性导航坐标系的相互关系及空间矢量的转换关系,得到GFSINS载体上不同空间位置加速度计的表达式。在此基础上,对求得的GFSINS角速度方程进行求解,从而进一步求取载体的姿态信息。

3.1 地心惯性坐标系(i系)-地球坐标系(e系)

地球自转的参考坐标系就是地心惯性坐标系,自转角速率就是地球坐标系相对于地心惯性坐标系的旋转大小,在地球坐标系中可表示为:

(1)

相应的转换矩阵为:

(2)

式中:ωe为地球自转角速度,ωe=7.27×10-5rad/s;t为时间。

3.2 地球坐标系(e系)-地理坐标系(L系)

对于地理坐标系相对地球坐标系的旋转角速度向量,可以分别推导出其在地球坐标系和地理坐标系中的分量表达式:

(3)

(4)

转换矩阵为:

(5)

式中:λ、φ分别为载体所处位置的经度和纬度。

3.3 地理坐标系(L系)-载体坐标系(b系)

(6)

由转动顺序可得变换矩阵:

(7)

(8)

4 惯导系统工作过程

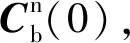
5 结束语

RFID与GFSINS组合的地铁列车定位方法相比传统的SINS,载体角速度和质心比力的获取方式不同。组合地铁列车定位方法能够为地铁列车提供连续的数据采集,可以全方面地将载体位置、速度、姿态等信息提供给列车运行控制系统,并且RFID定位有效避免了加速度计和陀螺仪在长期数据采集中的累积误差。组合地铁列车定位方法中,各个导航系统相辅相成、相互补充,提高了定位导航的精度[10-11]。对于组合地铁列车定位方法,笔者推导了载体上任意一点处的加速度计输出表达式,并以此作为理论基础,根据多个加速度计的联立方程组,为后续研究角加速度值和质心处的比力,进而获得地铁列车的线速度和位置参数提供了依据。