三条线段间数量关系的方法探讨

吴慧琳

(江苏省扬州市竹西中学 225000)

三条线段间数量关系的探讨是猜想证明题型的应用典范.一般无法通过一次性的操作解决，而要通过巧妙的方法加以转化.学生解决此类题型时，常找不到突破口，教师讲解时，应引导学生分析探讨的过程，使学生不仅知其然，还要能知所以然，以达到“授之以渔”的目的.下面结合具体事例谈谈三条线段间的数量关系探讨的研究方法和途径.

一、等积法得数量关系

例1在△ABC中，AB=AC，P底边BC上一点，PD⊥AB于D，PE⊥AC于E，CF⊥AB于F.探索PD、PE、CF三者的数量关系.

解连接AP.∵S△ABC=S△ABP+S△ACP，

∵AB=AC，

∴PD+PE=CF.

二、相似法得数量关系

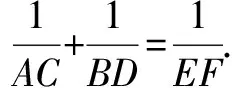
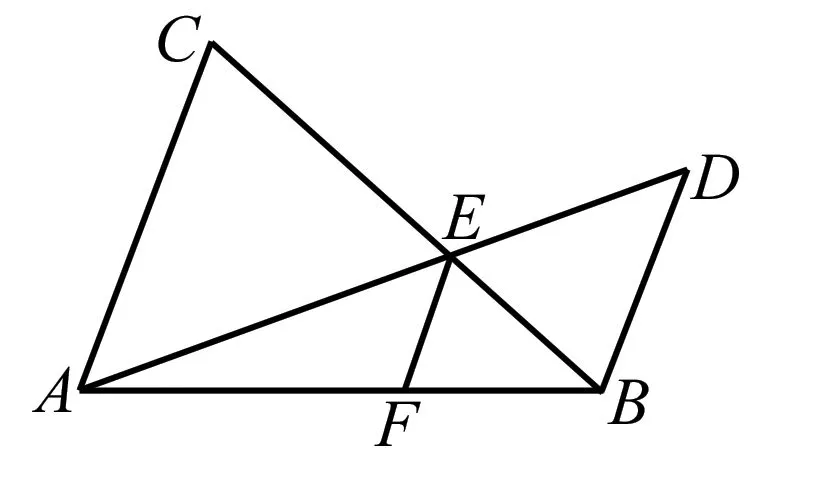
证明∵EF∥BD,

∴△AEF∽△ADB,

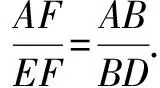
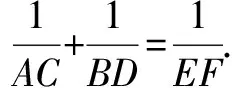
三、旋转法得数量关系

例3如图，在同一平面内，将两个全等的等腰直角三角形ABC和AFG摆放在一起，A为公共顶点，∠BAC=∠AGF=90°，若△ABC固定不动，△AFG绕点A旋转，AF、AG与BC的交点分别为D、E(点D不与点B重合，点E不与点C重合)，在旋转过程中，探索BD、CE、DE三条线段之间的数量关系．

解将△ACE绕点A顺时针旋转90°至△ABH的位置，则CE=HB，AE=AH，∠ABH=∠C=45°,旋转角∠EAH=90°.连接HD，在△EAD和△HAD中,∵AE=AH,∠HAD=∠EAH-∠FAG=45°=∠EAD,AD=AD，∴△EAD≌△HAD，∴DH=DE.又∠HBD=∠ABH+∠ABD=90°，∴BD2+HB2=DH2,即BD2+CE2=DE2.

四、补短法得数量关系

例4如图,正方形ABCD中,∠EDF=45°，且∠EDF的两边分别与AB，BC交于E，F. 试探究AE，EF，CF三条线段之间的数量关系，并证明你的结论.

解EF=AE+FC.理由：如图所示：延长BA至G，使AG=CF，连接DG.

∵在△ADG和△CDF中，AD=CD∠DAG=∠C=90°,AG=CF,∴△ADG≌△CDF(SAS)，

∴DG=DF，∠ADG=∠CDF.又∵∠EDF=45°,∠ADC=90°，∴∠DAE+∠CDF=∠ADG+∠DAE=∠GDE=45°,∴∠GDE=∠EDF.在△DGE和△DFE中，DG=DF，∠GDE=∠EDF，DE=DE，∴△DGE≌△DFE(SAS)，∴GE=EF.又∵AG=CF，∴EF=AE+FC.

五、截长法得数量关系

例5已知：如图，△ABC中，∠C=2∠B，∠1=∠2，求证：AB=AC+CD.

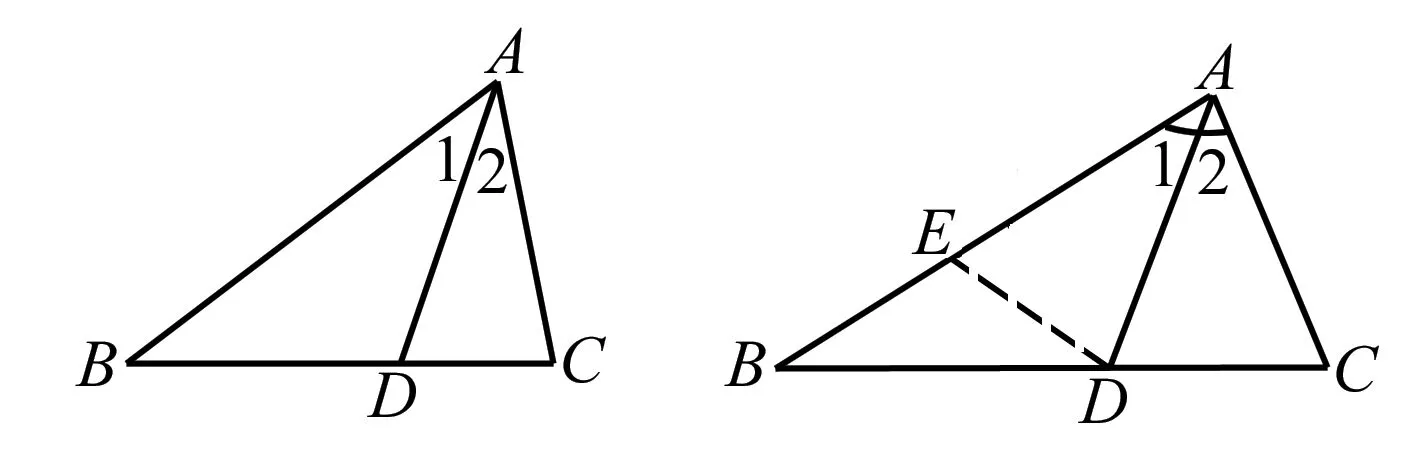
证明在AB上取AE=AC，连接DE，∵AE=AC，∠1=∠2，且AD=AD，∴△ACD≌△AED(SAS)，∴ED=CD，∠AED=∠C=2∠B，又∵∠AED=∠B+∠BDE，∴∠B=∠BDE，∴EB=ED，即△BED为等腰三角形.∴BE=ED=CD，∴AB=AE+EB=AC+CD.

六、构造法得数量关系

证明当0

∵∠ECG=45°，∴∠EHG=45°，∴∠EHG=∠FCG.

在△EGH和△FGC中，∠EGH=∠FGC，BE=FG，∠CHG=∠GCF，∴△EGH≌△FGC.∴EH=FC.

本题也可进行拓展：当t≥4时，CE、CF、CG的数量关系是否发生变化，并说明理由.

通过上述的几种方法可知，探讨三条线段间的数量关系，需认真分析题目中的已知条件，巧添、巧截、巧补、巧转，寻求解决问题的最佳途径，掌握住方法，就能做到会一题，通一类，知一片，使得复习效果事半功倍.