辨识全等与旋转 方知旋转有奇效

摘 要：旋转思想与全等思想本质上有着密切的关联性.一般而言，学生运用旋转思想证明旋转背景下的全等问题，要比用全等思想证明困难得多，学生易单纯地从全等模式下进行证明，极易产生漏解（遗漏线段位置关系）.对此，对于旋转思想的培养，要加强利用概念要素教学探究性质，以利于学生对旋转法的理解运用.

关键词：旋转问题;旋转法;全等法;思辨关系

作者简介：程志南（1964-），男，浙江瑞安人，专科，中学高级教师，研究方向：初中数学教学与解题研究.

学习人教2013年版教科书的九年级学生，在求解有关旋转类型的全等问题时，习惯用全等的视觉看待解决.缘何如此？究其原因，我们发现，这是由于旋转与全等有着共同的属性特征，都是关于两个图形之间能够完全重合的全等关系;又由于旋转与全等的证明过程之推理表达形式极其类似，都是在全等的过程推理模式中进行;再由于旋转知识是初学初用，而全等知识却普遍存在和广泛应用，学生全等思想烙印深刻;还由于旋转涉及图形的运动，而运动的图形使线段之间、角之间的关系变得复杂抽象.如何教学才能使学生自觉地运用旋转思想解决有旋转背景的全等问题？本文试图从旋转与全等的关系，学生的学习方式习惯等诸方面分析产生的原因，以及对教学的一些思考.

1 问题提出

图形的旋转与全等有着千丝万缕的联系，旋转也是一种全等变换，可谓旋转中必有全等，全等中一定条件下有旋转背景.

学生用旋转思想证明旋转背景下的全等问题，要比用全等思想证明困难，求解时习惯用全等视觉一味地只关注静态下图形全等而缺乏运动观点，不能自如地运用旋转性质定量、定性描述推理，造成对图形只作定量分析无定性描述，导致解题走进死胡同，结论写不全.作为教师，常困惑于学生学习方法死，固守已有的全等思维模式，运动观点、发散思维与创新能力差，如何让学生求解此类问题时，自觉地运用旋转思想解决呢？

2 试题呈现

题1 如图1，点K是正方形ABCD内一点，以AK为一边作正方形AKLM，使点L，M在AK同旁，连接BK和DM，试用旋转思想说明BK与DM的关系.

这是我县九年级中考模拟试题.试题立足教材“旋转”章节，关注学生对旋转知识掌握与运用情况，考查感知运动观点，运用旋转思想解决问题的能力.从题目数学对象点、线、角、形，需从图形位置和数量关系两个角度描述.但从阅卷情况看，这一考查目标不理想，学生基本从全等角度入手，只判断线段BK与DM的数量关系而遗漏位置关系，鲜有运用旋转思想解决，说明很多学生概念理解不全混淆不清，或题意理解不清漏写结论，暴露了学生用运动观点分析解决问题意识不强，同时也从教学方面说明了教师在教学中渗透旋转观点的教学观重视不够.

3 解答情况

3.1 多数学生从全等角度解答

解析 因为四边形ABCD和AKLM是正方形，

所以AB=AD，AK=AM，且∠BAD=∠KAM=90°.

所以∠BAD-∠KAD=∠KAM-∠KAD.

即∠BAK=∠DAM.

所以△ABK≌△ADM（SAS）.

所以BK=DM.

3.2 鲜有学生从旋转角度解答

解析 因为四边形ABCD和AKLM是正方形，

所以AB=AD，AK=AM，且∠BAD=∠KAM=90°.

所以△ADM是以点A为旋转中心，∠BAD为旋转角，由△ABK旋转而成，所以BK⊥DM且BK=DM.

由全等法只获得数量关系，而旋转法既获得定量又获得定性关系.其实，全等法也可得位置关系.只要延长BK交DM，得两个对顶三角形，由△ABK≌△ADM和对顶角相等，同样可得BK⊥DM.

题目要求从旋转角度说明线段关系，然而多数学生全然无视不顾，直奔两个三角形全等获得数量关系，不会从数量和位置关系两角度刻画图形性质，仅从一角度写结论.可见，学生求解时眼中只有全等而无旋转，空间想象匮乏.运用旋转思想处理全等问题，需要有一定的空间观念和运动观点支撑，这正是学生的短板，需要“修补”加强.

4 原因分析

4.1 全等思想根深蒂固

旋转对全等有密切的依存关系，有旋转背景的图形一定存在全等效果.人教2012年版教科书把“全等三角形”编排在八年级上，一年后安排九年级上学习“旋转”.这样，学习全等后的几何学习中，全等知识普遍存在和广泛应用，全等思想运用几乎“如影随形”无处不在，使用率极高.而后续学习的旋转知识是初学初用，且图形需要有旋转背景特征条件才能用旋转思想处理，使用率低于全等.因此学生全等思想烙印深刻，全等意识强于旋转意识，在处理两条线段关系时，腦海里首先释放的是全等策略强信息，在此信息牵引下自然而然地运用全等思想解决问题.

4.2 思维定势产生负迁移

由于全等思想运用的普遍性和先入为主的观念，全等思想占据主导地位，形成潜意识下思维习惯.学生学习知识单一肤浅，在惯性思维作用下，后继运用新知识“旋转背景下的全等”，受已有知识经验全等思想运用比较熟练的干扰，产生过度依赖，引起思维僵化，不能从运动观点出发，多角度、全面整体地看问题.在解决此类问题时，受思维定势消极影响，“独此一家，别无分店”，眼中只有全等，不能用运动观点从旋转角度思考，妨碍了运用旋转思想解决问题的策略.教育心理学认为，产生错误原因是负迁移作崇.

4.2.1 旋转与全等的属性特征一致造成负迁移

人教2012年版义务教育教科书八年级上第31页定义全等：“形状、大小相同的图形放在一起能够完全重合的两个图形叫做全等形”;而把一个平面图形绕着平面内的某个点转动一个角度，旋转前后的两个图形形状、大小相同，完全重合，是全等形.简言之，旋转与全等都有着两个图形能够完全重合的全等形关系共同属性特征.

4.2.2 旋转与全等的对应元素性质相同造成负迁移

全等的两个三角形对应线段相等，对应角相等;同样，基本图形经过旋转，旋转前后的两个图形的对应线段相等，对应角相等.

4.2.3 旋转与全等的证明过程相近造成负迁移

旋转与全等的证明过程，其书写推理表达形式极其类似，都是在全等推理模式中进行，极易造成负迁移.学生受全等思想定势思维的消极影响，求解时容易走入全等误区.如题1，全等用“边角边”判断，旋转同样用类似于“边角边”模式获得.

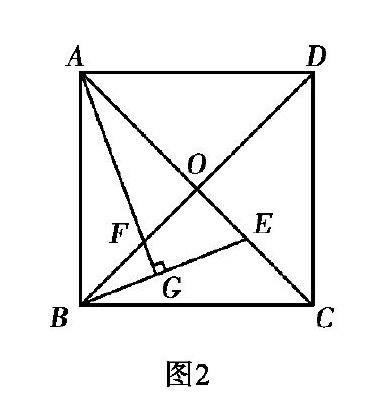
题2 如图2，正方形ABCD的对角线AC，BD相交于点O，E是AC上一点，过点A作AG⊥EB，垂足为点G，AG交BD于点F，求证：OE=OF.

解法1（利用全等思想证明）因为四边形ABCD是正方形，所以AC⊥BD，OA=OB.

所以∠AOF=∠BOE=∠90°.

因为∠AGB=90°，所以∠BEA+∠EAG=∠AFO+∠EAG=90°.

所以∠BEA=∠AFO.

所以△AOF≌△BOE（AAS）.

所以OE=OF.

解法2（利用旋转思想证明）因为四边形ABCD是正方形，所以AC⊥BD，OA=OB.

因为∠AGB=90°，所以∠BEA+∠EAG=∠AFO+∠EAG=90°.

所以∠BEA=∠AFO.

故可以点O为旋转中心逆时针旋转90°，使Rt△OAF重合于Rt△OBE，所以OE=OF.

全等策略是根据正方形性质，利用AAS判定全等，再用全等性质获解;而旋转策略也是根据正方形性质，用类似于AAS模式推理两个三角形重合，得对应边相等.两相比较，只不过旋转要特别证明有一对旋转角相等，在推理过程中体现出来.可见，旋转与全等的证明过程何其相似.

4.3 学生常常纠结于旋转证明如何表述

运用旋转知识解决问题时，学生常常疑问：在解题时怎样提及旋转？我用全等证明了，但题目要求“用旋转思想”，该怎样表达呢？是证明它旋转，还是用旋转性质去证明？

学生纠结的问题，其实质是畏惧旋转证明的书写形式.对学生而言，全等证明容易上手，而旋转证明相对棘手.由于思考问题的局限性，不善于用运动眼光看待问题.旋转变换本质就是图形运动的一种形式，因为旋转，所以抽象，抽象使问题变得复杂困难.因此，相较于全等书写表达形式，学生不习惯用旋转书写形式推理表达，且有畏忌心理，害怕写不好，故喜好从全等角度进行推理表达.

5 教学思考

教學旋转变换性质，要紧扣三要素进行，以彰显变换特性，体现点、线、形变换的一致性，强化研究视觉的关联性，需要强化图形变换的过程性教学，重视几何语言学习.

5.1 学会利用三要素描述旋转过程

概念是基础，三要素是旋转概念的基石，是重中之重.教学旋转概念时，依据教材“思考”材料，借助具体物体（时钟）的支持，依托课件操作演示，直观感知旋转变换是由一个图形改变为另一个图形，在改变过程中，原图上所有点都绕某个固定点按同一方向转动同一个角度，三个要素揭示定义实质，从而明确三要素.因此，要清楚地描述旋转现象，首先要说明旋转中心，然后说明旋转方向和角度.以时钟指针旋转为例，你能用旋转三要素描述指针的旋转吗？然后进行辨识旋转中心、旋转角和描述旋转现象的练习，加深理解.

5.2 利用旋转概念要素思考研究旋转性质的教学

性质是运用于解题的依据.只有深刻理解了旋转不变性，才会具备运用旋转思想解决问题的意识，以及正确灵活地创新运用.数学本质是数学思想的教学，那么，旋转本质就是旋转思想的教学.教学旋转性质时，充分依托教材学习材料，丰富并发展.用猜想、测量、验证、证明的教学方式引领学生研究旋转性质.

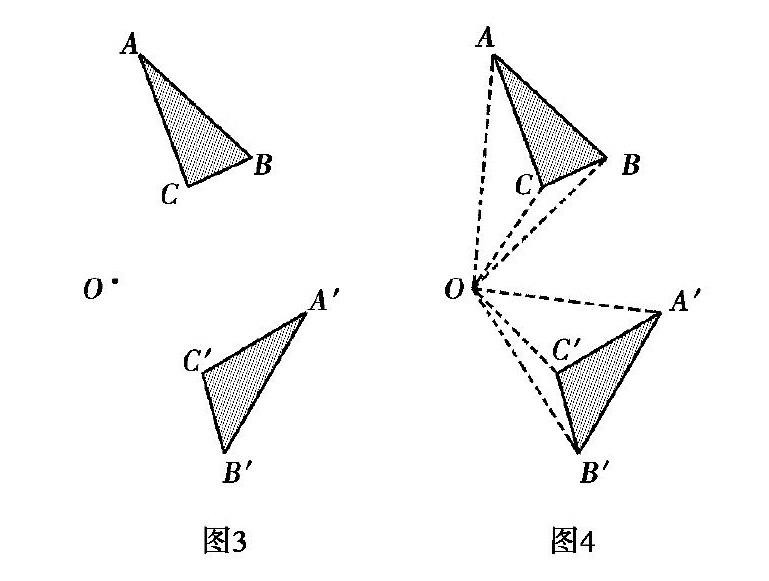
探究 如图3，在硬纸板上，挖一个三角形洞，再另挖一个小洞O作为旋转中心，硬纸板下面放一张白纸.先在纸上描出这个挖掉的三角形图案（△ABC），然后围绕旋转中心转动硬纸板，再描出这个挖掉的三角形（△A′B′C′），移开硬纸板[1].你能得出它们哪些不变性？

学生独立思考后，小组合作，用符号语言写出图中整体和对应要素之间的数量和位置关系.点的旋转轨迹是圆弧路径，因此，图形上点与旋转中心连线即为半径，如图4.

追问1：△A′B′C′可以看成△ABC经过怎样的运动得到的？

追问2：观察旋转前后的两个图形，你能立即得出它们有哪些不变性吗？

追问3：总结得到的结论，从三要素出发，对应点的不变性怎样体现？

追问4：你认为研究旋转的性质就是研究什么？

追问5：你认为对应元素有哪些？它们在形状、大小、位置关系上有哪些不变性？

这里的教学处理，就是引导学生从概念出发思考性质，也就是利用旋转三要素研究性质.体现两点[2]：①由点到形研究.先从图形上特殊点（线段端点）变换过程出发，由特殊到一般去研究整体.让学生知道，旋转性质就是旋转前后两个图形的关系，是两个图形的形状、大小和位置关系;②思考的有序性（逻辑性）.由一组对应点性质（即对应点到旋转中心距离相等，对应点与旋转中心连线所成的角等于旋转角），再到两组对应点性质（即两组对应点分别与旋转中心连线所成的角相等），最后利用已确定的要素（点、线、角关系）对象，明确研究图形的全等关系.

追问6：怎样验证上述猜想的正确性？这一发现对于任意三角形的任意旋转都成立吗？

学生猜想和测量后，利用几何画板给出一些数据进一步操作验证.几何图形性质，只靠猜想和有限的数据验证远远不够，利用相关定理进行推理验证，才是科学可信的.

证明 因为A和A′是对应点，由对应点的定义可知OA=OA′，同理OB=OB′，OC=OC′，即对应点到旋转中心的距离相等.

因为∠AOB=∠A′OB′，所以∠AOB+∠BOA′=∠A′OB′+∠BOA′.

所以∠AOA′=∠BOB′.

同理∠AOA′=∠BOB′=∠COC′.

即任意一对对应点和旋转中心的连线所夹的角（旋转角）相等.易证△AOB≌△A′OB′.

所以AB=A′B′，同理BC=B′C′，CA=C′A′.

所以△ABC≌△A′B′C′.

即旋转前后的两个三角形全等.

问题1-5体现了探索发现，问题6体现了合情与逻辑推理，突出：①点旋转确定形旋转效果，将研究形旋转转化为研究点旋转;②一个基本点（旋转前后两个图形对应点绕旋转中心旋转了相同角度）统领旋转全局的教学思路.让学生亲历了性质发现、概括和验证过程，帮助深刻理解和掌握性质，发展归纳和合情推理能力.其中，“旋转前后两个三角形全等”性质的证明，需要通过添加辅助线（点运动半径）构造获得，这又为后续解决旋转全等问题提供了方法策略.

5.3 怎样用旋转思想解决几何问题

以一道习题的解析为例进行说明.

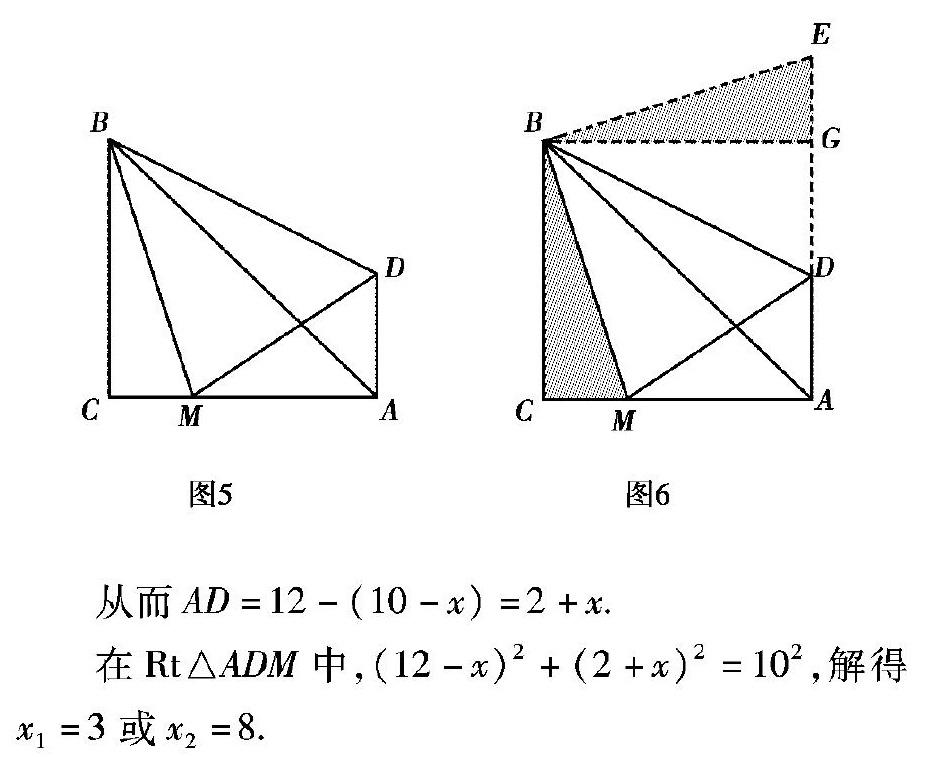
题3 如图5，等腰Rt△ABC中，M为AC上一点，∠DBM=45°，且AD⊥AC，AC=BC=12，DM=10，求CM的长.

解法1 如图6，延长AD，作过点BG⊥AD交AD延长线于点G，截取GE=CM.

易证四边形ACBG.

所以△BGE≌△BCM，△BDM≌△BDE.

设线段CM=x，则EG=x，DG=10-x.

从而AD=12-（10-x）=2+x.

在Rt△ADM中，（12-x）2+（2+x）2=102，解得x1=3或x2=8.

解法2 将△BCM绕点A逆时针旋转90°到△BGE，连接DG.由旋转性质易知△BGE≌△BCM，∠CBG=90°.

所以∠BGE=∠BCM=90°，EG=CM.

由等腰Rt△ABC和AD⊥AC，易证四边形ACBG是正方形.

所以∠BGD=90°.

所以∠BGD=∠BGE=90°.

所以D、G、E三點在同一直线上.下同解法1.

由于旋转涉及图形运动，运动的图形使线段之间、角之间关系变得复杂抽象，但旋转却能够把如同散沙般的条件聚拢利用，有利解决问题.那么，如何想到用旋转方法呢？

5.3.1 如何添辅助线

这个问题等同于怎么想到旋转法.本题条件十分分散，不易直接求出CM，如何将关联线段集中到同一个三角形中，是解决问题的关键.等腰直角三角形其实是由正方形沿对角线折叠后得到的，我们想到，不妨将这个过程还原，即构造出原来的正方形，同时可以将△BCM绕点B逆时针旋转90°，如图6.

这是一个非常熟悉的图形，通过旋转构造出一对全等三角形△BCM和△BGE，同时还得到另一对全等三角形△BDM和△BDE，思路由此打开.

5.3.2 如何表述辅助线的作法

显然，两种解法都体现了旋转思想构造全等三角形的思路，然而，辅助线作法的表述截然不同.

解法1体现旋转思维非旋转作图.证明过程中没有表述为旋转，通常用作出辅助线后再证全等方式来达到旋转效果.说明作辅助线的具体内容如：“过某点作××的平行线（或垂线），交××于×点”“延长××到×点，连接××”“在××上截取××=××，连接××”“作∠×××=××度”.

解法2体现旋转思维旋转作图.借助旋转思想对图形元素间的关系进行定性分析探寻思路构造全等三角形，证明过程中利用旋转三要素表述旋转作图，但需要说明三点共线，而这恰是学生的软肋.

如何掌握旋转的方法，使学生逐步添加辅助线，这些都是有规律可循的.由此，教学时，必须向学生讲清旋转作图的两种方法，会正确表达旋转后的结果，注意规范辅助线的表述，规范证明的书写格式.

通过习题教学，甄别旋转背景下全等问题的两种解法，领会旋转法实质是从动态视角探究问题，在变化中发现规律的一种解题方法;理解当图形条件过于分散，无法有效利用时，就需要移动图形，将部分图形改变位置后重组优化，有利发现隐含条件，抓住问题的实质关键，而移动图形的手段就是三种变换;明确当图形中只要存在共顶点的等线段时，就可以实施旋转变换，体会创新妙用旋转变换解决问题的奇效.

参考文献：

[1]林群.人教版义务教育教科书九年级上册（2012年版）[M].北京：人民教育出版社，2013.

[2]姜昊. “图形的旋转”教学设计[J]. 中国数学教育，2018（09）：52-55+64.

（收稿日期：2019-08-19）