追本溯源巧解最值

丁 洁

几何问题如果加上“运动”元素，就会由于图形的运动而产生许多“变量”。“运动中变量的最值问题”或“运动中的不变量”往往是中考命题的热点。解这类几何最值问题，如果缺少必要的基础知识与基本能力储备，往往难以找到突破口。下面我们就通过一道几何最值问题的解析，来追本溯源。

例 如图1，在平面直角坐标系中，直线l与y轴的正半轴的夹角为20°，点A在直线l上，OA=2，M为直线l上一动点，P、N是y轴上的一动点，求AP+PM+MN的最小值。

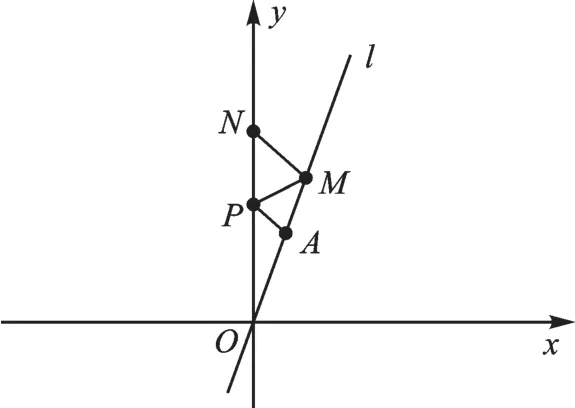
图1

【错解】从“最小值”出发，认为：过点A作PA⊥y轴于点P，这样AP就取得最小值；在此基础上，过P作PM⊥l于点M，这样PM就取得最小值；然后在此基础上，过点M作MN⊥y轴于点N，此时的MN取得最小值。最后，将所求得的AP、PM、MN三条线段相加，得出结果。

【错因】上述“解法”立足于孤立的线段去思考最值，忽视了“AP+PM+MN”的整体性，这样一来，思考就片面化了，隐含的错误就是“AP+PM+MN”这个整体取得最小值时，AP并非一定同时取得最小值。

【正解】对于多条折线求和问题，我们应将“代数求和”转化为“几何求和”，先借助“轴对称”，将同侧线段转变到异侧，再“化折为直”，完成求和。

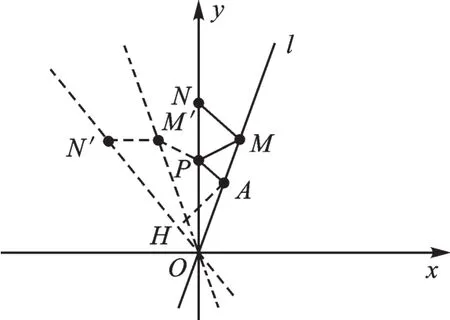
图2

如图2，以点P所在直线（y轴）为对称轴作点M的对称点M′，则PM′=PM。以点M′所在的直线OM′为对称轴作点N的对称点N′，则M′N′=M′N=MN。∴AP+PM+MN=AP+PM′+M′N′。

这样就可“化折为直”，最值一定是当A、M′、N′在一条直线上时取到。再根据“垂线段最短”，过点A作AH⊥ON′于H，当点N′落在点H处时，AP+PM+MN取得最小值。

由题意，不难得到∠AON′=60°，再根据OA=2，可求得AH=，即AP+PM+MN的最小值为。

【点评】本题难度较大，对同学们的思维能力要求较高。同学们不妨尝试以下变式训练，以加深相关理解。

变式1如图3，在平面直角坐标系中，已知A（8，0），B（2，0），经过原点的直线l与x轴的正半轴的夹角为30°，P是直线l上一动点，求PA+PB的最小值。

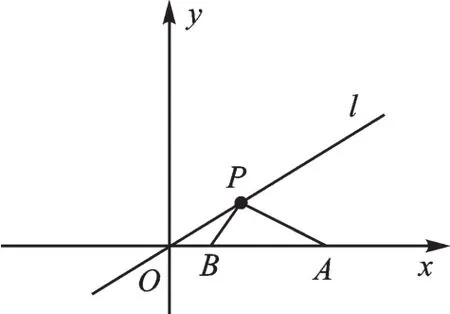
图3

变式2在平面直角坐标系中，已知A（8，0），B是x轴上的一个动点，经过原点的直线l与x轴的正半轴的夹角为30°，P是直线l上一动点，求AP+BP的最小值。

变式3在平面直角坐标系中，已知A（8，0），B是x轴上的一个动点，经过原点的直线l与x轴的正半轴的夹角为30°，P是直线l上一动点，Q是直线l上一定点，且OQ=2，求AP+PB+BQ的最小值。

变式4在平面直角坐标系中，已知A（8，0），B是x轴上的一个动点，经过原点的直线l与x轴的正半轴的夹角为20°，P是直线l上一动点，Q是直线l上一定点，且OQ=2，求AP+PB+BQ的最小值。

【解析】变式2、3、4没有直接给出图形，同学们可以自己试着画图。此外，这组题由易到难，同学们在看具体解析之前，可以先独立尝试解决。

变式1属经典的“将军饮马”模型，利用轴对称的性质，将同侧两线段转化为异侧两线段，从而“化折为直”，利用“两点之间，线段最短”求得最小值。

变式2延续了变式1的思维，再结合“垂线段最短”可得最小值。

变式3、变式4由“两条线段之和的最小值”拓展为“三条线段之和的最小值”，可继续沿用“将军饮马”模型，多次作对称线段以求解。这两题与前面的例题解法类似，同学们不妨试一试，以检验自己对例题的理解程度。

【点评】例题难度较大，也许你不能一下子理解。而变式可以帮助你更好地理解与掌握解决此类问题的途径。变式1对你而言估计没有难度。变式2中，定点B变为x轴上一动点，难度略有提升。根据“点动成线”的思路，x轴即为所有动点B的集合，所以作点A关于直线l的对称点A′，A′B的最小值就是A′到x轴上的点的距离的最小值，“垂线段最短”的“加盟”，使得问题走向深入。变式3、变式4由“两条线段之和的最小值”拓展为“三条线段之和的最小值”，有了变式1、变式2的铺垫，相信同学们一定能想到通过类似方法去“化折为直”。

数学学习需要一定的连贯性与灵活性，上面的一组变式训练题由易到难，一脉相承。相信同学们在逐一解答的过程中，一定会感受到其中的关联，从而领悟到“化定为动”的命题思路及解题过程中“化折为直”的奥秘。这个案例给我们这样的启示：经典题犹如题根，抓住题根，就等于抓住了整个题系。我们要追本溯源，进行变式拓展及生长。切实理解问题的实质，可以追求大道至简，实现“做一题，会多题”“会一法，得通法”，这样一来，我们的复习就更有效，从而收到事半功倍的效果。