顺藤摸瓜 寻求突破
陆金花
图形变换是中考考查内容之一,可能以填空、选择、解答题等题型呈现,具体解答时有时还需添加辅助线。下面,我们以一道图形变换的中考题为例,来探讨如何顺藤摸瓜,找到解决这类问题的突破口。
例1如图1,在Rt△ABC中,∠B=90°,AB=,BC=将△ABC绕点A按逆时针方向旋转90°得到△AB′C′,连接B′C,则sin∠ACB′=_______。(3分)
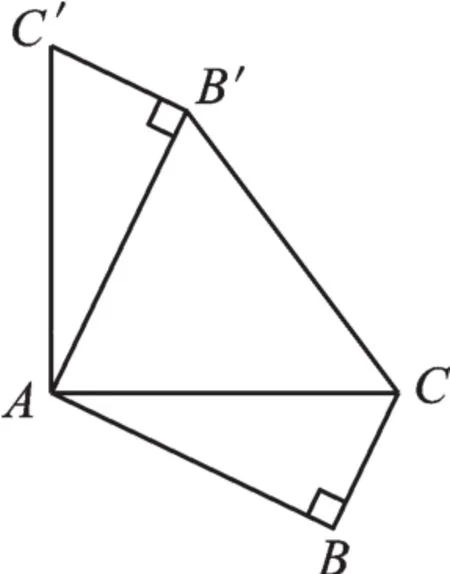
图1
虽然本题为一道填空题,做对得3分,做错或不做不得分,但我们在分析问题时同样也可以剖析其考查的知识点,踩点进行分析解答,以便顺藤摸瓜,得到正确答案。
【考点】旋转变换、勾股定理、相似三角形的判定与性质、锐角三角函数的定义。
【解析】旋转是图形变换中的一种,旋转问题指的是一个图形绕着某个点按顺时针或逆时针方向转动一定角度后,得到新的图形,然后求解旋转前后图形的一些线段、角及与之相关的量。处理这类问题的关键在于找到旋转前后相等的量。本题是旋转、勾股定理、三角函数、相似的综合。显然,由旋转知△ABC≌△AB′C′,而要求sin∠ACB′的值,则将∠ACB′放置于一个直角三角形中,利用所学知识进行求解即可。
解:在Rt△ABC中,由勾股定理可得AC=5。
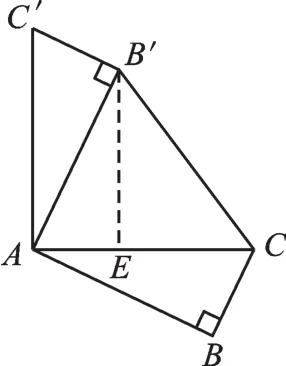
图2
易证△B′AE∽△ACB,从而根据“相似三角形的对应边成比例”可求得AE=2,B′E=4。
∴CE=AC-AE=5-2=3。
在Rt△B′CE中,由勾股定理可得B′C=5。
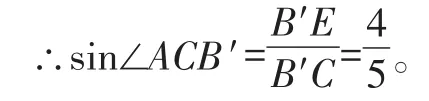
【点评】通过上例,不难看出,对于此类较复杂的问题,我们需要踩点分析,才能顺利找到解题的突破口。比如,已知一个直角三角形(△ABC)的两边长,可以根据勾股定理求得第三边的长。再如,要求一个角(∠ACB′)的正弦值,需构造直角三角形(△B′CE)。此外,旋转将图形中的基本元素(线、角)进行了关联,而“相似三角形的判定与性质”则是求解这类几何计算题的常用手段。只要我们善于抓住本质,踩点分析,就一定能顺利寻求突破。

