传递闭包的Matlab实现

孙翠先，张 健，吴焕春

(唐山学院 基础教学部，河北 唐山 063000)

0 引言

集合A上的二元关系R的传递性描述了序偶之间的内在联系。当A的元数|A|比较小(|A|≤4)时，可通过序偶法、关系矩阵法或关系图法判定，计算量不大，人工判定可以完成。但当|A|较大时，不论上述三种方法哪一种，人工计算量都非常巨大，基本上不可能完成。而求关系R的传递闭包t(R)时，当R不具有传递性，就需要通过不断添加新序偶使之具备传递性为止。因此当|A|较大时，求t(R)变得非常困难。此时Warshall提出了一种算法[1]。本文在Warshall算法基础上，利用关系矩阵，借助数学软件Matlab，给出求t(R)的优化算法。此法实现了传递闭包的Matlab计算，最大优点是对|A|无限制，程序简便易操作，最重要的一点是给出了新添加的序偶矩阵。

1 算法

1.1 符号引入

给定集合A上的一个二元关系R，设MR为R的关系矩阵，MR=(rij)，这里rij只取0或1，它是一个布尔矩阵。设集合A={a1，a2，…，an}，t(R)的关系矩阵为Mt(R)。

1.2 传递闭包的矩阵性质

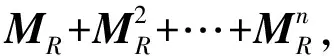
1.3 Matlab程序

Mt=R；

a=size(R)；

for k=1∶a

for i=1∶a

for j=1∶a

Mt(i，j)=max(min(Mt(i，k)，Mt(k，j))，Mt(i，j))；

end

end

end

Mt

Mt-R=NR

还原得t(R)。

2 实例模拟求传递闭包

给定A={a，b，c，d，e，f，g，h}，|A|=8，R={，，，，，，，}。

在Matlab R2007b下运行：

>>Mt=MR；

>>a=size(MR)；

>>for k=1∶a

for i=1∶a

for j=1∶a

Mt(i，j)=max(min(Mt(i，k)，Mt(k，j))，Mt(i，j))；

end

end

end

>>Mt

Mt=

>>Mt-MR

ans=

ans即为新添加的序偶矩阵。新添加的序偶集合为

NR={，，，，，}，结果t(R)=R∪NR。

3 结语

实例中全域关系|EA|=64，而|R|=8，|R|占|EA|的百分比只有12.5%，此时可以人工手算。但当|R|占|EA|的百分比只有30%以上时，人工求t(R)几乎不可能实现，而此时突显本文给出的方法的优越性。