泵轮式混合澄清槽混合室单相流的CFD模拟

刘继连，纪雷鸣，李少伟

(1.中国核电工程有限公司，北京 100840；2.清华大学 核能与新能源技术研究院，北京 100084)

混合澄清槽是核燃料后处理厂常见设备之一[1-3]。液-液萃取过程中，有机相与水相首先在混合澄清槽的混合室内充分搅拌混合，传质接近平衡状态的混合相进入澄清室澄清并形成逐级逆流接触[4-5]。混合澄清槽具有萃取级效率高、适应性强、放大简单与操作性强等优点[6]。

泵轮式混合澄清槽采用具有抽吸力的泵轮搅拌装置，运行更稳定，并极易在较宽流量范围内放大，因此，在国外核燃料后处理厂中被广为采用[7-8]。泵轮式混合澄清槽的水相和有机相均从混合室底部的前室进入，然后由泵轮吸进混合室中。混合室内混合相的密度比有机相的密度大，因此需要泵轮抽吸力来克服二者的密度差才能使两相逆向流动；另外，泵轮可以在泵轮与混合室侧壁之间形成内循环，从而提高混合澄清槽的萃取效率[9-10]。

混合澄清槽设计中常用到CFD软件[11-14]。CFD模拟不仅能够利用计算机进行数值计算，节省人力物力及设备投资，而且可以揭示试验无法观测到的流体内部的流动混合规律与压力分布规律。试验以CFD软件对混合澄清槽混合室内的单相流进行数值计算，并将计算结果与试验数据进行对比，验证数值计算结果的准确性。

1 混合室结构

泵轮式混合澄清槽的混合室结构如图1所示。

待混合的轻相和重相进入混合室底部的前室，在搅拌装置的抽吸作用下，两相从混合室与前室之间的圆孔进入到混合室内，并由搅拌装置进行混合。

图1 泵轮式混合澄清槽混合室示意

2 计算模型及方法

2.1 基本计算方程

描述混合澄清槽内液相流动的基本方程有连续性方程和动量传递方程。连续性方程是描述宏观流体的最基本方程，它的本质是质量守恒，对于不可压缩流体，其表达式为

(1)

动量传递方程是描述流体运动的方程，一般采用Navier-Stokes方程。混合澄清槽内搅拌强度较大，为湍流流动，而湍流的描述模型很多，一般在有较大旋涡情况下，采用雷诺应力模型。对于混合澄清槽所选择的运动方程及雷诺应力方程分别为：

(2)

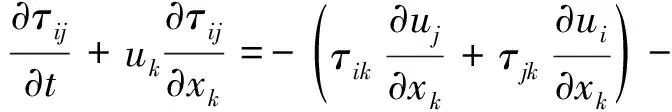
(3)

其中：

这些基本方程可以描述混合澄清槽内液体的流动过程，但复杂度很高，只能通过数值方法进行求解。数值求解需要对求解区域进行网格划分，在网格划分基础上对上述方程进行离散化处理，进一步进行数值求解。

2.2 几何模型和网格

2.2.1 几何模型的建立

对所求解的混合室及泵轮进行几何建模，其三维模型如图2所示。

图2 混合澄清槽的三维几何模型

混合室为170 mm×170 mm×170 mm的正方形；混合室中央有一根泵轴自上而下通往混合室底部，泵轴连接泵轮的顶部，泵轮工作时叶轮上部和下部跟着泵轴一起旋转。泵轮的进液口位于泵轮的底部，叶轮进液口距离混合室底部有一段距离，在泵轮旋转时，通过进液口抽吸外部液体的同时能够产生内循环，而内循环已被证实对混合作用有极大提升。

2.2.2 计算域网格划分

选用有限元分析软件ANSYS中的Fluent模块对上述问题进行数值求解。首先对几何体进行网格划分。混合室及叶轮的结构都很复杂，这里选用适应性较好的四面体网格划分几何模型。混合室与叶轮接触面局部加密，以保证Fluent中的Interface数据准确传输，提高计算精度。由于模型计算数据的量很大，在现有硬件条件基础上，需要选择满足计算精度要求的网格数量尽量小的网格，以加快计算过程。网格无关性检查之后，确定网格尺寸和网格数。混合室网格最大尺寸4 mm，泵轮区网格最大尺寸为1 mm，模型网格数总计约150万，这一网格数量可以使模拟精度足够高。

2.3 计算条件

计算所关注的是混合澄清槽稳定运行之后的泵轮性能，所以采用稳态模拟进行计算。混合室和泵轮需设置为2个不同的求解域，混合室为静止求解域，泵轮为旋转求解域。两个求解域之间设置适宜的边界条件，使之相互关联。两个计算域耦合采用Fluent中的“Interface”进行数据传递。对于混合室求解域，其底面需设置一个直径100 mm的入口，采用法向速度作为其边界条件，速度大小根据入口流量设置；其顶面设置为自由出流边界条件，压力为101.3 kPa。对于泵轮求解域，其整个区域都要设置为旋转域，转速为150～650 r/min。

对于方差的离散化，选用二阶向后欧拉差分格式，其精度比较高。采用SIMPLE算法求解压力速度耦合方程组。收敛准则关系到计算精确度，一般收敛残差达到10-5就可以达到一般使用的精度要求，因此计算精度确定为10-5。

3 结果与讨论

3.1 流场与压力分布

CFD模拟可以计算求解域内每个节点上的流场与压力分布。模拟的流场分布如图3所示，混合室内压力分布如图4所示。

3.1.1 混合室内的速度矢量分布

图3为模拟的流场分布。从流场的纵剖面(图3(a))看出，在泵轮区域附近存在明显的流体循环，流体从叶片出口流向混合室底部，沿底部向中心进入泵轮吸液口，从吸液口进入叶片间隙，在离心力作用下向外到达叶片出口，完成一个循环。这种循环是在泵轮旋转离心力作用下实现的，其流体经过泵轮内部，泵轮提供循环动力。这种循环对混合室的混合性能尤其重要。

图3 模拟的流场分布

3.1.2 混合室内压力分布

图4(a)为整个混合室的压力分布纵剖面。可以看出，在远离泵轮位置，压力分布基本是流体在重力作用下的静压力分布。流体在远离泵轮处的流速很小，对压力的影响很小；而在泵轮内部和附近，压力分布明显偏离静压力分布：这是离心力场对流动的影响造成的。

尽管泵轮内压力偏离静压力分布很小，但从图4(b)仍可看出其偏离情况。每个叶片入口处都有一个小范围的低压区，这是流动对压力的影响结果。泵轮中无叶片区域和吸液管内，压力从上向下逐渐增大，但明显低于周围压力，这形成了抽吸作用。

图4 混合室内压力分布

3.2 泵轮叶片形状优化

泵轮结构优化的目的是使其性能最佳。泵轮性能主要指标有2个，抽吸高度和总循环流量。抽吸高度反映泵轮的抽吸性能，只有达到一定的抽吸能力，混合澄清才能实现连续逆流操作。试验中，抽吸高度是指进料室液面低于混合室液面的高度。模拟中省略了进料室，因此抽吸高度要从混合室入口压力进行计算，公式为

(4)

式中：hm—混合室高度，mm；Pin—混合室入口压力，Pa；Patm—101.3 kPa；ρ—流体密度，kg/L；g—重力加速度，m/s2。

根据模拟计算的混合室入口压力可以计算抽吸高度。泵轮的总循环流量是指从泵轮吸液口进入泵轮的流体流量(或8个叶片间隙出口流量之和)，包括两部分：一部分是混合室入口流量；另一部分是3.1节提到的泵轮循环流量。循环流量反映泵轮的混合性能，循环流量越大，表明液体在泵轮区域内循环接触的次数越多，混合性能越好。

对比不同泵轮结构模拟结果可优化泵轮直径、厚度、吸入管长度、叶片出口倾角等参数。图5为模拟得到的15°、45°、90°不同叶片出口倾角下抽吸高度随泵轮转速的变化情况。根据模拟结果可计算循环总流量。图6为模拟得到的不同叶片出口倾角下的泵轮总循环流量随转速的变化情况。

图5 不同叶片出口倾角下抽吸高度随泵轮转速的变化

图6 不同叶片出口倾角下总循环流量随泵轮转速的变化

由图5看出：抽吸高度随泵轮转速提高而增大；3种不同叶片出口倾角的泵轮的抽吸高度差别不大。

由图6看出，当叶片出口倾角为45°时，泵轮总循环流量最大；而90°时，总循环流量最小。以泵轮总循环流量为优化目标，则叶片出口倾角为45°的泵轮最佳。

3.3 混合室内的混合状况

图7为混合室和泵轮内的湍动能分布。图3表明，混合室内最大流速出现在其底部，表明混合室内的强混合区在泵轮内和其下方，而在其他区域混合强度很小。图7进一步验证了这个结果：湍动能在泵轮内外叶片两端的位置为最大，表明液滴主要在这2个位置发生破碎。

图7 混合室和泵轮内的湍动能分布

泵轮混合作用主要发生在泵轮及其下部的一个较小的范围内，而其上部速度很小，这说明混合室高度不应该设计太高。如果搅拌强度不够，可以在泵轮上方增加叶片来加强。

3.4 模拟结果与实测结果对比

为了验证模拟结果的可靠性，将模拟得到的抽吸高度与实测的抽吸高度进行对比，结果如图8所示。

图8 抽吸高度模拟值与实测值的对比

由图8看出：模拟结果比实测结果稍大一些。原因可能是模拟过程中忽略了叶片厚度，采用无厚度的“薄壁面”代替叶片，可使泵轮叶片间隙大于实际叶片间隙，相当于在一定程度上增大了泵轮直径。

这种偏差是规律性的，可以校正去除。为此，将模拟抽吸高度与实测抽吸高度之间的差值与泵轮转速进行关联，得到如下矫正公式：

hexp=hsim-0.092 4ω。

(5)

式中：hexp—实测抽吸高度，mm；hsim—模拟抽吸高度，mm；ω—搅拌速度，r/min。

根据式(5)计算得到的矫正后的模拟结果与实测结果吻合很好，这也证明了模拟结果的可靠性，说明CFD模拟可以用作混合澄清槽结构优化和实际操作指导的一种辅助手段。

4 结论

利用有限元分析软件ANSYS中的Fluent模块模拟泵轮式混合澄清槽混合室内CFD状况，得到以下结论：

1)混合室泵轮区域及附近存在较大的流体循环，即流体从泵轮叶片甩出后，再次由泵轮吸液口进入泵轮，从而有利于混合；

2)由于离心力对流体流动的影响，在泵轮中心区域和吸液管内，其压力明显低于周围混合室压力，从而形成泵轮的抽吸作用；

3)叶片出口倾角为45°时，泵轮性能最佳，在抽吸高度相当情况下，泵轮总循环流量最大；

4)混合室内的强混合区集中在泵轮内和其下方，湍动能在泵轮叶片两端达到最大，说明液滴主要在这2个位置发生破碎；

5)泵轮抽吸高度模拟结果略大于实测结果，矫正后的模拟结果与实测结果吻合很好，表明模拟结果可靠。